不同失效模式下平面张弦梁结构受力全过程刚度变化

蒋友宝^{1, 2}，李耀¹，杨伟军¹

(1. 长沙理工大学 土木与建筑学院，湖南 长沙，410004；

2. 东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京，210096)

摘要：针对现有关于平面张弦梁结构受力全过程中刚度变化规律研究不够系统化的不足，采用理论推导、有限元分析和试验验证等策略对此问题进行深入分析。首先，运用一阶方法推导简化平面张弦梁结构模型在外荷载作用下的跨中竖向位移和杆件内力的计算公式。在此基础上，研究上弦抗弯刚度及上下弦轴向刚度比这2个参数对结构竖向整体刚度的影响规律。最后，分析多个平面张弦梁结构模型在受力全过程中的刚度下降程度。结果表明：当各参数在常用范围内取值时，上弦抗弯刚度对结构整体刚度的影响不大。该结构的多种承载破坏模式均具有脆性破坏的特征。

关键词：平面张弦梁；一阶方法；整体刚度；失效模式；荷载-位移曲线

中图分类号：TU391             文献标志码：A         文章编号：1672-7207(2013)07-3006-08

Stiffness changes in full loading process with different failure modes for plane beam string structure

JIANG Youbao^{1, 2}, LI Yao¹, YANG Weijun¹

(1. School of Civil Engineering and Architecture, Changsha University of Science and Technology,

Changsha 410004, China;

2. Key Laboratory of Concrete and Pre-stressed Concrete structure of Ministry of Education,

Southeast University, Nanjing 210096, China)

Abstract: To solve the problem that the current research lacks systematizations on the law of stiffness changes of plane beam string structure in full loading process, intensive study was performed with the strategies of analytical deduction, finite element analysis and experimental validation. Firstly, based on the first order analysis method, the calculating formulas of mid-span vertical displacement and member internal force were obtained for a simplified plane beam string structure model. Then, the effects were studied on the global stiffness with different bending stiffness of upper chord and axial stiffness ratio of upper chord to lower chord. Finally, the reducing degree of global stiffness was analyzed in full loading process for different plane beam string structures. The results indicate that the bending stiffness of upper chord influences the global stiffness little when each parameter adopts common values. The failure modes hold the brittle characteristics for plane beam string structure.

Key words: plane beam string structure; first order method; global stiffness; failure modes; load-displacement curve

张弦梁结构是近年发展起来的大跨度钢结构形式之一。Saitoh等^[1-2]最先对该结构受力基本原理进行了深入研究。随后，苏旭霖等^[3]采用瑞利-里兹法推导了圆弧线型张弦梁结构在荷载态与张拉状态下的变形与内力计算公式，模型张拉与加载试验结果表明该公式具有较好的精度。Wu^[4]推导了张弦梁结构中撑杆屈曲荷载的计算公式，并分析了不同参数下撑杆的稳定性能。吴祖咸等^[5]采用有限元分析技术对该结构的受力性能进行了较详尽的参数分析，明确了各参数对结构受力的影响规律。此外，赵宪忠等^[6]对该结构张拉时的结构性能进行了正交试验研究；李刚等^[7]提出了等代张拉刚度的概念，并给出了实际工程中张拉成型控制方式的选取建议。这些对结构力学性能的研究为该结构应用于工程实践提供了较好的技术参考。但它们主要针对整体刚度按受荷初始阶段考虑的情形以及整体刚度随施工张拉过程而逐步形成的情形。在对该结构受荷全过程中力学性能的研究方面，目前也已有一些进展。李秀敏等^[8]结合一榀10 m跨索支承实腹式预应力钢拱模型试验进行了受力全过程研究，表明索支承钢拱结构的承载性能较为优越；张勇等^[9]分析了多种因素对平面张弦梁结构受力性能的影响，认为初始几何缺陷对承载力影响不大；蒋友宝等^[10]采用非线性有限元技术对该结构的受力全过程进行了参数分析。但是，上述研究^[8-10]在平面张弦梁结构承载全过程中整体刚度的变化规律方面仍不够系统化，如没有给出不同失效模式下整体刚度在全过程中的变化规律。基于此，本文作者采用一阶分析方法较全面地研究了张弦梁结构整体刚度的构成规律，然后对一榀简化的张弦梁模型与一榀实际工程中的张弦桁架模型进行了受力分析，得到了它们承载过程中整体刚度的变化特性。

1  基于一阶方法的受力分析

张弦梁结构的整体刚度一般较大，且整体呈弯曲受力，因而受力过程中几何非线性效应并不突出^[11]。为此，对于简单的张弦梁结构，采用一阶方法来进行受力分析是可行的。

1.1  计算模型与假定

设有一榀跨度为l的张弦梁结构，上弦和下弦的线型均为圆弧曲线，对应的矢跨比和垂跨比均为1/20，其尺寸和撑杆布置情况见图1所示。其中，X₁为中间撑杆内力；F为轴力；M为弯矩。

在利用一阶方法求解时，假定上弦的剪切效应和撑杆的轴向变形不大，可以忽略；同时下弦钢索为理想柔性，不能受压，也不能受弯。由于张弦梁结构具有一次超静定，因此可利用一阶方法来求得跨中位移和杆件内力。

图1  平面张弦梁结构计算模型

Fig.1  Calculation model for plane beam string structure

1.2  结构位移与内力计算

若假定钢索和钢材的弹性模量分别为E₁和E，上弦和下弦的面积分别为A₂和A₁ ，上弦的惯性矩为I；则下弦的轴向刚度为E₁A₁，上弦的轴向刚度和抗弯刚度分别为EA₂和EI。

根据张弦梁结构破坏模式的特点，在研究其全过程受力性能时需要考虑上弦节点2处塑性铰出现前和出现后的2种情形。

对于节点2处塑性铰出现前的情形，由力学基本方程可求得中间撑杆内力X₁的计算公式为

      (1)

则节点2的竖向位移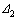为

           (2)

当节点2处塑性铰出现后为静定结构，根据静定结构的位移计算方法，可得2点竖向位移为

     (3)

结构的整体刚度可计算为

                (4)

因而将式(2)和(3)代入后便可得到2种情形下结构整体刚度的具体计算式。它们均为各种参数的复杂函数，可记为。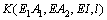

对于节点2处塑性铰出现前的情形，在求得多余力X₁后，结构已变成静定结构；而节点2处塑性铰出现后该结构也变静定结构，因此，它们的内力均可通过求解静力平衡方程得到。在各种情形下计算得到的内力如表1所示。由于对称性，只考虑了一半结构的内力。

表1  各种状态下结构杆件的内力表达式

Table 1  Internal forces of members under all states

在推导位移和内力解析计算公式时并没有考虑预应力的影响。原因在于本文的目的主要是利用这些公式来研究张弦梁结构使用阶段的整体刚度和承载性能，而预应力对这2方面的影响并不大^[10]。

2  整体刚度的参数分析

利用已得到的解析计算公式可对含有柔性索和刚性上弦的张弦梁结构受力全过程中整体刚度的变化规律进行参数分析。

2.1  参数的选取和公式验证

选取2个参数和β，其计算公式分别为

               (5)

                (6)

它们代表了上弦抗弯刚度、轴向刚度分别与下弦轴向刚度的匹配程度，表2所示为已建张弦梁工程中的α和β取值。可见，表2中的值与文献[1]的建议取值范围(10^-4~10^-3)较为吻合。

为方便分析，假定有一标准模型，其中，l=10 m，I=19 976 192 mm⁴，A₁=500 mm²，E₁=E=2×10⁵ MPa，A₂=4 928 mm²，F=1×10⁴ N。此标准模型中= 4×10^-4，β=9.86，它们均在常用的范围内。因而该标准模型具有一定的代表性。

对此标准模型，在ANSYS程序中，按节点2处不出现塑性铰考虑，中点挠度约为10.48 mm；按节点2处出现塑性铰考虑，中点挠度约为14.07 mm。若将上述参数代入式(2)和(3)，经计算可得节点2的位移分别为10.63 mm和14.12 mm。可见，计算值与模拟值吻合程度较好，上述位移解析计算公式具有较高精度。

表2  已建张弦梁工程的结构参数

Table 2  Structural parameters of existing projects

2.2  上弦抗弯刚度的影响

假定在标准模型中仅变化上弦抗弯刚度，则不同下整体刚度的变化如图2所示。

从图2可知：当由10^-4提高至10^-3时，节点2处塑性铰出现后整体刚度较塑性铰出现前的下降程度由20%增大为40%。这说明在下弦轴向刚度一定时，上弦抗弯刚度越大，塑性铰出现后，结构整体刚度的下降程度就越大。

图2  上弦抗弯刚度对竖向整体刚度的影响

Fig.2  Effects of bending stiffness of upper chord on vertical global stiffness

从图2还可知，按节点2处塑性铰出现前考虑，当由10^-4提高至10^-3时(即增大10倍)，结构整体刚度仅提高了22%左右，提升程度不大。而节点2处塑性铰出现后，当由10^-4提高至10^-3时，结构整体刚度仅提高了2%左右，提升程度更小。可见，无论节点2处是否出现塑性铰，增大上弦抗弯刚度对该结构整体刚度的改善作用都不大，这表明张弦梁结构的整体刚度主要是由上弦和下弦按桁架受力形成的刚度来提供的。

2.3  轴向刚度比的影响

在承载过程中，下弦索屈服后会进入塑性阶段，弹性模量会减小，这导致结构整体刚度会下降。

钢索一般由高强钢丝、钢绞线集合而成。实测的常温下高强钢丝的典型应力应变曲线^[18]如图3(a)所示。可见，其极限伸长率一般不低于4%。但对于集合而成的钢索，由于钢丝受力的不均匀性，其伸长率一般要小得多，一般仅为2%左右。参照文献[19]，此处假定钢索应力应变曲线可用三折线模型来表示，见图3(b)。假定索材料参数取值按表3中数据确定，其中k表示索屈服后弹性模量的下降程度，即屈服后弹性模量为E₁/k。

图3  钢丝和钢索的应力-应变关系曲线

Fig.3  Curves of stress-strain for wire and cable

表3  简化的索材料参数

Table 3  Simplified material parameters of cable

若下弦屈服之前轴向刚度比为β，则屈服后轴向刚度比将变为kβ(因索垂跨比一般不大，可近似按下弦各索段拉力相等考虑)。定义此时整体刚度的下降程度r计算式为

             (7)

假定上、下弦截面面积之和不变，而两者的比值发生变化，其他参数仍同标准模型一致。考虑节点2处不出现塑性铰的情形，则整体刚度变化如表4所示。

表4  上下弦轴向刚度比对竖向整体刚度的影响

Table 4  Effects of axial stiffness ratio of upper chord to lower chord on vertical global stiffness

由表4可知，在上、下弦截面面积之和一定时，索屈服后结构整体刚度的下降程度为51%~64%。

3  不同失效模式下的刚度变化特征

在实际工程中，张弦梁结构在平面外一般有侧向支撑，因此其平面外的整体稳定性能通常可得到保证。为此，以下分析失效模式时仅考虑了平面内的结构整体承载性能与平面外的上弦稳定性能。

3.1  上弦破坏模式

上弦破坏的计算模式分为2种：一是强度破坏；二是失稳破坏(包括平面内失稳与平面外失稳)。由于失稳破坏具有突然性，因此一旦上弦某一区段发生失稳，即可认为上弦已破坏；而对于前者，由于张弦梁结构具有一次超静定，因此某一截面强度破坏后，整个上弦尚不至于立即破坏，需等下一截面强度破坏时，整个上弦才达到破坏状态。

假定结构布置如图1所示，且每个撑杆处在平面外均设有侧向支撑。设上弦采用Q235焊接工字钢，截面尺寸(高度×宽度×腹板厚度×翼缘厚度)为160 mm×200 mm×6 mm×8 mm，屈服应力为235 MPa。该截面参数参考了文献[8]中的试验模型。下弦索的面积仍取为A₁=500 mm²。

在张弦梁结构模型中2点处内力最大，当按强度破坏而出现塑性铰时，压弯构件强度计算公式^[20]为

≤f               (8)

其中，N和M_x分别为截面轴压力和弯矩；A_n为净截面积；和分别为截面塑性发展系数和净截面模量；f为钢材屈服强度。可知，当F=92.1 kN，2点将出现塑性铰。在出铰后，结构整体刚度下降了约26%，若节点3截面再出现塑性铰，则可继续加载至F=129.5 kN。整个过程中荷载位移曲线将近似如图4所示。

图4  上弦强度破坏模式对应的荷载-位移曲线

Fig.4  Curves of load-displacement for strength failure mode of upper chord

当23区段发生平面内失稳破坏时，根据钢结构设计规范^[20]，平面内失稳计算公式

≤f          (9)

其中，和分别为弯矩作用平面内的轴心受压构件稳定系数和对较大受压纤维的毛截面模量；为等效弯矩系数；为欧拉临界力除以1.1。可知，当F=90.7 kN时，上弦即宣告失效。显然，整个过程中结构刚度的下降程度将不明显。

当23区段发生平面外失稳破坏时，根据钢结构设计规范^[20]，平面外失稳计算公式

≤f             (10)

其中，为弯矩作用平面外的轴心受压构件稳定系数；为均匀弯曲受弯构件的整体稳定系数；为截面影响系数；为等效弯矩系数。可知，当F=88.6 kN时，上弦即宣告失效。整个过程中结构刚度的下降程度同样也不明显。

3.2  下弦拉索破坏模式

假定拱强于索较多，则结构的破坏模式将表现为下弦的受拉破坏。

例如，设此时上弦的截面不变，而下弦索的面积调整为A₁=150 mm²，则根据下弦索的内力变化规律和图3(b)简化的钢索本构模型，计算可知，在F=60.1 kN时，拉力最大的索段达到屈服。此时，结构整体刚度下降了约55%，然后，继续加载至77.3 kN时，该索段达到极限强度，因而，整个受力过程中荷载-位移曲线如图5所示。

图5  下弦破坏模式对应的荷载-位移曲线

Fig.5  Curves of load-displacement for cable failure mode

3.3  刚度变化模式

已完成承载破坏的张弦梁结构模型试验^{[8, 16]}如表5所示。可见，这些试验荷载位移曲线中整体刚度下降的程度都不大。这与本文失效模式分析结果较为吻合。

根据以上试验结果和本文计算结果可知，整个受力过程中张弦梁结构刚度的下降程度并不大，没有出现如钢筋混凝土适筋梁荷载位移曲线中的屈服阶段，因而张弦梁结构承载破坏模式具有脆性破坏的特征。但下弦拉索破坏模式中，刚度下降程度要较上弦破坏模式稍大。

4  工程实例验证分析

以上在分析不同失效模式下平面张弦梁结构刚度变化特征时主要是针对上弦为实腹式截面情形。在实际工程中上弦还有采用格构式截面(桁架)情形。为此，选用一张弦桁架模型(尺寸参数参考了哈尔滨国际会展中心张弦桁架)来对上述结论进行进一步验证。

4.1  张弦桁架模型

该张弦桁架模型跨度L=128 m，假定其面外有足够的支撑。承重索截面面积16 895 mm²，弹性模量E=1.95×10⁵ N/mm²；拱架上、下弦杆的外径×厚度分别为480 mm×18 mm和480 mm×12 mm，横杆和立面斜腹杆的外径×厚度为168 mm×6 mm，水平斜腹杆的外径×厚度为273 mm×7 mm，支座附近杆件截面适当加强，撑杆采用圆形钢管，截面积为7 961 mm²，间距9.2 m，弹性模量E=2.0×10⁵ N/mm²。索的垂跨比为0.03，拱的矢跨比为0.08。拉索的初始预应力取为200 MPa，承受全跨荷载g，钢材为理想弹塑性，f_y=345 MPa。计算模型如图6所示。

表5  已完成承载破坏的平面张弦梁结构试验模型

Table 5  Existing experimental model for plane beam string structure with load bearing failure

图6  张弦桁架模型及截面布置(单位：mm)

Fig.6  Truss string structure and its section configuration

4.2  有限元分析结果

分析表明，此结构中下弦索的安全储备较上弦拱架高一些，因而其破坏模式为上弦拱架的平面内承载破坏，索的材料非线性可不考虑。

在ANSYS软件中，采用beam188单元模拟各桁架杆件，link10单元模拟下弦索，link8单元模拟撑杆，从而建立其有限元分析模型。为提高分析精度，同时考虑几何非线性和材料非线性(上弦桁架)的影响。计算表明：当全跨荷载g约为140 kN/m时，在中部较长区域内拱架的2根上弦杆均已屈服(应力达到345 MPa)，如图7所示，此时上弦桁架已达到其平面内承载极限状态。

取跨中上弦桁架节点的竖向位移作为代表值(向下为正)，则全过程荷载-位移曲线如图8所示。可见，整个受力过程中该张弦桁架的刚度变化不大，仍然具有脆性破坏的特征。

图7  张弦桁架结构对应的破坏模式

Fig.7  Failure mode for truss string structure

图8  张弦桁架结构对应的荷载-位移曲线

Fig.8  Curves of load-displacement for truss string structure

5  结论

(1) 当平面张弦梁结构的高跨比和参数分别在1/11~1/8和10^-4~10^-3范围内取值时，上弦抗弯刚度对结构整体刚度的贡献不大。

(2) 在分析的破坏模式范围内，平面张弦梁结构整个受力过程中刚度下降的程度不大，荷载-位移曲线无屈服阶段，因而其承载破坏模式具有脆性破坏的特征。

参考文献：

[1] Saitoh M, Kuroki F. Structural planning of beam string structure[C]// Proceedings of the International Colloquium on Space Structures for Sports Buildings. Beijing: Science Press, 1987: 120-127.

[2] Saitoh M, Okada A. The role of string in hybrid string structure[J]. Engineering Structures, 1999, 21(8): 756-769.

[3] 苏旭霖, 刘晟, 薛伟辰. 基于瑞利-里兹法的预应力张弦梁变形与内力分析[J]. 空间结构, 2009, 15(1): 49-54, 96.

SU Xulin, LIU Sheng, XUE Weichen. Deformation and internal force analysis of prestressed beam string structure based on Rayleigh-Ritz method[J]. Spatial Structures, 2009, 15(1): 49-54, 96.

[4] WU Minger. Analytical method for the lateral buckling of the struts in beam string structures[J]. Engineering Structures, 2008, 21(8): 2301-2310.

[5] 吴祖咸, 楼文娟, 高子珺. 单向张弦梁结构的受力性能研究[J]. 钢结构, 2010, 25(7): 1-3, 18.

WU Zuxian, LOU Wenjuan, GAO Zijun. Mechanics behavior research on beam string structure[J]. Steel Construction, 2010, 25(7): 1-3, 18.

[6] 赵宪忠, 陈建兴, 陈以一. 张弦梁结构张拉过程中的结构性能试验研究[J]. 建筑结构学报, 2007, 28(4): 1-7, 50.

ZHAO Xianzhong, CHEN Jianxing, CHEN Yiyi. Experimental study on structural performance during prestressing of beam string structure[J]. Journal of Building Structures, 2007, 28(4): 1-7, 50.

[7] 李刚, 冯大斌, 梁存之. 张弦梁张拉成型控制方式研究[J]. 施工技术, 2010, 39(8): 170-172.

LI Gang，FENG Dabin，LIANG Cunzhi. Study on shape forming processing control of beam string structures[J]. Construction Technology, 2010, 39(8): 170-172.

[8] 李秀敏, 石永久, 王元清. 索支承实腹式钢拱结构承载性能的试验研究[J]. 空间结构, 2005, 11(3): 27-32.

LI Xiumin, SHI Yongjiu, WANG Yuanqing. Experimental investigation on cable-strut arch structures[J]. Spatial Structures, 2005, 11(3): 27-32.

[9] 张勇, 田向阳, 王元清, 等. 张弦梁结构弹塑性大位移分析[J]. 北京交通大学学报, 2005, 29(4): 19-24.

ZHANG Yong, TIAN Xiangyang, WANG Yuanqing, et al. Elasto-plastic large displacement analyses of beam string structure[J]. Journal of Beijing Jiao Tong University, 2005, 29(4): 19-24.

[10] 蒋友宝, 冯健, 蒋剑锋, 等. 张弦梁结构若干参数对承载性能的影响分析[J]. 工业建筑, 2008, 38(1): 103-105.

JIANG Youbao, FENG Jian, JIANG Jianfeng, et al. Effects of some parameters on mechanical performance of the beam string structures[J]. Industrial Construction, 2008, 38(1): 103-105.

[11] 杨叔庸, 孙文波, 舒宣武. 126.6 m跨张弦桁架结构的设计与研究[J]. 空间结构, 2005, 11(1): 24-29.

YANG Shuyong, SUN Wenbo, SHU Xuanwu. Design and research of a truss string structure with a long span of 126.6 m[J]. Spatial Structures, 2005, 11(1): 24-29.

[12] 陈以一, 沈祖炎, 赵宪忠, 等. 上海浦东国际机场候机楼R2钢屋架足尺试验研究[J]. 建筑结构学报, 1999, 20(2): 9-17.

CHEN Yiyi, SHEN Zuyan, ZHAO Xianzhong, et al. Experimental study on a full-scale roof truss of Shanghai Pudong International Airport Terminal[J]. Journal of Building Structures, 1999, 20(2): 9-17.

[13] CHEN Fubin, LI Qiusheng, WU Jiurong, et al. Wind effects on a long-span beam string roof structure: Wind tunnel test, field measurement and numerical analysis[J]. Journal of Constructional Steel Research, 2011, 67(10): 1591-1604.

[14] 范峰, 支旭东, 沈世钊. 哈尔滨国际会议展览体育中心主馆屋盖钢结构设计[J]. 建筑结构, 2008, 38(2): 1-4.

FAN Feng, ZHI Xudong, SHEN Shizhao. Design of string structures in Harbin International Conference Exhibition and Sports Center[J]. Building Structure, 2008, 38(2): 1-4.

[15] 黄明鑫, 钱卫军, 黄开龙, 等. 哈尔滨国际会展体育中心大跨张弦桁架结构的安装技术[J]. 工业建筑, 2007, 37(9): 41-44.

HUANG Mingxin, QIAN Weijun, HUANG Kailong, et al. Erection technology of large span chord-tension truss structure for Harbin International Exhibition Center[J]. Industrial Construction, 2007, 37(9): 41-44.

[16] 薛伟辰, 刘晟, 苏旭霖, 等. 上海源深体育馆预应力张弦梁优化设计与试验研究[J]. 建筑结构学报, 2008, 29(1): 16-23.

XUE Weichen, LIU Sheng, SU Xuling, et al. Design optimization and experimental study on prestressed beam string of Shanghai Yuanshen Arena[J]. Journal of Building Structures, 2008, 29(1): 16-23.

[17] XUE Weichen, LIU Sheng. Studies on a large-span beam string pipeline crossing[J]. Journal of Structural Engineering, 2008, 134(10): 1657-1667.

[18] 张昊宇, 郑文忠. 高温下1770级Φ^P5钢丝蠕变及应力松弛性能试验研究[J]. 土木工程学报, 2006, 39(8): 7-13.

ZHANG Haoyu, ZHENG Wenzhong. An experimental study on the creep and stress relaxation properties of 1770-Φ^P5 prestressing steel wires at high temperature[J]. China Civil Engineering Journal, 2006, 39(8): 7-13.

[19] 蒋友宝, 郑晶, 李江, 等. 索材料非线性对平面张弦梁结构载性能的影响分析[J]. 工程建设, 2011, 43(3): 8-10, 35.

JIANG Youbao, ZHENG Jing, LI Jiang, et al. Influence analysis of material nonlinearity of cable on bearing capacity of plane beam string structure[J]. Engineering Construction, 2011, 43(3): 8-10, 35.

[20] GB 50017—2003, 钢结构设计规范[S].

GB 50017—2003, Code for design of steel structures[S].

(编辑  赵俊)

收稿日期：2012-06-19；修回日期：2012-09-26

基金项目：国家自然科学基金资助项目(11102029)；东南大学混凝土及预应力混凝土结构教育部重点实验室开放课题资助项目(02-2011)

通信作者：蒋友宝(1982-)，男，湖南永州人，博士，副教授，从事复杂结构分析与可靠度研究；电话：13755198993；E-mail: jiangybseu@163.com