
Evolutionary artificial neural network approach for predicting properties of Cu-15Ni-8Sn-0.4Si alloy
FANG Shan-feng(方善锋), WANG Ming-pu(汪明朴), WANG Yan-hui(王艳辉),
QI Wei-hong(齐卫宏), LI Zhou(李 周)
School of Materials Science and Engineering, Central South University, Changsha 410083, China
Received 17 October 2007; accepted 29 April 2008
Abstract: A novel data mining approach, based on artificial neural network(ANN) using differential evolution(DE) training algorithm, was proposed to model the non-linear relationship between parameters of aging processes and mechanical and electrical properties of Cu-15Ni-8Sn-0.4Si alloy. In order to improve predictive accuracy of ANN model, the leave-one-out-cross-validation (LOOCV) technique was adopted to automatically determine the optimal number of neurons of the hidden layer. The forecasting performance of the proposed global optimization algorithm was compared with that of local optimization algorithm. The present calculated results are consistent with the experimental values, which suggests that the proposed evolutionary artificial neural network algorithm is feasible and efficient. Moreover, the experimental results illustrate that the DE training algorithm combined with gradient-based training algorithm achieves better convergence performance and the lowest forecasting errors and is therefore considered to be a promising alternative method to forecast the hardness and electrical conductivity of Cu-15Ni-8Sn-0.4Si alloy.
Key words: Cu-15Ni-8Sn-0.4Si alloy; electrical property; aging process; artificial neural network; differential evolution; leave-one- out-cross-validation
1 Introduction
Cu-15Ni-8Sn alloys have been widely used in the electronic industry for bushings, bearings, springs, and electronic connectors[1-3]. They combine excellent age hardenability and formability with good stress relaxation, electrical conductivity and corrosion resistance. Because of low price, outstanding properties and being harmless to health, Cu-15Ni-8Sn alloys have been considered as substitutes for Cu-Be alloys. Many studies have been done on the age hardening in these alloys for a long time [4-8]. How to improve the overall properties of these alloys has been the subject of a number of studies[9-12]. Up to now, the process optimization of these alloys has been mainly studied empirically by trial-and-error methods, which are expensive and time-consuming. Therefore, simulation of the effects of aging treatment processes by numeric methods to obtain optimal properties of these alloys is very important.
With the development of computer science, a kind of data mining and artificial intelligence technique such as the artificial neural network(ANN) has been used in the fields of processing and design of copper alloys [13-14]. ANN is a non-linear statistical analysis technique and especially suitable to simulate systems, which are hard to be described by physical models. Since the development of the back-propagation method, many algorithms have been proposed and used to train neural networks, such as modified back-propagation, back- propagation using the conjugate-gradient approach, scaled conjugate-gradient (SCG), and Levenberg–Marquadt algorithm(LM). However, these training algorithms only based on gradient information usually converge to local minima. The global optimization algorithms, such as genetic algorithm(GA) and simulated annealing(SA), may be useful to avoid such a local minima problem. In fact, there is no single training algorithm that has the best performance compared with all other methods on all problem domains. One feasible solution method is to use the global optimization algorithms combined with gradient information methods to train the neural network to achieve acceptable solution.
Differential evolution(DE) is one of the recent population-based global optimization techniques[15-16]. DE corresponds to an improved version of GA. However, the principle difference between them consists of the mutation operation. DE is significantly fast and robust at numerical optimization and is more likely to find a true global optimum of function. The aim of this work is to investigate the use of ANN based on DE training algorithm(DEANN) and compare DEANN with different type of training algorithms. Furthermore, in this study, it is focused on using the novel neural network-based method to forecast the hardness and electrical conductivity of Cu-15Ni-8Sn-0.4Si alloy.
2 DE training algorithm
DE is a heuristic method for minimizing nonlinear and non-differentiable continuous space functions, so it can be applied to global searches within the weight space of a typical neural network. The most popular neural network model is the so-called back-propagation neural network(BPN). Training a BPN is typically realized by adopting an error correction strategy that adjusts the network weights through minimization of learning error:
E=gED+(1-g)EW (1)
where EW is the mean value of the sum squares for the network parameters, ED is the mean value of the sum error squares between the real output and the target output, and g is the performance ratio. The optimization goal is to minimize the objective function E by optimizing the values of the network weights: W=(w1, w2, …, wD).
DE can be briefly described as follows.
1) Initialization operation: generate the initial individuals  where i (i=1, 2, …, Np) is the index to the population and G (G=1, 2, …, Gmax) is the generation to which the population belongs; determine the mutation probability F, the crossover probability CR, and the maximal number of generations Gmax; set the current generation G=0.
where i (i=1, 2, …, Np) is the index to the population and G (G=1, 2, …, Gmax) is the generation to which the population belongs; determine the mutation probability F, the crossover probability CR, and the maximal number of generations Gmax; set the current generation G=0.
2) For each individual  do steps 3-5 to produce the population for the next generation G+1.
do steps 3-5 to produce the population for the next generation G+1.
3) Mutation operation: a perturbed individual 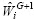 is generated as follows:
is generated as follows:

where j, k, b∈[1, Np], integer and mutually different. The integer j and k are chosen randomly from the interval [1, Np] and are different from the running index i.  is the best individual of the current generation. F is a real constant factor within [0, 2], which controls the amplification of the differential variation
is the best individual of the current generation. F is a real constant factor within [0, 2], which controls the amplification of the differential variation 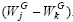
4) Crossover operation: the perturbed individual  and the current individual
and the current individual  are selected by a binomial distribution to perform the crossover operation to generate the offspring
are selected by a binomial distribution to perform the crossover operation to generate the offspring  namely,
namely,

where Rk is a random number within [0, 1].
5) Evaluation operation: the offspring 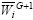 competes with its counterpart parent
competes with its counterpart parent  in the current population. As a result, the vector with lower objective function value wins a place in the next generation population. The evaluation operation is expressed as
in the current population. As a result, the vector with lower objective function value wins a place in the next generation population. The evaluation operation is expressed as

6) G=G+1.
7) Repeat steps 2-7 until the number of generation G reaches the maximum number Gmax.
The minimum value of mean square learning error (E in Eqn.(1)) is expressed as Emin in the context of this study. The parameters of DE are chosen in accordance with the rules summarized by STORN and PRICE [15-16].
3 Modeling using ANN and DEANN
3.1 Model setting
For forecasting a multivariate regression problem, the inputs of ANN are ageing temperature and aging time, respectively. The outputs are the hardness and electrical conductivity of copper alloy. Thus, the mapping function can be described as
Y1, 2=F(X1, X2) (5)
where Y is the predicted hardness and electrical conductivity of copper alloy, X1 is the aging temperature and X2 is aging time. The algorithms by means of the integration of the ANN model and DE were written in MatLab 7.0.
3.2 Collecting experimental data
The data used herein have been published in Ref.[17]. Cu-15Ni-8Sn alloy (mass fraction, %) was prepared by melting the component metals in an intermediate frequency induction furnace. The ingot obtained was homogenized at 860 ℃ for 6 h, then hot rolled at 860-650 ℃, and subsequently cold rolled after solution at 800 ℃ for 1 h and shaped into a suitable form for the following measurements. The conductivity was measured by double bridge. The hardness was measured by model HMV-2T low load micro-Vickers hardness tester.
The performance of the neural network and DEANN model is still strongly dependent upon the homogeneity of the model errors and the uniformity of the data sets. To ensure reasonable distribution and enough information in the data set, the aging tem- peratures are 350, 400 and 450 ℃. The aging time is 0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 6.0 and 8.0 h.
3.3 Results and discussion
Before the ANN is trained, all the data in the database are scale standardized by the expressions as follows:
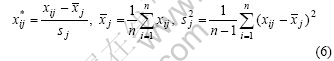
To evaluate the forecasting performance of the ANN model, some statistical metrics are used, such as root mean square error(RMSE), mean absolute percentage relative error(MAPE) and correlation coefficient(R). These metrics are calculated by the following equations:

where 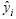 is the predicted value, yi is the measured value and n is the number of samples. RMSEP value means RMSE obtained by LOOCV technique for the test set in the context of this work.
is the predicted value, yi is the measured value and n is the number of samples. RMSEP value means RMSE obtained by LOOCV technique for the test set in the context of this work.
The BPN model with one hidden layer was used in this study. Firstly, LOOCV technique was applied to select the optimal number of hidden layer units. The optimal BPN structures are {2, 5, 2} for scaled conjugate gradient back-propagation(SCG) training algorithm and {2, 4, 2} for Levenberg-Marquardt back-propagation (LM) training algorithm, respectively. Performance comparison results for different training algorithms based on LOOCV technique are illustrated in Table 1. The correlation between the observed and calculated values by SCG training algorithm based on LOOCV technique is shown in Fig.1. It can be seen that the predicted values are in good agreement with the measured values of hardness and electrical conductivity, indicating that the correlation is quite good.
Table 1 Performance comparison results for different training algorithms based on LOOCV technique


Fig.1 Comparison of measured and predicted hardness and electrical conductivity by SCG training algorithm based on LOOCV technique (Symbols “○” denote experimental values of hardness and electrical conductivity[17]): (a) Hardness; (b) Electrical conductivity
Secondly, the efficiency of DE training algorithm for BPN was tested. In this experiment, we set F=0.8, CR=0.9. Furthermore, the performances of different neural networks training algorithms were compared. The performance was estimated through minimization of learning error at a restricted training iteration number. The maximal number of iteration is set to 10 000 for all training algorithms. Performance comparison results for different training methods are illustrated in Table 2 and Fig.2. As shown in Table 2 and Fig.2, the SCG training algorithm has a better forecasting performance than LM training algorithm. Although the LM training algorithm converges fastest, it leads to the highest forecasting errors. From all the experimental results, it is shown that the networks can achieve the best convergence performance and lowest forecasting errors if the DE training method combines with gradient information.
Table 2 Performance comparison results for different training methods

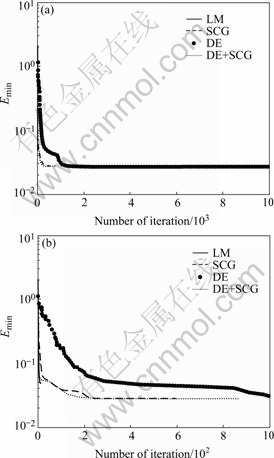
Fig.2 Performance comparison results with different training methods
Therefore, using both DE optimization and gradient information is a better alternative to that of the LM and SCG methods.
Once the BPN model is sufficiently trained, it can be used to predict new input data in the same knowledge domain. All the data from 350 to 450 ℃ and from 0 to 8 h are estimated. Fig.3 shows the predicted results for hardness and electrical conductivity of Cu-15Ni-8Sn- 0.4Si alloy as a function of aging time at different aging temperature. The predicted results are very close to the experimental values. The DE training algorithm combined with SCG training algorithm provides the lowest forecasting errors. It can be seen that the electrical conductivity increases gradually with the increases in aging time and aging temperature. The increase of the electrical conductivity is mainly due to the following factors[17-18]. Firstly, spinodal decomposition occurs in Cu-15Ni-8Sn-0.4Si alloy and it forms a modulated structure with Sn-rich zone and Sn-lean zone. Thus, the alloying agent is depleted and the probability of electron scattering is reduced. As a result, the electrical conductivity increases. Secondly, the dislocation produced by cold roll moves or restructures at the beginning of ageing so that the conductivity of the alloy increases very quickly. Subsequently, because 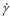 ((Cu,Ni)3Sn, coherent with matrix) and γ(Cu,Ni)3Sn, incoherent with matrix) phases precipitate in turn, the electrical conductivity of the alloy increases slowly. Lastly, the precipitation of Ni3Si phase during aging causes the alloying agent in the matrix to be depleted further. Therefore, the electrical conductivity of the alloy is higher than that of Cu-15Ni-8Sn alloy without Si.
((Cu,Ni)3Sn, coherent with matrix) and γ(Cu,Ni)3Sn, incoherent with matrix) phases precipitate in turn, the electrical conductivity of the alloy increases slowly. Lastly, the precipitation of Ni3Si phase during aging causes the alloying agent in the matrix to be depleted further. Therefore, the electrical conductivity of the alloy is higher than that of Cu-15Ni-8Sn alloy without Si.
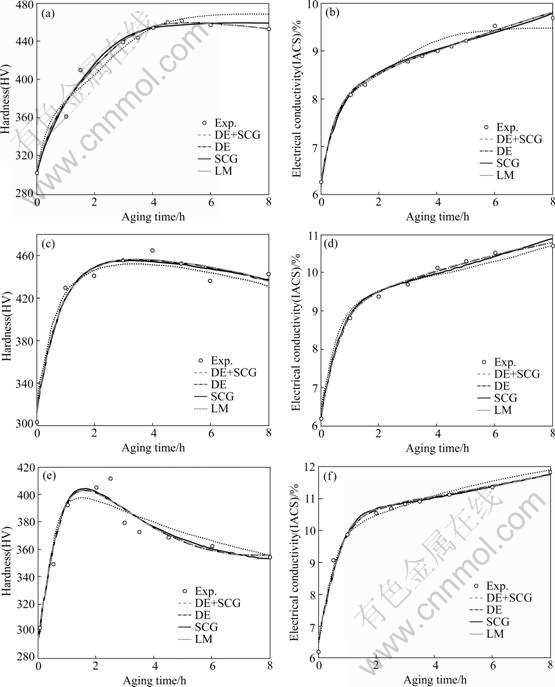
Fig.3 Predicted results for hardness and electrical conductivity as function of aging time at different aging temperatures (Symbols “○” denote experimental values of hardness and electrical conductivity[17]. Lines are predicted results of ANN model using different training algorithms): (a) Hardness after aging at 350 ℃; (b) Electrical conductivity after aging at 350℃; (c) Hardness after aging at 400 ℃; (d) Electrical conductivity after aging at 400 ℃; (e) Hardness after aging at 450 ℃; (f) Electrical conductivity after aging at 450 ℃
It can be seen from the hardness curves that at the aging treatment of 350 ℃, 5 h and 400 ℃, 4 h, the alloy can reach the maximal hardness (HV 460 or so[17]). The higher the aging temperature, the shorter the time of the peak hardness is reached. Although the time of the peak hardness is shorter, the peak hardness (HV 410 or so[17]) is lower after aging at 450 ℃ for 2.5 h. The peak value of calculated hardness at 450℃ is mainly attributed to the noise of the experimental data and the predicted error of the model. In short, the optimal aging temperature is 400 ℃ in this study. The increase of the hardness is mainly due to following reasons[17]. Firstly, the hardness is increased quickly because of the effect of spinodal hardening at the beginning of ageing. Spinodal decomposition forms fine modulated structure and creates coherent stress field periodically which hinders the movement of the dislocation. Secondly, the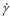 metastable phase that is converted from modulated structure is coherent with the matrix and thus its contribution to the strengthening effect is large. Lastly, the precipitation of Ni3Si phase during aging can produce additional strengthening effect on the hardness of the alloy. The decrease of the hardness after overaging is mainly due to the discontinuous precipitation of γ phase, which softens the alloy usually.
metastable phase that is converted from modulated structure is coherent with the matrix and thus its contribution to the strengthening effect is large. Lastly, the precipitation of Ni3Si phase during aging can produce additional strengthening effect on the hardness of the alloy. The decrease of the hardness after overaging is mainly due to the discontinuous precipitation of γ phase, which softens the alloy usually.
4 Conclusions
1) ANN model using different training algorithms based on LOOCV technique has been developed to forecast mechanical and electrical properties of Cu-15Ni-8Sn-0.4Si alloy. The predicted values are in good agreement with the measured values of hardness and electrical conductivity.
2) A novel approach based on artificial neural network(ANN) using differential evolution(DE) training algorithm has been applied to forecast the hardness and electrical conductivity of Cu-15Ni-8Sn-0.4Si alloy. The DE training algorithm combined with SCG training algorithm provides the lowest forecasting errors. Hence, this black-box model (DEANN+SCG) is very applicable for simulation of the aging process optimization of the alloy.
3) The maximal hardness (HV 460 or so[17]) is obtained after aging at 400 ℃ for 4 h. The increase of the hardness is mainly due to the effects of spinodal hardening, the precipitation of 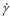 metastable phase and Ni3Si phase.
metastable phase and Ni3Si phase.
References
[1] SCHWARTZ L H, MAHAJAM S, PLEWES J T. Spinodal decomposition in a Cu-9Ni-6Sn alloy [J]. Acta Met, 1974, 22(5): 601-609.
[2] LASDAY S B. PM Cu-Ni-Sn strip alloys with particular response to aging develop favorable properties for electronic components [J]. Industrial Heating, 1991, 11: 26-30.
[3] SCOREY R, CHIN S, WHITE M J. Spinodal Cu-Ni-Sn alloys for electronic applications [J]. Journal of Metals 1984, 11: 52-54.
[4] WANG Yan-hui, WANG Ming-pu, HONG Bin. Microstructures of spinodal phases in Cu-15Ni-8Sn alloy [J]. Journal of University of Science and Technology Bejing, 2005, 12(3): 243-245.
[5] KIM C J, KONG M S, HAN S Z. Development of high strength Cu-Ni-Sn-(X) alloys [J]. J Jpn Copper Brass Res Association, 2000, 39: 157-160.
[6] SPOONER S, LEFEVRE B G. The effect of prior deformation on spinodal age hardening in Cu-15Ni-8Sn alloy [J]. Metall Trans, 1980, 11(7): 1085-1090.
[7] MIKI M, OGINO Y. Influence of solution treatment conditions on the cellular precipitation in Si-doped Cu-10Ni-8Sn alloy [J]. Materials Transactions JIM, 1991, 32(12): 1135-1140.
[8] ZHAO J C, NOTIS M R. Spinodal decomposition, ordering transformation, and discontinuous precipitation in a Cu-15Ni-8Sn alloy [J]. Acta Mater, 1998, 46(12): 4203-4218.
[9] MIKI M, OGINO Y. Effect of Si addition on the cellular precipitation in a Cu-10Ni-8Sn alloy [J]. Materials Transactions JIM, 1990, 31(11): 968-974.
[10] ZHENG She-lie, WU Jin-ming, ZENG Yue-wu. Ageing behavior of Cu-15Ni-8Sn alloy prepared by mechanical alloying [J]. Trans Nonferrous Met Soc China, 1999, 9(4): 707-711.
[11] ZENG Yue-wu. Influence of mechanical alloying on properties of Cu-15Ni-8Sn alloy [J]. The Chinese Journal of Nonferrous Metals, 2000, 10(4): 497-501. (in Chinese)
[12] SHI Hai-heng, WU Xing-fang, ZHANG Jing-guo. Investigation on age hardening of Cu-15Ni-8Sn alloy obtained by spray forming [J]. Heat Treatment of Metals, 2000(9): 6-8. (in Chinese)
[13] SU J H, LI H J, LIU P, DONG Q M, LI A J. Aging process optimization for a copper alloy considering hardness and electrical conductivity [J]. Computational Materials Science, 2007, 38: 697-701.
[14] LIU P, SU J H, DONG Q M, LI H J. Optimization of aging treatment in lead frame copper alloy by intelligent technique [J]. Materials Letters, 2005, 59: 3337-3342.
[15] STORN R, PRICE K. Differential evolution—A simple and efficient adaptive scheme for global optimization over continuous spaces [R]. TR-95-012, Berkeley, CA, USA: International Computer Science Institute, 1995.
[16] STORN P, PRICE K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces [J]. Journal of Global Optimization, 1997, 11(4): 341-359.
[17] WANG Yan-hui, WANG Ming-pu. Phase transformations of Cu-15Ni-8Sn-XSi and Cu-9Ni-2.5Sn-1.5A1-0.5Si alloys and their effects on the alloy’s properties [D]. Changsha: Central South University, 2004. (in Chinese)
[18] WANG Yan-hui, WANG Ming-pu, HONG Bin, LI Zhou, XU Gen-ying. Effect of Si addition on the microstructure and properties of Cu-15Ni-8Sn alloy [J]. Heat Treatment of Metals, 2003, 28(1): 41-44. (in Chinese)
Foundation item: Project(2002AA302505) supported by the Hi-tech Research and Development Program of China
Corresponding author: FANG Shan-feng; Tel: +86-731-8830264; E-mail: fang757@163.com
(Edited by LI Xiang-qun)