DOI: 10.11817/j.issn.1672-7207.2015.03.029
基于变形元件的节理岩体三轴压缩损伤本构模型
赵怡晴1,刘红岩2, 3,吕淑然4,邢闯锋2,张力民1, 5
(1. 北京科技大学 土木工程与环境学院,北京,100083;
2. 中国地质大学(北京) 工程技术学院,北京,100083;
3. 西藏大学 工学院,西藏 拉萨,850000;
4. 首都经济贸易大学 安全与环境工程学院,北京,100026;
5. 河北钢铁集团矿业有限公司,河北 唐山,063000)
摘要:基于岩体结构力学观点,将岩体看作是由岩块和结构面组成的复合体,分别采用基于统计损伤模型的弹性损伤变形元件和考虑结构面闭合及滑动的变形元件描述岩块和结构面在压缩荷载作用下的变形规律,进而建立相应的节理岩体压缩损伤本构模型。其次,针对上述损伤本构模型中最大拉应变破坏准则不适合于描述三向受力状态下岩石破坏的不足,基于Mises屈服准则推导出三向应力状态下的最大主应变与围压之间的关系,进而将该模型推广至三维情形。最后,通过算例对该模型的合理性进行验证。研究结果表明:该模型能够较好地反映围压对节理岩体试件强度及变形的影响规律,即随着围压增加,节理岩体试样峰值强度增加,而试样破坏时的最终应变减小。
关键词:围压;三轴压缩;宏观缺陷;微观缺陷;变形元件;损伤本构模型
中图分类号:TU452 文献标志码:A 文章编号:1672-7207(2015)03-0991-06
3-dimensional compression damage constitutive model of jointed rock mass based on deformation components
ZHAO Yiqing1, LIU Hongyan2, 3, L Shuran4, XING Chuangfeng2, ZHANG Limin1, 5
Shuran4, XING Chuangfeng2, ZHANG Limin1, 5
(1. School of Civil and Environmental Engineering, University of Science and Technology Beijing,
Beijing 100083, China;
2. College of Engineering & Technology, China University of Geosciences (Beijing), Beijing 100083, China;
3. School of Engineering, Tibet University, Lasha 850000, China;
4. School of Safety and Environment Engineering, Capital University of Economics and Business,
Beijing 100026, China;
5. Mining Co. Ltd. of Hebei Iron and Steel Group, Tangshan 063000, China)
Abstract: In accordance with the viewpoint of rock structure mechanics, rock mass was regarded as a compound of rock blocks and joints, and the deformation laws of rock block and joints under compression load were described with the elastic damage deformation component based on the statistical damage model and the joint closure and slippage deformation component, respectively. And the corresponding compression damage constitutive model of the jointed rock mass was established. Considering that the maximum tensile strain failure criterion adopted in above damage constitutive model is not suitable to describe the rock failure under three-dimensional stress conditions, the relationship between the maximum tensile strain and confining pressure under three-dimensional stress conditions was deduced based on Mises yield criterion, and this model was extended to three-dimensional conditions. A calculation example was adopted to preliminarily verify the validity of this model. The results show that the model can better reflect the effect law of confining pressure on jointed rock mass strength. Even though the jointed rock mass strength peak value increases with the augment of confining pressure, the final strain decreases when the jointed rock mass damages.
Key words: confining pressure; tri-axial compression; macroscopic defect; microscopic defect; deformation components; damage constitutive model
岩体是一种复杂的天然损伤地质体,其内部不仅包含着微裂隙、微孔洞等微观缺陷,而且包含节理、裂隙等宏观缺陷[1-3],这2类缺陷均对岩体在外力作用下的力学响应产生显著影响。Tang等[4-9]从微观、细观及宏观等角度研究了不同尺度缺陷对岩体力学特性的影响规律,得出了许多有意义的结论。但由于岩体本身结构复杂,导致现有研究成果仍与实际情况存在一定差别,其中一个重要原因就是对岩体内部微观缺陷考虑不足,如目前的岩体本构模型大都仅考虑节理等宏观缺陷的影响[10-12]。然而,节理岩体的破坏并非都是沿已有节理面产生,而可能发生在被节理面切割而成的岩石块体内部[13-15],而这种破坏形式正是微观缺陷发展、演化的结果。因此,如何更好地反映宏观和微观这2类不同尺度缺陷的共同影响是目前岩体本构模型研究中的重要课题。在这方面,Tang[16]进行了大量研究工作,将存在于岩体内的节理、裂隙看作是弹性模量极低的一种特殊介质,而将被节理切割而成的岩块看作是由众多强度服从随机分布的细观单元所组成的集合体,进而用连续介质力学方法处理非连续性问题,获得了良好效果。除此之外,目前很少见到有同时考虑宏观和微观缺陷对岩体力学特性影响的报道,为此,本文作者在基于孙广忠等[17]提出的岩体结构控制论的基础上,借鉴Maxwell模型的研究思路,综合考虑宏观和微观缺陷的共同影响,提出基于变形元件的节理岩体单轴压缩损伤本构模型。同时,根据Mises屈服破坏准则对上述损伤模型中的单轴拉应变破坏准则进行修正,进而将上述模型推广到三向受力状态,并利用该模型讨论围压对试件强度及变形的影响规律。
1 基于变形元件的岩体三轴压缩变形机制及本构方程
孙广忠等[17]以“岩体结构控制论”为基础认为岩体变形是岩体材料变形和岩体结构变形共同作用的结果,从而建立了较完整的岩体结构力学体系。很多学者也将岩石(体)看作是由弹性元件、塑性元件、黏性元件及摩擦元件等基本变形元件中的一种或多种按照不同组合方式形成的变形体,并根据相应的应力、应变关系得到多种不同的本构模型。如曹文贵等[18]采用黏性元件和非线性元件并联的方法模拟岩石的动态力学响应,从而建立了相应的本构模型。本文则借鉴Maxwell模型的研究思路并结合岩体在压应力作用下的变形特点,将岩体看作是由含天然微观损伤的岩块和节理面串联而成,如图1所示。
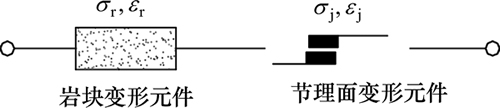
图1 节理岩体变形元件模型
Fig. 1 Deformation component model of jointed rock mass
若假设岩体的轴向应力、应变分别为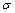 和
和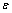 ,则按照图1所示的组合关系,有
,则按照图1所示的组合关系,有
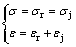 (1)
(1)
其中: 和
和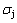 分别为岩块和节理的轴向应力;
分别为岩块和节理的轴向应力;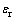 和
和 分别为岩块和节理的轴向应变。
分别为岩块和节理的轴向应变。
由式(1)可知,若能求出单轴压缩下岩块和节理面的轴向应变,则可得到岩体单轴压缩变形本构方程。下面分别对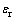 和
和 的计算方法进行讨论。
的计算方法进行讨论。
1.1 考虑微观缺陷的岩块变形本构方程
当将岩块看作是均质弹性材料时,其变形规律可用一种岩石力学元件——弹簧表示,采用胡克定理来描述,即
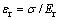 (2)
(2)
式中:Er为岩块弹性模量;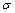 为应力。
为应力。
虽然弹性变形元件较简单,但无法反映岩石在压缩变形过程中表现出的宏观塑性特征。而Tang[16]认为岩石之所以在变形过程中出现塑性特征,是由于岩石是由众多强度不等的细观单元所组成,即使在较小的外力作用下也会有细观单元的破裂产生,进而在宏观上表现出塑性特征。目前研究认为组成岩石的微元强度服从统计分布规律[19],若假定微元强度服从Weibull分布,则根据最大拉应变破坏准则,其变形可表示为[16]
 (3)
(3)
其中:m和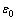 为拟合常数。在外力作用下岩块弹性模量将随微元的破坏而逐渐减小。
为拟合常数。在外力作用下岩块弹性模量将随微元的破坏而逐渐减小。
式(3)表示的是岩石在单轴应力状态下的力学特性,不适用于三向受力等复杂应力状态。首先,在该式中没有包含侧压力分量,其次,最大拉应变破坏准则也不适合于描述三向受力状态下的岩石破坏,因此,必须推导出三向状态下的最大主应变与围压之间的关系。假设岩石受到围压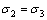 的作用,则最大主应变为
的作用,则最大主应变为
 (4)
(4)
式中: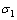 和
和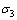 分别为第一、三主应力。
分别为第一、三主应力。
由于在三向应力状态下,试件的变形与破坏更具有明显的塑性特征,因此,选用Mises屈服准则作为微元体的破坏准则,即
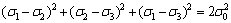 (5)
(5)
式中: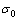 为岩石微元体单轴压缩强度,当
为岩石微元体单轴压缩强度,当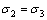 时,式(5)可变为
时,式(5)可变为
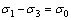 (6)
(6)
将式(6)代入(4)可得
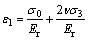 (7)
(7)
式中: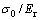 为微元体在单轴应力作用下的破坏应变,它符合式(3)的统计分布规律。由此可得三向等围压下的岩块轴向应变为
为微元体在单轴应力作用下的破坏应变,它符合式(3)的统计分布规律。由此可得三向等围压下的岩块轴向应变为
 (8)
(8)
对于一般三维问题,将 用
用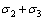 替换即可。由于该式两端均含有应变,因此需要迭代求解。
替换即可。由于该式两端均含有应变,因此需要迭代求解。
1.2 考虑损伤的倾斜节理面变形本构方程
图2所示岩体含一倾角为α的贯通节理AB,在三维应力作用下,节理面上的压应力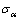 和剪应力
和剪应力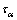 分别为:
分别为:
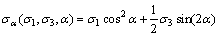 (9)
(9)
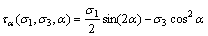 (10)
(10)
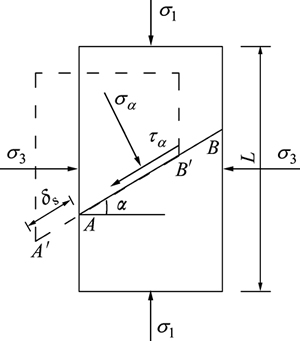
图2 含1条倾斜节理面的岩体
Fig. 2 Rock mass with one incline joint
在压应力作用下,节理面不但产生一定的闭合变形,而且上部岩块将沿节理面产生剪切滑移。因此,试件在压应力下的轴向变形由节理面的闭合变形及剪切滑移所组成。下面分别讨论这2种变形对试件轴向位移的贡献。
首先,在三向应力作用下,节理面产生的轴向闭合应变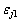 为[17]
为[17]
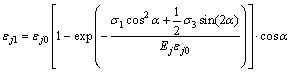 (11)
(11)
其中:Ej为节理面弹性模量(也称节理面闭合模量)。
其次,在三向应力作用下,试件还将发生沿节理面的剪切滑移,进而对试件轴向总应变产生影响。根据节理在剪切荷载作用下的本构关系[20],有
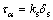 (12)
(12)
其中:ks为节理面切向刚度,MPa/m;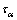 为节理面上的剪应力,MPa;
为节理面上的剪应力,MPa;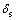 为沿节理面的剪切位移,m。可得试件由于沿节理面的剪切滑移而产生的轴向应变
为沿节理面的剪切位移,m。可得试件由于沿节理面的剪切滑移而产生的轴向应变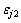 为
为
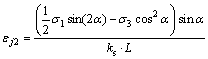 (13)
(13)
由此可得节理面在三向应力作用下产生的轴向总应变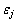 为
为
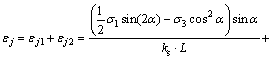
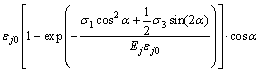 (14)
(14)
上面讨论的是单节理岩体,当试件含多条平行节理时,节理面产生的轴向总应变符合叠加原理,即由于节理变形产生的轴向总应变为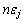 (其中,n为平行节理条数)。
(其中,n为平行节理条数)。
由推导过程可知上述计算是将节理面的弹性模量及剪切刚度作为定值来考虑,显然这是不合适的。一方面,节理面的弹性模量等力学参数与节理面两侧的岩块力学性质密切相关,当在压缩荷载作用下岩块的力学性质发生劣化后,必然会导致节理面的力学参数发生变化,进而影响节理面的闭合及剪切变形。另一方面,由式(14)可以看出:节理面的闭合及剪切变形与应力是一一对应关系,而实际的应力应变曲线则不然,因为峰值应力的存在,实际的应力一般都对应2个应变,即分别为峰前应变和峰后应变。因此,必须考虑节理力学性质的劣化,否则将无法得到正确的计算结果。为了简便,本文以完整岩块的损伤演化规律作为节理力学性质的劣化规律,即分别用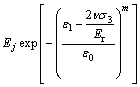 和
和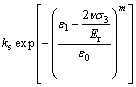 替换式(14)中的Ej和ks。
替换式(14)中的Ej和ks。
1.3 岩体压缩变形本构方程
综上所述,含n条倾角为α的平行节理岩体轴向应变为岩块轴向应变与节理轴向应变之和,即岩体轴向变形本构方程为
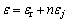 (15)
(15)
由式(15)可以看出:在轴向应变计算中不但需要岩块的弹性模量、泊松比等参数,而且需要节理面的弹性模量、切向刚度等参数,即岩体的总变形不但与岩块的参数有关,而且与节理面的参数有关,这与目前的研究结论是一致的。式(15)的求解方法是:首先由式(8)通过迭代求出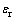 ,然而将相应的应力代入式(14)求出
,然而将相应的应力代入式(14)求出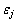 ,二者之和即为该应力所对应的轴向总应变。
,二者之和即为该应力所对应的轴向总应变。
2 算例分析
为了说明上述本构模型的合理性,以文献[21]中的试验资料为例进行说明,该模型如图3(a)所示,岩石弹性模量Er=6 949 MPa,泊松比υ=0.22。若假定岩石微元强度服从Weibull分布,将实测应力、应变(见图4)代入式(3),则通过拟合可得其分布参数为:m=3.335 2,ε0=0.012 8。由此可得岩石实测应力应变曲线及微元强度服从Weibull分布的理论应力应变曲线如图4所示。从图4可以看出:实测应力应变曲线与理论应力应变曲线较吻合。
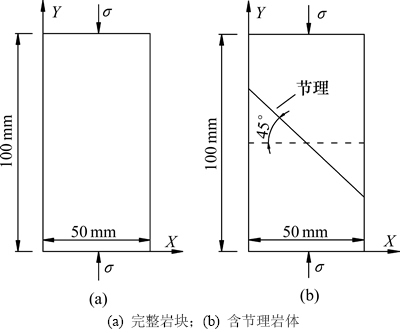
图3 计算模型示意图
Fig. 3 Calculation models
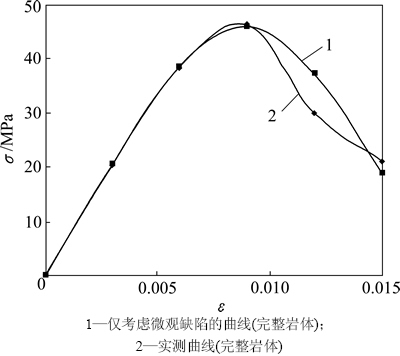
图4 计算应力-应变曲线
Fig. 4 Calculation stress-strain curves
下面对试件在三向受力状态下的力学特性进行讨论,计算模型如图3(b)所示,该模型含有1条45°节理。由于没有对实际节理参数进行测试,这里参照文献[17]取Ej=1 978 MPa,εj0=0.023,ks=2×104 MPa/m,L=0.1 m。通过施加不同围压,研究围压对试件应力应变曲线的影响,计算结果如图5所示。
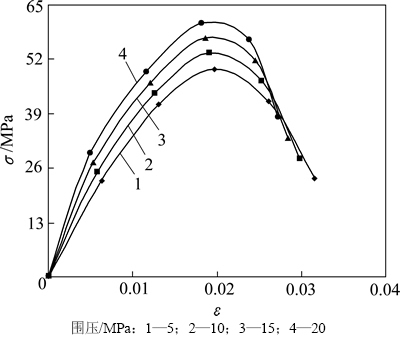
图5 不同围压下的应力-应变曲线
Fig. 5 Stress-strain curves under different confining pressures
由图5可以看出:
1) 随着围压增加,试件峰值强度逐渐变大,反映了围压对试件强度的影响,这与目前已有的研究结果一致[17]。
2) 随着围压增加,试件破坏时的最终应变减小,这与目前完整岩石在围压下的破坏规律不一致[18]。经分析认为由于本文研究对象为节理岩体,在岩体中试件轴向总应变不但包括岩块的轴向应变,更重要的是还包括由于节理的压缩变形及剪切滑移所产生的轴向应变,其中剪切滑移变形所占的比例更大,因此,随着围压增加,试件在同样的轴向荷载作用下所产生的剪切滑移逐渐减小,导致整个试件的轴向破坏总应变减小,这与完整岩石试件明显不同。
3) 虽然本文所提出的节理岩体损伤本构模型能够较好地反映节理岩体在三轴压缩荷载作用下的力学行为,但是与文献[18]中的模型相比,该模型对试件的弹性变形拟合结果还存在一定误差。一般地,对于不同围压下试件弹性阶段变形基本上是重合的,而该模型不能很好地反映这一点。经分析认为:曹文贵等[18]所提出的模型是对不同围压下的曲线分别进行拟合得到的,即不同围压下本构模型中的待定常数不一样,这固然可以使试验曲线与理论曲线较吻合,但在没有三轴试验结果的情况下无法得到试件具体的本构关系表示式。而本文所提出的模型虽然存在一定误差,但其采用的拟合参数是试件单轴压缩曲线的拟合参数,即仅有单轴压缩曲线便能较好地对试件在不同围压下的力学特性进行估计,很好地实现其预测功能,以克服目前大多数模型仅能提供验证功能的不足。
4) 为了简便,本文对节理在压缩荷载作用下的力学性能简单地用岩块的损伤来体现,这是不恰当的,需对此进行改进。
5) 本模型没有考虑试件可能沿节理面发生的剪切破坏,即认为节理面强度足够大,这显然与大多数实际岩体不符。实际岩体中的节理面通常为软弱面,岩体的破坏通常沿节理面发生,因此,本文所提出的本构模型仅适用于节理面强度足够大的岩体。
3 结论
1) 基于岩体结构力学观点,分别采用基于统计损伤模型的弹性损伤变形元件和考虑结构面闭合及滑动的变形元件分别描述岩块和结构面在压缩荷载作用下的变形规律,进而建立了相应的节理岩体压缩损伤本构模型。
2) 针对最大拉应变破坏准则不适合于描述三向受力状态下岩石破坏这客观情况,根据复杂受力条件下的Mises屈服准则推导出三向状态下的最大主应变与围压之间的关系,进而建立考虑三向受力条件下的节理岩体损伤本构模型。
3) 围压不但对试件峰值强度有一定影响,而且对试件的变形尤其是沿节理面的滑移变形有较大影响。
参考文献:
[1] 谢和平. 岩石、混凝土损伤力学[M]. 徐州: 中国矿业大学出版社, 1990: 1-5.
XIE Heping. Rock concrete damage mechanics[M]. Xuzhou: Press of China University of Mining Science & Technology, 1990: 1-5.
[2] Moradian Z A, Ballivy G, Rivard P, et al. Evaluating damage during shear tests of rock joints using acoustic emissions[J]. Int J Rock Mech Min Sci, 2010, 47: 590-598.
[3] 朱红光, 谢和平, 易成, 等. 岩石材料微裂隙演化的CT识别[J]. 岩石力学与工程学报, 2011, 30(6): 1230-1238.
ZHU Hongguang, XIE Heping, YI Cheng, et al. CT identification of microcracks evolution for rock materials[J]. Chinese Journal of Rock mechanics and Engineering, 2011, 30(6): 1230-1238.
[4] Tang C A. Numerical studies of the influence of microstructure on rock failure in uniaxial compression. PartⅠ: Effect of heterogeneity[J]. Int J Rock Mech Min Sci, 2000, 37(4): 555-569.
[5] Zhou J W, Xu W Y, Yang X G. A microcrack damage model for brittle rocks under uniaxial compression[J]. Mechanics Research Communications, 2010, 37(4): 399-405.
[6] Xie N, Zhu Q Z, Xu L H, et al. A micromechanics-based elastoplastic damage model for quasi-brittle rocks[J]. Computers and Geotechnics, 2011, 38(8): 970-977.
[7] Hamdi E, Romdhane N B, Le Cleach J M. A tensile damage model for rocks: Application to blast induced damage assessment[J]. Computers and Geotechnics, 2011, 38(2): 133-141.
[8] 尹立明, 张培森. 双结构面对岩体强度影响的模拟分析[J]. 采矿与安全工程学报, 2010, 27(4): 600-603.
YIN Liming, ZHANG Peisen. Simulation analysis of rock mass strength affected by dual structural plane[J]. Journal of Mining & Safety Engineering, 2010, 27(4): 600-603.
[9] 狄圣杰, 单治钢, 宋庆滔. 节理玄武岩强度特性三维离散元压缩模拟试验[J]. 中南大学学报(自然科学版), 2013, 44(7): 2903-2909.
DI Shengjie, SHAN Zhigang, SONG Qingtao. Numerical compression test on strength property of jointed basalts by 3D discrete element method[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2903-2909.
[10] Wang T T, Huang T H. A constitutive model for the deformation of a rock mass containing sets of ubiquitous joints[J]. Int J Rock Mech Min Sci, 2009, (46): 521-530.
[11] Swoboda G, Shen X P, Rosas L. Damage model for jointed rock mass and its application to tunneling[J]. Computers and Geotechnics, 1998, 22(3/4): 183-203.
[12] 杨云浩, 徐卫亚. 基于节理岩体损伤本构的硐室位移反分析研究与应用[J]. 中南大学学报(自然科学版), 2012, 43(7): 2723-2732.
YANG Yunhao, XU Weiya. Displacement-based back-analysis using damage mechanics constitutive model for jointed rock mass and its application in underground opening[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2723-2732.
[13] 朱珍德, 渠文平, 蒋志坚. 岩石细观结构量化试验研究[J]. 岩石力学与工程学报, 2007, 26(7): 1313-1324.
ZHU Zhende, QU Wenping, JIANG Zhijian. Quantitative test study on mesostructure of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1313-1324.
[14] 蒲成志, 曹平, 衣永亮. 单轴压缩下预制2 条贯通裂隙类岩材料断裂行为[J]. 中南大学学报(自然科学版), 2012., 43(7): 2708-2716.
PU Chengzhi, CAO Ping, YI Yongliang. Fracture for rock-like materials with two transfixion fissures under uniaxial compression[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2708-2716.
[15] 刘红岩, 黄妤诗, 李楷兵, 等. 预制节理岩体试件强度及破坏模式的试验研究[J]. 岩土力学, 2013, 34(5): 1235-1241, 1246.
LIU Hongyan, HUANG Yushi, LI Kaibing, et al. Test study of strength and failure mode of pre-existing jointed rock mass[J]. Rock and Soli Mechanics, 2013, 34(5): 1235-1241, 1246.
[16] Tang C A. Numerical simulation of progressive rock failure and associated seismicity[J]. Int J Rock Mech Min Sci, 1997, 34(2): 249-261.
[17] 孙广忠, 孙毅. 岩体力学原理[M]. 北京: 科学出版社, 2011: 51-59.
SUN Guangzong, SUN Yi. Principle of rock mass mechanics[M]. Beijing: Science Press, 2011: 51-59.
[18] 曹文贵, 赵衡, 张玲, 等. 恒应变率下的岩石三轴动态变形过程模拟方法[J]. 岩土工程学报, 2010, 32(11): 1658-1664.
CAO Wengui, ZHAO Heng, ZHANG Ling, et al. Simulation method of dynamic triaxial deformation process for rock under invariable strain rate[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1658-1664.
[19] Krajcinovic D, Silva M A G. Statistical aspects of the continuous damage theory[J]. Int J Solids Structures, 1982, 18(7): 55-562.
[20] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002: 84-93.
XIA Caichu, SUN Zongqi. Engineering rock mass joint mechanics[M]. Shanghai: Tongji University Press, 2002: 84-93.
[21] 凌建明, 孙钧. 脆性岩石的细观裂纹损伤及其时效特征[J]. 岩石力学与工程学报, 1993, 12(4): 304-312.
LING Jianming, SUN Jun. On mesocrack damage of brittle rocks and its time-dependent characteristics[J]. Chinese Journal of Rock mechanics and Engineering, 1993, 12(4): 304-312.
(编辑 陈灿华)
收稿日期:2014-03-10;修回日期:2014-05-21
基金项目(Foundation item):国家自然科学基金资助项目(41002113,41162009);教育部科学技术研究重点项目(211175);中央高校基本科研业务费专项资金资助项目(2014ZY45);2011年度北京市属高等学校人才强教深化计划人才创新团队项目(PHR201107143) (Projects(41002113, 41162009) supported by the National Natural Science Foundation of China; Project(211175) supported by the Key Project of Chinese Ministry of Education; Project(2014ZY45) supported by the Fundamental Research Funds for the Central Universities; Project(PHR201107143) supported by the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality)
通信作者:刘红岩,博士,教授,从事岩石力学方面的教学与研究工作;E-mail: lhyan1204@126.com