DOI： 10.11817/j.issn.1672-7207.2020.03.008

避障模式下深海采矿系统动力学分析

徐海良^{1, 2},彭能¹,杨放琼^{1, 2}

（1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083）

摘要:为研究避障模式下深海采矿系统中中间仓的运动规律，基于虚拟样机技术建立5 km硬管水力输送系统虚拟样机模型，根据现有的全区域覆盖算法，提出3种可能的避障模式(圆形、矩形、折返避障模式)，分析不同避障模式、避障速度、障碍物距离对中间仓运动特性的影响，并进行模拟实验研究。研究结果表明：中间仓的运动主要发生在集矿机前进的方向上；在起始点附近，折返避障模式下，避障结束时中间仓位移的最大值达3.0 m，比圆形和矩形避障模式的高；当避障速度从0.4 m/s增加到1.0 m/s时，中间仓位移平均值的增加幅度小于0.2 m；障碍物距离对中间仓运动特性影响较大，中间仓位移平均值和最大值随障碍物距离的增加而逐渐减少；在进行采集路径规划时，尽量使障碍物距离大于200 m。因此，对集矿机进行避障算法设计时，不仅要考虑算法的可行性，还要考虑整个系统在不同避障模式下动力学特性。

关键词:深海采矿；虚拟样机；动力学分析；避障模式；中间仓

中图分类号:TH113.2+2     文献标志码:A          开放科学(资源服务)标识码(OSID)

文章编号:1672-7207（2020）03-0641-09

Dynamic analysis of deep sea mining system in obstacle avoidance mode

XU　Hailiang^{1, 2}, PENG　Neng¹, YANG　Fangqiong^{1, 2}

(1. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China；

2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

Abstract: To study the motion characteristics of the buffer in the deep sea mining system in the obstacle avoidance mode, a virtual prototype model of 5 km hard-tube hydraulic conveying system was established based on the virtual prototyping technology. Three possible obstacle avoidance modes(circle, rectangle, reciprocating mode) were proposed according to the existing full-area coverage algorithm. The effects of the type of obstacle, obstacle avoidance speed and obstacles distance on the kinetic characteristic of buffer were analyzed. And the simulation experiment was carried out. The results show that the movement of the buffer mainly occurs in the forward direction of mining machine. The maximum displacement of buffer is up to 3.0 m near the initial point, which is higher than those of circular and rectangular obstacle avoidance modes. When the obstacle avoidance speed increases from 0.4 m/s to 1.0 m/s, the average increment of displacement of buffer is less than 0.2 m. The obstacle distance has a great influence on the motion characteristics of the buffer. The average and maximum values of displacement of buffer decrease with the increases of obstacle distance. When planning the acquisition path, it is recommended to make the distance between obstacle and buffer greater than 200 m. Therefore, when designing the obstacle avoidance algorithm for the mining machine, it is suggested to consider not only the feasibility of the algorithm, but also the dynamics characteristics of the whole system in different obstacle avoidance modes.

Key words: deep sea mining; virtual prototype; dynamics analysis; obstacle avoidance mode; buffer

2016年，我国在南海某海域进行的深海采矿泵管输送系统海上实验成功通过专家组验收，实现了我国从湖试向海试的历史性转变^[1]。对深海采矿系统而言，目前研究多针对硬管水力输送系统，该系统由海面支撑船、扬矿硬管、中间仓、扬矿软管、集矿机等子系统组成^[2]。作为深海采矿系统装备的重要组成，硬管水力提升系统的动力学关系到采矿系统总体设计、安全校核以及系统运行控制等诸多方面，且采矿系统需在深达数千米的海底完成采集作业，海底环境复杂未知，采集过程中障碍物难以避免，避障过程中系统动力学问题不容忽视。在采矿系统动力学方面，国内外学者进行了一些研究。简曲等^[3-4]通过空间“梁”单元离散元模型，采用数学建模与模拟实验相结合的方法，分析了输送软管的动态特性；徐海良等^[5-6]采用有限元分析软件分析软管形态、集矿机位置对软管内流场分布、压力损失的影响，并得到了管线系统在海流中运动的阻力计算公式；LI等^[7-8]基于ADAMS/VIEW建立1 km硬管水力输送采矿系统虚拟样机，研究了不同联动速度和海流速度以及顺流逆流等情况下采矿系统的空间构型；戴瑜等^[9-12]借助ADAMS/VIEW和RecurDyn/Track建立1 km采矿系统虚拟样机模型，分析系统在横向折返式与纵向折返式2种不同采集路径下的系统联动特性，证明了这2种采集模式的可行性；并得出了系统在直线行驶、曲线转弯、爬坡越沟等行走模式下的运动学规律；王刚等^[13]分别采用多体动力学和有限元分析软件，分析了系统布放以及三维联动过程的运动学和动力学特性；PARK等^[14]从理论上对比计算了不同采集路径，并提出了针对非规则区域的全区域覆盖算法；OH等^[15]采用商业软件DAFUL建模，并分析采矿系统的运动特性，得到中间仓软管连接段所受的流体载荷及变形估计值。在集矿机避障算法上，史春雪等^[16]基于蚁群算法，提出邻近搜素和中线偏移避障策略，并验证了该算法的可行性；杨晓等^[17]基于LabVIEW与MATLAB混合编程，利用声学与光学器件的信息融合技术，给出了集矿机导航避障控制的详细流程。目前，对采矿系统动力学方面的研究主要集中在静态模式下的管线系统的液动力，管线系统节点受力、管线空间构型、正常采集模式下的系统联动特性以及理论上避障算法的可行性方面，而对在避障过程中采矿系统动力学的研究较少。为此，本文作者以避障模式为基础，研究不同避障模式、障碍物位置、避障速度对中间仓运动特性的影响，为实际深海采矿路径规划与避障算法设计提供理论指导。

1 硬管水力提升系统虚拟样机模型

1.1　模型分析与简化

深海采矿管线系统在采集作业过程中表现为大变形、强时变、非线性等动力学特性^[18]。考虑到采矿系统的复杂性和虚拟样机建模思想，对采矿系统进行简化：

1) 只考虑采矿船、中间仓、集矿机的质量、尺寸、质心位置以及与管道的连接方式，不考虑其内部细节特征。

2) 扬矿管道附带有电缆等通讯、电控设备。建模时，不考虑附属部件而将其质量折算成部分管道质量。

3) 实际中，管道之间有专门的连接机构，本文不考虑具体的连接机构，而将其简化为无质量、无长度的轴套力连接。

基于上述假设及ADAMS/VIEW宏命令，得到5 km硬管水力输送系统如图1所示。

图1　采矿系统虚拟样机

Fig. 1　Virtual prototype of mining system

1.2　参数设置

图1所示虚拟样机模型中，采矿船位于(0, 0, 0)处，中间仓质心坐标(0,-4 600, 0)，软管长度为400 m，软管上端连接中间仓，下端与集矿机相连。为了保证集矿机较大的采集范围，并且减少软管对集矿机的牵制作用，软管部分安装浮体球^[19]，同时设定海流方向与系统运动方向相反，海面流速0.772 m/s，海底流速0.15 m/s。

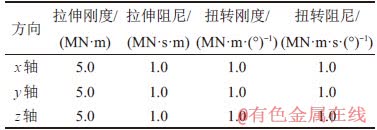
根据假设，并参考文献[20]中的参数设计方法，各部分参数定义如下：硬管材料为P110钢，总长为4.6 km，离散为460段，每段长10 m；管道外径为219 mm，管道壁厚为12.7 mm；软管总长400 m，离散为100段，每段长4 m，内外径与硬管的一致。轴套力是虚拟样机建模中常用的柔性连接形式。轴套力参数可参考文献[21]中的计算方法：k₁=EA/L；k₂=k₃=GA/L；k₄=Gπd⁴/L；k₅=EI/L；k₆=GI/L，其中：k₁为y方向拉伸刚度系数；k₂和k₃分别为x和z方向剪切刚度系数；k₄为y方向扭转刚度系数；k₅和k₆分别为x和z方向弯曲刚度系数；G，E，L，A，d分别管道的弹性模量、剪切模量、刚体单元长度、截面积、当量直径。硬管轴套力参数与软管轴套力参数不同，但计算方法一致。硬管轴套力参数计算结果如表1所示。

表1　轴套力参数

Table 1　Brushing force parameter

1.3　扬矿管液动力

采矿系统在深海中运动时，由于流体的黏性，管道会受到流体阻力的影响。采矿系统中的扬矿管道属于细长杆，细长杆在流体中的作用力可以用Morison方程等效^[22-23]。为匹配硬管建模时的坐标系统，规定x方向为海流方向，x-z为海平面，y正向为由海面指向海底。采矿船与扬矿管的连接处为坐标原点。考虑到硬管系统相对海水有运动速度，根据相对运动，Morison方程为

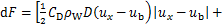
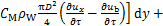
(1)

式中：C_D为阻力系数^[24]，为1.8，C_M为惯性力系数，为0.46；为海水密度，kg/m³；u_x为水质点的平均速度，m/s，D为扬矿管外径，m；u_b为管线单元质心的运动速度，m/s。

2 集矿机避障行走模式分析

采矿系统联动时，中间仓在采矿船的拖动下随系统一起运动，其运动规律主要由采矿船的运动形式决定。但当采矿船不动，只有集矿机运动时，中间仓的运动具有随机性，且中间仓内部设有复杂的给料机构，中间仓晃动过大时，易造成内部流场的紊乱而导致射流口堵塞。根据前人的研究，容腔内液体的晃动会造成系统非线性振动，同时也会造成管道连接处的疲劳破坏^[25]。因此，实际采矿时，尽量保证中间仓处于稳定状态。具体做法为：根据集矿机采集范围，将矿区划分为若干小区域，在一个小区域内，采矿船不动，集矿机完成采集作业，一个区域采集完成后，通过系统联动“搬移”到另一个区域继续采集。本文将采矿船不动，集矿机单独采集的区域作为一个单独采集区，简称单采区。

深海环境复杂，地形地貌未知，单采区内集矿机难以保持理想的直线行驶。当遇到海底不明障碍物、地形坑洼等复杂情况时，集矿机需采取特殊的避障采集模式。实际中障碍物相对于采矿系统的位置分布具有随机性，但是本文重点分析集矿机在绕过障碍物过程中中间仓的运动特性。因此只考虑集矿机前进方向上的障碍物。采矿系统三维示意图如图2所示。

另外，深海障碍物形状、大小无规律性。实际开展采集作业时，由于集矿机行走受限，难以使集矿机严格按照障碍物边缘行走，因此，可采用图像处理中的特征识别和边缘检测方法，根据障碍物形状、大小将障碍物分类，然后根据实时检测的障碍物，为集矿机匹配合适的行走避障模式。

为便于仿真分析，将处理后障碍物形状假设为规则的矩形和圆形，且不考虑集矿机越过低矮障碍物的越障形式。根据集矿机的行走模式和现有的全区域覆盖算法，作如下假设：若障碍物横向尺寸大于2倍集矿机的采集宽度，则采用折返避障模式；否则，再进一步根据障碍物的形状，规划出圆形和矩形避障行走模式。

图2　采矿系统三维示意图

Fig. 2　3D schematic diagram of mining system

3种避障模式(圆形、矩形、折返避障模式)的避障过程如图3所示。在圆形避障模式下，集矿机在障碍物前方以圆弧前进的方式绕过障碍物，此时，集矿机横向和纵向均有速度分量，转向较为平缓；在矩形避障模式下，集矿机在障碍物前方停止初始的前进运动，然后转向90°，向另一个方向行驶一定距离，然后按照初始前进的方向绕过障碍物；在折返避障模式下，由于障碍物横向尺寸较大，以降低漏采区为目标，集矿机在障碍物前方以多次折返的方式绕过障碍物，完成矿石资源的采集。

图3　避障模式示意图

Fig. 3　Schematic diagram of obstacle avoidance mode

为控制无关变量，仿真中设置圆形障碍物半径为25 m，矩形障碍物长度为25 m，宽度为50 m，集矿机初始位置距离中间仓为350 m，并规定集矿机从初始点出发向中间仓运动。

3 仿真分析

3.1　避障模式对比分析

中间仓是矿石颗粒从集矿机到海面采矿船的中间枢纽站，上连接硬管，下连接软管。一个单采区内，集矿机拖动软管，可能使软管摆动而给中间仓造成一定的扰动作用。如图2所示，中间仓y方向的运动受到硬管限制，因此本文重点研究中间仓x和z方向的运动。仿真过程中，针对3种避障模式，通过编写运动驱动函数，设置合速度均为0.5 m/s，得到3种不同避障模式下中间仓x和z方向的位移随时间的变化曲线，如图4所示。

由图4(a)可知：在不同避障模式下，中间仓的x方向位移差别很大。0~100 s内，3种避障模式下，中间仓位移曲线几乎重合；100 s附近，位移稳定在1.5 m左右。这是由于前100 s，3种模式下集矿机均做匀速直线运动，100 s时，集矿机开始转向，x方向的运动速度下降。100 s后，3种避障模式下，中间仓x方向位移继续增加。其中，折返避障模式下，中间仓x方向的位移随时间变化速度增长最快，几乎与前100 s的相当；圆形避障模式次之；但矩形避障模式下，100~150 s内，x方向位移几乎保持不变；150 s后，与折返避障模式有同样的速度增加。这是因为在100~150 s内，矩形避障模式x方向速度为0 m/s，z方向的速度为0.5 m/s；而根据圆弧的驱动方程，100~150 s内，x和z方向速度均不为0 m/s；而折返避障模式下，集矿机以相同的速度反方向运动，但由于软管处于松弛状态，在惯性作用下，中间仓x方向的位移继续增加。250 s左右，避障结束，折返避障模式下中间仓位移达到最大值3.0 m，圆形和矩形避障模式最大值为2.8 m，略低于折返避障模式最大值。这是因为在折返式模式下，集矿机行走路径折返次数多，造成软管的摆动作用较大，从而中间仓的运动受到的影响也越大。因此，实际执行避障过程时，建议采用圆形和矩形避障模式。

图4　3种避障模式下中间仓位移随时间的变化曲线

Fig. 4　Curves of displacement of buffer with time in three obstacle avoidance modes

由图4(b)可知：在前100 s内，3种模式下，中间仓z方向位移在零线附近变化；100 s后，z方向的位移变化均在-0.05~0.12 m之间。与图4(a)对比可知，z方向的位移远小于x方向的位移。这是因为3种避障模式下，集矿机的运动主要发生在x方向。

3.2　避障速度对中间仓位移的影响

由于集矿机作业环境的特殊性，参考文献[12,26]，集矿机运行速度范围控制在0.4~1.0 m/s，因此取集矿机驱动速度为0.4，0.6，0.8和1.0 m/s，障碍物距离中间仓350 m。对比分析集矿机的避障速度对中间仓运动的影响，并将不同速度下的仿真数据求平均值和最大值，得到如图5所示的中间仓x方向位移(简称“中间仓位移”)随速度的变化曲线。

从图5(a)可以看出：在圆形和矩形避障模式下，中间仓位移的平均值随避障速度增加而增加，但增加幅度在0.1~0.2 m之间；说明速度在0.4~1.0 m/s之间对中间仓位移平均值影响不大。而在折返避障模式下，中间仓位移几乎不受避障速度的影响。但从总体上看，当避障速度0.4 m/s增加到1.0 m/s时，在圆形避障模式下，中间仓位移均比矩形和折返避障模式的小。这是因为，按圆弧方向行走，集矿机x和z方向的速度变化较小，由速度切换而产生的加速度较小，软管和中间仓受到的影响也越小；而折返避障模式和矩形避障模式下，集矿机运行速度在x和z方向进行多次变换，从而增加了系统的不稳定性。

由图5(b)可知：中间仓位移的最大值随避障速度增加而增加。在圆形和矩形避障模式下，当避障速度从0.4 m/s增加到1.0 m/s时，中间仓位移的最大值增加幅度在1 m左右；在折返避障模式下，当避障速度从0.4 m/s增加到1.0 m/s，位移的最大值从3.1 m增加到5.2 m；且避障速度大于0.6 m/s，中间仓位移的最大值迅速增加。因此，相对于其他2种避障模式，避障过程中当折返避障模式无法避免时，应控制避障速度低于0.6 m/s。

3.3　障碍物距离对中间仓运动的影响

障碍物分布于海底的位置具有随机性，针对障碍物与中间仓的距离(障碍物距离)对中间仓运动的影响规律进行研究，以针对不同位置提供不同的避障方案。集矿机的运动范围受到软管牵制，在初始位置时，集矿机距离中间仓350 m；集矿机在远离初始点向中间仓方向进行避障时，障碍物距离越小，受到软管的牵制作用越大，中间仓的运动受到的影响越大。在障碍物距离分别为100，150，200，250和300 m，避障速度均为0.5 m/s时，3种避障模式下障碍物距离对中间仓位移的影响规律如图6所示。

图 5　不同避障模式下避障速度对中间仓位移的影响

Fig. 5　Influence of speed on displacement of buffer at different obstacle avoidance modes

图 6　不同避障模式下避障距离对中间仓位移的影响

Fig. 6　Influence of distance on displacement of buffer at different obstacle avoidance modes

从图6可看出，障碍物距离不同时，中间仓位移的平均值和最大值相差较大。随着障碍物距离增加，3种模式下中间仓位移的平均值和最大值均呈下降趋势。当障碍物距离为100 m时，折返式模式下，位移平均值接近3.5 m，圆形和矩形避障模式下为3.2 m左右；障碍物距离增加到300 m时，折返避障模式下，位移平均值降为1.9 m左右，圆形和矩形避障模式下平均值降为1.7 m左右。而障碍物距离从100 m增加到200 m时，障碍物距离每增加50 m，位移平均值下降幅度为0.2 m左右；障碍物距离从200 m增加到300 m时，障碍物距离每增加50 m，位移平均值幅度在0.5 m左右，下降速度明显高于障碍物距离为100~200 m时的下降速度。障碍物距离从300 m增加到350 m时，位移平均值几乎不变，稳定在2.0 m左右。这是因为障碍物距离小于200 m时，软管已严重变形，对集矿机的运动屏蔽能力减弱。当障碍物距离为100~200 m时，中间仓位移平均值与最大值下降趋势缓慢；当障碍物距离大于200 m时，软管逐渐舒展，对集矿机的运动屏蔽作用加强；当障碍物距离为200~300 m时，中间仓位移平均值和最大值下降较大；当障碍物距离为300~350 m时，软管已处于完全舒展状态，对集矿机的屏蔽效应也达到最大，因此，障碍物距离为300~350 m范围内，中间仓位移平均值和最大值几乎不变。

由图6(b)可知：折返避障模式下，障碍物距离100 m时，中间仓位移最大值接近5.0 m；圆形和矩形避障模式下，中间仓位移最大值为4.75 m，比折返避障模式的略低。当障碍物距离为300~350 m时，折返避障模式下，位移最大值稳定在3.2 m，圆形和矩形避障模式下，位移最大值稳定在3.0 m左右，且位移最大值随障碍物距离的变化趋势与平均值随障碍物距离的变化趋势几乎一致。因此，进行避障路径规划时，要考虑障碍物与中间仓的距离，尽量避免障碍物距离小于200 m。

4 实验验证

利用中南大学机电工程学院高性能复杂制造国家重点实验室的实验设备，根据相似原理，搭建模拟实验平台，对不同避障模式下中间仓的运动规律进行实验研究，以验证仿真结果的正确性。模拟实验平台如图7所示。实验系统包含控制系统、实验台和测量系统。实验中所用管道采用直径为1 mm的铜丝代替；中间仓采用边长为30 mm的立方体铝块代替；软管采用内径为2 mm、外径为3.2 mm的PVC管道代替；自动循迹小车代替集矿机；使用工业风扇产生的风力模拟海洋液动力环境。实验前，首先根据仿真设置，在集矿机前进方向上布置障碍物，然后用黑色胶带表示3种避障行走模式在平台上铺设白色底面，并粘贴黑色胶带模拟集矿机3种行走轨迹。调整激光探测头的高度使其与铝块中心平齐。同时，根据小车行走轨迹，用C语言编写自动寻迹程序，将其烧写到51单片机开发板中。实验过程中，使用激光探测头实时测量中间仓的位移情况，并通过数据采集卡将位移数据采集到计算机中。

图 7　模拟实验平台

Fig. 7　Experimental platform

实验结果与仿真结果对比如表2所示。从表2可见：中间仓位移实验结果比仿真结果大。这是因为仿真时设置了集矿机与海底接触面之间的渗透值，而实验平台无法设置，实验时存在打滑现象，导致实验结果偏高。但二者之间的相对误差在8%以内，表明仿真结果的可信度较高。

表2　中间仓位移实验平均值与仿真平均值对比

Table 2　Comparison of average displacement of buffer in simulation and experiment

5 结论

1) 初始点处，3种避障模式下，中间仓x方向的位移远大于z方向的位移；在折返式避障模式下，中间仓位移的最大值达3.0 m，大于圆形和矩形避障模式下的位移最大值，因此，初始点附近建议采取圆形避障模式和矩形避障模式。

2) 在3种避障模式下，避障速度中间仓位移平均值影响较小，避障速度从0.4 m/s增加到1.0 m/s时，位移平均值增幅仅为0.2 m。但速度大于0.6 m/s时，折返避障模式下，中间仓位移的最大值增幅比圆形和矩形避障模式的高；因此，从位移最大值的角度，采用折返式避障模式时，尽量控制避障速度不超过0.6 m/s。

3) 中间仓位移随障碍物距离的增加而减少，且障碍物距离在200~300 m的范围内，位移平均值和最大值的下降速率最大；300~350 m范围内，位移平均值与最大值几乎不变。因此，避障算法设计时，应考虑中间仓与障碍物之间的距离，尽量使障碍物距离大于200 m。

4) 中间仓位移实验平均值与仿真值的相对误差在8%以内，表明仿真结果的可信度较高。

参考文献：

[1] XU Hailiang, CU Cong, WU Bo. Theoretical analysis of effect of solid phase on cavitation performance of deep-sea mining pump[J]. Journal of Chongqing University, 2018, 17(2):49-54.

[2] VOLKMANN S E, KUHN T, LEHNEN F. A comprehensive approach for a techno-economic assessment of nodule mining in the deep sea[J]. Mineral Economics, 2018, 31(3): 319-336.

[3] 简曲, 何永森, 王明和, 等. 大洋采矿输送软管动力特性的数值研究[J]. 海洋工程, 2001, 19(1): 59-64.

JIAN Qu, HE Yongsen, WANG Minghe, et al. Numerical study of dynamic behavior of flexible pipes in deep sea mining[J]. The Ocean Engineering, 2001, 19(1): 59-64.

[4] 崔凯, 李宝元, 纪峥. 深海采矿系统中输运软管的数值模拟[C]//全国工业与环境流体力学会议. 大连, 2001: 199-205.

CUI Kai, LI Baoyuan, JI Zheng. Numerical simulation of conveying hose in deep sea mining system[C]//National Conference on Industry and Environment Fluids Mechanics, Dalian, China, 2001: 199-205.

[5] 徐海良, 李立, 吴波, 等. 软管和矿车对深海采矿系统的影响规律分析[J]. 计算机仿真, 2017, 34(1): 231-235, 287.

XU Hailiang, LI Li, WU Bo, et al. Influence of flexible hose and nodule collector analysis on deep-sea mining transporting system[J]. Computer Simulation, 2017, 34(1): 231-235, 287.

[6] 徐海良, 何清华. 深海采矿输送系统的运动和载荷分析[J]. 湖南科技大学学报(自然科学版), 2005, 20(1): 21-24.

XU Hailiang, HE Qinghua. Nonlinear mechanical analysis theory of the sea mining flexible mineral transporting pipe[J]. Journal of Hunan University of Science & Technology(Natural Science Edition), 2005, 20(1): 21-24.

[7] LI Yan, LIU Shao Jun, LI Li. Dynamic analysis of deep-ocean mining pipe system by discrete element method[J]. China Ocean Engineering, 2007, 21(1):175-185.

[8] 李艳, 刘少军, 禹宏云. 基于多刚体离散元模型的深海采矿系统动力学分析[J]. 中南大学学报(自然科学版), 2006, 37(4): 742-747.

LI Yan, LIU Shaojun, YU Hongyun. Dynamic analysis of deep-ocean mining system based on multi-rigid-body discrete element model[J]. Journal of Central South University(Science and Technology), 2006, 37(4): 742-747.

[9] 戴瑜, 刘少军. 深海采矿整体系统动力学建模及联动开采作业过程快速仿真分析[J]. 机械工程学报, 2012, 48(9): 79-88.

DAI Yu, LIU Shaojun. Establishment of the dynamic model of the total deep ocean mining system and fast simulation of its integrated operation process[J]. Chinese Journal of Mechanical Engineering, 2012, 48(9): 79-88.

[10] DAI Yu, LIU Shaojun. An integrated dynamic model of ocean mining system and fast simulation of its longitudinal reciprocating motion[J]. China Ocean Engineering, 2013, 27(2): 231-244.

[11] 戴瑜, 张健, 张滔, 等. 基于多体动力学模型集成的深海采矿系统联动仿真[J]. 机械工程学报, 2017, 53(4): 155-160.

DAI Yu', ZHANG Jian, ZHANG Tao, et al. Motion simulation of the deep ocean mining system based on its integrated multi-body dynamic model[J]. Chinese Journal of Mechanical Engineering, 2017, 53(4): 155-160.

[12] 张滔, 戴瑜, 刘少军, 等. 深海履带式集矿机多体动力学建模与行走性能仿真分析[J]. 机械工程学报, 2015, 51(6): 173-180.

ZHANG Tao, DAI Yu, LIU Shaojun, et al. Multi-body dynamic modeling and mobility simulation analysis of deep ocean tracked miner[J]. Chinese Journal of Mechanical Engineering, 2015, 51(6): 173-180.

[13] 王刚, 徐昱. 深海采矿系统计算机模拟[J]. 实验室研究与探索, 2006, 25(1): 49-52.

WANG Gang, XU Yu. Computer simulation research on deep-sea mining system[J]. Laboratory Research and Exploration, 2006, 25(1): 49-52.

[14] PARK S J, YEU T K, YOON S M, et al. A study of sweeping coverage path planning method for deep-sea manganese nodule mining robot[C]//Oceans 2011. Waikoloa,USA: IEEE, 2011: 1-5.

[15] OH J W, LEE C H, HONG S, et al. A study of the kinematic characteristic of a coupling device between the buffer system and the flexible pipe of a deep-seabed mining system[J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6(3): 652-669.

[16] 史春雪, 卜英勇, 罗柏文, 等. 基于蚁群算法深海采矿机器人工作路径规划[J]. 海洋工程, 2008, 26(2): 119-123.

SHI Chunxue, BU Yingyong, LUO Bowen, et al. Path planning for deep sea mining robot based on ant colony algorithm[J]. The Ocean Engineering, 2008, 26(2): 119-123.

[17] 杨晓, 王敏. 基于LabVIEW深海集矿机避障导航控制系统设计[J]. 机械设计与制造, 2018(8): 159-161, 165.

YANG Xiao, WANG Min. Analysis of obstacles avoidance and navigation control system of deep-sea mining vehicle based on LabVIEW[J]. Machinery Design & Manufacture, 2018(8): 159-161, 165.

[18] 冯福璋, 冯雅丽, 张文明. 基于有限元和虚拟样机技术的螺纹与球铰连接扬矿管整体水平运动[J]. 北京科技大学学报, 2006, 28(12): 1152-1156.

FENG Fuzhang, FENG Yali, ZHANG Wenming. Lateral movement of lifting strings connected by screwed joints and spherical joints in deep sea by finite element analysis and virtual prototype technology[J]. Journal of University of Science and Technology Beijing, 2006, 28(12): 1152-1156.

[19] 吴波, 程小明, 田超, 等. 深海采矿系统水动力技术研究综述[J]. 中国造船, 2016, 57(3): 204-214.

WU Bo, CHENG Xiaoming, TIAN Chao, et al. Research advance on hydrodynamic techniques in deep sea mining system[J]. Shipbuilding of China, 2016, 57(3): 204-214.

[20] 李艳. 基于三维离散元管线模型的深海采矿1000 m海试系统整体联动动力学研究[D]. 长沙: 中南大学机电工程学院, 2009: 78-84.

LI Yan. Dynamic analysis of 1000 m ocean pilot mining system based on three-dimensional discrete element method pipe model[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2009: 78-84.

[21] 徐昱. 1000米海试深海采矿系统布放回收过程的虚拟样机研究[D]. 长沙: 中南大学机电工程学院, 2004: 45-54.

XU Yu. Virtual prototype research on the deployment process of 1000 m sea trail deep mining system[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2004: 45-54.

[22] 柏君励, 马宁, 顾解忡. 波流对不同淹没深度水平圆柱的载荷分析[J]. 上海交通大学学报, 2018, 52(8): 938-945.

BAI Junli, MA Ning, GU Xiechong. Wave-current loads on the horizontal cylinder with varying submergence depths[J]. Journal of Shanghai Jiao Tong University, 2018, 52(8): 938-945.

[23] RAED K, GUEDES SOARES C. Variability effect of the drag and inertia coefficients on the Morison wave force acting on a fixed vertical cylinder in irregular waves[J]. Ocean Engineering, 2018, 159: 66-75.

[24] LIU Chunguang, SUN Guoshuai. Calculation and experiment for dynamic response of bridge in deep water under seismic excitation[J]. China Ocean Engineering, 2014, 28(4): 445-456.

[25] 宋辰宁, 周国良, 李小军, 等. 非规则环形圆柱水箱液体晃动动力特性试验[J]. 哈尔滨工程大学学报, 2018, 39(1): 187-192.

SONG Chenning, ZHOU Guoliang, LI Xiaojun, et al. Experiment on sloshing dynamics of irregular annular cylinder water tank[J]. Journal of Harbin Engineering University, 2018, 39(1): 187-192.

[26] 李艳. 基于ADAMS的深海采矿系统联动模拟[J]. 矿山机械, 2006, 34(8): 26-27.

LI Yan. Simulation to the linkage of the mining system in deep ocean on basis of ADAMS[J]. Mining & Processing Equipment, 2006, 34(8): 26-27.

（编辑 赵俊）

收稿日期： 2019 -04 -23; 修回日期： 2019 -07 -08

基金项目(Foundation item)：国家自然科学基金资助项目(51775561)；湖南省自然科学基金资助项目(2018JJ2522) (Project(51775561) supported by the National Natural Science Foundation of China; Project(2018JJ2522) supported by Natural Science Foundation of Hunan Province)

通信作者：杨放琼，博士，教授，从事机械系统动力学研究；E-mail：yangfqcsu@163.com