DOI: 10.11817/j.issn.1672-7207.2020.10.016

含弯头管道超声导波检测
朱龙翔1,赵时2,王悦民3,张海兵1,段刚1
(1. 海军航空大学青岛校区 航空机械工程与指挥系,山东 青岛,266041;
2. 海军航空大学青岛校区 航空装备保障指挥系,山东 青岛,266041;
3. 海军工程大学 动力工程学院,湖北 武汉,433033)
摘要:使用半解析有限元法对弯管中导波传播特性进行研究,计算导波频散曲线和各模态导波的振动特征,并分析两者之间的关系;在ANSYS软件中对L(0,1)模态导波检测含弯头管道进行数值模拟,并使用L(0,1)模态导波对U型管道进行检测实验。研究结果表明:弯管与直管中导波频散曲线的差异与两者中导波振动特征的差异密切相关。在低频条件下,弯管中L(0,1)和T(0,1)模态导波存在截止频率,频散曲线与直管中的差异较大,此时弯管与直管中L(0,1)和T(0,1)模态导波的振动变形差异也较大;随着频率的增加,L(0,1)和T(0,1)模态导波在弯管和直管中振动变形趋于相似,弯管和直管中两者频散曲线也趋于相近。在某些频率范围内,L(0,1)和T(0,1)模态导波与某些弯曲模态导波振动特征类似,此时,在频散曲线中存在“模态耦合”现象;由于弯管不具有轴对称性,弯曲模态导波2个分支的振动特征不再等效,两者的相速度及群速度不再相同,导致频散曲线中存在“模态分支”现象;数值模拟中在截止频率区域和模态耦合区域都出现了较明显的弯头反射信号,弯头反射现象与直管、弯管中频散曲线的差异有关,差异越大,弯头反射越明显;在实际检测中,通过选择合适的频率可以避免弯头反射现象的干扰,有效地对含弯头管道进行检测,且L(0,1)模态导波对于弯头拱腹、拱背处的缺陷具有不同的检测灵敏度。
关键词:导波;含弯头管道;频散曲线;弯头反射;缺陷检测
中图分类号:TB553 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)10-2844-11
Detection of pipeline with elbow using ultrasonic guided wave
ZHU Longxiang1, ZHAO Shi2, WANG Yuemin3, ZHANG Haibing1, DUAN Gang1
(1. Department of Aviation Mechanical and Engineering, Naval Aviation University Qingdao Campus,Qingdao 266041, China;
2. Department of Aviation Equipment Support and Command, Naval Aviation University Qingdao Campus,Qingdao 266041, China;
3. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China)
Abstract: The propagation characteristics of guided waves in pipeline with elbow were studied using semi-analytical finite element method. The dispersion curves and vibration characteristics of guided waves were calculated, and the relationship of them was analyzed. Detecting pipelines with elbow using L(0, 1) mode guided waves was numerically simulated in ANSYS software, and L(0, 1) mode guided waves were used to detect the U-shaped pipeline in experiment. The results show that the dispersion curves differences between elbow and straight pipes are closely related to the vibration characteristics differences. At low frequencies, there are cutoff frequencies for L(0, 1) and T(0, 1) mode guided waves in elbow pipes, and the dispersion curves are significantly different from those in straight pipes. Similarly, the differences between the vibration deformations in elbow and straight pipes are also large. As the frequency increases, the vibration deformations tend to be similar in elbow and straight pipes, and the dispersion curves of both sides tend to be the same. In some frequency ranges, the vibration characteristics of L(0, 1) and T(0, 1) mode are similar to some flexural modes, along with "mode coupling" phenomenon in dispersion curves. As the elbow pipe loses axial symmetry, the vibration characteristics of the two branches of flexural mode guided waves are no longer equivalent, so the phase velocity and group velocity of the two are no longer the same, resulting in "mode branch" phenomenon in dispersion curves. Obvious elbow reflection signals appear in both the cut-off frequency region and the "mode coupling" region in numerical simulation. The elbow reflection phenomenon is related to the difference in the dispersion curves of the straight and elbow pipes. The larger the difference is, the more obvious the elbow reflection is. The pipeline with elbow can be detected effectively in experiment by selecting appropriate frequency as the interference of elbow reflection is avoided, and L(0, 1) mode guided waves have different detection sensitivities for the defects in the intrados and extrados of elbow pipe.
Key words: guided wave; pipeline with elbow; dispersion curves; elbow reflection; defect detection
超声导波具有传播距离远、检测速度快、可覆盖被检测物体的整个横截面、检测效率高等特点,在管道检测中得到了广泛应用。目前,对管道超声导波的研究主要集中在直管,包括各类常见的自由管道、充液管[1]、多层管[2]以及黏弹性材质管[3]。在实际检测中,管道系统主要由直管和弯管组成,在工程应用中,常需要检测带有弯头的管道系统。管道中弯头的存在,影响了导波在管道中的传播,对管道检测造成不利的影响。与直管不同,在弯管所处的环形坐标系下无法通过传统的解析法得到导波的频散方程,只能通过数值方法来进行求解。DEMMA等[4-5]使用模态分析方法对弯管中导波频散曲线进行了分析,然而,该方法只能计算一些离散的数据点,无法满足工程应用的需要。HAYASHI等[6]首次用半解析有限元法推导了弯管中导波传播的特征值方程,然而没有对弯管中导波的频散特性进行深入研究。目前,对弯管的研究多集中于数值模拟与实验研究[7-17],理论研究较为缺乏。伍文君等[18]使用半解析有限元法对弯管中导波频散曲线进行了计算,利用L(0,1)模态导波对含弯头管道进行了实验研究,发现在检测中存在弯头反射现象,但没有结合理论计算结果对实验现象进行深入探讨。由于在舰船管道系统中存在许多小口径带弯头管道,本文作者使用半解析有限元法对小口径弯管中导波传播特性进行分析,结合理论分析、仿真实验研究弯头对导波检测的影响。
1 半解析有限元法
为了有效地描述弯管中各质点的坐标,引入环形坐标系,如图1所示。
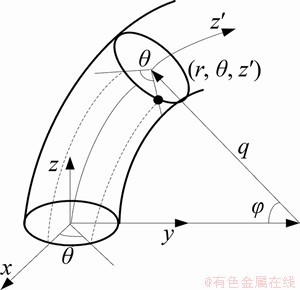
图1 环形坐标系
Fig. 1 Toroidal coordinate
环形坐标系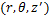 与直角坐标系
与直角坐标系 之间的几何关系为[6]
之间的几何关系为[6]
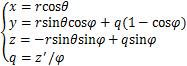 (1)
(1)
式中: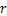 和
和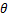 分别为弯管中某点在该截面处的极径和极角,
分别为弯管中某点在该截面处的极径和极角,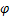 为弯管中某点所在截面对应的弯曲角度,
为弯管中某点所在截面对应的弯曲角度,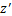 为弯管中某点所在截面圆心对应的弯曲弧长,
为弯管中某点所在截面圆心对应的弯曲弧长,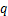 为弯管截面圆心处的弯曲半径。
为弯管截面圆心处的弯曲半径。
在环形坐标系中,弯管中任一质点的位移矢量 、应变矢量
、应变矢量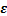 、应力矢量
、应力矢量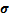 分别为:
分别为:
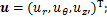
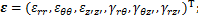
 (2)
(2)
导波在弯管中传播时,其传播方向沿轴向方向(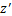 方向),管道所受的外力(体力、面力)为0,由虚功原理可以推出其动力学控制方程[5]为
方向),管道所受的外力(体力、面力)为0,由虚功原理可以推出其动力学控制方程[5]为
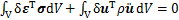 (3)
(3)
式中: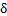 为变分符号,
为变分符号,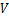 为体积,
为体积,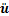 为
为 对时间的二阶偏导数,
对时间的二阶偏导数, 为密度。根据导波传播特点,管道中任意一点的位移矢量
为密度。根据导波传播特点,管道中任意一点的位移矢量 可写为
可写为
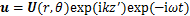 (4)
(4)
式中: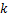 为波数,
为波数, 为角频率,
为角频率,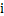 为虚数单位,
为虚数单位,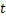 为时间,
为时间,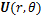 为与
为与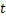 和
和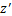 无关的矢量,其取值仅与坐标
无关的矢量,其取值仅与坐标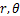 有关。将式(4)代入式(3),结合环形坐标系下弹性力学几何方程及物理方程,可将三维体积分计算转化为对弯管截面的二维面积分,通过对弯管截面进行有限元离散,可以得到弯管中导波频散方程为
有关。将式(4)代入式(3),结合环形坐标系下弹性力学几何方程及物理方程,可将三维体积分计算转化为对弯管截面的二维面积分,通过对弯管截面进行有限元离散,可以得到弯管中导波频散方程为
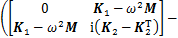
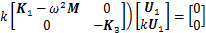 (5)
(5)
式中: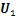 为截面内所有节点的位移向量;
为截面内所有节点的位移向量;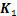 ,
,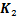 ,
, 和
和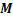 为截面的整体矩阵。给定一个角频率
为截面的整体矩阵。给定一个角频率 ,通过求解特征值可得到一组波数
,通过求解特征值可得到一组波数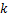 ,每对
,每对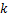 -
- 对应一种导波模态,根据
对应一种导波模态,根据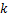 -
- 之间的关系,可对频散曲线进行计算。
之间的关系,可对频散曲线进行计算。
2 频散曲线计算
使用等参数四边形单元对弯管截面进行离散,如图2所示,将弯管截面划分为128个单元,周向64个单元,径向2个单元。弯管的材质为钢,密度为7 932 kg/m3,弹性模量为217 GPa,泊松比为0.3。管道的外径为28 mm,壁厚为3 mm。弯管的弯曲半径q取不同值,使用matlab软件进行编程,对导波的频散曲线进行计算。
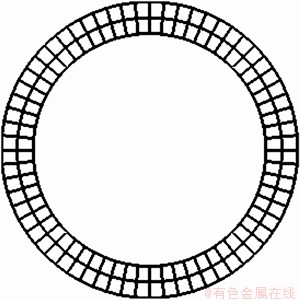
图2 截面网格划分示意图
Fig. 2 Diagram of cross-section with finite element meshes
图3~6所示为计算得到的导波群速度频散曲线,其中图3所示为直管(弯曲半径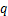 取无穷大)的计算结果,图4~6所示为弯管(弯曲半径分别为280,140和70 mm)的计算结果。对比可发现弯管中导波频散曲线有以下特点:1) 弯管中L(0,1)和T(0,1)模态存在截止频率,且随着弯曲半径减小,截止频率逐渐增大。2) T(0,1)模态的群速度不再保持恒定。3) 弯管中弯曲模态的群速度曲线出现了“模态分支”现象(群速度曲线存在2个分支,如图4~6中圆形标记所示)。4) 弯管中群速度曲线存在“模态耦合”现象(群速度曲线在某些频率区域存在突变,如图4~6中矩形标记所示)。这些结果与文献[18]中的计算结果一致。
取无穷大)的计算结果,图4~6所示为弯管(弯曲半径分别为280,140和70 mm)的计算结果。对比可发现弯管中导波频散曲线有以下特点:1) 弯管中L(0,1)和T(0,1)模态存在截止频率,且随着弯曲半径减小,截止频率逐渐增大。2) T(0,1)模态的群速度不再保持恒定。3) 弯管中弯曲模态的群速度曲线出现了“模态分支”现象(群速度曲线存在2个分支,如图4~6中圆形标记所示)。4) 弯管中群速度曲线存在“模态耦合”现象(群速度曲线在某些频率区域存在突变,如图4~6中矩形标记所示)。这些结果与文献[18]中的计算结果一致。
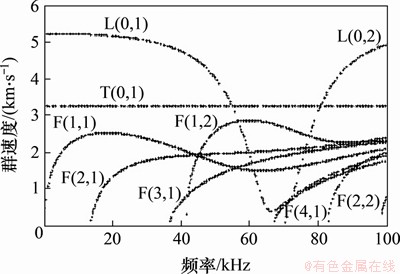
图3 群速度频散曲线(q为无穷大)
Fig. 3 Group velocity dispersion curves(q is infinite)
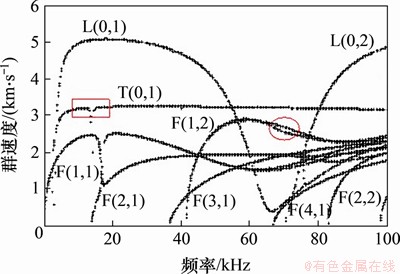
图4 群速度频散曲线(q=280 mm)
Fig. 4 Group velocity dispersion curves(q=280 mm)
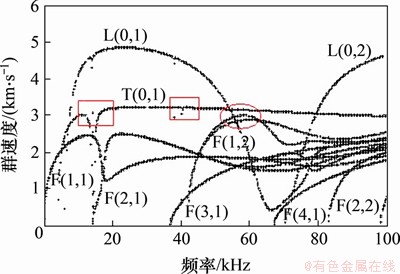
图5 群速度频散曲线(q=140 mm)
Fig. 5 Group velocity dispersion curves(q=140 mm)
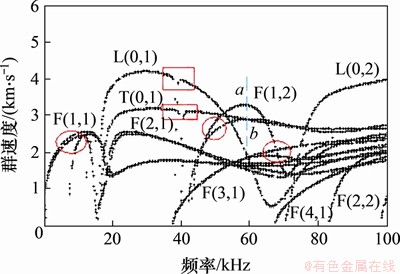
图6 群速度频散曲线(q=70 mm)
Fig. 6 Group velocity dispersion curves(q=70 mm)
3 模态特征分析
特征值方程(式(5))中的每一组 -
- 都对应着导波的某种模态,且此时的特征向量为该模态导波传播时横截面上各节点的位移。根据各节点的位移,代入各单元的形函数,即可得到横截面上各点的位移分布,进而得到各模态导波的振动模态特征。图7所示为直管(弯曲半径无限大)中各模态导波所导致的截面振动变形示意图,其中,粗线所绘制的圆截面表示变形前的截面,细线表示变形后的截面。从图7可以看到:在直管中L(0,1)模态的截面变形为沿半径方向发生轴对称伸缩;T(0,1)模态的截面变形为轴对称扭转变形;F(1,1)模态的截面变形主要相对原位置发生了平动;F(2,1)模态和F(3,1)模态的截面变形具有与导波周向阶数相同的凸点和凹点,其中,F(2,1)模态下的凸点、凹点数为2个,F(3,1)模态下的凸点、凹点数为3个,且各凸点、凹点分别关于截面圆心轴对称分布。
都对应着导波的某种模态,且此时的特征向量为该模态导波传播时横截面上各节点的位移。根据各节点的位移,代入各单元的形函数,即可得到横截面上各点的位移分布,进而得到各模态导波的振动模态特征。图7所示为直管(弯曲半径无限大)中各模态导波所导致的截面振动变形示意图,其中,粗线所绘制的圆截面表示变形前的截面,细线表示变形后的截面。从图7可以看到:在直管中L(0,1)模态的截面变形为沿半径方向发生轴对称伸缩;T(0,1)模态的截面变形为轴对称扭转变形;F(1,1)模态的截面变形主要相对原位置发生了平动;F(2,1)模态和F(3,1)模态的截面变形具有与导波周向阶数相同的凸点和凹点,其中,F(2,1)模态下的凸点、凹点数为2个,F(3,1)模态下的凸点、凹点数为3个,且各凸点、凹点分别关于截面圆心轴对称分布。
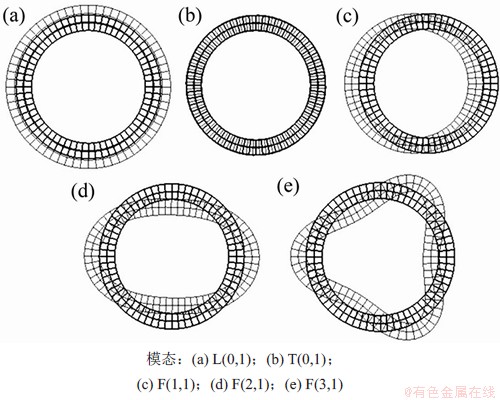
图7 直管中各模态导波下的截面变形图(f=40kHz)
Fig. 7 Deformed shapes of the cross-section for different modes in straight pipe(f=40 kHz)
图8和图9所示为弯管中L(0,1)和T(0,1)模态下截面变形示意图,图中的箭头方向指向弯管的弯曲圆心。从图8和图9可以看到:与直管中的轴对称变形状态不同,弯管中L(0,1)模态下截面沿着管道弯曲方向进行伸缩及平动,T(0,1)模态下截面沿与管道弯曲方向近似垂直方向进行平动及伸缩。将图8、图9与图7进行比较可知:在低频条件下,弯管中L(0,1)和T(0,1)模态导波的模态特征呈现出直管中F(1,1)模态的特征,而随着频率增加,弯管中L(0,1)和T(0,1)模态导波截面变形越来越趋于轴对称性,与直管中的L(0,1)和T(0,1)模态特征趋于相似。
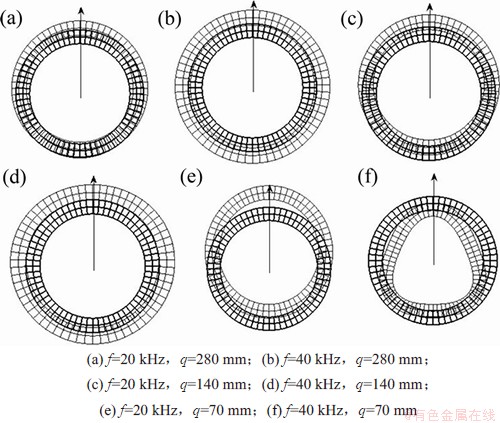
图8 弯管中L(0,1)模态下截面变形图
Fig. 8 Deformed shapes of the cross-section for L(0,1) mode in curved pipe
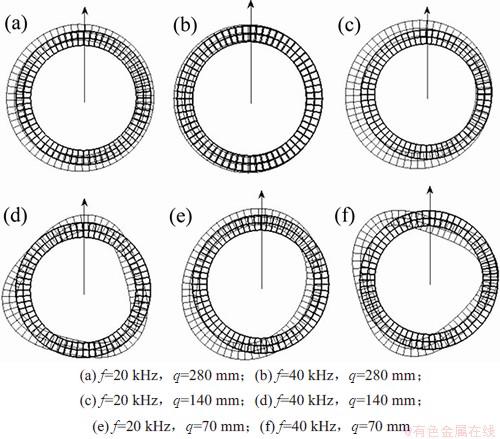
图9 弯管中T(0,1)模态下截面变形图
Fig. 9 Deformed shapes of the cross-section for T(0,1) mode in curved pipe
上述现象与图3~6中频散曲线是一致的,即在低频状态,弯管中L(0,1)和T(0,1)模态的频散曲线与直管中差异较大,畸变较明显,而随着频率的增加,弯管中L(0,1)和T(0,1)模态的频散曲线与直管中趋于相同。值得注意的是,在图8(f)、图9(d)、图9(f)中,L(0,1)和T(0,1)模态出现了类似直管中F(3,1)模态的特征,通过对比该频率(f=40 kHz)时弯管中F(3,1)模态的特征可以发现,双方有较大的相似性(如图10所示),而观察图5和图6可知,频率40 kHz附近区域正好是L(0,1),T(0,1)模态与F(3,1)模态存在模态耦合现象的频率区域。同样,对图4和图5中T(0,1)模态与F(2,1)模态的模态耦合区域(频率15 kHz附近)进行分析,此时T(0,1)模态的截面变形图与F(2,1)模态的截面变形图相近(见图11和图12)。可以推测,由于相关导波模态振动特征相类似,导致了频散曲线中模态耦合现象产生。
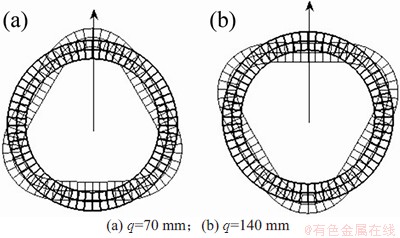
图10 弯管中F(3,1)模态下截面变形图(f=40 kHz)
Fig. 10 Deformed shapes of the cross-section for F(3,1) mode in curved pipe(f=40 kHz)
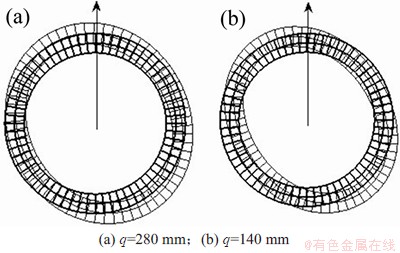
图11 弯管中T(0,1)模态下截面变形图(f=15 kHz)
Fig. 11 Deformed shapes of the cross-section for T(0,1) mode in curved pipe(f=15 kHz)
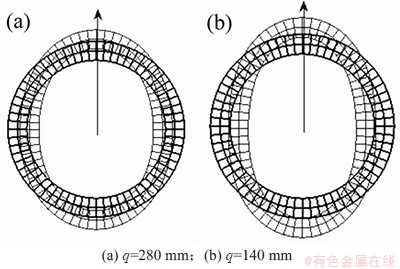
图12 弯管中F(2,1)模态下截面变形图(f=15 kHz)
Fig. 12 Deformed shapes of the cross-section for F(2,1) mode in curved pipe(f=15 kHz)
对图6中F(1,2)模态的2个分支进行分析,计算频率为60 kHz时(即图6中所示的a和b点)的截面变形示意图,如图13所示。从图13可见:对于F(1,2)模态而言,a点所在分支对应的截面变形方向与弯管的弯曲方向平行,而b点所在分支对应的截面变形方向与弯管的弯曲方向垂直。在直管中,由于直管的轴对称性,F(1,2)模态的2个分支的截面变形特征是等效的,具有相同的相速度与群速度[5];而在弯管中,由于弯曲方向的存在,弯管不再具有轴对称性,F(1,2)模态的2个分支不再等效,两者的相速度及群速度不再相同,因此,导致频散曲线中“模态分支”现象的产生。
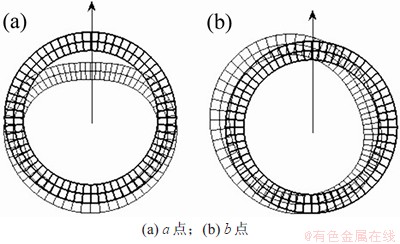
图13 弯管中F(1,2)模态下截面变形图(f=60 kHz)
Fig. 13 Deformed shapes of the cross-section for F(1,2) mode in curved pipe(f=60 kHz)
4 数值模拟
在实际的管道系统中,很少存在弯曲半径恒定的弯曲管道,最常见的是由直管和弯头共同组成的含弯头管道。使用ANSYS软件对含弯头的管道进行数值模拟,管道的轴线长度为2.4 m,外径为28 mm,壁厚为3 mm。管道材质与前面的相同。管道由长直管、弯头、短直管组成,弯头的弯曲角度为90o,弯头的中心位于管道总长度的2/3即1.8 m处,如图14所示。使用solid164单元对管道进行扫掠网格划分,单元沿轴向方向的长度设为2 mm,沿管道圆周方向的单元数为24个。通过对长直管的端部各节点分别施加轴向位移载荷(载荷信号为经汉宁窗调制的信号),可以对纵向导波进行模拟激励,通过对长直管端部附近节点的轴向位移进行监测,可以模拟对导波信号进行接收。由图3中的频散曲线可知,低频区域在长直管中产生的纵向导波为L(0,1)模态导波。改变弯头的半径(分别为280,140和70 mm),建立不同的管道模型进行分析。图15~17所示为不同弯头半径下管道的模拟检测信号。
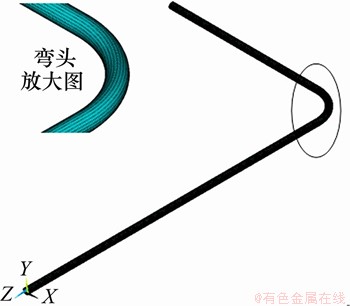
图14 管道模型图
Fig. 14 Pipe model
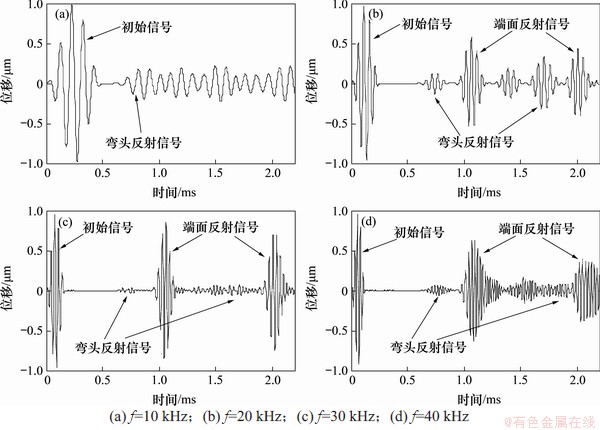
图15 L(0,1)模态导波数值模拟信号(q=70 mm)
Fig. 15 L(0,1) mode guided wave signals in numerical simulation(q=70 mm)
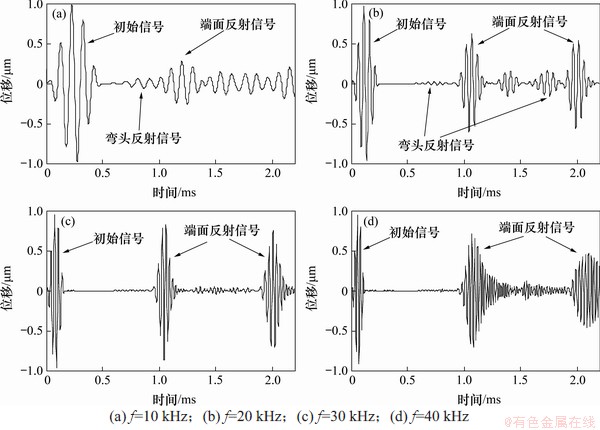
图16 L(0,1)模态导波数值模拟信号(q=140 mm)
Fig. 16 L(0,1) mode guided wave signals in numerical simulation(q=140 mm)
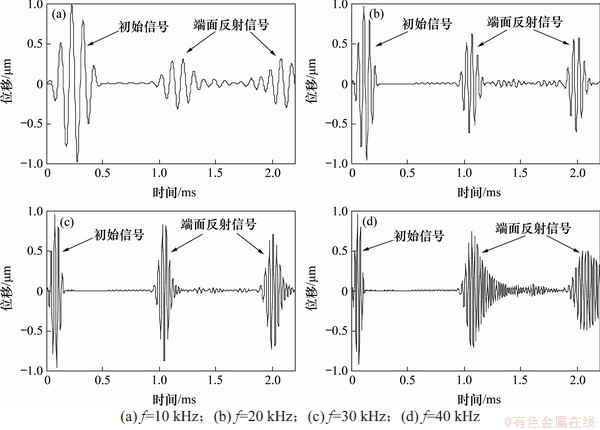
图17 L(0,1)模态导波数值模拟信号(q=280 mm)
Fig. 17 L(0,1) mode guided wave signals in numerical simulation(q=280 mm)
当L(0,1)模态导波在长直管中被激励出来后,此时将按照直管中L(0,1)模态导波的特点传播;进入弯头区域后,将按照弯管中L(0,1)模态导波的特点传播;进入短直管后,又将按照直管中L(0,1)模态导波的特点传播,如此循环往复[4]。图15所示为q=70 mm时接收到的L(0,1)模态导波信号,可以看到当f=10 kHz时,在0.68 ms左右出现了第1次反射回波。根据直管中L(0,1)模态导波信号在该频率下的群速度(5 214 m/s),计算得到产生反射信号的位置应该在距激励端1.77 m左右,可知该反射信号为弯头的反射信号。在弯头反射信号之后,信号比较杂乱,无法识别出管道端面的反射信号。当f=20 kHz时,在弯头反射信号之后出现了明显的波包信号(该波包的波前在时间t=0.95 ms处),考虑到此时弯头的长度相对直管很小,用直管中L(0,1)模态导波信号在该频率下的群速度(5 156 m/s)进行近似计算,可得该反射信号的位置距激励端约为2.4 m,可以确认该信号为管道另一端面的第1次反射信号。图15(b)中在第1、第2次端面反射信号之间出现了与弯头反射信号对应的波包信号,该信号与第2次弯头反射信号关于2次端面反射信号的中心位置对称,且第2次弯头反射信号比第1次反射信号有所增强,该现象是由导波在管道中来回传播并反射造成的[19]。
对比图15~17可以发现,当q=70 mm时,在弯头处都发生了反射信号,且随着频率的增加,弯头反射信号整体呈下降趋势;当q=140 mm,频率较低时,弯头处具有反射信号,而在频率较高时,反射信号基本上消失;当q=280 mm时,在弯头处基本上看不到反射信号,上述结果与文献[18]中的实验结果类似。结合图3~6中频散曲线可以发现,当q=280 mm时,L(0,1)模态导波的截止频率非常小,在10~40 kHz范围内弯管中频散曲线与直管中的差异很小,基本相同;当q=140mm时,L(0,1)模态导波的截止频率约为7 kHz,在10~20 kHz范围内,弯管中频散曲线与直管中的差异较大,在30~40 kHz范围内差异很小;当q=70 mm时,L(0,1)模态导波的截止频率约为15 kHz,在10~20 kHz范围内,弯管中频散曲线与直管中的差异很大,在30~40 kHz范围内差异较小。可见,当弯管中导波频散曲线与直管中的存在差异时,会在弯头处产生反射,差异越大,反射越明显。因此,当频率小于截止频率或在截止频率附近时,会发生明显的弯头反射现象。由前面的分析可知,弯管与直管中导波的模态振型差异和频散曲线差异密切相关,这也意味着弯管与直管中导波的模态振型差异越大,弯头反射越大,这与文献[13]中的研究结果相吻合,但文献[13]仅仅分析了各模态的振型,缺少频散曲线的验证。
从图15可知:当q=70 mm时,L(0,1)模态导波截止频率为15 kHz左右,这意味着在10 kHz时,弯管中不存在L(0,1)模态导波,当直管中L(0,1)模态导波传播到弯管中时,相当大的能量被反射回来,另一部分将进行模态转换,即以弯管中振动形式相近的F(1,1)模态进行传播[5],因此,到达短直管端面并被反射回来的L(0,1)模态导波能量很小,在图中无法观察到明显的端面反射回波信号,而且各类反射回波叠加到一起,在弯头第一次反射回波后产生了一系列杂波信号;当f=40 kHz时,弯头反射信号比f=30 kHz时更为强烈,该现象可以认为是模态耦合现象的一种反映,由前文可知当f为40 kHz左右时L(0,1)模态与F(3,1)模态存在模态耦合现象,由于该频率附近的频散曲线与直管中差异较大,与f=30 kHz时相比,更多的能量被反射回来,弯头反射信号有所增强。
5 实验研究
使用基于磁致伸缩效应的导波传感器[20]对U型管进行检测。U型管由2段直管和1段180o弯管组成,弯管部分的弯曲半径为R=192.5 mm,2段直管的长度都为L=1 290 mm,管道的外径d=28 mm,管壁厚度为h=3 mm。U型管的材料为碳钢,材料参数与前文的相同。图18所示为实验装置示意图。传感器分为激励传感器和接收传感器,分别由激励线圈和接收线圈组成,对激励线圈施加交变电流,可以通过磁致伸缩效应在U型管(见图19)中产生纵向超声导波,并由逆磁致伸缩效应对导波信号进行接收。磁化线圈用来提供偏置磁场,偏置磁场的存在可以提高传感器的灵敏度。实验中,激励传感器和接收传感器都放置在图19中A端,且两者相距很近,这种配置使得激励的导波相当于在管道中一端入射,同端激励,同端接收。根据直管部分导波频散曲线(见图3)可知,低频区域在长直管中产生的纵向导波为L(0,1)模态导波。图20所示为频率为30 kHz时完整U型管道实验检测信号,信号中最左侧的波包为初始激励信号,后续的波包为端面反射回波信号,根据各端面回波的时间间隔,可以计算出L(0,1)模态导波在整个U型管中传播的平均速度。表1所示为实验得到的平均速度与直管、弯管中理论速度之间的关系,由于弯管中L(0,1)模态导波的理论速度普遍要稍低于直管中的理论速度,因此,整体的实验平均速度介于直管和弯管中的理论速度之间。
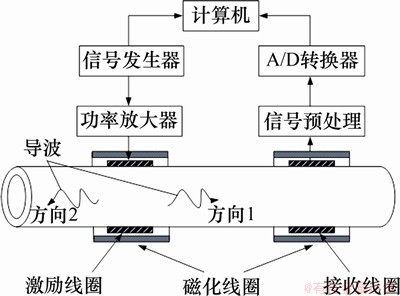
图18 实验装置示意图
Fig. 18 Schematic diagram of the experimental setup

图19 实验用U型管
Fig. 19 U-shaped pipeline in experiment
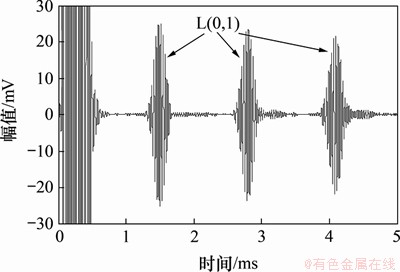
图20 完整U型管实验检测信号(f=30 kHz)
Fig. 20 Detection signals for intact U-shaped pipeline (f=30 kHz)
表1 L(0,1)模态导波传播速度
Table 1 Velocity of L(0,1) mode guided wave
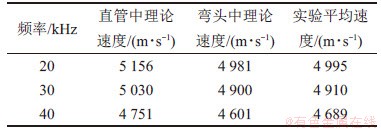
图21所示为弯头处导波的频散曲线,与直管处导波的频散曲线(图3)相比,由于在频率大于20 kHz时L(0,1)频散曲线基本接近,而且在20~40 kHz频率区域L(0,1)既不存在截止频率也没有模态耦合现象,因此,图20中没有发现明显的弯头反射信号,使用该频率范围进行检测时,可以避开弯头反射的干扰,保证检测效果。在U型管道弯头中间部位加工刻痕缺陷,刻痕的宽度为2 mm、长度为16 mm,位于弯头中心位置的拱腹处,对其进行检测实验。图22所示为频率为30 kHz时,缺陷位于拱腹处的检测信号,可见在相临的端面反射回波的正中间出现了明显的缺陷反射信号,说明L(0,1)模态导波可以有效地对弯头中的缺陷进行检测。
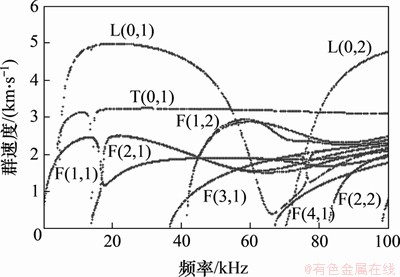
图21 U型管的弯头中导波频散曲线
Fig. 21 Dispersion curves of elbow part in U-shaped pipeline
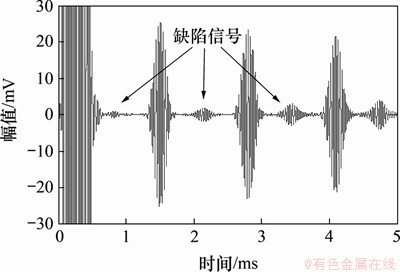
图22 缺陷位于拱腹处的检测信号
Fig. 22 Detection signals for the defect in intrados
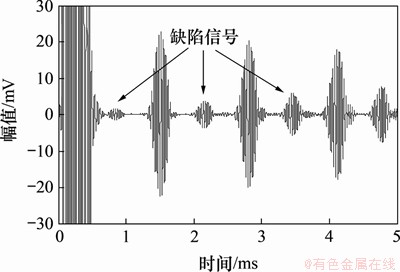
图23 缺陷位于拱背处的检测信号
Fig. 23 Detection signals for the defect in extrados
取另一根相同的U型管道,弯头中间部位加工同样大小的刻痕缺陷,但刻痕位于弯头中心位置的拱背处,频率为30 kHz时的检测信号如图23所示。经对比可知,对于同样大小的缺陷,当缺陷位于弯头不同的周向位置时,其反射信号的幅值不一样,拱背处缺陷的反射信号幅值要明显大于拱腹处缺陷的反射信号幅值。可见在弯管检测中,L(0,1)模态导波对于拱腹处和拱背处的缺陷具有不同的检测灵敏度,在缺陷判定时要注意加以辨别。
6 结论
1) 弯管中导波频散曲线的特征与导波的振动特征密切相关。在低频条件下,弯管中L(0,1)和T(0,1)模态导波的模态特征与直管中的相比具有较大的差异,随着频率增加,两者趋于相似。与之对应,在低频状态时,弯管中L(0,1)和T(0,1)模态的频散曲线与直管中的差异较大,存在截止频率,而随着频率增加,弯管中L(0,1)和T(0,1)模态的频散曲线与直管中的趋于相同。弯管中频散曲线中存在“模态耦合”和“模态分支”现象,“模态耦合”处L(0,1)和T(0,1)模态导波与相关弯曲模态导波的振动特征相类似,弯曲模态导波2个“模态分支”的振动特征丧失了等效性,具有不同的传播速度。
2) 通过对含弯头管道进行数值模拟发现,当弯管中导波频散曲线与直管中的存在差异时,L(0,1)模态导波会在弯头处产生反射,差异越大,反射越明显。因此,当频率小于截止频率或在截止频率附近以及位于模态耦合频率区域时,会产生明显的弯头反射信号,对管道检测造成不利影响。
3) 使用L(0,1)模态导波进行检测时,通过选择合适的频率可以避免弯头反射现象的干扰,有效检测出含弯头管道中的缺陷,且L(0,1)模态导波对于弯头拱腹、拱背处的缺陷具有不同的检测灵敏度。
参考文献:
[1] MAZZOTTI M, MINIACI M, BARTOLI I. A numerical method for modeling ultrasonic guided waves in thin-walled waveguides coupled to fluids[J]. Computers and Structures, 2019, 212:248-256.
[2] 张小伟, 唐志峰, 吕福在, 等. 基于半解析有限元法的多层管超声导波数值模拟与试验研究[J]. 机械工程学报, 2014, 50(8): 10-16.
ZHANG Xiaowei, TANG Zhifeng, LU Fuzai, et al. Numerical simulation and experimental investigation on ultrasonic guided waves in multilayered pipes based on SAFE[J]. Journal of Mechanical Engineering, 2014, 50(8): 10-16.
[3] BAUSE F, GRAVENKAMP H, RAUTENBERG J, et al. Transient modeling of ultrasonic guided waves in circular viscoelastic waveguides for inverse material characterization[J]. Measurement Science and Technology, 2015, 26(9): 095602.
[4] DEMMA A, CAWLEY P, LOWE M J S. Guided waves in curved pipes[J]. Review of Quantitative Nondestructive Evaluation, 2002, 21: 157-164.
[5] DEMMA A, CAWLEY P, LOWE M J S, et al. The effect of bends on the propagation of guided waves in pipes[J]. Journal of Pressure Vessel Technology, 2005, 127: 328-335.
[6] HAYASHI T, KAWASHIMA K, SUN Z Q, et al. Guided wave propagation mechanics across a pipe elbow[J]. Journal of Pressure Vessel Technology, 2005, 127: 322-327.
[7] MIKI M, NAGASHIMA Y, ENDOU M, et al. Evaluation for defect detection over bending zone in piping by guided wave[J]. Review of Quantitative Nondestructive Evaluation, 2010, 29: 111-117.
[8] VERMA B, MISHRA T K, BALASUBRAMANIAM K, et al. Interaction of low-frequency axisymmetric ultrasonic guided waves with bends in pipes of arbitrary bend angle and general bend radius[J]. Ultrasonics, 2014, 54: 801-808.
[9] EL BAKKALI M, LHEMERY A, BARONIAN V, et al. A modal formulation for the propagation of guided waves in straight and curved pipes and the scattering at their junction[J]. Journal of Physics: Conference Series, 2014, 498: 012012.
[10] PARK J, LEE J, JEONG S G, et al. A study on guided wave propagation in a long distance curved pipe[J]. Journal of Mechanical Science and Technology, 2019, 33(9): 4111-4117.
[11] QI M X, ZHANG P G, NI J, et al. Experiment and numerical simulation of ultrasonic guided wave propagation in bent pipe[J]. Procedia Engineering, 2015, 130: 1603-1611.
[12] QI M X, ZHOU S P, NI J, et al. Investigation on ultrasonic guided waves propagation in elbow pipe[J]. International Journal of Pressure Vessels and Piping, 2016, 139/140: 250-255.
[13] 耿海泉, 王悦民, 邓文力, 等. 基于模态置信准则计算的L(0,1)导波弯头反射研究[J]. 中国科学: 技术科学, 2017, 47(12): 1295-1303.
GENG Haiquan, WANG Yuemin, DENG Wenli, et al. Research on reflection of L(0,1) guided wave from pipe elbow based on modal assurance criteria calculation[J]. Scientia Sinica Technologica., 2017, 47(12): 1295-1303.
[14] 耿海泉, 王悦民, 陈乐, 等. 磁致伸缩扭转导波小管径弯管检测[J]. 国防科技大学学报, 2018, 40(1): 168-175.
GENG Haiquan, WANG Yuemin, CHEN Le, et al. Inspection of small diameter bending pipes using magnetostrictive torsional guided wave[J]. Journal of National University of Defense Technology, 2018, 40(1): 168-175.
[15] 周邵萍, 张蒲根, 吕文超, 等. 基于导波的弯管裂纹缺陷的检测[J]. 机械工程学报,2015, 51(6): 58-65.
ZHOU Shaoping, ZHANG Pugen, LV Wen-chao, et al. Detection of cracks in elbow pipes using guided waves[J]. Journal of Mechanical Engineering, 2015, 51(6): 58-65.
[16] 李阳, 邹云, 张双楠, 等. T(0,1)模态导波在弯管上传播的仿真与实验[J], 声学技术,2017, 36(5): 442-449.
LI Yang, ZOU Yun, ZHANG Shuangnan, et al. Numerical and experimental research on T(0,1) guided waves propagating in bended pipes[J], Technical Acoustics, 2017, 36(5): 442-449.
[17] 罗更生, 谭建平, 卢超, 等. L(0,2)模态导波检测弯管缺陷的数值模拟和实验研究[J]. 中南大学学报(自然科学版),2014, 45(9): 3029-3036.
LUO Gengsheng, TAN Jianping, LU Chao, et al. Numerical simulation and testing research for defect detection in bend pipes using longitudinal mode L(0,2)[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3029-3036.
[18] 伍文君, 王悦民, 陈乐, 等. 管道弯头对低频纵向导波传播特性影响分析[J]. 声学学报, 2017, 42(1): 95-102.
WU Wenjun, WANG Yuemin, CHEN Le, et al. The effect of pipe bend on low-frequency longitudinal mode guided wave propagation[J]. Acta Acustica, 2017, 42(1): 95-102.
[19] 朱龙翔, 王悦民, 孙丰瑞. 磁致伸缩扭转导波管道缺陷检测数值模拟和实验研究[J]. 中南大学学报(自然科学版), 2014, 45(9): 3001-3007.
ZHU Longxiang, WANG Yuemin, SUN Fengrui. Numerical simulation and experimental study on detecting defects in pipes using magnetostrictive T(0,1) mode guided wave[J]. Journal of Central South University(Science and Technology), 2014, 45(9): 3001-3007.
[20] 王悦民, 康宜华, 武新军. 基于磁致伸缩效应的钢管缺陷检测实验研究[J]. 振动测试与诊断, 2004, 24(3): 210-213.
WANG Yuemin, KANG Yihua, WU Xinjun. A technique of nondestructive inspection of steel pipes based on magnetostrictive effect[J]. Journal of Vibration, Measurement & Diagnosis, 2004, 24(3): 210-213.
(编辑 伍锦花)
收稿日期: 2019 -11 -29; 修回日期: 2020 -02 -03
基金项目(Foundation item):国防预研基金资助项目(9140A27020115JB11070) (Project(9140A27020115JB11070) supported by the Defense Research Foundation)
通信作者:朱龙翔,博士,讲师,从事超声导波无损检测研究;E-mail: jdyzzlx@126.com