J. Cent. South Univ. (2012) 19: 1859-1868 

DOI: 10.1007/s11771-012-1220-1

Nonlinear trajectory tracking control of a new autonomous underwater vehicle in complex sea conditions

GAO Fu-dong(高富东)¹, PAN Cun-yun(潘存云)¹, HAN Yan-yan(韩艳艳)², ZHANG Xiang(张湘)¹

1. College of Mechatronic Engineering and Automation,

National University of Defense Technology, Changsha 410073, China;

2. SANY Heavy Industry Co. Ltd, Changsha 410100, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: Autonomous underwater vehicles (AUVs) navigating in complex sea conditions usually require a strong control system to keep the fastness and stability. The nonlinear trajectory tracking control system of a new AUV in complex sea conditions was presented. According to the theory of submarines, the six-DOF kinematic and dynamic models were decomposed into two mutually non-coupled vertical and horizontal plane subsystems. Then, different sliding mode control algorithms were used to study the trajectory tracking control. Because the yaw angle and yaw angle rate rather than the displacement of the new AUV can be measured directly on the horizontal plane, the sliding mode control algorithm combining cross track error method and line of sight method was used to fulfill its high-precision trajectory tracking control in the complex sea conditions. As the vertical displacement of the new AUV can be measured, in order to achieve the tracking of time-varying depth signal, a stable sliding mode controller was designed based on the single-input multi-state system, which took into account the characteristic of the hydroplane and the amplitude and rate constraints of the hydroplane angle. Moreover, the application of dynamic boundary layer can improve the robustness and control accuracy of the system. The computational results show that the designed sliding mode control systems of the horizontal and vertical planes can ensure the trajectory tracking performance and accuracy of the new AUV in complex sea conditions. The impacts of currents and waves on the sliding mode controller of the new AUV were analyzed qualitatively and quantitatively by comparing the trajectory tracking performance of the new AUV in different sea conditions, which provides an effective theoretical guidance and technical support for the control system design of the new AUV in real complex environment.

Key words: complex sea condition; autonomous underwater vehicle (AUV); trajectory tracking; sliding mode control

1 Introduction

Autonomous underwater vehicles (AUVs) are promising vehicles for navy use because they can fulfill many missions such as assaults, communications and obviating torpedoes. In order to meet the needs of future high-tech naval warfare, fastness and seakeeping of the AUVs become the basic premise of safe navigation and effective use of weapons. The multi-moving state AUV in this work makes use of the flexible transmission shaft based on spherical gear as the kinetic source equipment [1], on the end of which a new wheel propeller is installed. The whole equipment can achieve four functions such as wheels, legs, thrusters and course control based on the characteristics of spatial deflexion and continual circumgyratetion of the flexible transmission shaft. The rudders and vectored thrusters are used to control the course at high speed and low speed, respectively. The typical motions of the AUV are shown in Fig. 1 [2]. As AUVs are subjected to the larger interference effect from underwater environment, in order to ensure the stability of the new AUV, it needs a good control system with strong robustness and anti-jamming capability. However, the new AUV is a highly non-linear, time-varying and strong coupling system. Taking into account the uncertainty of environmental interference, it is difficult to establish an accurate motion model. Therefore, the control method used by the new AUV should get rid of the dependence on the precise mathematical model. The nonlinear trajectory tracking control of the AUVs in complex sea conditions has been a key issue in AUV design which is also concerned by AUV designers. So, it has important theoretical and practical significance to study this issue.

Among many control methods, sliding mode control has strong robustness about parameters change, uncertainties and external disturbances of the system, so sliding mode control is very effective to solve the control problem of the AUVs in complex sea conditions. Currently, scholars mainly study sliding mode control based on simplified kinematic and dynamic models of the AUV in the case of non-environmental interference [3-5]. The simplified models ignore the impacts of some important factors on the AUV movements, such as the high order damping term, and the second order of some velocity component, etc., which makes the control failures often occur in practical applications of the designed control systems. The trajectory tracking control of the AUV on the horizontal plane is more complicated compared with that on the vertical plane, because the displacement of the AUV on the horizontal plane cannot be measured directly, which leads to the trajectory tracking in the horizontal plane carried out only through the measurements of yaw angle and yaw angle rate. In the horizontal trajectory tracking control algorithm, a sliding mode control algorithm based on the line of sight method has been proposed [6-7], which achieves trajectory tracking through reducing the error of yaw angle continually. But this method cannot guarantee the tracking error to a minimum, which is a low-precision sliding mode control algorithm. Cross trajectory error method can effectively reduce trajectory tracking error, which is a high-precision method. But the method is difficult to guarantee the stability of the system in the case of larger course deviation [8]. In order to design a sliding mode controller that can meet the requirements of control system in complex sea conditions with low tracking error and high stability, a sliding mode controller combining cross track error method and line of sight method based on the full six-DOF non-linear kinematic and dynamic models was designed for the horizontal trajectory tracking control of new AUV. Moreover, a stable sliding mode controller based on the dynamic boundary layer was designed for depth tracking control on the vertical plane where the vertical displacement can be measured.

Fig. 1 Typical motions of vectored thruster AUV: (a) Cruising forward; (b) Vertical descend; (c) Transverse turning; (d) Wheeled moving or transverse pushing; (e) Landing sea-bottom or vertical ascending; (f) Pivot steering or crawling on sea-bottom

2 Six-DOF nonlinear dynamic model of new AUV in complex sea conditions

Many parameters of the new AUV need to be identified in the complex sea conditions, because it is a complicated nonlinear dynamic system. In order to describe the movement of the new AUV, the inertial coordinate system E-ξηζ and body-fixed coordinate system B-xyz are used, as shown in Fig. 2. The origin B of body-fixed coordinate system is 0.003 m from the center of buoyancy. The new AUV has two symmetry planes and the body’s symmetry axes coincide with the principal axes of inertia, so the inertia tensor in the body-fixed coordinate system is diagonal. The kinematic parameters include η that denotes the position and attitude vector in the inertial coordinate system, v that denotes the linear and angular velocity vector in the body-fixed coordinate system and f that describes the forces and moments acting on the vehicle in the body-fixed coordinate system. The specific forms can be written as follows:

, η₁=(ξ, η, ζ)^T, η₂=(f, θ, ψ)^T;

, v₁=(u, v, w)^T, v₂=(p, q, r)^T;

,  f₁=(X, Y, Z)^T,  f₂=(K, M, N)^T

where η₁ is the position vector, η₂ is the attitude vector, v₁ is the linear velocity vector, v₂ is the angular velocity vector, f₁ is the force vector acting on the vehicle, and  f₂ is the moment vector acting on the vehicle.

Fig. 2 Inertial and body-fixed coordinate systems

The new AUV in this work adopts NPS II AUV’s figure, accurate hydrodynamic coefficients of which have been obtained from the experiment [9]. The influence of the gravity, buoyancy, vectored thrust, rudder control forces, ocean current forces and wave disturbances are considered so as to establish a more integrated six-DOF dynamic model. The six-DOF kinematic and dynamic equations can be expressed as

                   (1)

         (2)

where J₁(h₂) is the transformation matrix that transforms the coordinate (x, y, z) in the body-fixed coordinate system into that in the inertial coordinate system, and J₂(h₂) is the transformation matrix that transforms the coordinate (p, q, r) in the body-fixed coordinate system into that in the inertial coordinate system. M=M_R+M_A, C(v)=C_R(v)+C_A(v), M_R is the new AUV’s generalized mass matrix, M_A is the added mass matrix, C_R(v) is the new AUV’s Coriolis and centripetal matrix, and C_A(v) is the hydrodynamic Coriolis and centripetal matrix. D(v) is the hydrodynamic damping matrix, and g(h) is the restoring force and moment vector in the body-fixed coordinate system. f_T is the control force and moment,   f_T = f_p+f_r, f_p is the total thrust and total torque of four vectored thrusters, and f_r is the force and moment of rudders; f_C is the ocean currents force and moment; f_W is the waves force and moment. The specific form of each item is found in Ref. [10].

According to the submarine theory, six-DOF motion equations of the AUV with large slender aspect ratio can be decomposed into two mutually non-coupled subsystems, namely the horizontal plane subsystem and the vertical plane subsystem [11-13]. Therefore, the non-linear tracking control problem of the new AUV can be studied on the horizontal plane and vertical plane, respectively.

In the motion equation of the horizontal plane, the main parameters are u, v, r, y, x and h, while other motion parameters can be ignored such as w, p, q, q, f and z. So, the horizontal kinematic equation of the new AUV derived from Eq. (1) can be expressed as

                  (3)

The generalized mass matrix of the new AUV in the horizontal kinetic equation can be written as

                  (4)

The new AUV’s Coriolis and centripetal matrix can be written as

   (5)

The added mass matrix can be written as

                       (6)

The hydrodynamic damping matrix of the new AUV can be written as

          (7)

Therefore, the dynamic equation of the new AUV with G=B, x_G=x_B and y_G=y_B on the horizontal plane is

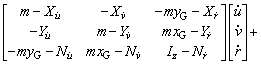
           (8)

where f_X, f_Y and f_N are axial force, lateral force and vertical torque of the new AUV in complex sea conditions, respectively.

Similarly, the kinematic and dynamic equations of the new AUV in vertical plane derived from Eq. (1) and Eq. (2) can be obtained:

                  (9)

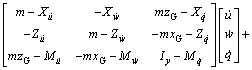
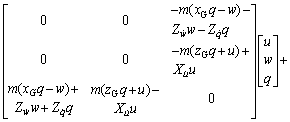
                   (10)

where f_Z and f_M are vertical force and lateral torque of the new AUV in complex sea conditions, respectively.

3 Nonlinear trajectory tracking control algorithm of new AUV

Because the efficiency of rudders is higher than vectored thrusters when the new AUV cruises at a relatively high speed in nonlinear trajectory tracking control, the nonlinear trajectory tracking control relies mainly on the rudders.

3.1 Trajectory tracking control algorithm on horizontal plane

The trajectory tracking control of the new AUV on horizontal plane means that the new AUV cruises in accordance with a predetermined route within a limited region of the horizontal plane. The predetermined route is usually composed of a number of connections between different path points. As the displacement of the new AUV on the horizontal plane cannot be measured directly, which could be got through the dead reckoning, the control algorithm can only be designed based on measurable yaw angle and yaw angle rate.

In order to make the new AUV accurately track the trajectory of the predetermined route on the horizontal plane, the sliding mode control algorithm combining cross track error method and line of sight method is used in this work. The cross track error method adjusts the new AUV’s position constantly according to its position error so as to achieve the desired target position. The cross track error and related parameters are defined in Fig. 3. The cross track error e(t) is the vertical distance from the center of the AUV to the adjacent routes, and the control strategy of the cross track error method is to keep e(t) at minimum.

Define the length of each route and the yaw angle respectively as

   (11)

=atan2  (12)

where (X_wpt(i), Y_wpt(i)) and (X_wpt(i-1), Y_wpt(i-1)) are the current and previous path points, respectively.

Fig. 3 Cross track error of new AUV

Therefore, the heading error of the i-th route segment can be obtained as

               (13)

where β(t) is the new AUV’s sideslip angle, and the heading error should be normalized between -180° and 180°.

The coordinate difference between the current position point and the i-th path point can be expressed as

                   (14)

So, the projection length of the distance from the center of the AUV to the i-th path point on the predetermined route can be expressed as

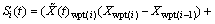
            (15)

In order to make the new AUV accurately track the predetermined route, the control system on the horizontal plane should be able to ensure De→0. According to the current position point, current path point and previous path point, the cross track error can be expressed as

                      (16)

where d_h(t) is the angle formed by the connection between the new AUV and the current path point and the predetermined route, which should be normalized between -180° and 180°:

=atan2

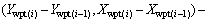
atan2                (17)

According to the definition of the cross track error, its first three-order derivatives can be expressed as

                      (18)

            (19)

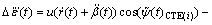
              (20)

Usually, the change rate of the sideslip angle is small compared with the angular velocity of the yaw angle, soandcan be ignored. The sliding surface of sliding mode controller based on cross track error can be designed as a second-order polynomial form:

              (21)

The condition of reducing cross track error based on the control mode of reaching law can be expressed as

(22)

In order to get the controller input, ignoring sideslip dynamic characteristic and high-order damping item, the new AUV’s heading dynamic characteristic can be expressed as

                         (23)

From Eqs. (18), (19) and (12) together with Eqs. (21) and (22), the sliding surface σ₁(t) and its derivative  can be expressed respectively as

(24)

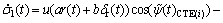
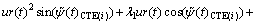
                      (25)

Then, from Eqs. (22) and (25), the control input of the vertical rudder can be expressed as

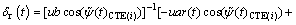
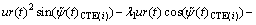
       (26)

In order to avoid the singular situation when , which leads to the new AUV’s heading vertical with the predetermined route, the commands of the rudder angle can be set to zero, because the occurrence of this case is transient in nature.

The case that the heading error is more than 40° often occurs in the navigation process of the new AUV. Especially, when the new AUV converts the route, the sudden heading change of 90° is not a infrequent case. In this case, the sliding mode controller based on the cross track error method fails and the sliding mode controller based on the line of sight method needs to be used for route guidance. The line of sight method assumes that a reference point on the predetermined route keeps a certain distance in front of the new AUV. Then, through constantly adjusting course deviation, the new AUV can track the predetermined route. The heading command of the line of sight method can be expressed as

=atan2    (27)

Then, the line of sight error can be written as

                     (28)

The slide surface is selected as

           (29)

The control law of the sliding mode controller based on the line of sight method is designed as

              (30)

where η₂tanh(σ₂(t)/f₂) is the reaching law of the sliding surface, η₂ is the maximum of the reaching law, and f₂ determines the decay law of the sliding surface when its amplitude decreases. The effect of this item mainly suppresses the impact of interference and unmodeled part, which can make the decay law of the line of sight error proportional to the amplitude of σ₂(t).

In the process of route tracking, how to convert route point is a very important issue. Two methods about route point conversion are explained in this work, which are used to activate the next path point. The first method is to determine whether the new AUV has reached the observed radius R_w(i) of a path point, which is equivalent to determine whether the new AUV tracks the predetermined route with small cross track error. The second method is to determine whether the projection distance S_i(t) is less than the limited amount ρ of the cross track error when the new AUV is guided by the cross track error method. The condition of route point conversion can be expressed as

 (31)

3.2 Depth tracking control algorithm in vertical plane

The function of depth tracking sliding mode controller is to make the new AUV reach the depth command with the desired attitude and stability through controlling the multi-state variables with the hydroplane angle when the depth command is received. Compared with the controller based on output errors, this controller can ensure the new AUV’s desired attitude and stability by adjusting the depth.

The dynamic equation of the new AUV’s hydroplane can be written as

                             (32)

The sliding surface based on the state variable errors of the new AUV in motion can be expressed as

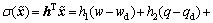
                   (33)

The dynamic equation with parameters of the new AUV can be expressed as

                               (34)

The sliding mode control law composed of linear and nonlinear parts can be expressed as

                                  (35)

where the linear part is chosen as , and k is the feedback gain vector.

From Eqs. (34) and (35), the closed-loop dynamic equation can be expressed as

                         (36)

where k can be computed by means of pole-placement.

Pre-multiplying Eq. (36) with h^T and then subtracting  from both sides, the derivative of the sliding surface can be expressed as

           (37)

The nonlinear part of the sliding mode control law can be chosen as

               (38)

Hence,

             (39)

In order to keep the continuity of the control input, sgn(σ) is changed into the saturation function sgn(σ). Hence, the sliding mode control law can be expressed as

         (40)

From if one of the eigenvalues of is specified to be zero, the corresponding eigenvector h can be obtained by

                            (41)

With this choice of h, the derivative of the sliding surface can be expressed as

                        (42)

In order to verify the asymptotic stability of the system, the Lyapunov function is designed as

                                  (43)

Hence, the derivative of the Lyapunov function can be obtained:

                 (44)

Choose η>0, which ensures that . Hence, the control system is asymptotically stable.

As the dynamic characteristic of the hydroplane is considered, the amplitude and rate constraints of the hydroplane angle easily lead to the control failure based on the static boundary layer. In order to avoid the reduction of tracking performance caused by increasing the thickness of the boundary layer, the dynamic boundary layer method is used to improve the stability of the system. The boundary layer thickness e  needs to meet the following three conditions:

1) In order to keep the saturation function in linear region so as to avoid the sliding mode controller saturating, the inequation can be expressed as

                                    (45)

Hence, .

2) In order to meet the amplitude constraint of the hydroplane angle, the inequation can be expressed as

       (46)

Hence,

,

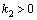
3) In order to meet the rate constraint of the hydroplane angle, the inequation can be expressed as

                     (47)

Hence, , .

The choice of dynamic boundary layer will be a trade-off between avoiding the saturation of the sliding mode controller and reducing the domain of attraction range, which can be expressed as

                          (48)

4 Trajectory tracking control results of new AUV in complex sea conditions

4.1 Trajectory tracking control results of new AUV in horizontal plane

In order to verify the performance of the trajectory tracking controller on the horizontal plane, the S-shaped predetermined route usually selected by field test platforms is used. The predetermined route is designed as (0, 0)→(275, 60)→(275, 120)→(25, 120)→(25, 180)→ (275, 180)→(275, 240)→(25, 240). The amplitude of the vertical rudder angle is limited in [-π/3, π/3]. The four vectored thrusters point to the tail of the new AUV and the rotational speed of the propellers is n=5 r/s. The sliding mode controller combining cross track error method and line of sight method is used to guide the horizontal trajectory of the new AUV. The trajectory tracking capability of the new AUV on the horizontal plane is discussed in different sea conditions.

The trajectory tracking result on the horizontal plane when the new AUV navigates in the absence of currents and wave is shown in Fig. 4. The new AUV can track the predetermined route accurately and the cross track error is slightly larger only at the turning, as shown in Fig. 5. Figure 6 shows the change of vertical rudder angle and the yaw angle of the new AUV, which denotes that the vertical rudder responds quickly at the turning under the effect of the sliding mode controller so as to ensure that the yaw angle of the new AUV makes moderate changes.

Fig. 4 Trajectory tracking result in non-interference environment

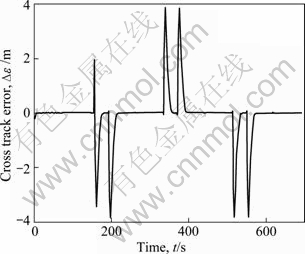
Fig. 5 Cross track error in non-interference environment

In the non-ideal conditions, the trajectory tracking control of the new AUV is not possibly implemented in non-interference environment, whose movement will be subjected to wind, waves, currents and other external interference. According to wave theory, the interference caused by waves rather than currents can be ignored when the new AUV submerges to a certain depth.

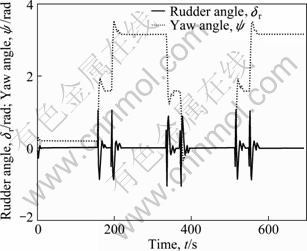
Fig. 6 Rudder angle d_r and yaw angle y in non-interference environment

When the new AUV navigates in deep water, the angle of attack α_c=15° and the angle of sideslip of flow axis β_c=25°. The computational results of the   trajectory tracking are shown in Figs. 7, 8 and 9. It can be seen from these figures that, the AUV can track the predetermined route perfectly on the impact of the currents. Compared with the performance of the trajectory tracking in non-interference environment, the cross track error increases a little and the vertical rudder angle and the yaw angle of the new AUV vibrate more severely.

Fig. 7 Trajectory tracking result in random currents

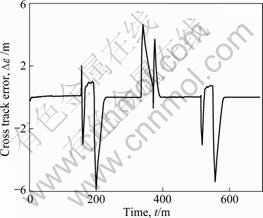
Fig. 8 Cross track error in random currents

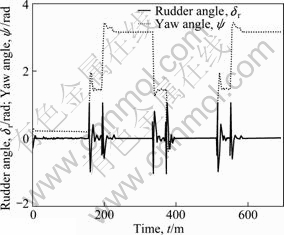
Fig. 9 Rudder angle d_r and yaw angle y in random currents

With the development of AUVs, the large range has become one of the objectives pursued by military and civilian AUVs urgently. When the range increases, the AUV needs to ascend near the surface to receive positioning signals such as GPS, which ensures the correct course of the AUV. At this time, the waves disturbance on the trajectory tracking control of the AUV must be considered [14-15].

Defining the ocean wave grade S=5, significant wave height H_s=3.2 m, and the encounter angle c=0°, the computational results of the trajectory tracking by the interference of random waves are shown in Figs. 10, 11 and 12. These figures show that the values of the cross track error resemble those in non-interference conditions. The computational route fluctuates around the predetermined route. The vertical rudder angle and the yaw angle of new AUV appear nonperiodic oscillation in random wave interference. The computational results show that the controller has good control performance in the random waves interference, which can meet the control requirements of the new AUV sailing in random waves.

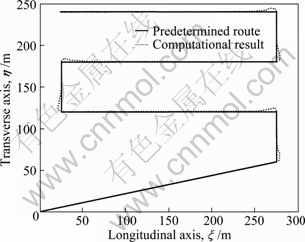
Fig. 10 Trajectory tracking result in random waves

Fig. 11 Cross track error in random waves

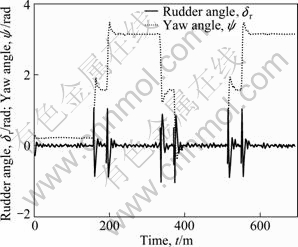
Fig. 12 Rudder angle d_r and yaw angle y in random waves

4.2 Depth tracking control results of new AUV on vertical plane

In order to verify the performance of the depth tracking controller on the vertical plane, the Z-shaped predetermined depth usually selected by field test platforms is used. Predetermined depth is designed as  (0, 80)→(250, 80)→(250, 40)→(500, 40)→(500, 80)→ (750, 80)→(750, 40)→(1 000, 40). The amplitude of the hydroplane angle is limited in [-π/3, π/3] and the rate of the hydroplane angle is limited in [-20, 20]. The four vectored thrusters point to the tail of the new AUV and the speed of the new AUV is 5 m/s. The sliding mode controller based on single-input multi-state system is used to compute the depth tracking capability in two different cases.

The depth tracking result on the vertical plane when the new AUV navigates in the absence of currents and wave is shown in Fig. 13. The sliding mode controller has good tracking performance for the time-varying depth signal. The new AUV adjusts the pitch angle with the hydroplane angle to track the predetermined depth and the amplitude limit of the hydroplane angle is reached when the predetermined depth changes, as shown in Fig. 14. Figure 15 shows the changes of the dynamic boundary layer and sliding surface of sliding mode controller. The depth tracking performance and stability of the sliding mode controller are ensured through adjusting the thickness of the dynamic boundary layer.

Fig. 13 Depth tracking result in non-interference environment

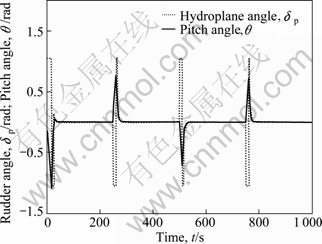
Fig. 14 Hydroplane angle d_p and pitch angle q in non-interference environment

Fig. 15 Sliding surface s and boundary layer e in non-interference environment

In the non-ideal conditions, the depth tracking control of the new AUV will be subjected to the action of waves and currents. Due to the fact that currents are usually considered to have no weight in the vertical direction, the impact of currents on the depth tracking control is regardless. The depth tracking performance of the new AUV in random waves is computed in this work.

Defining the ocean wave grade S=5, significant wave height H_s=3.2 m, and the encounter angle c=0°, the computational results of the depth tracking by the interference of random waves are shown in Fig. 16. It can be seen that the new AUV can track the predetermined depth accurately. Compared to the results without environmental interference, the computational depth appears nonperiodic oscillation around the predetermined route. Due to the interference of random waves, the hydroplane angle and the pitch angle of the new AUV also appear nonperiodic oscillation and the amplitude limit of the hydroplane angle is reached, as shown in Fig. 17. Figure 18 shows the changes of the dynamic boundary layer and sliding surface of the sliding mode controller. The depth tracking performance and stability of the sliding mode controller by the random waves interference are ensured through adjusting the thickness of the dynamic boundary layer continuously.

Fig. 16 Depth tracking result in random waves

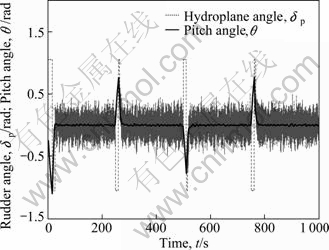
Fig. 17 Hydroplane angle d_p and pitch angle q in random waves

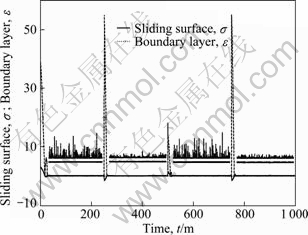
Fig. 18 Sliding surface s and boundary layer e in random waves

5 Conclusions

1) The six-DOF kinematic and dynamic models of the new AUV are established considering the influence of the gravity, buoyancy, vectored thrust, rudder control forces, ocean current forces and wave disturbances. According to the theory of submarines, the six-DOF kinematic and dynamic models are decomposed into two mutually non-coupled vertical and horizontal plane subsystems, which can solve the design problem of the control systems where the measurable values are different on the different planes.

2) Because the yaw angle and yaw angle rate rather than the displacement of the new AUV on the horizontal plane can be measured directly, the sliding mode control algorithm combining cross track error method and line of sight method is used to fulfill high-precision trajectory tracking control in complex sea conditions, which also ensures the robustness and control accuracy of sliding mode controller when the heading error is too large.

3) As the vertical displacement of the new AUV can be measured, a stable sliding mode controller is designed based on the single-input multi-state system, which takes into account the characteristic of the hydroplane and the amplitude and rate constraints of the hydroplane angle. Moreover, the application of dynamic boundary layer improves the robustness and control accuracy of the system, which realizes the accurate tracking of time-varying depth signal with the desired attitude in complex sea conditions.

4) The good performance of the sliding mode controller designed in this work is verified by comparing the trajectory tracking results of the new AUV in different sea conditions. The impacts of currents and waves on the new AUV’s sliding mode controller are analyzed qualitatively and quantitatively, which provides an effective reference to the design of the AUV’s control system in real complex sea conditions.

References

[1] PAN Cun-yun, WEN Xi-sen. Research on transmission principle and kinematic analysis for involute spherical gear [J]. Journal of Mechanical Engineering, 2005, 41(5): 1-9. (in Chinese)

[2] GAO Fu-dong, PAN Cun-yun, YANG Zheng, FENG Qing-tao. Nonlinear mathematics modeling and analysis of the vectored thruster autonomous underwater vehicle in 6-DOF motions [J]. Journal of Mechanical Engineering, 2011, 47(5): 93-100. (in Chinese)

[3] BESSA W M, DUTRA M S, KREUZER E. Depth control of remotely operated underwater vehicles using an adaptive fuzzy sliding mode controller [J]. Robotics and Autonomous Systems, 2008, 56(8): 670-677.

[4] BESSA W M, DUTRA M S, KREUZER E. An adaptive fuzzy sliding mode controller for remotely operated underwater vehicles [J]. Robotics and Autonomous Systems, 2010, 58(1): 16-26.

[5] CAO Yong-hui, SHI Xiu-hua. Trajectory tracking control and simulation of AUV [J]. Computer Simulation, 2006, 23(7): 19-21. (in Chinese)

[6] CHEN Tong, XU Shi-jie. Approach guidance with double-line-of- sight measuring navigation constraint for autonomous rendezvous [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 678-687.

[7] RADHAKRISHNAN K, UNNIKRISHNAN A, BALAKRISHNAN K G. Bearing only tracking of maneuvering targets using a single coordinated turn model [J]. International Journal of Computer Applications, 2010, 1(1): 25-33.

[8] BERGLUND T, BRODNIK A, JONSSON H, STAFFANSON M, SODERKVIST I. Planning smooth and obstacle-avoiding B-spline paths for autonomous mining vehicles [J]. Automation Science and Engineering, 2010, 7(1): 167-172.

[9] DONALD P B. A virtual world for an autonomous underwater vehicle [D]. Washington: Naval Postgraduate School, 1992.

[10] GAO Fu-dong, PAN Cun-yun, XU Xiao-jun, ZHANG Xiang. Nonlinear dynamic characteristics of the vectored thruster AUV in complex sea conditions [J]. Chinese Journal of Mechanical Engineering, 2011, 24(6): 935-946.

[11] YOU S S, CHOI H S, KIM H S, PARK H I. Autopilot control synthesis for path tracking maneuvers of underwater vehicles [J]. China Ocean Engineering, 2011, 25(2): 237-249.

[12] LAPIERRE L, JOUVENCEL B. Robust nonlinear path-following control of an AUV [J]. IEEE Journal of Oceanic Engineering, 2008, 33(2): 89-102.

[13] PEDRO B, CARLOS S, PAULO O. A time differences of arrival-based homing strategy for autonomous underwater vehicles [J]. International Journal of Robust and Nonlinear Control, 2010, 20(15): 1758-1773.

[14] JUNG Y S, LEE K W, LEE S Y, CHOI M H, LEE B H. An efficient underwater coverage method for multi-AUV with sea current disturbances [J]. International Journal of Control, Automation and Systems, 2009, 7(4): 615-629.

[15] KIM K, URA T. Optimal Guidance for Autonomous underwater vehicle navigation within undersea areas of current disturbances [J]. Advanced Robotics, 2009, 23(5): 601-628.

(Edited by YANG Bing)

Foundation item: Project(2006AA09Z235) supported by the National High Technology Research and Development Program of China; Project(CX2009B003) supported by Hunan Provincial Innovation Foundation For Postgraduates, China

Received date: 2011-10-12; Accepted date: 2012-02-20

Corresponding author: GAO Fu-dong, PhD; Tel: +86-731-84574932; E-mail: gaofudong2005@163.com