文章编号:1004-0609(2015)-09-2335-07
AZ41M镁合金动态再结晶临界条件
蔡志伟1, 2,陈拂晓1, 2,郭俊卿1, 2
(1. 河南科技大学 材料科学与工程学院,洛阳 471023;
2. 河南科技大学 有色金属共性技术河南省协同创新中心,洛阳 471023)
摘 要:采用Gleeble-1500D型热/力模拟试验机在变形温度300~450 ℃、应变速率0.005~1 s-1条件下对AZ41M镁合金进行热模拟压缩试验。用计算加工硬化率的方法处理试验数据,再结合lnθ-ε曲线的拐点及– (lnθ)/
(lnθ)/ ε-ε曲线最小值判据,建立合金热变形过程中的动态再结晶临界应变模型。根据热压缩实验数据,分析温度和应变速率等工艺参数对合金动态再结晶的影响。结果表明:在该实验条件下,AZ41M镁合金的lnθ-ε曲线均具有拐点特征,对应的-
ε-ε曲线最小值判据,建立合金热变形过程中的动态再结晶临界应变模型。根据热压缩实验数据,分析温度和应变速率等工艺参数对合金动态再结晶的影响。结果表明:在该实验条件下,AZ41M镁合金的lnθ-ε曲线均具有拐点特征,对应的- (lnθ)/
(lnθ)/ ε-ε曲线均出现最小值,该最小值所对应的应变即为临界应变εc,得到合金临界应变预测模型;临界应变随变形温度的降低和应变速率的增加而增大,且峰值应变εp和临界应变εc的比值满足εp/εc = 1.97。
ε-ε曲线均出现最小值,该最小值所对应的应变即为临界应变εc,得到合金临界应变预测模型;临界应变随变形温度的降低和应变速率的增加而增大,且峰值应变εp和临界应变εc的比值满足εp/εc = 1.97。
关键词: AZ41M镁合金;加工硬化率;动态再结晶;临界条件;组织演变
中图分类号:TG111.7 文献标志码:A
Critical conditions of dynamic recrystallization for AZ41M magnesium alloy
CAI Zhi-wei1, 2, CHEN Fu-xiao1, 2, GUO Jun-qing1, 2
(1. School of Materials Science and Engineering,
Henan University of Science and Technology, Luoyang 471023, China;
2. Collaborative Innovation Center of Nonferrous Metals of Henan Province,
Henan University of Science and Technology, Luoyang 471023, China)
Abstract: The hot simulation compression tests of AZ41M magnesium alloy were conducted at deformation temperature in the range of 300-450 ℃ and strain rate in the range of 0.005-1 s-1 with the Gleeble-1500D thermal-mechanical simulation test machine. The critical strain model of dynamic recrystallization for AZ41M magnesium alloy during hot deformation was obtained by computing the work hardening rate θ from initial experimental data and combining with the inflection point criterion of lnθ-ε curves and the minimum value criterion of - (lnθ)/
(lnθ)/ ε-ε curves. The influences of temperature and strain rate on the dynamic recrystallization were investigated based on the experimental data. The results show that an inflection point presents in the lnθ-ε curve and a minimum value appears in the corresponding –
ε-ε curves. The influences of temperature and strain rate on the dynamic recrystallization were investigated based on the experimental data. The results show that an inflection point presents in the lnθ-ε curve and a minimum value appears in the corresponding – (lnθ)/
(lnθ)/ ε-ε curve when the critical state of AZ41M magnesium alloy is attained, the strain that relates to the minimum value is the critical strain εc. The predicting model of critical strain is described. The critical strain increases with the decrease of deformation temperature and the increase of strain rate, and the ratio of peak strain (εp) and critical strain εc is 1.97.
ε-ε curve when the critical state of AZ41M magnesium alloy is attained, the strain that relates to the minimum value is the critical strain εc. The predicting model of critical strain is described. The critical strain increases with the decrease of deformation temperature and the increase of strain rate, and the ratio of peak strain (εp) and critical strain εc is 1.97.
Key words: AZ41M magnesium alloy; work hardening rate; dynamic recrystallization; critical condition; microstructure evolution
镁合金是现代工业生产中最轻的金属结构材料,在电子通讯、汽车制造及航空航天等领域应用前景广阔[1]。但镁合金的密排六方晶体结构使其室温变形能力较差[2],热塑性加工成为其成形的主要方式。
在镁合金的热塑性变形过程中,动态再结晶是一种重要的组织演化机制。动态再结晶不仅可以细化晶粒,还能消除缺陷,提高力学性能[3],对改善镁合金塑性成形能力起到积极的促进作用。动态再结晶刚开始发生时的应变即为临界应变,只有当实际变形程度超过临界应变时,动态再结晶才能发生[4]。童小山等[5]建立了ZM21及ZM61镁合金动态再结晶临界应变模型,发现两者的临界应变均随应变速率的增加而升高,随变形温度的增加而降低。黄光杰等[6]采用单参数方法,建立起AZ31镁合金临界应变与变形条件的定量关系。研究人员对AZ41M镁合金的动态再结晶行为进行了研究,WANG等[7]研究了双辊铸轧AZ41M镁合金板料的变形行为及动态再结晶机制,王忠军等[8]研究了铸造AZ41镁合金动态再结晶与位错运动的协调关系,但挤压态AZ41M镁合金动态再结晶临界条件及相关模型的研究却鲜有报道。
AZ41M属于Mg-Al-Zn-Mn系合金,是制造飞机内部构件、舱门、壁板及导弹蒙皮等的优良材料[9]。此外,该类镁合金一般通过模锻成形,为了提高可加工性,需要先通过挤压使坯料预成形[10],因此,研究挤压态AZ41M镁合金的动态再结晶行为具有重要应用价值。本文作者以模拟挤压态AZ41M镁合金热压缩所获得的实验数据为基础,通过对加工硬化率曲线的特征点进行识别,构建了涵盖应变速率及变形温度的动态再结晶临界应变模型,以期为热加工工艺的制定、组织性能的控制提供理论支持。
1 实验
实验材料为挤压态AZ41M镁合金,其化学成分如表1所列。原始铸锭在400 ℃条件下均匀化处理12 h,然后以13 mm/s的速度挤压,挤压温度为350 ℃,挤压比为7.32。再用线切割加工出轴向平行于压缩方向的d10 mm×15 mm圆柱试样,压缩前在试样两端面均匀涂敷润滑剂,以减小摩擦对实验结果的影响。使用Gleeble-1500D型热/力模拟机沿轴向对试样进行压缩,变形温度t为300、350、400和450 ℃,应变速率 为0.005、0.05、0.1和1 s-1。实验时将试样以5 ℃/s的升温速率加热到预定温度,保温3 min以消除试样内部温度梯度,然后压缩至真应变0.7。试样经压缩后立即水淬,以保留热变形组织。将变形后试样沿平行于压缩方向的轴截面切开,然后经过镶嵌、预磨、抛光和腐蚀处理后,采用Olympus-PMG3型金相显微镜观察显微组织。金相侵蚀采用5 g苦味酸+5 mL冰醋酸+100 mL无水乙醇+10 mL蒸馏水的腐蚀剂。
为0.005、0.05、0.1和1 s-1。实验时将试样以5 ℃/s的升温速率加热到预定温度,保温3 min以消除试样内部温度梯度,然后压缩至真应变0.7。试样经压缩后立即水淬,以保留热变形组织。将变形后试样沿平行于压缩方向的轴截面切开,然后经过镶嵌、预磨、抛光和腐蚀处理后,采用Olympus-PMG3型金相显微镜观察显微组织。金相侵蚀采用5 g苦味酸+5 mL冰醋酸+100 mL无水乙醇+10 mL蒸馏水的腐蚀剂。
表1 AZ41M镁合金的化学成分
Table 1 Chemical composition of AZ41M magnesium alloy (mass fraction, %)

2 结果与分析
2.1 流变曲线
图1所示为AZ41M镁合金在不同实验条件下的真应力-真应变曲线。由图1可知,变形初期流变应力随应变的增加而迅速上升,这是由于变形过程中位错大量增殖并发生堆积和缠结[11],位错密度增加,阻碍了位错的运动,产生加工硬化现象[12-13];当应变量增加到一定程度时,变形储能增加,发生动态再结晶软化[14],抵消了部分加工硬化,但此阶段加工硬化仍然占主导地位,因此流变曲线仍呈上升趋势,但斜率下降;随着应变量继续增加,软化速率不断加快,当动态软化与加工硬化达到平衡时,曲线出现峰值,而当软化作用开始占主导地位时,曲线则平缓下降。总体而言,图1所示的流变曲线呈现出单峰现象,具有典型的动态再结晶特征[15]。此外,合金的峰值应力和稳态应力都随着变形温度的升高或应变速率的降低而减小,说明AZ41M镁合金属于热敏感型和应变速率敏感型材料。
2.2 动态再结晶临界应变
2.2.1 基于加工硬化率的临界应变分析
发生动态再结晶的临界应变是研究动态再结晶的重要指标,而流变应力曲线无法直观地反映出临界应变值,需要对流变应力曲线进行加工硬化率处理。POLIAK等[16]研究表明,发生动态再结晶时,材料的θ-σ曲线(θ= σ/
σ/ ε,其中,σ为真应力,ε为真应变)呈现拐点特征,即-
ε,其中,σ为真应力,ε为真应变)呈现拐点特征,即- 2θ/
2θ/ σ=0,而此拐点与-
σ=0,而此拐点与- θ/
θ/ σ-σ曲线的最小值点对应。可利用偏导数推导出如下关系:–
σ-σ曲线的最小值点对应。可利用偏导数推导出如下关系:– (lnθ)/
(lnθ)/ ε=
ε= θ/
θ/ σ,说明不仅θ-σ曲线呈现拐点特征,lnθ-ε曲线也必然具有相应的拐点特征[17]。则根据AZ41M镁合金热压缩试验数据绘制lnθ-ε和–
σ,说明不仅θ-σ曲线呈现拐点特征,lnθ-ε曲线也必然具有相应的拐点特征[17]。则根据AZ41M镁合金热压缩试验数据绘制lnθ-ε和– (lnθ)/
(lnθ)/ ε-ε曲线,再利用–
ε-ε曲线,再利用– 2(lnθ)/
2(lnθ)/ ε=0判据即可得到相应的临界应变值εc。
ε=0判据即可得到相应的临界应变值εc。

图1 不同条件下AZ41M镁合金的真应力-真应变曲线
Fig. 1 True stress-strain curves of AZ41M magnesium alloy under different conditions
实验得到的真应力-真应变曲线不光滑而呈现波浪型,为了便于通过实验数据获得加工硬化率θ,需要先对真应力-真应变曲线进行拟合,获得相关性较好的拟合方程,再通过微分运算求得各真应变下的拟合曲线斜率,最后绘制lnθ-ε曲线,确定临界应变。
研究人员对TA15钛合金[17]、TC11钛合金[18]的真应力-真应变曲线进行拟合,均取得较好效果。本文作者采用不同方式对各变形条件下的真应力-真应变曲线进行拟合,以温度350 ℃、应变速率0.05 s-1条件下的拟合为例,所用方程及所得相关性系数R如式(1)~(5)所示:

对比发现,对于温度350 ℃、应变速率0.05 s-1条件下的真应力-真应变拟合曲线,式(1)相关性系数最大,能更好地反映曲线规律,且对于式(3)~(5),当指数大于10就会出现拟合不收敛情况,因此该条件下选取式(1)为拟合方程,拟合所得结果如图2所示。

图2 变形温度350 ℃、应变速率0.05 s-1时的真应力-真应变实测曲线与拟合曲线
Fig. 2 Experimental curve and fitting curve deformed at temperature of 350 ℃ and strain rate of 0.05 s-1
由图2可得真应力-真应变曲线拟合方程如式(6)所示:
σ=(0.00628 + 2.4904ε + 925.45393ε2 +
123.50877ε3 + 11643.17837ε4 - 18403.36542ε5)/
(0.0006765 + 0.0282ε + 12.92082ε2 - 33.7816ε3+
440.35182ε4-702.58379ε5+182.06091ε6) (6)
根据式(6)可求得各真应变下的加工硬化率θ,进而绘制出lnθ-ε曲线,并采用三次方程进行拟合,所得结果如图3(a)所示。由图3(a)可知,lnθ-ε曲线在真应变0.03附近出现拐点,为了精确地确定拐点的具体位置,得出lnθ-ε曲线拟合方程:
lnθ=9.27971-240.25667ε+5971.91411 ε2-57296.8217 ε3(7)
对式(7)进行微分,利用运算结果绘制出– (lnθ)/
(lnθ)/ ε-ε曲线,如图3(b)所示,曲线方程为
ε-ε曲线,如图3(b)所示,曲线方程为
– (lnθ)/
(lnθ)/ ε=240.25667–11943.82822 ε+171890.4651 ε2(8)
ε=240.25667–11943.82822 ε+171890.4651 ε2(8)
在图3(b)中,当– 2(lnθ)/
2(lnθ)/ ε=0时所对应的应变即为临界应变,则温度350 ℃、应变速率0.05 s-1时所对应的临界应变εc为0.0347。
ε=0时所对应的应变即为临界应变,则温度350 ℃、应变速率0.05 s-1时所对应的临界应变εc为0.0347。

图3 在变形温度350 ℃、应变速率0.05 s-1时lnθ与应变ε及– (lnθ)/
(lnθ)/ ε与应变ε之间的关系
ε与应变ε之间的关系
Fig. 3 Relationships among lnθ and ε (a) and – (lnθ)/
(lnθ)/ ε and ε (b) at temperature of 350 ℃ and strain rate of 0.05 s-1
ε and ε (b) at temperature of 350 ℃ and strain rate of 0.05 s-1
2.2.2 临界应变模型的建立
采用以上相同的方法,可绘制其他热变形条件下的lnθ-ε曲线,所得结果如图4所示。由图4可知,不同温度(见图4(a))及不同应变速率(见图4(b))下lnθ-ε曲线的变化规律相似。变形初期,加工硬化率随应变的增加快速下降,然后进入缓慢降低阶段,到最后又快速下降,在加工硬化速率缓慢降低阶段的某处曲线出现拐点。

图4 不同变形条件下lnθ与ε之间的关系
Fig. 4 Relationships between lnθ and ε under different deformation conditions
图5所示为不同变形条件下对应于lnθ-ε曲线的– (lnθ)/
(lnθ)/ ε-ε关系曲线。由图5可知,–
ε-ε关系曲线。由图5可知,– (lnθ)/
(lnθ)/ ε-ε曲线均出现最小值,且曲线最小值与lnθ-ε曲线的拐点位置相对应,最小值处所对应的应变值即为动态再结晶临界应变。
ε-ε曲线均出现最小值,且曲线最小值与lnθ-ε曲线的拐点位置相对应,最小值处所对应的应变值即为动态再结晶临界应变。
图6所示为不同变形温度、应变速率对临界应变εc及峰值应变εp影响的三维线框架面图。由图6可知,变形温度对临界应变及峰值应变的影响为负,即在同一应变速率下,临界应变及峰值应变均随着变形温度的升高而降低。这是因为温度越高,原子热振荡及扩散速率越快,位错迁移的驱动力越强[17],滑移系临界切应力越低[19-20],则动态再结晶更容易发生。此外,应变速率对临界应变及峰值应变的影响为正,即在同一变形温度下,临界应变及峰值应变均随着应变速率的增加而增大。这是因为应变速率越大,位错合并抵消的时间越少,再结晶晶粒也越来不及形核和长大[14],则动态再结晶较难发生。
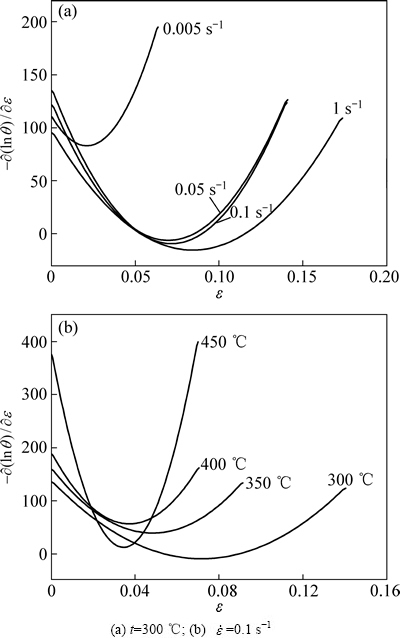
图5 不同变形条件下– (lnθ)/
(lnθ)/ ε与ε之间的关系
ε与ε之间的关系
Fig. 5 Relationships between – (lnθ)/
(lnθ)/ ε and ε under different deformation conditions
ε and ε under different deformation conditions

图6 不同变形温度和应变速率对峰值应变及临界应变的影响
Fig. 6 Effect of different deformation temperatures and strain rates on peak strain and critical strain
为了定量分析变形温度及应变速率对动态再结晶临界应变的影响,本文作者引入涵盖变形温度和应变速率的Sellars[21]模型结构来表征临界应变模型:
 (9)
(9)
式中:a、b均为常数;Z为温度补偿应变速率因子,  ,其中Q为变形激活能,对实验数据进行多次线性回归处理,并根据
,其中Q为变形激活能,对实验数据进行多次线性回归处理,并根据 计算得到本实验条件下的变形激活能Q为165.2049 kJ/mol。
计算得到本实验条件下的变形激活能Q为165.2049 kJ/mol。
对式(9)两边取对数,可得:
 (10)
(10)
求出不同变形温度和应变速率下的临界应变εc和参数Z,绘制lnεc-lnZ散点图,并进行单因素线性回归,所得结果如图7所示。由式(10)可知,图7直线截距即为lna,斜率为b,进而求得a=2.58×10-4,b=0.17356,则所求临界应变预测模型为
 (11)
(11)
临界应变εc与峰值应变εp基本上也呈现线性关系,进一步对其进行单因素线性回归,所得结果如图8所示,可得临界应变与峰值应变之间的关系:
εp=1.97εc (12)
由式(12)可知,峰值应变比临界应变滞后,即动态再结晶在应变量达到峰值应变之前就已经发生。
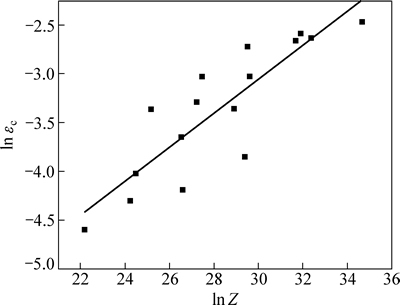
图7 lnεc与lnZ之间的关系
Fig. 7 Relationship between lnεc and lnZ

图8 临界应变与峰值应变的关系
Fig. 8 Relationship between critical strain and peak strain
2.2.3 显微组织演变
图9所示为AZ41M镁合金挤压态及不同条件下变形后的光学显微组织。由图9(a)可知,AZ41M镁合金原始挤压态组织由等轴晶组成,平均晶粒尺寸约为29.37 μm。当t=400 ℃、 =1 s-1、应变量ε为0.07时(见图9(b),该条件下的临界应变εc约为0.066 ),晶界呈锯齿状,初始动态再结晶晶粒开始在原始晶粒交界处形核。当应变量增加至0.2时(见图9(c)),再结晶晶粒增多,并呈项链状分布于原始粗大晶粒周围。当应变量继续增加到0.7时(见图9(d)),已发生完全动态再结晶,此时组织较为均匀,材料力学性能良好,平均晶粒尺寸约为7.34 μm。
=1 s-1、应变量ε为0.07时(见图9(b),该条件下的临界应变εc约为0.066 ),晶界呈锯齿状,初始动态再结晶晶粒开始在原始晶粒交界处形核。当应变量增加至0.2时(见图9(c)),再结晶晶粒增多,并呈项链状分布于原始粗大晶粒周围。当应变量继续增加到0.7时(见图9(d)),已发生完全动态再结晶,此时组织较为均匀,材料力学性能良好,平均晶粒尺寸约为7.34 μm。

图9 AZ41M镁合金挤压态不同条件下变形后的光学显微组织
Fig. 9 Optical microstructures of AZ41M magnesium alloy deformed under different conditions
3 结论
1) AZ41M镁合金流变曲线表现出典型的动态再结晶特征,其显微组织演变证明热变形过程中动态再结晶的发生。
2) 处理实验数据所得的lnθ-ε曲线均具有拐点特征,对应的– (lnθ)/
(lnθ)/ ε-ε曲线均出现最小值。利用此拐点判据,可以确定AZ41M镁合金在温度300~450 ℃、应变速率0.005~1 s-1条件下发生动态再结晶的临界条件,且其临界应变预测模型函数关系可表示为εc=2.58×10-4Z0.17356。
ε-ε曲线均出现最小值。利用此拐点判据,可以确定AZ41M镁合金在温度300~450 ℃、应变速率0.005~1 s-1条件下发生动态再结晶的临界条件,且其临界应变预测模型函数关系可表示为εc=2.58×10-4Z0.17356。
3) 动态再结晶临界应变随变形温度的降低和应变速率的增加而增大,且峰值应变和临界应变的比值满足εp/εc=1.97。
REFERENCES
[1] YU Hui, YU Hua-shun, KIM Young-min, YOU Bong-sun, MIN Guang-hui. Hot deformation behavior and processing maps of Mg-Zn-Cu-Zr magnesium alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(3): 756-764.
[2] KARAMI M, MAHMUDI R. Hot shear deformation constitutive analysis and processing map of extruded Mg-12Li-1Zn BCC alloy[J]. Materials and Design, 2014, 53: 534-539.
[3] XU Yan, HU Lian-xi, SUN Yu. Dynamic recrystallization kinetics of as-cast AZ91D alloy[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(6): 1683-1689.
[4] 陈振华, 许芳艳, 傅定发, 夏伟军. 镁合金的动态再结晶[J]. 化工进展, 2006, 25(2): 140-146.
CHEN Zhen-hua, XU Fang-yan, FU Ding-fa, XIA Wei-jun. Dynamic recrystallization of magnesium alloy[J]. Chemical Industry and Engineering Progress, 2006, 25(2): 140-146.
[5] 童小山, 彭 建, 石大伟, 潘复生, 彭 毅. ZM21及ZM61合金的热变形行为与动态再结晶临界条件的表征[J]. 中国有色金属学报, 2013, 23(8): 2069-2076.
TONG Xiao-shan, PENG Jian, SHI Da-wei, PAN Fu-sheng, PENG Yi. Thermal compression behavior and characterization of dynamic recrystallization critical conditions for ZM21 and ZM61 magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(8): 2069-2076.
[6] 黄光杰, 钱宝华, 汪凌云, JONAS J J. AZ31镁合金初始动态再结晶的临界条件研究[J]. 稀有金属材料与工程, 2007, 36(12): 2080-2083.
HUANG Guang-jie, QIAN Bao-hua, WANG Ling-yun, JONAS J J. Study on the critical conditions for initial dynamic recrystallization of AZ31 magnesium alloy[J]. Rare Metal Materials and Engineering, 2007, 36(12): 2080-2083.
[7] WANG Shou-ren, SONG Ling-hui, KANG Suk-bong, CHO Jaeh-yung, WANG Ying-zi. Deformation behavior and microstructure evolution of wrought magnesium alloys[J]. Chinese Journal of Mechanical Engineering, 2013, 26(3): 437-447.
[8] 王忠军, 乐启炽, 郭世杰, 崔建忠, 张彩碚. 低频电磁铸造AZ41镁合金的热压缩流变与组织[J]. 中国有色金属学报, 2006, 16(1): 123-129.
WANG Zhong-jun, LE Qi-chi, GUO Shi-jie, CUI Jian-zhong, ZHANG Cai-bei. Thermal compressing flow and microstructure of AZ41 magnesium alloy cast by low frequency electrical magnetic field[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(1): 123-129.
[9] 陈振华. 变形镁合金[M]. 北京: 化学工业出版社, 2005: 21.
CHEN Zhen-hua. Wrought magnesiumalloy[M]. Beijing: Chemical Industry Press, 2005: 21.
[10] LI Hui-zhong, WEI Xiao-yan, OUYANG Jie, JIANG Jun, LI Yi. Hot deformation behavior of extruded AZ80 magnesium alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(11): 3180-3185.
[11] 申利权, 杨 旗, 靳 丽, 董 杰. AZ31B镁合金在高应变速率下的热压缩变形行为和微观组织演变[J]. 中国有色金属学报, 2014, 24(9): 2195-2204.
SHEN Li-quan, YANG Qi, JIN Li, DONG Jie. Deformation behavior and microstructure transformation of AZ31B Mg alloy under high strain rate compression[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(9): 2195-2204.
[12] LIAO Ching-hao, WU Horng-yu, LEE Shyong, ZHU Feng-jun, LIU Hsu-cheng, WU Cheng-tao. Strain-dependent constitutive analysis of extruded AZ61 Mg alloy under hot compression[J]. Materials Science and Engineering A, 2013, 565: 1-8.
[13] WU Horng-yu, WU Cheng-tao, YANG Jie-chen, LIN Ming-jie. Hot workability analysis of AZ61 Mg alloys with processing maps[J]. Materials Science and Engineering A, 2014, 607: 261-268.
[14] QUAN Guo-zheng, SHI Yu, WANG Yi-xin, KANG Beom-soo, KU Tae-wan, SONG Woo-jin. Constitutive modeling for the dynamic recrystallization evolution of AZ80 magnesium alloy based on stress-strain data[J]. Materials Science and Engineering A, 2011, 528: 8051-8059.
[15] RAGHUNATH B K, RAGHUKANDAN K, KARTHIKEYAN R, PALANIKUMAR K, PILLAI U T S, ASHOK GANDHI R. Flow stress modeling of AZ91 magnesium alloys at elevated temperature[J]. Journal of Alloys and Compounds, 2011, 509(15): 4992-4998.
[16] POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J]. Acta Materialia, 1996, 44(1): 127-136.
[17] 欧阳德来, 鲁世强, 黄 旭, 雷力明. TA15钛合金β区变形动态再结晶的临界条件[J]. 中国有色金属学报, 2010, 20(8): 1539-1544.
OUYANG De-lai, LU Shi-qiang, HUANG Xu, LEI Li-ming. Critical conditions of dynamic recrystallization during deformation of β area in TA15 titanium alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(8): 1539-1544.
[18] 鲁世强, 王克鲁, 李 鑫, 刘诗彪. 一种模拟和预测金属锻造过程动态再结晶的新方法[J]. 金属学报, 2014, 50(9): 1128-1136.
LU Shi-qiang, WANG Ke-lu, LI Xin, LIU Shi-biao. A new method for simulating and predicting dynamic recrystallization in metal forging[J]. Acta Metallurgica Sinica, 2014, 50(9): 1128-1136.
[19] 孙朝阳, 栾京东, 刘 赓, 李 瑞, 张清东. AZ31镁合金热变形流动应力预测模型[J]. 金属学报, 2012, 48(7): 853-860.
SUN Chao-yang, LUAN Jing-dong, LIU Geng, LI Rui, ZHANG Qing-dong. Predicted constitutive modeling of hot deformation for AZ31 magnesium alloy[J]. Acta Metallurgica Sinica, 2012, 48(7): 853-860.
[20] REN Ling-bao, WU Jing, QUAN Gao-feng. Plastic behavior of AZ80 alloy during low strain rate tension at elevated temperature[J]. Materials Science and Engineering A, 2014, 612: 278-286.
[21] SELLARS C M, WHITEMAN J A. Recrystallization and grain growth in hot rolling[J]. Metal Science, 1979, 13(3): 187-194.
(编辑 王 超)
基金项目:河南省基础与前沿技术研究项目(112300413227)
收稿日期:2014-10-27;修订日期:2015-06-15
通信作者:陈拂晓,教授,博士;电话:0379-65627265;E-mail:chenfx126@126.com