J. Cent. South Univ. (2020) 27: 2017-2031

DOI: https://doi.org/10.1007/s11771-020-4427-6

Isothermal diffusion of water vapor in unsaturated soils based on Fick’s second law

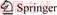
LIU Fei-fei(刘飞飞)¹, MAO Xue-song(毛雪松)¹, ZHANG Jian-xun(张建勋)¹,WU Qian(吴谦)¹, LI Ying-ying(李颖颖)^{1, 2}, XU Cheng(许铖)¹

1. School of Highway, Chang’an University, Xi’an 710064, China;

2. Luoyang Rail Transit Group Co., Ltd., Luoyang 471023, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: In arid regions, water vapor diffusion predominates the total water migration in unsaturated soil, which significantly influences agriculture and engineering applications. With the aim of revealing the diffusion mechanism of water vapor in unsaturated soil, a water vapor migration test device was developed to conduct the water vapor migration indoor test. The test results demonstrate that the characteristics of water vapor diffusion in unsaturated soil conformed to Fick’s second law. A mathematical model for water vapor diffusion under isothermal conditions in unsaturated soil was established based on Fick’s law. Factors including the initial moisture content gradient, initial moisture content distribution, soil type and temperature that affect the water vapor diffusion coefficient were analyzed. The results show that there was good agreement between the moisture content calculated by the mathematical model and obtained by the indoor experiment. The vapor diffusion coefficient increased with increasing initial moisture content gradient and temperature. When the initial moisture content gradient is constant, the vapor diffusion coefficient increases with the increase of matrix suction ratio in dry and wet soil section. The effect of soil type on the water vapor diffusion coefficient was complex, as both the moisture content and soil particle sizes affected the water vapor diffusion.

Key words: water vapor diffusion coefficient; unsaturated soil; mathematical model; initial moisture content gradient; initial moisture content distribution; soil type; temperature

Cite this article as: LIU Fei-fei, MAO Xue-song, ZHANG Jian-xun, WU Qian, LI Ying-ying, XU Cheng. Isothermal diffusion of water vapor in unsaturated soils based on Fick’s second law [J]. Journal of Central South University, 2020, 27(7): 2017-2031. DOI: https://doi.org/10.1007/s11771-020-4427-6.

1 Introduction

Moisture migration in unsaturated soil includes liquid water migration and water vapor diffusion. For soil in arid regions, water vapor diffusion may account for the majority in total moisture migration, considering that the low annual rainfall, deep groundwater level and strong evaporation in these areas [1-4]. For subgrade soil, water vapor migration will cause water to accumulate at the top of the subgrade [5, 6], and further cause the strength decay of the subgrade soil [7-13]. Consequently, for unsaturated soil, it is urgent to investigate the characteristics of water vapor migration.

The main driving force for water vapor migration is generally considered to be the water vapor pressure gradient. Under equilibrium conditions, the water vapor pressure in the soil depends on the temperature, the concentration of the aqueous solution, and the moisture content of the soil [14-19]. Under non-isothermal conditions,water vapor will migrate from high to low temperature, leading to the evaporation of liquid water in the high temperature region and condensation in the low temperature region [20-23]. Further, it has been proved that under non-isothermal conditions, increasing the temperature gradient will intensify the water vapor migration [24-26].

Under isothermal conditions, vapor pressure gradient in the soil is decided by the moisture content of the unsaturated soil. Water vapor will migrate from high to low moisture content. Further, WANG et al [27] stated that the difference in initial moisture contents between the dry and wet soil is a critical factor affecting water vapor migration.

Early studies have established mathematical model to study water vapor diffusion in the unsaturated soils under non-isothermal conditions and isothermal conditions, it was found that water vapor diffusion coefficient was an indispensable parameter when describing the characteristics of water vapor diffusion in unsaturated soil [3, 28-31]. However, in most mathematical models for the water vapor diffusion, how to obtain the coefficient of water vapor diffusion coefficient remains unclear. For example, SAKAI et al [3] adopted an empiric data onto the diffusion coefficient to solve the unsaturated hydraulic conductivity function of revealing the water vapor diffusion. HE et al [30] set up a numerical model to investigate liquid water and vapor migration, and validated the model by comparing with the freezing experiments performed by MIZOGUCHI; nevertheless, the authors did not clearly list the value of the water vapor diffusion coefficient. Although JACKSON [28] established the mathematical model of water vapor and calculated the diffusion coefficient through experiment, the experiment was mainly aimed at water vapor migration from soil to air, rather than water vapor migration from soil to soil. Likely, model for calculating water vapor diffusion coefficient proposed by JABRO [29] was also mainly about the water vapor movement between the soil and the air.

Previous studies concluded that soil particle size and initial moisture content also had an important effect on the water vapor diffusion [28, 29, 32, 33]. Nevertheless, how soil particles and moisture content affect water vapor migration is still controversial.

The objective of this paper is to explore the characteristics of water vapor diffusion in unsaturated soil and establish a simple mathematical model for water vapor diffusion coefficient in unsaturated soil. For this purpose, a self-developed experimental device was adopted to carry out the water vapor diffusion experiment in unsaturated soil under isothermal conditions. Then the experiment data were employed to validate the model of water vapor diffusion coefficient. Furthermore, the effects of initial moisture content distribution, initial moisture content gradient, soil type and temperature on the diffusion coefficient of water vapor were analyzed. The findings in this paper are beneficial to the numerical calculation of water vapor diffusion in unsaturated soil.

2 Materials and method

2.1 Physical property of test soils

The test soils in this study were loess and sands collecting from Shanxi, China. The physical properties of the test soils are listed in Table 1.

The particle size distribution for the sands was achieved using sieve analysis (ASTM, 2014) [34], while the particle size distribution for the loess was determined using both sieve analysis and hydrometer method (ASTM, 2014; ASTM, 2017) [34, 35], as shown in Figure 1.

2.2 Soil-water characteristic curves (SWCCs) of test soils

Soil-water characteristic curves (SWCC) of the sands and loess were obtained using pressure plate according to ASTM C1699-09 [36]. Then the data obtained by the test was fitted according to Eq. (1) [37] to get the SWCCs (Figure 2).

Table 1 Physical properties for the test soils

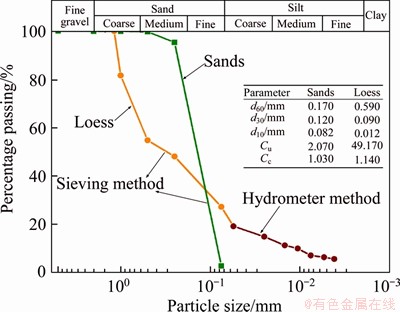
Figure 1 Grain size distributions for test soils

Figure 2 SWCCs for test soils

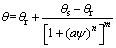                       (1)

where θ is moisture content (%); θ_s and θ_r are saturated and residual moisture contents (%), respectively; ψ=u_a-u_w is the matrix suction (kPa); α, n and m are parameters, and m=1-1/n.

As shown in Figure 2, the SWCC of loess lies above that of sands, suggesting that loess has a stronger water-holding capacity than sands, which may be due to the fact that the loess particle is finer that the sand particle. Research by ZHANG et al [37] also showed that finer particles have a stronger water-holding capacity [38, 39].

2.3 Test apparatus

To investigate the vapor water diffusion in unsaturated soil under isothermal conditions, a vapor water diffusion device was developed (as shown in Figure 3). The test device consists of a soil sample zone, a vapor water diffusion zone, sealing joints, and sealing ends. The soil sample zone consisted mainly of two sections of PVC pipe (length, 100 mm; inner diameter, 50 mm). The right PVC pipe was used to fill the soil with relatively greater moisture content, and it was defined as the wet soil column; while the left PVC pipe was used to fill the soil with relatively lower moisture content, and it was defined as the dry soil column. When the two sections of PVC pipe were connected, a 5 mm air strip was left in the middle to prevent direct contact between the wet and dry soil, so that the moisture from the wet soil section can only migrate to the dry soil in vapor phase, thus creating a vapor water diffusion zone. To prevent soil particles from spilling out of the sample area and to ensure free exchange of gases, the end of the soil sample zone was secured with a fine sieve. To explore the characteristic of water vapor diffusion at different temperatures, an environmental chamber was employed to control the temperature of the soil.

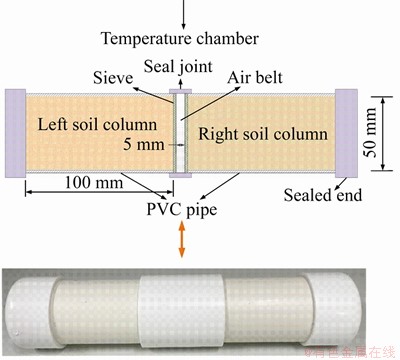
Figure 3 Test apparatus for water vapor diffusion in unsaturated soil

2.4 Test scheme

Previous analysis showed that the primary factors affecting the water vapor diffusion in the unsaturated soil are moisture content, soil type and temperature, time, water content. Therefore, several PVC specimens (as illustrated in Table 2) were prepared to explore the impact of the moisture content gradient, moisture content distribution, soil type and temperature on the water vapor diffusion. In this paper, the difference between the initial moisture content of wet and dry soil columns was defined as the moisture content gradient of the specimen.

Table 2 Specimen information

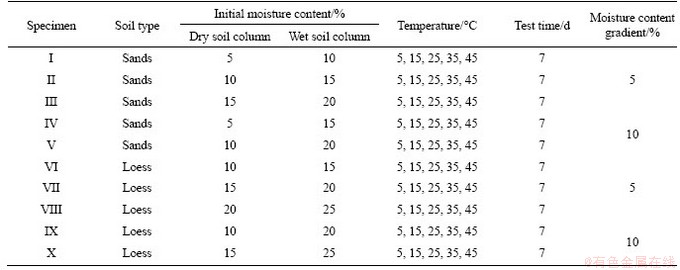
As illustrated in Table 2, to research the effect of the initial moisture content distribution on the water vapor diffusion, specimen groups (I, II, III), (IV, V), (VI, VII, VIII), (IX X) were compared respectively. These specimens in each group have the same initial moisture content gradient, but their moisture content distributions are different.

To research the effect of moisture content gradient on the water vapor diffusion, specimen groups (I, IV), (II, V), (VI, IX), (VII, X) were compared, respectively. These specimens in each group have the same initial moisture content in the dry soil columns, but their moisture content gradients are different.

To compare the vapor water diffusion in loess and sandy soil, specimen groups (II, VI), (III, VII), (V, IX) were selected for comparative study. These specimens in each group have the same initial moisture content distribution.

To explore the impact of temperature on the water vapor diffusion, all the specimens were tested under the temperature of 5, 15, 25, 35 and 45 °C, respectively.

2.5 Test procedure

The test procedure is shown in Figure 4. First, the sands soil samples with the moisture content of 5%, 10%, 15% and 20%; loose soil samples with moisture content of 10%, 15%, 20% and 25% were prepared, respectively. In order to make the moisture content of the soil samples evenly distributed, prepared soil samples were placed in a closed container for 24 h. Then the actual moisture contents of the soil samples were obtained by microwave oven heating method [40].

Fill the prepared soil to the PVC pipes. The ends of the soil columns were fixed with fine sieves. The soil columns were combined according to Table 2. Special attention should be paid to the sealing of the specimens to ensure that the specimens are impermeable in the process of making the test specimens. Afterwards, the specimens were placed in a temperature chamber to ensure that the water vapor migration test is carried out at a constant temperature. After reaching the predetermined test time, the specimens were taken out and cut every 5 cm. Then the moisture contents of each part of soil were measured by microwave oven heating method [40].

3 Test results and analysis

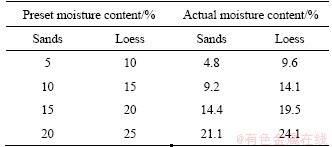
It must be pointed out that the actual measured initial moisture content of the soil column is slightly different from the preset value, as listed in Table 3.

Figure 5 indicates the water content distribution before and after the water vapor diffusion test (7 d). The dotted line represents the initial moisture content distribution of the soil column, while the solid line represents the moisture content distribution of the soil column after the test.

As shown in Figure 5, after 7 days’ test, the moisture content of the wet soil column decreased compared with the initial state; on the contrary, the moisture content of the dry soil column increased. This phenomenon indicates that the water in the wet soil column migrated to the dry soil column in the form of vapor phase. Besides, it is worth noting that the total decreasing water in the wet soil column was slightly larger than the total increasing water in the dry soil column. This may be due to the fact that a small part of the water was adsorbed on the PVC pipe in the form of water droplets, and did not migrate to the dry soil column.

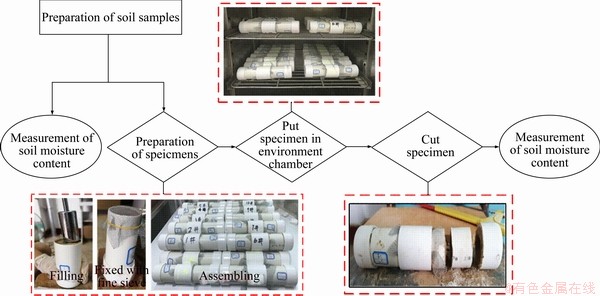
Figure 4 Test procedure

Table 3 Actual initial moisture content of soil samples

It can be seen from Figure 5 that the water vapor diffusion in the different specimens varys greatly although the moisture content gradients are the same. As shown in Figure 5(a), the increasing amplitude of the moisture content (△w, %) for specimen III was larger than the other two specimens; while in Figure 5(c), △w for specimen VI was the largest. Figure 5 also shows that the soil closer to the air belt experienced a larger moisture content variation. For the sands, for example, specimen II (Figure 5(a)), the increasing amplitude of the moisture content (△w) located at 9.5 cm was 12.98 times that located at 0 cm; while for specimen V (Figure 5(b)), the difference in △w between the position of 9.5 cm and 0 cm was relatively smaller, and the former was 4.94 times that of the latter. For the loess, for example, specimen VIII, △w at the position of 9.5 cm was 2.50 times that at the position of 0 cm; while for specimen X, △w at the position of 9.5 cm was 5.69 times that at the position of 0 cm. This phenomenon was consistent well with the material diffusion characteristic described by Fick’s second law, that is, the diffusion concentration of a substance becomes smaller as the diffusion distance increases [41], and even at infinity, the diffusion concentration of a substance is zero.

Figure 5 also shows that the moisture content variation due to the water vapor diffusion affected by the initial moisture content gradient. On the whole, △w of the specimens with 5% moisture content gradient (w_m) was smaller than that with 10% w_m. For the sands soil, when the initial moisture content of the dry soil column (w₀) was 10%, the maximum △w for the specimen V (10% w_m) was 30.42%, while the maximum △w for the specimen II (5% w_m) was 11.68%, the former was 2.61 times the latter. For the loess soil, △w also increased with w_m. For example, the maximum △w for the specimen X (10% w_m) was 1.38 times that for specimen VII (5% w_m). Similarly, when the initial moisture content of the wet soil column (w_s1) was the same, water vapor migration was more intense in the specimen with a drier soil column. Therefore, the initial moisture content gradient (w_m) has an important influence on the moisture vapor diffusion of sand and loess soils, and the water vapor diffusion increases with the increase of the moisture content gradient (w_m).

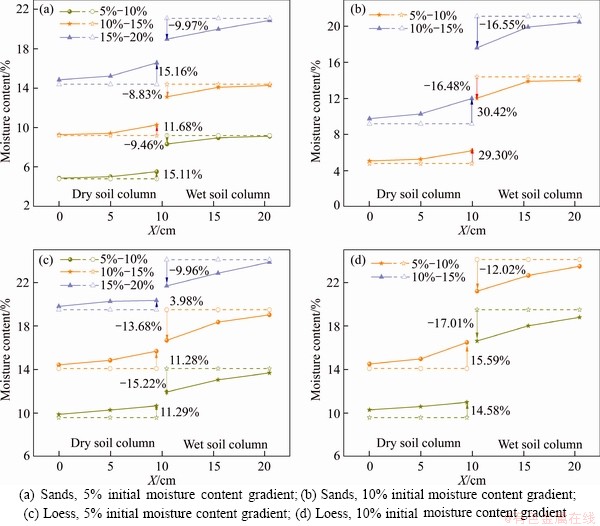
Figure 5 Moisture content before and after water vapor diffusion:

4 Mathematical model for water vapor diffusion coefficient

4.1 Establishment of mathematical model

Fick’s second law [41] was adopted to describe the water vapor diffusion in this work, as shown in Eq. (2). Fick’s second law describes the diffusion of gas from a higher to a lower concentration under the driving force of concentration gradient. The concentration of the gas changes not only with the position but also with the development of the diffusion time, which is in consistent with the nature of water vapor diffusion in this work.

                             (2)

where D is the diffusion coefficient (cm²/s), and water vapor with a greater D means a stronger diffusion ability; C is water vapor concentration (g/cm³); x is the migration distance in the soil (cm); t is the diffusion time (s).

For the initial boundary condition: C=C₀ (t=0, x≥0); C=C_s (t>0, x=0), the special solution of Eq. (2) is shown in Eq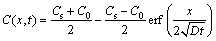. (3)

          (3)

where C (x, t) refers to the concentration of water vapor at time t and at a distance of x from the starting end (g/cm³), D is the water vapor diffusion coefficient (cm²/s), and erf is the error function.

If C (x, t) is known, then the diffusion coefficient D is shown in Eq. 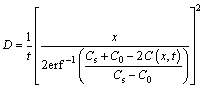(4).

           (4)

To explain the calculation method of water vapor diffusion coefficient in this paper, the coordinate position of the soil column was defined, as shown in Figure 6.

Figure 6 Horizontal position coordinate diagram of soil column (unit: cm)

In the soil, the concentration of water vapor refers to the water vapor density (ρ_v). Taking the section of the dry soil column located at 9 cm as an example, C₀ shown in Eqs. (5) and (6) is the initial water vapor density in the dry soil column (ρ_v0).

Since the soil located at 10.5 cm directly supplies water vapor to the drier soil, C_s shown in Eqs. (5) and (6) is the water vapor density in the soil located at 10.5 cm (ρ_vs), and it is always changing with the water vapor diffusion time t. In this paper, for the soil located at 10.5 cm, the average value of the initial water vapor density and the water vapor density at time t is taken as ρ_vs. Likewise, C(x, t) in Eqs. (5) and (6) is the water vapor density at position x and at time t (ρ(x, t)). Hence, Eq. (6) can be changed to Eq. 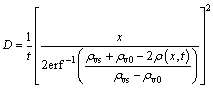(5).

          (5)

The water vapor density in the soil (ρ_v) can be obtained by Eq. (6).

                              (6)

where ρ_v is the water vapor density (kg/m³); ω_v is the molar mass of water vapor and its value is 18 kg/kmol; u_v is the partial pressure of water vapor (kPa); R is the universal gas constant, and its value is 8.314×10^-3 kJ/(mol·K); T is the thermodynamic temperature (K), among which, the partial pressure of water vapor (u_v) can be calculated out by Eq. 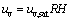(7).

                              (7)

where u_v,sat is the saturated vapor pressure of water (kPa), and RH is the air relative humidity in the soil. The saturated water vapor pressure u_v,sat is closely related to thermodynamic temperature T [42], as shown in Eq. (8).

             (8)

It should be noted that currently, it is difficult to directly test the air relative humidity in the soil. Therefore, indirect methods are usually used to obtain the air relative humidity in the soil, among which, Calvin equation, proposed by Lord Kelvin in 1871 [43], is one of the indirect methods for obtaining the air relative humidity in the soil, as shown in Eq. (9).

                      (9)

where u_a-u_w is the matrix suction of soil (kPa); v_w is the partial molar volume of water vapor (m³/mol); R and T are shown in Eq. (6).

Then adjust Eq. (9) to get Eq. (10),

                  (10)

Bring Eqs. (7), (8) and (10) into Eq. (6),

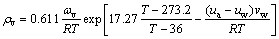 (11)

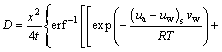
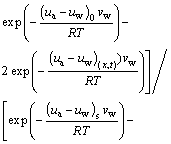
Bring Eq. (11) into Eq. (5) to get Eq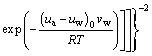. (12),

            (12)

where (u_a-u_w)₀ is the initial matric suction of the dry soil column (kPa); (u_a-u_w)_s is the matric suction of the soil located at 10.5 cm (kPa), and it is the average value of the initial matric suction ((u_a-u_w)_s1 ) and the matric suction at time t ((u_a-u_w)_s2 ); (u_a-u_w)_(x,t) is the matric suction of soil at the position x and at time t.

The matric suction of the unsaturated soil is directly related to its moisture content, as illustrated in Figure 2. Therefore, D_t can be calculated out by measuring the initial moisture content for the dry soil column (w₀), the wet soil column (w_s1), the soil located at 10.5 cm when the time is t (w_s2), and the soil at position x, time is t (w_(x,t)).

4.2 Calculation and verification of water vapor diffusion coefficient

Taking the section of the dry soil column located at 9.5 cm as an example, x is 1 cm. When the water vapor diffusion time (t) is 7 d, the water vapor diffusion coefficients for the test soils calculated by Eq. (12) are shown in Tables 4 and 5, respectively.

In order to verify D_t listed in Tables 4 and 5, the moisture contents of soil located at 0 cm and 5 cm were calculated. When x is 0 cm and 5 cm, (u_a-u_w)_(x,t) can be calculated by bringing D_t into Eq. (12). Then the calculated moisture content can be obtained by bringing the calculated (u_a-u_w)_(x,t) into Figure 2. Finally, the calculated data were compared with the test one to verify D_t (see Figure 7).

As shown in Figure 7, the curves for the calculated moisture content are extremely close to the curves for the actual measured moisture content, indicating that the calculation moisture content agrees fairly well with the measured one. Therefore, the calculation method for the water vapor diffusion coefficient (D) proposed in this paper is reasonable. Also, Fick’ second law can well reflect the diffusion behavior of water vapor in the soil. It is worth noting that the test moisture content is slightly larger than the calculated one. This may be because that during the test, slightly liquid water migration occurred, due to the tight contact between soil and soil in the dry soil column. And calculation in this paper only considered the migration of water vapor, ignoring the migration of liquid water.

Table 4 Diffusion coefficient D_t for sands

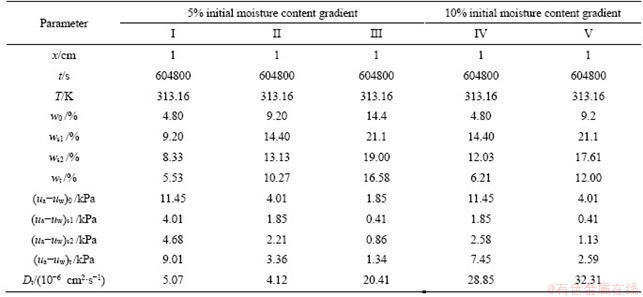
Table 5 Diffusion coefficient D_t for loess

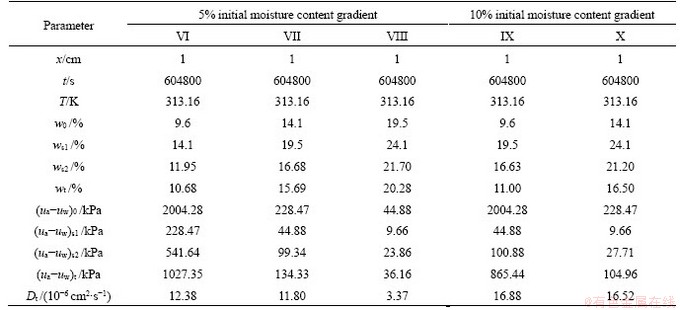
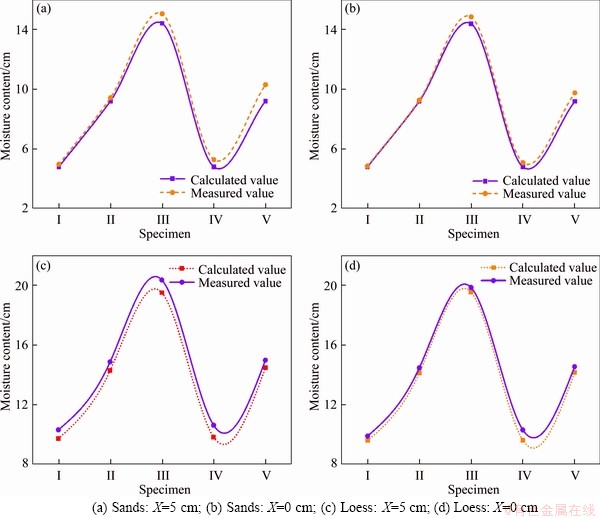
Figure 7 Comparison between calculated and test moisture content:

5 Factors affecting water vapor diffusion coefficient

5.1 Effect of initial moisture content gradient on water vapor diffusion coefficient

Figure 8 shows that the water vapor diffusion coefficients (D) of each specimen are different. In general, when w₀ is certain, D for the specimen with 10% w_m is generally greater than that with 5% w_m. For the sands, D for the specimen V (10%-20%) was 32.31×10^-6 cm²/s, which was the largest among the five specimens; while specimen II (10%-15%) had the smallest water vapor diffusion coefficient. For the loess, D for specimen IX (15%-25%) was 16.88×10^-6 cm²/s, which was 1.43 times of that for specimen VII (15%-20%).

This may be due to the fact that the thickness of the water film increases when the moisture content increases, and then the adsorption effect of the soil particle on the outermost water film decreases. As a result, the outermost water film is more susceptible to release from the soil particles, converts the phase into water vapor, and increases the water vapor density between the soil particles. When w₀ is constant, the water vapor concentration gradient between the dry soil column and the wet soil column is greater in the specimen with a wetter soil column. Similarly, when w_s1 is constant, the water vapor concentration gradient between the dry soil column and the wet soil column is greater in the specimen with a drier soil column. Furthermore,the adsorption capacity of soil particles to water increases with the decrease of moisture content, due to the fact that the matrix suction increases with the decrease of moisture content (see Figure 2). And this will increase the diffusion of water vapor. All in all, a greater w_m makes the water vapor diffusion more intense, resulting in a larger water vapor diffusion coefficient.

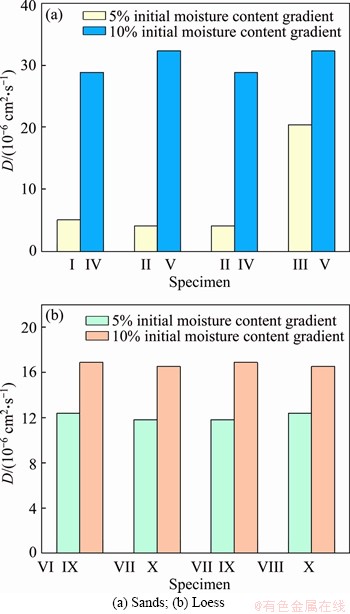
Figure 8 Effect of initial moisture content gradient on diffusion coefficient:

5.2 Effect of initial moisture content distribution on water vapor diffusion coefficient

As shown in Figure 9, specimens with different initial moisture contents have significantly different water vapor diffusion coefficients (D), even under the same initial moisture content gradient. For the sands soil, when w_m was 5%, D for specimen III (15%-20%) was the largest; when w_m was 10%, D for specimen V (10%-20%) was larger than that for specimen IV (5%-15%). On the surface, it shows that the specimen with the wettest soil column has the greatest vapor water diffusion coefficient (D).

Figure 9(b) shows that when w_m was 5%, D for specimen VI (10%-15%) was the largest, although w_s1 for specimen VI (10%-15%) was the smallest among the three specimens. Further, when w_m was 10% (10%-20%), D for specimen IX (10%-20%) was slightly larger than that for specimen X (15%-25%); while w_s1 for the former was smaller than that for the latter. D did not increase as w_s1 increased. This phenomenon means that the value of water vapor diffusion coefficient (D) is not only depending on the moisture content in the wet soil column or the dry soil column.

Figure 9 Effect of initial moisture content distribution on diffusion coefficient:

It can be observed in Eq. (12) that when the temperature (T), the diffusion time (t), and the calculated position (x) are constant, D is affected by the soil matrix suction of the dry and wet soil column. The ratio of matrix suction between the wet soil column and the dry soil column (R_ms) under the initial state is plotted in Figure 9. It was found that for the same kind of soil, the development trend of D was consistent with the development trend of R_ms. That is, the specimen with a larger D also had a greater R_ms. For example, for the sands, when w_m was 5%, R_ms for specimen III (10%-20%) was the largest among the three specimens, and D for specimen III was also the largest. Similarly, for the loess soil, R_ms for specimen IX (10%-20%) was much higher than that for specimen X (15%-20%), so D for the former was larger.

Consequently, under the same initial moisture content gradient, water vapor diffusion coefficient could not be determined by comparing the initial moisture content at one end of the soil column, and it is determined by the ratio of soil matrix suction between the dry soil column and wet soil column.

5.3 Effect of soil type on water vapor diffusion coefficient

Figure 10 shows that D for the sand is quite different from that for the loess, although the initial moisture content distribution is the same. When the initial moisture content distribution was 10%-15%, D for the sands (specimen II) was 4.12×10^-6 cm²/s, while D for the loess (specimen VI) was 12.38× 10^-6 cm²/s, which was three times that of the former. This may be because that when the moisture content was 10%, the soil matrix suction of the loess was very large (see Figure 2) because the moisture content was much smaller than the optimum moisture content (14.1%). And this led the loess soil particle to have a strong water adsorption capacity. Accordingly, the water vapor diffusion in the loess soil was more severe. Hence, when the initial moisture content distribution was 10%-20%, the water vapor diffusion coefficient for the loess was greater than that for the sands.

Nevertheless, when the initial moisture content distribution was 10%-20% and 15%-20%,respectively, the water vapor diffusion coefficient of the sand was obviously larger than the diffusion coefficient of the loess. Although the loess soil particle had a stronger water adsorption capacity when w₀ was the same, the sands soil particle was more likely to lose water when w_s1 was the same. Hence, the water vapor diffusion coefficient for the loss does not always be larger than that for the sands.

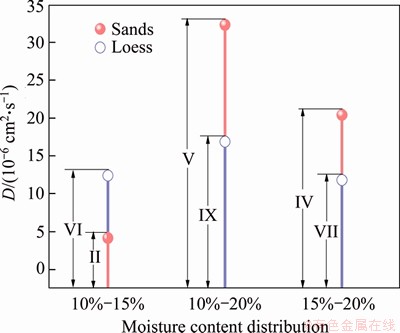
Figure 10 Comparison of water vapor diffusion coefficients between sands and loess

Another factor that affects the water vapor diffusion is the soil particle size. The gradation curves for the sands and loess (see Figure 1) show that the particle size of the sand was greater than that loess on the whole. This leads to a larger porosity and better pore connectivity in the sands soil columns, which provides a convenient channel for the water vapor diffusion and thereby is conducive to the water vapor diffusion. Instead, the porosity in the loess soil column was smaller, the connectivity between the pores was poorer, and the channel through which the water vapor diffuses was rather tortuous, which will hinder the diffusion of water vapor. Therefore, D for the sand was greater than the diffusion coefficient of the loess. The findings agree well with the conclusion obtained by JABRO [29], who investigated the effect of particle size on D and concluded that D increased with the increase in particle size. Similarly, JACKSON [28] also pointed out that D for the soil containing more sand fraction was greater. Furthermore, ZHANG et al [33] concluded that the diffusion rate of water vapor in the sandy loam soil was twice than that of in clay.

Hence, when the initial moisture content distribution is constant, the particle size and moisture content together affect the water vapor diffusion, making it difficult to intuitively conclude that a certain type of soil has a larger water vapor diffusion coefficient. More work needs to carry out to investigate the effect of soil type on the water vapor diffusion coefficient.

5.4 Effect of temperature on water vapor diffusion coefficient

Figure 11 shows that temperature has a large effect on diffusion coefficient of water vapor (D). In general, D increases with increasing temperature in both sands and loess soil column. For example, for the sands specimen V (10%-20%), when the temperature was 45 °C, D was 32.31×10^-6 cm²/s;when the temperature was 5 °C, D was 12.83×10^-6 cm²/s, and the former was 2.52 times the latter. For the loess specimen X, when the temperature was 45 °C, D was 16.52×10^-6 cm²/s; when the temperature was 5 °C, D decreased to 1.21×10^-6 cm²/s, and the former was 5.52 times the latter.

Figure 11 Effect of temperature on diffusion coefficient:

This is due to the fact that the kinetic energy of the water molecules is proportional to the temperature. A higher temperature leads the kinetic energy to increase and in turn increase the velocity of water molecule. As a result, it is easier for the water film to break away from the bound of soil particles and change into water vapor. This leads to a more intense diffusion of water vapor, which eventually leads to a greater D. On the contrary, when the temperature is relatively low, the kinetic energy of the water molecules is quite small, so that it is difficult for the water film to get rid of the adsorption of the soil particles, and finally D is also small. JABRO [29] also concluded that D is positively correlated with temperature.

6 Conclusions

In this paper, isothermal diffusion of water vapor in the unsaturated soil was investigated by laboratory test. A simple mathematical model for calculating the water vapor diffusion coefficient in unsaturated soil was established and verified based on the laboratory test. Furthermore, factors including the initial moisture content gradient, initial moisture content distribution, soil type and temperature that affect the water vapor diffusion coefficient were analyzed. The main conclusions are as follows:

1) A water vapor migration test device was developed, which mainly includes soil sample zone, water vapor diffusion zone, and an end, to analyze the water vapor diffusion characteristics in unsaturated soil. The main feature of the test device is the provision of a vapor diffusion zone, through which only water vapor is allowed to pass.

2) The laws of water vapor diffusion in the unsaturated soils extremely conformed to Fick’s law. A mathematical model for the water vapor diffusion coefficient in unsaturated soil was established based on Fick’s second law. The rationality of the mathematical model was verified by water vapor diffusion test.

3) When the initial moisture content of the wet or dry soil column is constant, specimen with a greater initial moisture content gradient also exhibits a larger difference of matrix suction between dry soil section and wet soil column, making the vapor diffusion coefficient increase with the initial moisture content gradient.

4) When the initial moisture content gradient is constant, a different moisture content distribution results in a different vapor water diffusion coefficient. For the same kind of soil, a larger matrix suction ratio between the dry and wet soil column determines a greater water vapor diffusion.

5) The impact of soil type on the diffusion coefficient of water vapor was complicated, considering that the moisture content and soil particle size together influenced water vapor diffusion.

6) The water vapor diffusion coefficient increased when the temperature increased, because the kinetic energy of the water molecules increased with the increase of the temperature.

Nomenclature

θ

Moisture content

θ_s

Saturated moisture content

θ_r

Residual moisture content

α

Parameter for the SWCC

n

Parameter for the SWCC

D

Water vapor diffusion coefficient

w₀

Initial moisture content of the dry soil column

w_s1

Initial moisture content of the wet soil column

w_m

Initial moisture content gradient

w_s2

Moisture content of the soil located at 10.5 cm when the time is t

w_(x,t)

Moisture content of the soil at the position x, time t

ρ_v

Water vapor density

ω_v

Molar mass of water vapor

u_v

Partial pressure of water vapor

u_v,sat

Saturated vapor pressure of water

R

Universal gas constant

T

Thermodynamic temperature

C(x, t)

Concentration of water vapor at time t and at distance x

u_a-u_w

Matrix suction

(u_a-u_w)₀

Initial matric suction of the dry soil column

(u_a-u_w)_s

Matric suction of the soil located at 10.5 cm

(u_a-u_w)_s1

Initial matric suction of the wet soil column

(u_a-u_w)_s2

Matric suction of the soil located at 10.5 cm, time t

(u_a-u_w)_(x,t)

Matric suction of soil at the position x and at time t

References

[1] MILLY P C D. A simulation analysis of thermal effects on evaporation from soil [J]. Water Resources Research, 1984, 20(8): 1087-1098. DOI: 10.1029/WR020i008p01087.

[2] SCANLON B, KEESE K, REEDY R, SIMUNEK J, ANDRASKI B J. Variations in flow and transport in thick desert vadose zones in response to paleoclimatic forcing (0-90 kyr): Field measurements, modeling, and uncertainties [J]. Water Resources Research, 2003, 39(7): 1179. DOI: 10.1029/2002WR001604.

[3] SAKAI M, TORIDE N, SIMUNEK JIRKA J. Water and vapor movement with condensation and evaporation in a sandy column [J]. Soil Sci Soc Am J, 2009, 73(3): 707-717. DOI: 10.2136/sssaj2008.0094.

[4] SHMUEL A, TAMIR K. Liquid and vapor water in vadose zone profiles above deep aquifers in hyper-arid environments [J]. Water Resources Research, 2019, 55(5): 3619-3631. DOI: 10.1029/2018WR024435.

[5] GUTHRIE W S, HERMANSSON A, WOFFINDEN K H. Saturation of granular base material due to water vapor flow during freezing: Laboratory experimentation and numerical modeling [C]// 13th International Conference on Cold Regions Engineering, 2006: 1-12. DOI: 10.1061/ 40836(210)66.

[6] LIU Fei-fei, MAO Xue-song, XU Cheng, LI Ying-ying, WU Qian, ZHANG Jian-xun. “Covering effects” under diurnal temperature variations in arid and semiarid areas [J]. Advances in Civil Engineering, 2020(5): 1-12. DOI: 10.1155/2020/7496182.

[7] LI Qian. The finite element analysis of covering effect performance of highway asphalt pavement on subgrade in Xinjiang [C]// International Conference on Electric Technology & Civil Engineering, 2011. DOI: 10.1109/ RSETE.2011.5965343.

[8] LI Qing, YAO Yang-ping, HAN Li-ming, HU Jian, PENG Ren, WANG Nai-dong. Pot-cover effect of soil [J]. Industrial Construction, 2014, 44(2): 69-71. DOI: 10. 13204/ j. gyjz201402016. (in Chinese)

[9] ZHANF Sheng, TENG Ji-dong, HE Zuo-yue, LIU Yan, LIANG Si-hao, YAO Yang-ping, SHENG Dai-chao. Canopy effect caused by vapour transfer in covered freezing soils [J]. J Géotechnique, 2016, 66(11): 927-940. DOI: 10.1680/ jgeot.16.p.016.

[10] NIU Fu-jun, LI An-yuan, LUO Jing, LIN Zhan-ju, YIN Guo-an, LIU Ming-hao, ZHENG Hao, LIU Hua. Soil moisture, ground temperatures, and deformation of a high-speed railway embankment in Northeast China [J]. Cold Regions Science and Technology, 2017, 133: 7-14. DOI: https://doi.org/10.1016/j.coldregions.2016.10.007.

[11] GAO Jian-qiang, LAI Yuan-ming, ZHANG Ming-yi, FENG Zi-liang. Experimental study on the water-heat-vapor behavior in a freezing coarse-grained soil [J]. Applied Thermal Engineering Design Processes Equipment Economics, 2018, 128: 956-965. DOI: https://doi.org/10. 1016/j.applthermaleng. 2017.09.080.

[12] BAI Rui-qiang, LAI Yuan-ming, ZHANG Ming-yi, GAO Jian-qiang. Water-vapor-heat behavior in a freezing unsaturated coarse-grained soil with a closed top [J]. Cold Regions Science and Technology, 2018, 155: 120-126. DOI: https://doi.org/10.1016/j.coldregions.2018.08.007.

[13] ZENG Ling, YAO Xiao-fei, ZHANG Jun-hui, GAO Qian-Feng, CHEN Jing-cheng, GUI Yu-tong. Ponded infiltration and spatial-temporal prediction of the water content of silty mudstone[J]. Bulletin of Engineering Geology and the Environment, 2020. DOI: 10.1007/s10064- 020-01880-1.

[14] CARY J W. Soil heat transducers and water vapor flow [J]. Soil Sci Soc Am J, 1979, 43(5): 835-839. DOI: 10.2136/sssaj1979.03615995004300050003x.

[15] LI Shu-xun, CHENG Guo-dong. Problem of heat and moisture transfer in freezing and thawing soils　[M]. Lanzhou: Lanzhou University Press, 1995. (in Chinese)

[16] LI Shuang-yang, NIU Fu-jun LAI Yuan-ming, PEI Wan-sheng, YU Wen-bing. Optimal design of thermal insulation layer of a tunnel in permafrost regions based on coupled heat-water simulation　[J]. Applied Thermal Engineering Design Processes Equipment Economics, 2017, 110: 1264-1273. DOI: https://doi.org/10.1016/j.appltherma leng.2016.09.033.

[17] ZHANG Ming-li, WEN Zhi, DONG Jian-hua, WANG De-kai, HOU Yan-dong, XUE Ke, YANG Xiao-yu, SUN Guo-dong. Coupled water-vapor-heat transport in shallow unsaturated zone of active layer in permafrost regions　[J]. Rock and Soil Mechanics, 2018, 39(2): 561-570. DOI: 10.16285/j.rsm. 2017.1128. (in Chinese)

[18] SVIERCOSKI R F, EFENDIEV Y, MOHANTY B P. Upscaling the coupled water and heat transport in the shallow subsurface [J]. Water Resources Research, 2018, 54: 995-1012. DOI: https://doi.org/10.1002/2017WR021490.

[19] YIN Xiao, LIU En-long, SONG Bing-tang, ZHANG De. Numerical analysis of coupled liquid water, vapor, stress and heat transport in unsaturated freezing soil [J]. Cold Regions Science and Technology, 2018, 155: 20-28. DOI: 10.1016/ j.coldregions.2018.07.008.

[20] PHILIP J R, DEVRIES D A. Moisture movement in porous materials under temperature gradients [J]. Trans Am Geophys Union, 1957, 38(2): 222-232. DOI: 10.1029/ TR038i002p00222.

[21] MIYAZAKI T. Condensation and movement of water vapor in sand under temperature gradient [J]. Transactions of the Japanese Society of Irrigation Drainage & Reclamation Engineering, 1976, 61: 1-8. DOI: 10.11408/jsidre1965. 1976.1.

[22] SHAO W, COENDERS-GERRITS M, JUDGE J, ZENG Yi-jian, SU Ye. The impact of non-isothermal soil moisture transport on evaporation fluxes in a maize cropland [J]. Journal of Hydrology, 2018, 561: 335-347. DOI: https://doi.org/ 10.1016/j.jhydrol.2018.04.018.

[23] MA Hong-yun, YANG Qing-chun, YIN Li-he, HUANG Jin-ting, ZHANG Jun, WANG Xiao-yong, LI Chen-zhu. Isotopic implications for vapor-liquid infiltration pattern in the desert area of ordos plateau, China [J]. Clean-Soil, Air, Water, 2017, 45(5): 1500718. DOI: 10.1002/clen.201500718.

[24] HE Zai-qiu, WANG Tie-hang, ZHAO Shu-de. Coupling calculation method for the transfer of water vapor and liquid water in unsaturated soil [J]. Journal of Xi'an University of Architecture & Technology, 2004(3): 285-287+298. DOI: 10.15986/j.1006-7930.2004.03.006. (in Chinese)

[25] LI Yan-long, WANG Jun, WANG Tie-hang. Moisture migration of unsaturated soil due to thermal gradients [J]. Rock and Soil Mechanics, 2016, 37(10): 2839-2844. DOI: 10.16285/j.rsm.2016.10.014. (in Chinese)

[26] BAI Rui-qiang, LAI Yuan-ming, ZHANG Ming-yi, REN Jing-ge. Study on the coupled heat-water-vapor-mechanics process of unsaturated soils [J]. Journal of Hydrology, 2020, 585: 124784. DOI: 10.1016/j.jhydrol.2020.124784.

[27] WANG Ming-wu, LI Jian, GE Song, QIN shuai, XU Peng. An experimental study of vaporous water migration in unsaturated lime-treated expansive clay [J]. Environmental Earth Sciences, 2015, 73(4): 1679-1686. DOI: 10.1007/ s12665-014-3520-2.

[28] JACKSON R D. Water vapor diffusion in relatively dry soil: I. theoretical considerations and sorption experiments1[J]. Soil Science Society of America Journal, 1964, 28(2): 172-176. DOI: 10.2136/sssaj1964.0361599500280002001 4x.

[29] JABRO J D. Water vapor diffusion through soil as affected by temperature and aggregate size [J]. Transport in Porous Media, 2009, 77(3): 417-428. DOI: 10.1007/s11242-008- 9267-z.

[30] HE Zuo-yue, ZHANG Sheng, TENG Ji-dong, YAO Yang-ping, SHENG Dai-chao. A coupled model for liquid water-vapor-heat migration in freezing soils [J]. Cold Regions Science and Technology 2018, 148. DOI: 10.1016/j.coldregions.2018.01.003.

[31] SHAO W, SU Y, LANGHAMMER J. Simulations of coupled non-isothermal soil moisture transport and evaporation fluxes in a forest area [J]. Journal of Hydrology and Hydromechanics, 2018, 66(4): 410-425. DOI: 10.1515/ johh-2017-0038.

[32] WANG Nai-dong, MA Zi-qi, YAO Yang-ping, JIA Jun-feng, CHEN Han, LI Cheng-zhi. Analysis of moisture migration affected by test period and initial water content [J]. Industrial Construction, 2016, 46(9): 13-16. DOI: 10.13204/ j.gyjz201609004. (in Chinese)

[33] ZHANG CY, ZHAO Y D, ZHANG R R, ZHENG Y L. Research on the influence of water vapor diffusion and evaporation on water and heat transfer in frozen soil [J]. Eurasian Soil Science, 2018, 51(10): 1240-1251. DOI: 10.1134/ S1064229318100150.

[34] ASTM C136/C136M-14. Standard test method for sieve analysis of fine and coarse aggregates [S]. West Conshohocken, PA: ASTM International, 2014. DOI: 10.1520/C0136_C0136M-14.

[35] ASTM D7928-17. Standard test method for particle-size distribution (Gradation) of fine-grained soils using the sedimentation (Hydrometer) analysis [S]. West Conshohocken, PA: ASTM International, 2017. DOI: 10.1520/D7928-17.

[36] ASTM C1699-09(2015). Standard test method for moisture retention curves of porous building materials using pressure plates [S]. West Conshohocken, PA: ASTM International, 2015. DOI: 10.1520/C1699-09R15.

[37] van GENUCHTEN T M. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. DOI: 10.2136/sssaj1980.0361599500440005000 2x.

[38] ZHANG Jun-hui, PENG Jun-hui, LIU Wei-zheng, LU Wei-hua. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction [J]. Road Materials and Pavement Design, 2019. DOI: 10.1080/ 14680629.2019.1651756.

[39] PENG Jun-hui, ZHANG Jun-hui, LI Jue, YAO Yong-sheng, ZHANG An-shun. Modeling humidity and stress-dependent subgrade soils in flexible pavements [J]. Computers and Geotechnics, 2020, 120: 103413. DOI: 10.1016/j.compgeo. 2019.103413.

[40] ASTM D4643-17. Standard test method for determination of water content of soil and rock by microwave oven heating [S]. West Conshohocken, PA: ASTM International, 2017. DOI: 10.1520/D4643-17.

[41] KAUFMANN R S. Fick’s law [M]. Netherlands: Springer, 1998.

[42] TETENS O. Uber einige meteorologische Begriffe [J]. Zeitschrift Geophysic, 1930, 6: 297-309. https://www. researchgate.net/publication/290164955.

[43] THOMSON W. On the equilibrium of vapour at a curved surface of liquid [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1871, 42(282): 448-452. DOI: 10.1080/14786447108640606.

(Edited by HE Yun-bin)

中文导读

基于Fick第二定律的非饱和土中汽态水等温扩散研究

摘要：干旱地区非饱和土中汽态水扩散是水分迁移的主要组成部分，这对农业和工程应用具有重要影响。为了揭示非饱和土中汽态水扩散机理，研制了汽态水扩散试验装置，进行了非饱和土汽态水扩散室内试验。试验结果表明非饱和土中汽态水扩散特性符合Fick第二定律。基于Fick定律，建立了等温条件下非饱和土汽态水扩散的数学模型，分析了初始含水率梯度、初始含水率分布、土体类型和温度等因素对汽态水扩散系数的影响。结果表明：用所建的数学模型计算的含水率与室内试验结果吻合较好；汽态水扩散系数随着初始含水率梯度和温度的增加而增大；在初始含水率梯度一定的条件下，汽态水系数随着这干土段和湿土段基质吸力比值的增大而增大；含水率和土颗粒粒径均对汽态水扩散系数有所影响，致使土体类型对汽态水扩散系数的影响比较复杂。

关键词：汽态水扩散系数；非饱和土；数学模型；初始含水率梯度；初始含水率分布；土的类型；温度

Foundation item: Projects(51878064, 51378072) supported by the National Natural Science Foundation of China; Projects(300102218408, 300102219108) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2020-05-18; Accepted date: 2020-06-05

Corresponding author: MAO Xue-song, PhD, Professor; Tel: +86-18192830325; E-mail: xuesongxian@aliyun.com; ORCID: 0000- 0003-2325-7661