Trans. Nonferrous Met. Soc. China 23(2013) 180-192

First-principles thermodynamics of metal-oxide surfaces andinterfaces: A case study review

Yong JIANG^1,2, Can-hui XU^1,2, Guo-qiang LAN^1,2

1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. Key Laboratory of Nonferrous Materials Science and Engineering, Ministry of Education, Central South University, Changsha 410083, China

Received 10 November 2012; accepted 11 December 2012

Abstract: An important step for achieving the knowledge-based design freedom on nano- and interfacial materials is attained by elucidating the related surface and interface thermodynamics from the first principles so as to allow engineering the microstructures for desired properties through smartly designing fabrication processing parameters. This is demonstrated for SnO₂ nano-particle surfaces and also a technologically important Ag-SnO₂ interface fabricated by in-situ internal oxidation. Based on defect thermodynamics, we first modeled and calculated the equilibrium surface and interface structures, and as well corresponding properties, as a function of the ambient temperature and oxygen partial pressure. A series of first principles energetics calculations were then performed to construct the equilibrium surface and interface phase diagrams, to describe the environment dependence of the microstructures and properties of the surfaces and interfaces during fabrication and service conditions. The use and potential application of these phase diagrams as a process design tool were suggested and discussed.

Key words: metal oxide; surface phase diagram; interface phase diagram; equilibrium crystal shape; first-principles; thermodynamics

1 Introduction

Metal oxides show a vast variety of properties, from insulators to semiconductors, to electronic conductors or even superconductors. The applications are equally diverse. Examples of recent applications include transparent conducting oxides as electrodes for photovoltaics [1], high-K oxides for CMOS, DRAM or flash memories [2], nanostructured ferroelectric and multiferroic oxides for spintronic devices [3], semiconducting and conducting oxides for thin film transistors [4], dielectric oxides for energy storage purposes [5], and etc. Particularly, the surfaces of metal oxides can exchange charges with a wide variety of adsorbed organic molecules [6], which renders them useful in novel organic electronics [7] and chemical catalysis [8]. Recently, the interfaces of metal oxides with metals have also become a hot research topic, for they dictate the integrity and reliability of many material systems, ranging from macroscale structural composites [9], to functional thin-films and coatings [10], as well as nanoscale electronic devices [11].

Metal oxide surfaces and interfaces have attracted considerable research attention in recent years not only because of their unique properties and many novel applications but also because of their fundamental interest. The metal oxide surfaces are complicated by the fact that the low-index planes are often polar, so that the clean, bulk-terminated crystal surfaces may have divergent electrostatic surface energies. Charge compensation mechanisms that lead to a finite dipole may result in important modifications of the surface geometric and electronic structure, including changes in the valence state of surface ions, surface reconstructions, surface roughening and faceting, among others. As the result, the microstructures (and hence the properties) of the surfaces vary with ambient environmental conditions under fabrication and service conditions [12]. For example, tin dioxide (SnO₂) is a wide band-gap semiconductor with an interesting combination of low electrical resistance and high optical transparency, and has been widely used in applications such as solar cells, flat panel displays, touch controls, and defrosting windows [13,14]. Recently, it is found that oxygen chemistry of SnO₂ surfaces sensitively relies on the ambient environmental atmosphere which has been reflected by the measurable change of electrical conductivity [15], making it also attractive for new applications including oxidation catalysts and gas sensors [16]. Moreover, nanofabricated SnO₂ was suggested as a promising alternative to the conventional anode materials in lithium-ion batteries [17], due to its high capacity as well as the low active voltage. In this application, the anode performance is closely related to the surface quality and stability of SnO₂ nanoparticles. Undoubtedly, a fundamental understanding of these environment-microstructure-property interactions would be an essential component in the smart design and engineering context of SnO₂ surfaces in these applications.

The interfaces of SnO₂ with metals, such as Ag, are also technologically important. Such interfaces widely present in oxide dispersion-strengthened (ODS) Ag alloys which constitute an important group of composite materials uniquely characterized with both improved strength and high thermal/electrical conductivity at elevated temperatures [18]. In the case of electrical contact materials, the ODS Ag-SnO₂ alloy is the most promising alternative to the traditional Ag-CdO alloy [19-23]. These alloys are now often fabricated through in-situ internal oxidation of dilute alloy powders. The performance and reliability of these alloys are largely determined by the microstructure and properties of the internal metal-metal-oxide interfaces, which in turn, are dictated by internal reaction thermodynamic conditions and can also be significantly affected by a trace amount of impurities. The fundamentals governing these interface-related mechanisms and interrelations have been exemplarily clarified for the ODS Cu-Al₂O₃ alloy [9], and need also be understood for the ODS Ag-SnO₂ alloy.

It is prohibitive to rely solely on experiments to systematically explore such fundamental interrelations and mechanisms. The first-principle calculations have emerged as an indispensable tool in recent years, being able to single out influence factors and phenomenology correlated to the considered application, to provide many useful insights from an improved basic understanding of surface and interface thermodynamics and even defect and impurity effects. The protocol that allows such calculations to provide insights has been illustrated for CeO₂ and SnO₂ surfaces [12,24], and Ni-Al₂O₃ and Cu-Al₂O₃ interfaces [9,10,25,26].

In this work, we employ the same first-principles based calculations to investigate SnO₂ surfaces and an Ag-SnO₂ interface. From the concepts of first-principles thermodynamics, we first expressed the surface energy of SnO₂ as a direct function of temperature (T) and oxygen partial pressure p_O2, and extended our DFT investigations to all non-stiochiometric (both Sn- and O-terminated) surfaces of (110), (101), and (100). This approach enabled us to construct the equilibrium surface phase diagram to predict and compare surface stabilities of SnO₂ under more practical environmental conditions, i.e., for any given T and p_O2. Moreover, the results can be further utilized to predict the thermal equilibrium morphology of SnO₂ nano-particles, based on the Gibbs–Wulff theorem of equilibrium crystal shape (ECS). For the internally oxidized Ag-SnO₂ interface, we first performed high-resolution transmission electron microscopy (HRTEM) to determine the basic orientation relation of SnO₂ in Ag matrix, based on which we proposed various atomistic models for possible interface structures with considering different stoichiometry/ termination and coordination types. The associated free energies and properties (adhesion strength, wettability, and relative stabilities) were then evaluated from ab initio calculations, as a function of ambient temperature and oxygen partial pressure. These data were then used to construct the equilibrium interface phase diagram, through which we can describe the environment- microstructure-property relations of the internal interfaces during the process of internal oxidation.

2 Computational methods

All the first-principle calculations were based on density functional theory [27,28] as implemented in a plane-wave, pseudopotential code VASP (Vienna ab initio simulation package) [29]. The ion-electron interaction was described by the projector augmented wave method (PAW) [30] within the frozen-core approximation. To sample the Brillouin zone, the k-meshes were generated automatically using the Monkhorst–Pack method [31]. The electronic minimization algorithm for static total energy calculations was based on a residual minimization scheme-direct inversion in the iterative subspace (RMM- DIIS). Ground-state atomic geometries of surfaces and interfaces were optimized by minimizing the Hellman- Feyman forces using a combined blocked Davidson + RMM-DIIS algorithm, until the total forces on each ion was converged to 0.02 eV/ . The optimal choice of exchange-correlation (XC) functional was based on the comparison of predicted bulk properties with their experimental counterparts. The XC-functionals tested include local-density approximation (LDA), the generalized gradient approximation (GGA) with Perdew- Wang-91 functional (PW91) [32], and the Perdew- Burke-Ernzerhof (PBE) functional [33].

3 Results and discussion

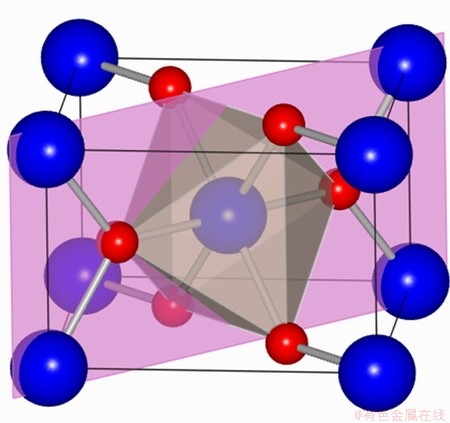
Fig. 1 Primitive tetragonal unit cell of SnO₂ (Red circles: O^2-; blue circles: Sn⁴⁺)

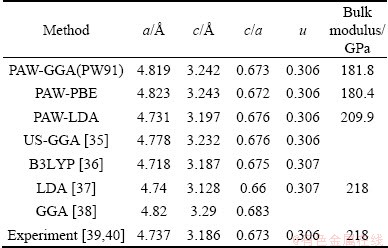
Table 1 Calculation of bulk SnO₂ in comparison with experiments and other calculations

3.1 Bulk properties

The validation of XC functionals can be performed by fitting the energy-volume data of crystalline materials to the Murnaghan’s equation of state [34] and comparing the predicted bulk properties with experiments. Taking SnO₂ as an example, it has a rutile (tetragonal) structure (space-group 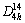, P4₂/mnm). Figure 1 presents the primitive cell of SnO₂. The atoms are located as O at 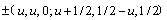and Sn at (0, 0, 0; 1/2, 1/2, 1/2), in units (a,a,c). The results of DFT bulk calculations using various exchange-correlation functionals are summarized in Table 1. It is seen that PAW-GGA and PAW-PBE predict quite similar results for lattice parameters and bulk modulus, which is expectable for that the two GGA-type functionals differ only by a simplified exchange enhancement factor. Both GGAs overestimate the experimental values by ~1.8 %. The overestimation resulted from the gradient corrections has an effect of isotropic pressure on the crystal, thus the predicted c/a ratio and the parameter of u could remain almost the same to experiment (0.673 and 0.306, respectively). PAW-LDA prediction has a much improved accuracy: the lattice parameters calculated by PAW-LDA (a=4.731 , c=3.197  and u=0.306) is in almost perfect agreement with the experimental data (a=4.737 , c=3.186 , u=0.306), within an error of only ~0.5%. The bulk modulus predicted by PAW-LDA also agrees well, within only a 3.7% of error. We thus have confidence to employ the PAW-LDA for SnO₂ in all subsequent calculations.

3.2 Surface energy, stoichiometry and stability

A stable oxide surface, that can be regarded as the end result of the dynamic balance of surface oxygen adsorption and desorption processes, must be modeled as in a thermal equilibrium at a certain temperature with an atmosphere containing a certain oxygen concentration. We employed the first-principle methods to explore a series of low-index surfaces with all possible ideal terminations, either stoichiometric or reduced or oxidized, under thermodynamic equilibrium with the ambient atmosphere.

Surface energy, as a measurement of surface stability, can be calculated as

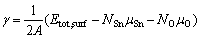
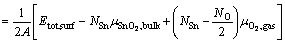  (1)

where μ_i is the elemental chemical potential, and N_i is the number of the corresponding atoms in the surface supercell. For a stoichiometric surface (N_O=2N_Sn), the surface energy must be independent of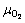, while for a nonstoichiometric or defective surface (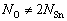), the surface energy becomes a linear function of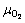. Assuming oxygen in the ambient as an ideal gas, one can express the oxygen chemical potential  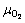as

 (2)

where 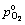 is taken to be 10⁵ Pa; k is the gas constant, 8.314 J/(K·mol); the superscript o represents the standard state of each species. Finally, the surface energy γ can be expressed as a function of T and  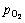as

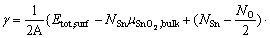
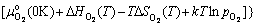 (3)

The temperature dependence of E_tot,surf and 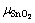 would essentially cancel out each other in computing the surface energy, thus can be approximated by DFT calculations at 0 K. The major contribution for the temperature dependence comes from the energetic terms of O₂. Among which, 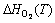and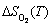can be referred to experimental values as tabulated in Ref. [41].

Table 2 summarizes the calculations of low-index stoichiometric surfaces in comparison with other earlier theoretical results. LDA predictions are 30%-60% higher than GGAs. The only full-potential calculation [42] yields surface energies that lie about half way between LDA and GGA results. No matter what exchange-correlation functional was used, the same order of stability was confirmed by DFT: (110)>(100)>(101)> (001). Due to that PAW-GGA or PBE tends to underestimate surface energy while PAW-LDA is opposite, we can predict the surface energies with error ranges as: g(110)≈1.19±0.19, g(100)≈1.31±0.24, g(101)≈1.61±0.19, g(001)≈(2.03±0.20) J/m². We note that, the (101) has a surface energy much higher than that of the (110) and (100). However, some experimental studies reported that SnO₂ (101) can be made stable under certain experimental conditions [43]. The unusual stability of the (101) occasionally observed in these experiments encourages us to further explore the dependence of non-stoichiometric surface stabilities under ambient conditions.

Table 2 Calculated surface energies of stoichiometric SnO₂ surfaces

According to Eq. (3), non-stoichiometric surface energy can no longer be a constant value but depend on T and 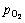. Figure 2 plots and compares the calculated low-index non-stoichiometric surface energies as functions of  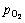at different temperatures. It is clear that at low temperatures, the stoichiometric termination of each surface yields the lowest surface energy over all the range of pressures up to 1×10⁵ Pa, while either the O- or the Sn-terminated counterpart always has a higher surface energy. With increasing temperature, the energies of the O-terminated surfaces further increase to even higher values, while those of the Sn-terminated surfaces can be reduced rapidly. Eventually, a termination transition from the stoichiometric to the Sn-rich may take place at ultra-high vacuum (UHV). For instance, at T= 1200 K, the stoichimetric-to-Sn-rich transition for the (101) surface occurs at ln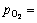~-17 (or 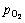=~10^-3 Pa). Below this pressure, the Sn-rich (101) would be the most stable facet. Our calculations can not only confirm, but also well explain those experimental observations that the (101) surface can be made stable under certain conditions. We also notice that the surface energies of (100)_Sn are very close to those of (101)_Sn at T>600 K. This suggests that both Sn-rich (100) and (101) might be expected to present as stable facets, at sufficiently low partial pressures and high temperatures. One should notice that we have only considered ideal terminations. In reality, such a termination transition is made possibly by a gradual and continuous loss of outermost layer oxygen atoms. But nevertheless, surface energy can employ Fig. 2 to estimate the critical pressures for termination transitions, to design or control the microstructure and property of an oxide surface.

3.3 Surface phase diagram

Figure 3 presents the equilibrium surface phase diagram constructed by replotting the transition pressure vs temperature data from our calculation in Fig. 2. This diagram contains only two regions dominated by the Sn-rich (101) and the stoichiometric (110) surface, respectively. The Sn-rich (101) is more favored under the conditions of high temperature and low oxygen partial pressures. It has been observed in Ref. [47] that simply increasing the oxygen partial pressure during the crystal growth at 1200 K could produce a branched hierarchical morphology of SnO₂ nano-wires. This very interesting experimental phenomenon can be well described by Fig. 3. At 1200 K, the reduced (101)_Sn and (100)_Sn have nearly equal low surface energies at low oxygen partial pressures, and thus both can preferentially grow as free stable facets; once the oxygen partial pressure is increased to cross the phase boundary (see from A to B in Fig. 3), the growth of (101)_Sn and (100)-Sn would cease automatically and the stoichiometric SnO₂ (110) starts to grow preferentially and steadily. Although the authors in Ref. [47] did not provide the exact values of oxygen partial pressures, the so-called controlled growth of branched hierarchical crystals with tunable morphology technique can be regarded as a successful application of our theoretically-constructed surface phase diagram (Fig. 3). The only direct experimental comparison that can be made is with the report in Ref. [48] (marked by C) where the {110} facets were found dominant in SnO₂ nanorods synthesized by thermal evaporation at 1200 K, and also, the relative intensity of the {110} facets indeed increased simultaneously with increasing oxygen partial pressures.

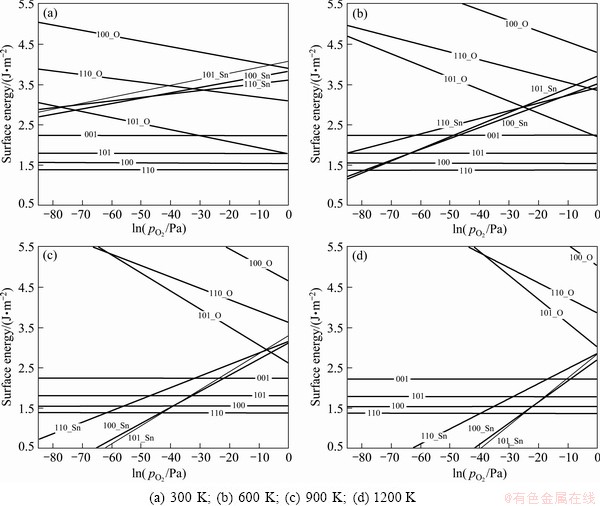
Fig. 2 Calculated surface energies of SnO₂ vs oxygen partial pressure at different temperatures

Fig. 3 Calculated surface phase diagram of SnO₂ (a), experimentally observed branched growth of SnO₂ nano-wires by adjusting ambient oxygen partial pressure at 1200 K (b) and a zoom-in view along growth direction of branches (c) (Length scales of (b) and (c) should be referred to Ref. [47])

3.4 Equilibrium crystal morphology

The calculated surface energies in Fig. 2 can be further utilized to predict the thermal equilibrium morphology of SnO₂ nano-particles, based on the Gibbs–Wulff theorem of equilibrium crystal shape (ECS) [49,50]. The Gibbs–Wulff theorem provides a simple mathematical construction that predicts the ECS of a single crystal or nano-particle by minimizing the total Gibbs free energy of a configuration of certain preferred crystal planes with low surface energies at a constant volume.

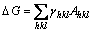                            (4)

The Wulff construction is performed based on a mathematical shape-energy relation as

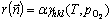                         (5)

where  represents the radius of the crystal shape in the normal direction to a particular crystal surface hkl; α is the proportionality constant. At a distance from the origin numerically equal to the surface energy,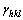, a normal plane is established as one potential facet of the ECS. Consequently, one returns to the origin and reiterates this process for all other crystallographic directions. In this way, the smallest volume enveloping the origin inside all these planes can be taken, in a geometrical sense, as the minimum-energy morphology for a particular crystal.

The equilibrium crystal shape of single crystal Ag can be constructed as shown in Fig. 4, based on our calculated surface energies of Ag. The faces of the spherical crystal Ag mostly consist of the most stable (111) planes, followed by (100) and then (110). Other higher-index Ag surfaces cannot possibly present due to the much higher surface energies. In contrast to pure metals, metal oxides would have an equilibrium crystal shape that changes at the ambient conditions, by following the environment dependence of surface energies. Figure 5 presents the predicted equilibrium crystal shape of SnO₂ at 1200 K, in a comparison with the experimentally observed morphologies of SnO₂ nanocrystals [51] and single crystals [42]. Different surface features with different electronic structures can thus exhibit different chemical reactivity and selectivity. Prediction of ECS is crucial for smart-designing of metal-oxide nanocrystals with desired morphologies and functions.

Fig. 4 Calculated surface energies of low-index Ag surfaces, and corresponding equilibrium crystal shapes of single crystal Ag

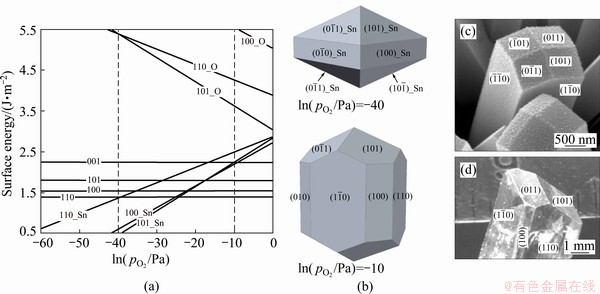
Fig. 5 Calculated surface energies of low-index SnO₂ surfaces at 1200 K (a), corresponding equilibrium crystal shapes of SnO₂ under two different oxygen partial pressures determined by Gibbs-Wulff theorem (b) and experimentally observed morphologies of SnO₂ nano-crystals (c) and single crystals (d) [42,51]

3.5 Interface structure

HRTEM can offer the unique ability to observe an interface directly in real space at the atomic scale. Microstructure observations by HRTEM combined with image simulations allow to deduce the interfacial orientation relationships, lattice mismatch, and even misfit dislocations in an intuitive way. However, conventional HRTEM assumes the independent atom model in which the atoms in the images are neutral, thus all kinds of interatomic interactions are neglected. This technique might be sufficient for structural and elemental identification within the specimen, but cannot provide enough chemical information, such as chemical interactions at the interface and the free energetics associated, that is demanded for an appropriate assessment of the stability and properties of an interface. To face such challenges, the conventional HRTEM was first employed to determine the basic orientation relation of the Ag-SnO₂ interface. The first-principles based strategy was then developed to provide many useful insights from an improved basic understanding of detailed interfacial structures, chemical bindings, and thermodynamics.

Fig. 6 Typical morphology of SnO₂ particles observed in internal oxidized Ag(Sn) composite alloy (a), HRTEM image of Ag-SnO₂ interface (b), and fast Fourier transform (FFT) pattern (c)

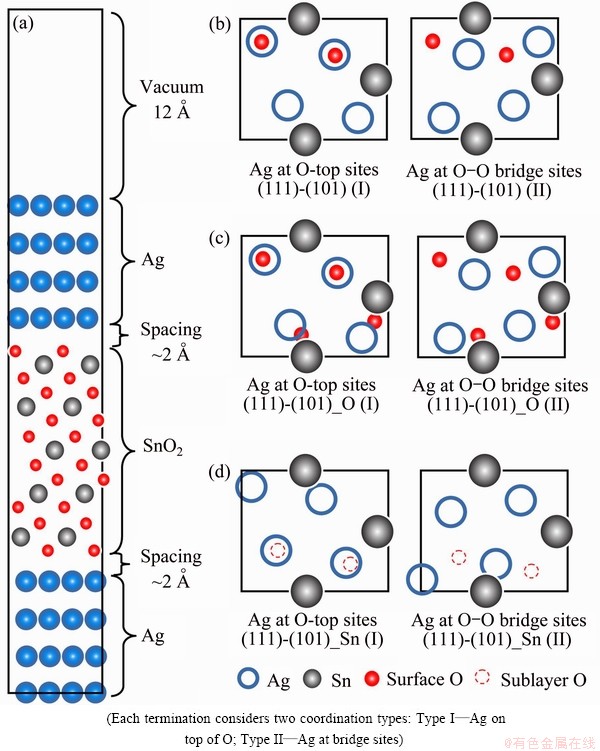
Fig. 7 Sandwich model for Ag(111)-SnO₂(101) stoichiometric interface, and top views of interface model with different terminations (a), stoichiometric (b), O-rich (c), and Sn-rich (d)

The metal-oxide interfaces formed by in-situ internal oxidation are smooth and clean, which is particularly preferable for microscopic characterization. Figure 6 shows the morphology of SnO₂ precipitates observed in Ag matrix and the high resolution transmission electron microscopy (Tecnai G² F20 S-TWIN) image of the interface along the beam axis of ＜110＞_Ag. A highly preferred growth orientation relation of  was observed for those fine-size oxide precipitates. Based on this information, an atomistic model for the Ag-SnO₂ interface can be constructed and shown in Fig. 7(a). This sandwich supercell is chosen to be the smallest repetitive unit in both x- and y-direction. Its inversion symmetry ensures a net-zero surface dipole moment across the vacuum (a thickness of at least 12 ). In this model, we chose the lowest strains to commensuration: the Ag lattice is compressed by only 3.8% to match the unstrained SnO₂ for the latter has much higher elastic moduli.

For such oxide interfaces, similarly as we have done for the surfaces, we need consider both stoichiometric and non-stoichiometric type terminations. For each termination, we further consider at least two different coordination types by translating metal relative to SnO₂, i.e., by placing Ag atoms on top of (Type I) or above the bridge sites (Type II) of the O atoms (as shown in Figs. 7(b)-(d)). The coordination type, along with interfacial terminations, indicates the chemical bonding nature and also the thermodynamics of the interface.

For all the considered structures, the calculations allow for full relaxation by varying atomic configurations in space until the total energy and the force on each atom are both minimized. The fully relaxed interface structures were presented and compared in Fig. 8. It is clearly seen that for the stoichiometric interfaces (the top panel), relaxation induced large lateral displacements of interfacial atoms, and eventually, the two initially different coordination structures (type I and II) relaxed to the same geometry. Similar relaxation consequence was observed for the O-terminated interfaces (the middle panel): the two coordination types relaxed to essentially the same geometry, they differ only by a mirror reflection but are geometrically and energetically identical. The resulted interfacial bonding is largely determined by strong covalent-ionic Ag-O bonds, and Ag atoms prefer to locate themselves at the hollow sites of neighboring O atoms (and vice versa). For the Sn-terminated interfaces (the bottom panel), interfacial atoms in both type structures only relaxed along the z-direction. The delocalized metallic bonds across the Sn-terminated interfaces well screen the influence of sub-layer oxygen atoms. Without being interfered by the surface oxygen atoms (as present in the stoichiometric case), Ag atoms preferentially sit at the bridge sites of Sn atoms.

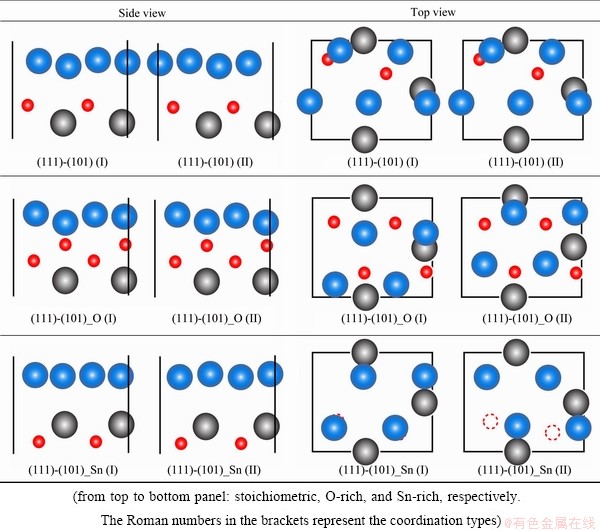
Fig. 8 Different interface terminations after relaxation

3.6 Adhesion strength and wettability

The adhesion strength and wettability of the interface can be evaluated by the reversible work of separation (W_sep) and work of adhesion (W_ed), respectively, from the first principles, as follows:

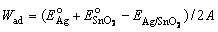          (6)

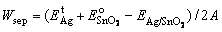          (7)

where 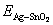is the total energy of the interface ensemble at its equilibrium state; 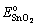and 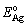 are the total energies of the unstrained SnO₂(101) and Ag(111) surface slab, respectively;  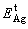is the total energy of the Ag(111) slab with the same strain as imposed in the interface ensemble, so that strain contributions to the energies of surface slabs can be dissociated from W_sep.

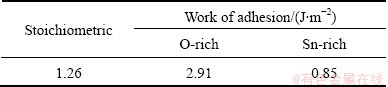
Table 3 lists the calculated work of adhesion for different interfaces with relevant stoichiometry, to show the impact of chemical binding details to wettability. At the O-terminated interface, the extra O atoms on the SnO₂ surface are unsaturated and are more active to form strong valence-ionic Ag—O bonds. The O-terminated interface thus has the highest W_ad of ~2.9 J/m², more than twice of the stoichiometric counterpart (~1.26 J/m²), where the surface O atoms are more saturated and the interfacial Ag—O bonds become more ionic and also weaker. The Sn-terminated interface is bonded mainly through metallic Ag—Sn bond. These metallic bonds are expected to be weak, for the valence electrons of surface Sn atoms have been mostly donated to sub-layer oxygen anions. Consequently, the Sn-terminated interface has the lowest value of W_ad, ~0.85 J/m², suggesting the lowest wettability of Sn-rich SnO₂ particles in Ag matrix. No direct experimental analyses have been yet done for characterizing the chemical binding at the Ag/SnO₂ interfaces, but similar results and tendencies have been seen in other previous studies for Cu/Al₂O₃ [52] and Ag/ZnO [53].

Table 3 Calculated work of adhesion for interfaces with different terminations

We further calculated the W_sep, at all possible cleavage planes, and determined the separation plane by finding the minimum W_sep. This can be regarded as an ab initio measurement of the fracture strength of Ag(111)/SnO₂(101). Basic work of separation results are summarized in Fig. 9. Corresponding to the highest value of W_ad (2.91 J/m²), the O-terminated interface also has the highest W_sep of 5.61 J/m² at the Ag-SnO₂ interface, much higher than those of the stoichiometric (1.48 J/m²) and the Sn-terminated interface (0.86 J/m²). The weakest interlayer binding always occurs right at the interface between the Ag and SnO₂ halves for both the stoichiometric and Sn-terminated interface, while for the strong O-terminated interface, the weakest interlayer binding was found between the first and the second layer of the Ag matrix (W_sep = ~2.80 J/m²), i.e., the fracture separation of this type interface tends to occur inside the Ag matrix, rather than exactly at the interface.

Fig. 9 Calculated work of separation of Ag(111)/SnO₂(101)

3.7 Interface energy and interface phase diagram

The interface energy can be expressed as a function of Sn activity, a_Sn, as

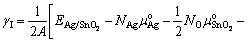
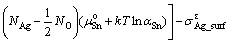    (8)

where 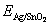is the total energy of the interface ensemble; N_i and μ_i (i = Ag, SnO₂, Sn) are respectively the number and chemical potential of each species i; the superscript ‘o’ refers to the pure bulk state of each species; the Sn activity, a_Sn, is the variable to link the thermodynamics of the Ag(Sn) composite alloy and the interface; A is the cross-sectional area of the interface; k is the Boltzmann constant; The term,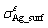, accounts for the surface energy of the extra, strained Ag(111) in the sandwich model.

The two elemental activities, a_Sn and a_O, are related as

            (9)

where 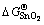is the standard formation energy of SnO₂. Assuming the thermodynamic equilibrium reaches on the alloy surface, i.e.,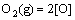, one can further relate a_Sn to 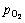as

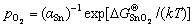            (10)

Thus, as an alternative to Eq. (8), interface energy can be also expressed as a function of .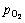

As suggested by Eqs. (8)-(10), the stoichiometric Ag/SnO₂ has a constant interface energy, independent of a_Sn and 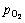. The O-terminated interface energy would increase with increasing  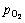(or decreasing a_Sn), while the Sn-terminated interface exhibits an opposite tendency. Thus, a non-stoichiometric, O-rich (or Sn-rich) interface could be possibly more thermodynamically favorable at sufficiently high (or low) oxygen partial pressures. The dependence of interface energy on elemental activity ( 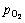or a_Sn) was calculated at 1023 K and is presented in Fig. 10. It is predicted that at 1023 K, the weakest Sn-terminated interface can be avoided by keeping 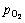>~e^-8.2 Pa, while the stoichiometric interface would dominate within the range from 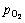= ~e^-8.2 Pa up to ~e¹ Pa. Above 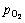= ~e¹ Pa, the most favored interface structure changes to the O-rich type, which as we predicted, has the highest adhesion strength.

We note that the ordering of the relative stabilities of interfacial terminations is actually defined by two threshold pressures for termination transitions, and the two threshold pressures vary with temperature. To manifest this, we further plotted the threshold points with respect to different temperatures (shown as solid curves) in Fig. 11, which can be seen as the equilibrium interface phase diagram of the Ag(111)/SnO₂(101). The upper and the lower limits of the feasible oxygen partial pressure range (represented as dash-dotted curves) can be further determined by avoiding the direct oxidation of Ag and guaranteeing the formation of SnO₂, in accordance with the reactions of 4Ag(s)+O₂(g)=2Ag₂O(S) and 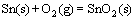, respectively. Environmental conditions defined in the region above the upper limit curve (the dash-dotted curve labeled as Ag₂O) would favor undesired external oxidation, i.e., the direct oxidation of the Ag matrix, whereas those defined in the region below the lower limit curve (the dash-dotted curve labeled as SnO₂ curve) suggest no oxidation to possibly occur. Only in the region between the two limit curves can the internal oxidation be thermodynamically feasible. In most industrial practices, internal oxidation of binary Ag-alloys is performed within the temperature range of 873-1073 K [54]. This practical temperature range is also marked by two vertical dotted lines in Fig. 11.

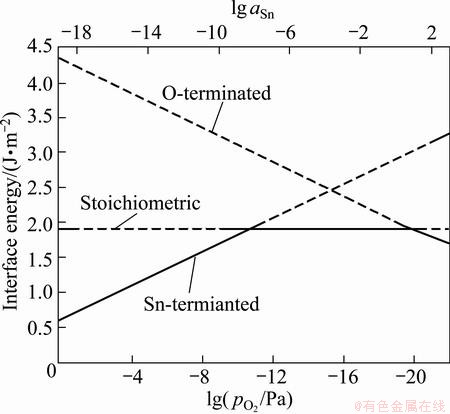
Fig. 10 Interface energy of Ag/SnO₂ with different terminations at 1023 K as function of a_Sn and

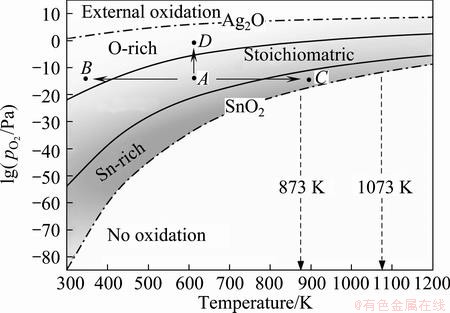
Fig. 11 Calculated equilibrium interface phase diagram of Ag/SnO₂

The interface phase diagram (Fig. 11) is extremely useful to explore optimal processing parameters, to achieve appropriate interfacial microstructures with desired properties. To illustrate the utility of the diagram, we now focus on the formation of strong O-rich interfaces in Ag(Sn). Given a practical oxygen partial pressure, say =e^-15 Pa, to favor the formation of O-rich interfaces, a relatively lower temperature (from A to B) seems reasonable but is not at all practical due to the extremely low atomic diffusivity at such a low temperature. Increasing temperature (from A to C) can certainly facilitate the diffusion of atoms and thus the oxidation process, but the formed oxides would likely be Sn-rich, with the weakest interfaces of the Ag matrix. Instead of changing temperature, a more effective solution is to simply adjust the external oxygen partial pressure from A to D, i.e., by increasing it across the upper solid curve (namely the stoichiometric-to-O-rich termination transition curve).

4 Conclusions

Taking SnO₂ as an example, we demonstrated a systematic theoretical strategy for studying metal oxide surfaces and interfaces using defect thermodynamic modeling and first principles energetics calculations. We first modeled and calculated the formation energies of all non-stiochiometric low-index SnO₂ surfaces as a function of the ambient temperature and oxygen partial pressure. With the results, we can construct the surface phase diagram to predict the equilibrium surface structure at any given T and 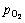. The Gibbs–Wulff construction was further performed to predict the environment- dependent equilibrium morphologies of SnO₂ nano- particles. As for the internally oxidized SnO₂ interfaces with Ag matrix, the HRTEM analyses were first performed to determine the basic orientation relation, and based on which, various atomistic models for possible interface structures were proposed with considering different stoichiometry/termination and coordination types. The associated free energies and properties (adhesion strength, wettability, and relative stabilities) were then evaluated from ab initio calculations at any given T and 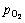. The equilibrium interface phase diagram was eventually constructed, to enable us elucidate the environment-microstructure- property relations of the interfaces during the in-situ fabrication of Ag-SnO₂ composites. Understanding the thermodynamics of internal interfaces and its relation with fabrication processing parameters is a crucial step towards the fundamental understanding the overall mechanical properties of composite materials. Our eventual goal is to achieve a full knowledge-based design freedom, to realize the capability of engineering the microstructures for desired properties by smartly choosing the processing parameters.

Acknowledgments

The computational resources at the High Performance Computing Center of Central South University are gratefully acknowledged. One of us (Yong JIANG) would like to thank the Chinese Ministry of Education’s Supportive Program for New Century Excellent Talents in Universities.

References

[1] FORTUNATO E, GINLEY D, HOSONO H, PAINE D C. Transparent conducting oxides for photovoltaics [J]. Materials Research Society Bulletin, 2007, 32(3): 242-247.

[2] ROBERTSON J. High dielectric constant gate oxides for metal oxide Si transistors [J]. Reports on Progress in Physics, 2006, 69(2): 327-396.

[3] MA J, HU J, LI Z, NAN C W. Recent progress in multiferroic magnetoelectric composites: From bulk to thin films [J]. Advanced Materials, 2011, 23(9): 1062-1087.

[4] LI Y J, KWON Y W, JONES M, HEO Y W, ZHOU J, LUO S C, HOLLOWAY P H, DOUGLAS E, NORTON D P, PARK Z, LI S. Progress in semiconducting oxide-based thin-film transistors for displays [J]. Semiconductor Science and Technology, 2005, 20(8): 720-725.

[5] LI Z, FREDIN L A, TEWARI P, DIBENEDETTO S A, LANAGAN M T, RATNER M A, MARKS T J. In-situ catalytic encapsulation of core-shell nanoparticles having variable shell thickness: Dielectric and energy storage properties of high-permittivity metal oxide nanocomposites [J]. Chemistry of Materials, 2010, 22(18): 5154-5164.

[6] JIANG Y, ADAMS J B, SUN D. Benzotriazole adsorption on Cu₂O(111) surfaces: A first-principles study [J]. The Journal of Physical Chemistry B, 2004, 108(34): 12851-12857.

[7] MEYER J, HAMWI S,  M, KOWALSKY W, RIEDL T, KAHN A. Transition metal oxides for organic electronics: Energetics, device physics and applications [J]. Advanced Materials, DOI: 10.1002/adma.201201630.

[8] JIANG Y, ADAMS J B, VAN SCHILFGAARDE M, SHARMA R, CROZIER P A. Theoretical study of environmental dependence of oxygen vacancy formation in CeO₂ [J]. Applied Physics Letters, 2005, 87(14): 141917.

[9] LAN G Q, JIANG Y, YI D Q, LIU S J. Theoretical prediction of impurity effects on the internally oxidized metal/oxide interface: The case study of S on Cu/Al₂O₃ [J]. Physical Chemistry Chemical Physics, 2012, 14(31): 11178-11184.

[10] JIANG Y, SMITH J R, EVANS A G. First principles assessment of metal/oxide interface adhesion [J]. Applied Physics Letters, 2008, 92(14): 141918.

[11] MA H, YIP H L, HUANG F, JEN A K Y. Interface engineering for organic electronics [J]. Advanced Functional Materials, 2010, 20(9): 1371-1388.

[12] JIANG Y, ADAMS J B, van SCHILFGAARDE M. Density- functional calculation of CeO₂ surfaces and prediction of effects of oxygen partial pressure and temperature on stabilities [J]. Journal of Chemical Physics, 2005, 123(6): 064701.

[13] GORDON R G, PROSCIA J, ELLIS J R F B, DELAHOY A E. Textured tin oxide films produced by atmospheric pressure chemical vapor deposition from tetramethyltin and their usefulness in producing light trapping in thin film amorphous silicon solar cells [J]. Solar Energy Materials, 1989, 18(5): 263-281.

[14] THANGARAJU B. Structural and electrical studies on highly conducting spray deposited fluorine and antimony doped SnO₂ thin films from SnCl₂ precursor [J]. Thin Solid Films, 2002, 402(1-2): 71-8.

[15] LEE G G, KANG S J L. Formation of large pores and their effect on electrical properties of SnO₂ gas sensors [J]. Sensors and Actuators B: Chemical, 2005, 107(1): 392-396.

[16] BATZILL M, DIEBOLD U. The surface and materials science of tin oxide [J]. Progress in Surface Science, 2005, 79(2-4): 47-154.

[17] CHEN Y C, CHEN J M, HUANG Y H, LEE Y R, SHIH H C. Size effect of tin oxide nanoparticles on high capacity lithium battery anode materials [J]. Surface and Coatings Technology, 2007, 202(4-7): 1313-1318.

[18] TALIJAN N M, Electrical contact materials based on silver [J]. Materijala, 2011, 52(3): 173-180.

[19] NILSSON O, HAUNER F, JEANNOT D. Replacement of Ag/CdO by Ag/SnO₂ in DC contactors [C]// 2004 Proceedings of the 50th IEEE HOLM Conference on Electrical Contacts and the 22nd International Conference on Electrical Contacts, Seattle, Waskington, USA: IEEE, 2004:70-74.

[20] RIEDER W, WEICHSLER V. Make erosion mechanism of Ag/CdO and Ag/SnO₂ contacts [J]. IEEE Transactions on Components, Hybrids, and Manufacturing Technology, 1992, 15(3): 332-338.

[21] GENGENBACH B, MAYER U, MICHAL R, SAEGER K. Investigation on the switching behavior of Ag-SnO₂ materials in commercial contactors [J]. IEEE Transactions on Components, Hybrids, and Manufacturing Technology, 1985, 8(1): 58-63.

[22] LUNGU M, GAVRILIU S, CANTA T, LUCACI M, ENESCU E. Ag-SnO₂ sintered electrical contacts with ultrafine and uniformly dispersed microstructure [J]. Journal of Optoelectronics and Advanced Materials, 2006, 8(2): 576-581.

[23] KRA ' TZSCHMAR A, HERBST R, MUTZEL T, NIEDERREUTHER R, BRAUMANN P. Basic investigations on the behavior of advanced Ag-SnO₂ materials for contactor applications [C]//Proceedings of the 56th IEEE HOLM Conference on Electrical Contacts. Charleston, South Carolina, USA: IEEE, 2010: 1-7.

[24] XU C, JIANG Y, YI D, SUN S, YU Z. Environment-dependent surface structures and stabilities of SnO₂ from the first principles [J]. Journal of Applied Physics, 2012, 111(6): 063504.

[25] ZHANG W, SMITH J R, WANG X G, EVANS A G. Influence of sulfur on the adhesion of the nickel/alumina interface [J]. Physical Review B, 2003, 67(24): 245414.

[26] SMITH J R, JIANG Y, EVANS A G. Adhesion of the Ni(Al)/Al₂O₃ interface: A first-principle assessment [J]. International Journal of Materials Research, 2007, 98: 1214-1221.

[27] HOHENBERG P, KOHN W. Inhomogeneous electron gas [J]. Physical Review B, 1964, 136(3B): 864-871.

[28] KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects [J]. Physical Review A, 1965, 140: 1133-1138.

[29] KRESSE G, MARSMAN M, FURTHMULLER J. VASP Guide [EB/OL]. http://cms.mpi.univie.ac.at/vasp, 2012.

[30] KRESSE G, JOUBERT J. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758-1775.

[31] MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 13(12): 5188-5192.

[32] PERDEW J P, CHEVARY J A, VOSKO S H, JACKSON K A, PEDERSON M R, SINGH D J, FIOLHAIS C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46(11): 6671-6687.

[33] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865-3868.

[34] MURNAGHAN F D. The compressibility of media under extreme pressures [J]. Proceedings of the National Academy of Sciences, 1944, 30(9): 244-247.

[35] OVIEDO J, GILLAN M J. Energetics and structure of stoichiometric SnO₂ surfaces studied by first-principles calculations [J]. Surface Science, 2000, 463(2): 93-101.

[36] SENSATO F R, CUSTODIO R, CALATAYUD M, BELTR’AN A, ANDR’ES J, SAMBRANO J R, LONGO E. Periodic study on the structural and electronic properties of bulk, oxidized and reduced SnO₂(110) surfaces and the interaction with O₂ [J]. Surface Science, 2002, 511(1-3): 408-420.

[37] MEYER M, ONIDA G, PALUMMO M, REINING L. ab initio pseudopotential calculation of the equilibrium structure of tin monoxide [J]. Physical Review B, 2001, 64(4): 51191-51199.

[38] GOLOVANOV V, VIITALA M, KORTELAINEN T, CRAMARIUC O, RANTALA T T. Stability of siloxane couplers on pure and fluorine doped SnO₂ (110) surface: A first principles study [J]. Surface Science, 2010, 604(19-20): 1784-1790.

[39] BOLZAN A A, FONG C, KENNEDY B J, HOWARD C J. Structural studies of rutile-type metal dioxides [J]. Acta Crystallographica Section B: Structure Science, 1997, 53(3): 373-380.

[40] POSTNIKOV A V, ENTEL P, P. SnO₂: bulk and surface simulations by an ab-initio numerical local orbitals method [J]. Phase Transitions, 2002, 75(1-2): 143-147.

[41] STULL D R, PROPHET H. JANAF thermochemical tables [S]. 2nd ed. Washington, DC: U.S. National Bureau of Standards, 1971.

[42] BATZILL M, KATSIEV K, BURST J M, DIEBOLD U, CHAKA A M, DELLEY B. Gas-phase-dependent properties of SnO₂ (110), (100), and (101) single-crystal surfaces: Structure, composition, and electronic properties [J]. Physical Review B, 2005, 72(16): 165414.

[43] DOMINGUEZ J E, FU L, PAN X Q. Epitaxial nanocrystalline tin dioxide thin films grown on (0001) sapphire by femtosecond pulsed laser deposition [J]. Applied Physics Letter, 2001, 79(5): 614-616.

[44] GONIAKOWSKI J, HOLENDER J M, KANTOROVICH L N, GILLAN M J, WHITE J A. Influence of gradient corrections on the bulk and surface properties of TiO₂ and SnO₂ [J]. Physical Review B, 1996, 53(3): 957-960.

[45] MANASSIDIS I, GONIAKOWSKI J, KANTOROVICH L N, GILLAN M J. The structure of the stoichiometric and reduced SnO₂(110) surface [J]. Surface Science, 1995, 339(3): 258-271.

[46] BERGERMAYERA W, TANAKA I. Reduced SnO₂ surfaces by first-principles calculations [J]. Applied Physics Letter, 2004, 84(6): 909-911.

[47] LIU J, CHEN X L, WANG W J, SONG B, HUANG Q S. Secondary facet-selective nucleation and growth: Highly oriented straight SnO₂ nanowire arrays on primary microrods [J]. Crystal Growth & Design, 2009, 9(4): 1757-1761.

[48] KIM H W, LEE J W, SHIM S H, LEE C. Controlled growth of SnO₂ nanorods by thermal evaporation of Sn powders [J]. Journal of the Korean Physical Society, 2007, 51(1): 198-203.

[49] WULFF G. Zur frage der geschwindigkeit des wachstums und der der [J]. Kristallogr Z, 1901, 34: 449-530.

[50] HERRING C. Some theorems on the free energies of crystal surfaces [J]. Physics Review, 1951, 82: 87-93.

[51] LIU Y, DONG J, LIU M. Well-aligned “nano-box-beams”of SnO₂ [J]. Advanced Materials, 2004, 16(4): 353-356.

[52] HASHIBON A, M. Structure at abrupt copper-alumina interfaces: An ab initio study [J]. Acta Materialia, 2005, 53(20): 5323-5332.

[53] PHILLIPS C L, BRISTOWE P D. First principles study of the adhesion asymmetry of a metal/oxide interface [J]. Journal of Materials Science, 2008, 43(11): 3960-3968.

[54] TOSHIYUKI O, KICHKON R, KOJI H, TORU K, NOBUYUKI Y, AKIHIKO I. Production of fine wire for Ag-oxide electrical contact: Japan, 9111364 [P]. 1997.

金属氧化物表面与界面的第一性原理热力学: 一个研究实例

江 勇^1,2, 许灿辉^1,2, 蓝国强^1,2

1. 中南大学 材料科学与工程学院，长沙 410083；

2. 中南大学 有色金属材料科学与工程教育部重点实验室，长沙 410083

摘  要：通过第一性原理计算研究，能够揭示和阐明材料相关表面与界面热力学性质，这是通向纳米和界面材料设计自由的重要一步，即以理想性能为目标，科学设计制备工艺参数，针对性地调控材料微观结构。以SnO₂纳米颗粒表面和原位内氧化制备获得的Ag-SnO₂界面计算研究为例，系统介绍这一计算研究策略。基于缺陷热力学模型，构建不同环境温度和氧分压条件下所对应的热力学平衡状态的表面和界面结构模型，计算评估其相应性能。通过一系列的第一性原理能量学计算，进一步构建出平衡状态的表面与界面相图。这些相图能够充分描述制备和服役过程中，工况对材料表面和界面微观结构和相应性能的影响和作用关系。介绍和讨论如何应用这些相图理解和科学设计相应材料的制备工艺。

关键词：金属氧化物；表面相图；界面相图；平衡晶体形状；第一性原理；热力学

(Edited by Xiang-qun LI)

Foundation item: Project (51171211) supported by the National Natural Science Foundation of China; Project (NCET-10-0837) supported by the Chinese Ministry of Education’s Supportive Program for New Century Excellent Talents in Universities; Project (2006BAE03B03) supported by the Chinese National Science and Technology Supportive Program

Corresponding author: Yong JIANG; Tel: +86-731-88830263; Fax: +86-731-88836320; E-mail: yjiang@csu.edu.cn

DOI: 10.1016/S1003-6326(13)62445-0