Travel modal choice analysis for traffic corridors based on decision-theoretic approaches
来源期刊:中南大学学报(英文版)2016年第11期
论文作者:张毅 郭伟 尤佳轩 胡坚明 裴欣
文章页码:3028 - 3039
Key words:modal choice analysis; traffic corridor modelling; decision field theory
Abstract: The rapid development of multimodal transportation system prompts travellers to choose multiple transportation modes, such as private vehicles or taxi, transit (subways or buses), or park-and-ride combinations for urban trips. Traffic corridor is a major scenario that supports travellers to commute from suburban residential areas to central working areas. Studying their modal choice behaviour is receiving more and more interests. On one hand, it will guide the travellers to rationally choose their most economic and beneficial mode for urban trips. On the other hand, it will help traffic operators to make more appropriate policies to enhance the share of public transit in order to alleviate the traffic congestion and produce more economic and social benefits. To analyze the travel modal choice, a generalized cost model for three typical modes is first established to evaluate each different travel alternative. Then, random utility theory (RUT) and decision field theory (DFT) are introduced to describe the decision-making process how travellers make their mode choices. Further, some important factors that may influence the modal choice behaviour are discussed as well. To test the feasibility of the proposed model, a field test in Beijing was conducted to collect the real-time data and estimate the model parameters. The improvements in the test results and analysis show new advances in the development of travel mode choice on multimodal transportation networks.
J. Cent. South Univ. (2016) 23: 3028-3039
DOI: 10.1007/s11771-016-3366-8
GUO Wei(郭伟)1, ZHANG Yi(张毅)1, 2, YOU Jia-xuan(尤佳轩)1, HU Jian-ming(胡坚明)1, 2, PEI Xin(裴欣)1, 2
1. Department of Automation, Tsinghua National Laboratory for Information Science and Technology (TNList), Tsinghua University, Beijing 100084, China;
2. Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Nanjing 210096, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The rapid development of multimodal transportation system prompts travellers to choose multiple transportation modes, such as private vehicles or taxi, transit (subways or buses), or park-and-ride combinations for urban trips. Traffic corridor is a major scenario that supports travellers to commute from suburban residential areas to central working areas. Studying their modal choice behaviour is receiving more and more interests. On one hand, it will guide the travellers to rationally choose their most economic and beneficial mode for urban trips. On the other hand, it will help traffic operators to make more appropriate policies to enhance the share of public transit in order to alleviate the traffic congestion and produce more economic and social benefits. To analyze the travel modal choice, a generalized cost model for three typical modes is first established to evaluate each different travel alternative. Then, random utility theory (RUT) and decision field theory (DFT) are introduced to describe the decision-making process how travellers make their mode choices. Further, some important factors that may influence the modal choice behaviour are discussed as well. To test the feasibility of the proposed model, a field test in Beijing was conducted to collect the real-time data and estimate the model parameters. The improvements in the test results and analysis show new advances in the development of travel mode choice on multimodal transportation networks.
Key words: modal choice analysis; traffic corridor modelling; decision field theory
1 Introduction
Due to the rapid development of metropolis in China, excessive increase of vehicles, heavy traffic congestion, traffic safety and environmental pollution are becoming more and more serious. To alleviate the above problems, public transit has been encouraged to facilitate people’s travels. Multimodal trips, consisting of at least of two or more travel modes, are becoming more and more popular. Multimodal transportation systems are expected to become more important in the future due to their contributions to the sustainable urban transportation and traffic administrators are committed to increasing the share of multimodal trips in order to guarantee a high level of urban mobility [1]. The study on travel mode choice behaviour modelling and analysis in multimodal transportation system attracts more and more concerns, because travel mode choice of urban trips is significant determinants of urban travel demand [2].
Several measures had been developed in this last two decades to enhance the service level of multimodal transport network. Various studies could be roughly categorized into two kinds.
The first kind of studies focused on the dynamics of multimodal transport networks. Several models were proposed to characterize the traffic flow assignment in multimodal networks [3-4]. By modelling the features of network nodes or links, these new models helped researchers to obtain the optimal equilibrium state of the multimodal network [5]. The achievements of such kind of studies contribute to increasing the efficiency of transport network.
The second kind studies focused on modelling the traveller’s choice behaviour. Utility models and discrete choice models were involved to evaluate the different mode options [6-7]. Their work effectively analyzed and predicted the traffic sharing rates of different travel modes in multimodal networks and it must be beneficial to alleviate the traffic congestion problem.The approach discussed in this work belongs to the second kind. We attempt to model the travel cost of different travel modes based on real-time data and formulate the traveller’s decision-making process. To characterize the travel mode choice issues, there are three problems that needs to be addressed.
The first one is how to select the appropriate studying scenario. Home-work commuting is considered the most important daily travels of human beings. So, the analysis on mode choice behaviour of home-work commuting is very significant. In many Chinese metropolis, traffic corridors involving parallel roadways and transit lines are the main facilities to serve the commuters’ travel demand from suburban residential areas to central business district (CBD) [8]. In this work, we select a representative traffic commuting corridor in Beijing, which is equipped with an expressway (Jingtong Expressway) and a transit line (Beijing Subway Line 1). Graph theoretic model is applied to formulate the corridor scenario.
The second one is how to evaluate the options of different travel modes. Previous studies proposed the different models of multimodal transport network to characterize people’s travelling behaviours [9-10], which includes logit-based choice models [11], multinomial probit models [12], dynamic assignment models [13] and so on. In our case, we adopt quantitative models to formulate the real-time generalized travel cost of different modes. It should be noticed that the choices of transportation costs combinations are based on factors other than just transportation costs, which are related to transit time, distance, money, intermodal transfers [14]. A field test was conducted to collect real-time data and estimate the parameters of proposed models.
The third one is how to formulate the decision- making process when faced with different mode alternatives. In this work, two typical decision-theoretic approaches were introduced to characterize the complex decision-making process. One is the static random utility theory (RUT) [15-16] and the other is the dynamic decision field theory (DFT)[17]. RUT is a classical discrete choice model that has the advantage of simple mathematical descriptions and easy computational process. Whereas, DFT is an advanced, stochastic and dynamic decision models involving the effects of the factors of deliberation time, attention on decision behaviour. Besides, several successful applications of RUT and DFT in other fields enlightened us to adopt the decision theories to travel modals choice. The comparison of RUT and DFT on travel modal choice would also be made as well.
2 Mathematical formulation of travel mode choice model
In this section, a typical traffic corridor scenario in Beijing is selected and formulated into a graph network. And then, a generalized travel cost model is proposed. At last, RUT and DFT are introduced to characterize the choice decision-making process.
2.1 Scenario representation
In a modern metropolis, there usually are several main corridors for commuting from suburban areas to the central business district (CBD). The main corridors contain several major transportation modes and serve for commuters. Figure 1 illustrates a representative traffic commuting corridor in Beijing, which serves residents who commute from suburban Tongzhou District to Guomao CBD.
The traffic corridor contains a transit line, called Beijing Transit Line 1, and an expressway, called Jingtong Expressway. Thus, the multimodal transportation system supports commuters to choose three types of travel modes: private vehicles (self-driving or taxi), public transit (subway or bus) and park-and-ride (P&R). We use a graph model to formulate the real scenario as a network with an expressway and a subway line (see Fig. 2).
Suppose that the corridor network includes N subway links and the expressway is then divided into N roadway links as well. In this work, we focus on the modal choice among the three following travel modes: subway mode for transit, expressway mode for private vehicles and P&R mode for park-and-ride combination. As illustrated in Fig. 2, there are N+1 subway stations and N+1 parking lots nearby, which divide the corridor network into N consecutive segments. For the subway mode, the subway stations are denoted as Si, and the subway links between Si and Si-1 are denoted as si,i=0, …, N. For the expressway mode, the parking lots are denoted as Ei, and the expressway links between Ei and Ei-1 are denoted as ei, i=0, …, N. P&R mode is actually a combination of expressway mode and subway mode. We assume that commuters of P&R mode only transfers from expressway mode to the subway mode. The corresponding transfer links are denoted as pi connecting the pairs (Ei, Si), i=1, …, N-1. At last, the entrance links from the origin Oi to Ei and Si are denoted as  and
and  , i=1, …, N; and the exit links from E0 and S0 are denoted as xe and xs, respectively.
, i=1, …, N; and the exit links from E0 and S0 are denoted as xe and xs, respectively.
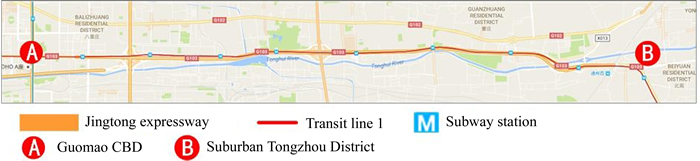
Fig. 1 Scenario of a traffic commuting corridor in Beijing
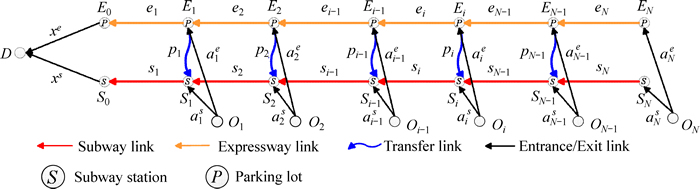
Fig. 2 Formulated network of traffic corridors in Beijing
In addition, it is assumed that the distance between the pairs (Ei, Ei-1) is equivalent to that between the pairs (Si, Si-1), which is denoted as di, i=1, …, N. The distance of entrance/exit links or transfer links is ignored, because commuters probably go on foot within these links. Thus, the total distance of commuting corridor can be calculated as
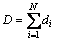 (1)
(1)
2.2 Mathematical formulation of generalized travel cost
Researchers have proposed several quantitative models for urban transportation system to evaluate the transportation serviceability [18-19]. It brings us much inspirations in travel cost modelling. Thus, we construct our models based on their innovative work.
It should be clarified that under different circumstances, the composition of travel cost varies significantly in different travel modes [20]. In this work, we evaluate the general travel cost by involving the travel time, travel expense and travel comfort for expressway, subway and P&R modes accordingly.
For presentation simplicity, the symbols and notations are enumerated in Table 1.
1) Generalized travel cost of subway mode
The underground transit line is obviously escaping from the traffic congestion on road. Thus, the total travel time of subway mode 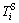 from Si to CBD only involves the entrance time
from Si to CBD only involves the entrance time 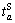 , the exit time
, the exit time 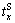 and the travel time. It can be written as
and the travel time. It can be written as
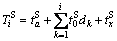 (2)
(2)
The travel expense of subway  contains two main components: the benchmark price m0 and distance- based additional price
contains two main components: the benchmark price m0 and distance- based additional price 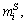 which can be written as
which can be written as
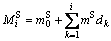 (3)
(3)
Travel comfort in subway system relates with many kinds of factors [21]. Actually, most of them are influenced by the density of in-carriage passengers. So, we use a typical comfort measure function gS(·), which is controlled by the passenger flow, to describe traveller’s comfort. Accordingly, the travel comfort can be written as
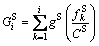 (4)
(4)
where gS(x)=ω(1-e-x/θ); ω and θ are scaling and shape coefficients of comfort measure function, respectively. Giving the function gS(·) for the comfort measurement, it is reasonable to assume that 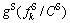 increases with the increment of
increases with the increment of  and if
and if

Summarizing the travel time, travel expense and travel comfort, the generalized travel cost 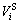 from Si to CBD can be written as
from Si to CBD can be written as
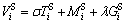 (5)
(5)
where σ, λ are transform coefficients of  respectively. They represents the value of time (VOT) and value of comfort (VOC), respectively.
respectively. They represents the value of time (VOT) and value of comfort (VOC), respectively.
2) Generalized travel cost of expressway mode
The travel time of expressway mode might be affected by traffic congestion. We use the well-known US Bureau of Public Roads function (BPR function) to calculate the travel time [22]. According to BPR function, the congestion travel time 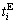 involves the free flow travel time
involves the free flow travel time 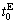 and the traffic flow
and the traffic flow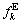 , which can be written as
, which can be written as
Table 1 Nomenclature list of generalized travel cost models

 (6)
(6)
where α, β are the coefficients of BPR function.
Then, we should add the entrance  and exit time
and exit time  , the total travel time
, the total travel time  from Ei to CBD can be written as
from Ei to CBD can be written as
 (7)
(7)
The travel expense includes three components: the distance-based expressway toll 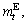 fuel charge
fuel charge 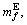 the parking fees
the parking fees 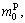 which can be formulated as
which can be formulated as
 (8)
(8)
It should be clarified that we assume that all the travellers will park fixed time (i.e. 8 h) in the parking lot. So, the parking fees can be calculated correspondingly. Since taking vehicle is much more comfortable because of its escape from in-car crowding, we assume that the travel comfort cost in vehicle  So, the generalized travel cost
So, the generalized travel cost  from Ei to CBD can be written as
from Ei to CBD can be written as
 (9)
(9)
3) Generalized travel cost of P&R mode
In P&R mode, the commuters may drive from origin Oi to parking lot Ei and transfer to subway station Si and then take a transit line to CBD.
So, the travel time of P&R mode contains five components: entrance time  travel time in vehicles
travel time in vehicles  transfer time
transfer time  travel time in metros
travel time in metros  exit time
exit time 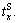 It can be written as
It can be written as
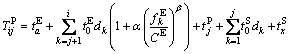 (10)
(10)
For travel expense, it can be determined by summing up above-mentioned expense components as
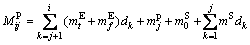 (11)
(11)
Regarding to travel comfort cost of P&R mode, it actually involves the travel comfort of subway mode since the cost of expressway mode is assigned to zero. It can be formulated as
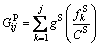 (12)
(12)
Similar to the former two modes, the generalized travel cost of P&R mode  from Ei to Sj and then to CBD can be formulated as
from Ei to Sj and then to CBD can be formulated as
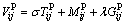 (13)
(13)
2.3 Mathematical formulation of decision-making process
To explore the modal choice behaviour, we use the choosing probability of one certain travel mode to characterize traveller’s choice. It is assumed here that the traveller’s may randomly choose their traffic modes to minimizing their commuting travel cost. We introduce two classical decision theories, random utility theory (RUT) and decision field theory (DFT).
1) Choice modeling based on RUT
Logit model is adopted to characterize the choice behaviour. It has the advantage of fast computing speed, simplified mathematical expression and extensive applicability. RUT declares that decision makers make a choice between uncertainty and prospects by comparing the utility values of different options. The essential hypothesis of RUT is that we assume all the decision makers are characterized with absolute rationality.
The stochastic generalized travel cost Uη of travel mode η can be written as
 (14)
(14)
where Vη is the actual observations of generalized travel cost for mode η, and εη is the stochastic error term for unobservable factors. So, the travellers may minimize their generalized travel cost by choosing a traffic mode with probability:
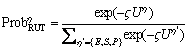 (15)
(15)
where  is a scaling parameter.
is a scaling parameter.
2) Choice modeling based on DFT
Decision field theory is a dynamic and cognitive method to model the decision-making process for human-beings based on psychological principles [23]. Compared to the above classical static decision theory, DFT concentrates on the psychological deliberation process and the effects of deliberation time point. It also reflects the mechanism how decision makers generate their preference. DFT describes the decision making behaviour from a psychological point of view. Different from those traditional decision theories, DFT is a stochastic and dynamic approach that uncovers the effect of cognitive ability, deliberation time and other psychological factors.
Several researchers [24-25] utilized a three-layer network to illustrate how DFT works (see Fig. 3). The first layer of the network computes the travel cost of different mode options, which has been formulated in Subsection 2.2. We extend those static generalized cost models to dynamic ones by adding a temporal parameter τ, which denotes the deliberation time of decision-makers.
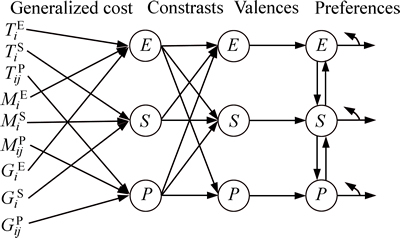
Fig. 3 Three-layer network model of DFT
So, the dynamic generalized travel cost of travel mode η can be written as
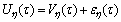 (16)
(16)
The second layer of the network computes the differential valences, which denotes the superiority and inferiority of each mode choice at deliberation time τ, described as
 (17)
(17)
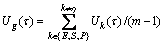 (18)
(18)
where vη(τ) indicates the valence for traffic mode η; Ug(τ) represents the other (m-1) mode options and m is the number of traffic modes. In our case, m=3.
The third layer generates the travel preference through a competitive recursive algorithm. The travel preference at a particular time point is integrated by the preference value at previous time points and the input valences. According to Ref. [23], preference state can be formulated by a linear dynamic system as follows:
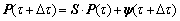 (19)
(19)
where P(τ) is the preference vector for all mode options at deliberation time τ. Each component of P(τ) actually indicates the choosing probability of different modes.ψ(τ) is the differential valence vectors and S is the feedback matrix.
Further, Eq. (19) can be expanded as
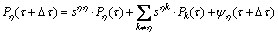 (20)
(20)
where Pη(τ) denotes the preference for mode option η at time τ; sηη is the self-feedback coefficient positive value and sηk is the negative mutual feedback coefficient value.
BUSEMEYER et al [26-27] gave a detailed explanation for the reference value of sηη. sηη=0 suggests no impact of previous valences over time; 0
 (21)
(21)
 (22)
(22)
where d can be calculated as
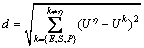 (23)
(23)
In our case, we choose the first calculating methods to determine the mutual feedback coefficient sηk.
When implementing DFT model, a stopping criterion needs to be set to terminate the recursive algorithm. ROE et al [25] proposed two kinds of stopping criteria respectively regarding deliberation time and preference value. The first one is that decision maker will choose his/her option with the maximum preference state within a fixed deliberation time period. The second one is that, without a time limit, the deliberation process will not stop until any one of the preference states exceeds a threshold value.
3 Choice model parameter estimation and computation results
In this section, a field test is conducted in Beijing to collect the empirical real-time data of traffic commuting corridors. It should be clarified that the model parameters can be divided into two kinds: time-variant and time-invariant. Thus, we conduct our field measurements from 5:30 a.m. to 11:00 p.m. with a step of 30 min so as to get the whole day’s travel cost.
3.1 Model parameter estimation
As illustrated in Section 2, the scenario is chosen as a traffic commuting corridor serving resident who commutes from suburban Tongzhou District to Guomao CBD. The origin of the studied scenario is set as the residential area of Tongzhou Beiyuan and the destination is set as the Guomao CBD. There are N=10 subway stations along the corridors in length of D=15.5 km. The subway stations are Guomao CBD(1st), Dawanglu(2nd), Sihui(3rd), Sihui East(4th), Gaobeidian(5th), Chuanmei University(6th), Shuangqiao(7th), Guanzhuang(8th), Baliqiao(9th), Tongzhou Beiyuan(10th). In accordance, the studied corridors can be divided into 9 links. The distance of each link are illustrated in Fig. 4.
Then, the field measurement results of travel cost model parameters for expressway mode, subway mode and P&R mode are presented respectively.
As for subway mode, the parameters are measured as 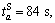

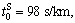

 RMB, ms=0.2
RMB, ms=0.2  RMB/km, Cs=1470; the station-variant parameter
RMB/km, Cs=1470; the station-variant parameter 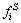 are illustrated in Fig. 5; the scaling parameters of gS(·), are chosen as ω=1, θ=1 [29]. As for the parameter of passenger flow
are illustrated in Fig. 5; the scaling parameters of gS(·), are chosen as ω=1, θ=1 [29]. As for the parameter of passenger flow 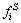 in subway, only the passenger who travels from suburban area to CBD is calculated. That is, the passenger who travels from CBD to suburban area will be ignored in our case.
in subway, only the passenger who travels from suburban area to CBD is calculated. That is, the passenger who travels from CBD to suburban area will be ignored in our case.
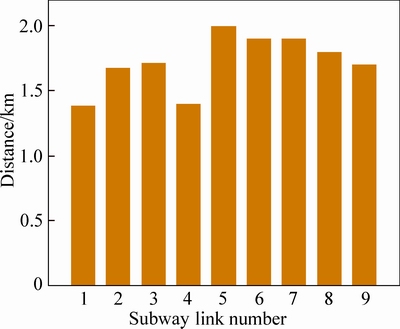
Fig. 4 Distance di between any two stations
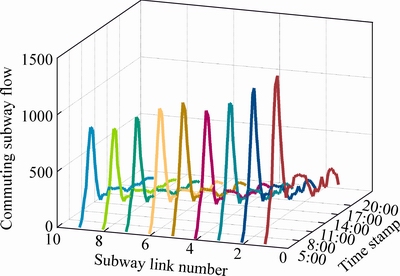
Fig. 5 Distribution of passenger flow 
As for expressway mode, the parameters are measured as  59 s/km,
59 s/km, 105 s,
105 s, 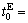 85 s/km,
85 s/km,  1
1  RMB,
RMB, 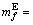 0.7
0.7  RMB/km,
RMB/km, 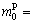 8
8  RMB/h; the time-variant and station-variant parameter
RMB/h; the time-variant and station-variant parameter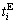 are illustrated in Fig. 6. It is necessary to note that since the value of real-time traffic flow
are illustrated in Fig. 6. It is necessary to note that since the value of real-time traffic flow and road capacity CE is hard to attack, we directly measure the congestion travel time
and road capacity CE is hard to attack, we directly measure the congestion travel time 
As for P&R mode, the station-based parameters 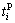 and
and  are illustrated in Fig. 7.
are illustrated in Fig. 7.
Besides, according to the statistics from Beijing Household Travel Survey, the VOT and VOC of Beijing residents are set to be σ=48 RMB/h and λ=30 RMB/unit.
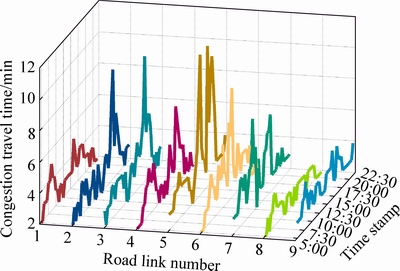
Fig. 6 Congestion travel time 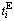
3.2 Generalized travel cost of subway, expressway and P&R mode
Based on the estimated model parameters in Subsection 3.1, the real-time generalized travel cost of different travel modes can be calculated, accordingly. Figure 8 illustrates the generalized travel cost from part of different origins to CBD.
It should be clarified that P&R mode contains more than one generalized travel cost, due to the fact that travellers have multiple transfers to park-and-ride. We assume that all P&R travellers will choose the transfers with a minimum generalized travel cost. Figure 9 shows us a P&R traveller’s generalized travel costs of different P&R transfers who departs from the origin of the 10th station at 9:00 a.m. According to our assumption, this P&R traveller will choose the 7th station to transfer from expressway mode to subway mode.

Fig. 7 Parameters of 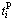 and
and 

Fig. 8 Generalized travel cost of expressway, subway and P&R mode:
Fig. 9 Assumptions of P&R travellers on choice of P&R transfers at 9:00 a.m.
3.3 Computation results of RUT-based and DFT- based choosing probability
Based on the measured parameters, it is capable to estimate the choosing probability of travel modes via the proposed decision theories. Similarly, it is necessary to demonstrate the parameters of RUT and DFT at first.
In our case, the parameters of RUT are set as follows. The error term εη follows the normal distribution with mean of zero and variance of one. The scaling parameter  is assigned to one. Figure 10 illustrates the RUT-based choosing probability of subway, expressway and P&R mode from the origin of the 10th station.
is assigned to one. Figure 10 illustrates the RUT-based choosing probability of subway, expressway and P&R mode from the origin of the 10th station.
Then we determine the parameters of DFT as follows. The error term εη(τ) also follows the normal distribution with mean of zero and variance of one. The self-feedback coefficient sηη is set as 0.9115 based on Ref. [23]. To make a comparison with RUT, the initial preferences Pi(0) for subway, expressway and P&R mode are chosen as the corresponding RUT-based choosing probability. The first stopping criterion is selected to terminate DFT algorithm in our case. The maximum deliberation time is set as Td=30 s.
Fig. 10 Illustration of RUT-based travel mode choice probability
Figure 11(a) shows us the dynamic evolution of the DFT-based mode choice probability. We choose an example of the travellers who departs at 9:30 a.m.. It actually reflects the psychological deliberation process of the decision maker. Similar to the RUT-based theory, Fig. 11(b) illustrates the DFT-based travel mode choice probability. Since the maximum deliberation time is set as 30 s, the choosing probability at 30 s in Fig. 11(a) is chosen as the final DFT-based choosing probability at 9:30 a.m. in Fig. 11(b).

Fig. 11 Illustration of DFT-based travel mode choice probability:
4 Modal choice behaviour analysis in terms of important factors
In Subsection 3.3, we give an illustration of mode choice probability based on RUT and DFT. However, the modal choice behaviour is influenced by many considerable factors, such as trip distance, departure time, income levels. In this section, a set of computational results with the model is presented to illustrate the effects of considerable factors, including travelling distance, traffic flow, VOT and VOC.
4.1 Effects of trip distance
To check the effect of trip distance on corridor mode choice analysis, we measure the number of subway stations that pass to CBD and then sum up the distance of each passing link. Since we have 10 stations in our traffic corridor network, the travel distance of commuting to CBD will increase from the 2nd station to the 10th station. Both RUT-based and DFT-based choosing probabilities of different stations are depicted in Fig. 12.
As for the results, we found that the choosing probability of P&R mode increases with the increase of trip length. Correspondingly, the probability of subway and expressway mode decreases. It indicates the fact that P&R mode is more attractive to longer distance commuters while the expressway mode and subway mode are suitable for shorter distance commuters. The findings may suggest us that subway service does not need to cover the rural areas along the traffic corridor, and the P&R mode may be a more suitable choice for long distance trip.
Fig. 12 Choosing probability distribution with different trip length based on RUT and DFT:
4.2 Effects of traffic flow
Usually, the traffic flow in the commuting corridors is mainly influenced by the departure time of travellers. In the morning peak hours, the traffic corridor suffers from heavy congestion due to high level of traffic flow. While in the non-peak hours, the commuting traffic flow decreases correspondingly. We choose the time point 7:30 a.m. (peak hours) and 12:00 a.m. (non-peak hours) as an representative to check the mode choice behaviour under different levels of traffic flow. Their RUT-based and DFT-based choosing probabilities are illustrated in Fig. 13.
It can be seen that within peak hours, most travellers near the suburban area prefer to drive cars because of its high speed and comfort, while travellers inthe downtown areas prefer to take a subway due to its congestion free property and the escape from high parking fees in the CBD. Whereas, within non-peak hours, the travellers prefer to take a subway because of its relatively low travel cost.
4.3 Effects of VOT and VOC
In our case, the effect of VOT and VOC is studied to characterize the modal choice behaviour of different income level travellers. It is assumed that the parameters of VOT and VOC have an approximate linear relation with traveller’s income [30]. So, we set a scaling parameter rV to represent this linear coefficient. Figure 14 illustrates the choosing probabilities with different VOTs (rVσ, rV=1, 2, 3) and VOCs (rVλ, rV=1, 2, 3).
It displays that with the increment of VOT and VOC, the choosing probability of expressway mode increases, whereas the probability of subway mode decreases. And the probability of P&R mode maintains at a low level. The results show that the high income level travellers are more sensitive to travel comfort issues and prefer to drive their private vehicles as long as possible to avoid the discomfort of subway mode.
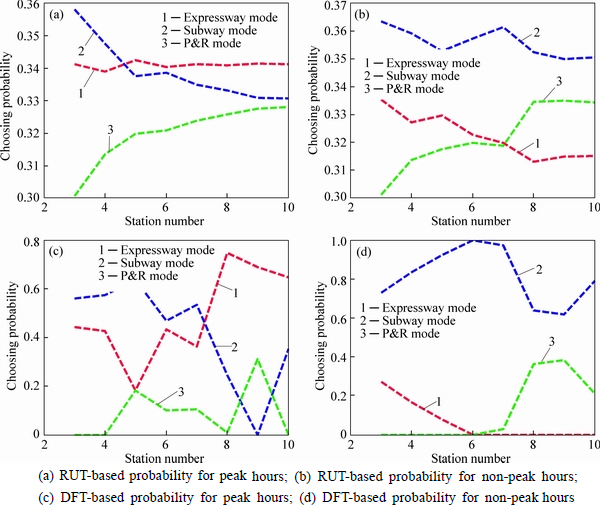
Fig. 13 Choosing probability distribution with different time periods based on RUT and DFT:
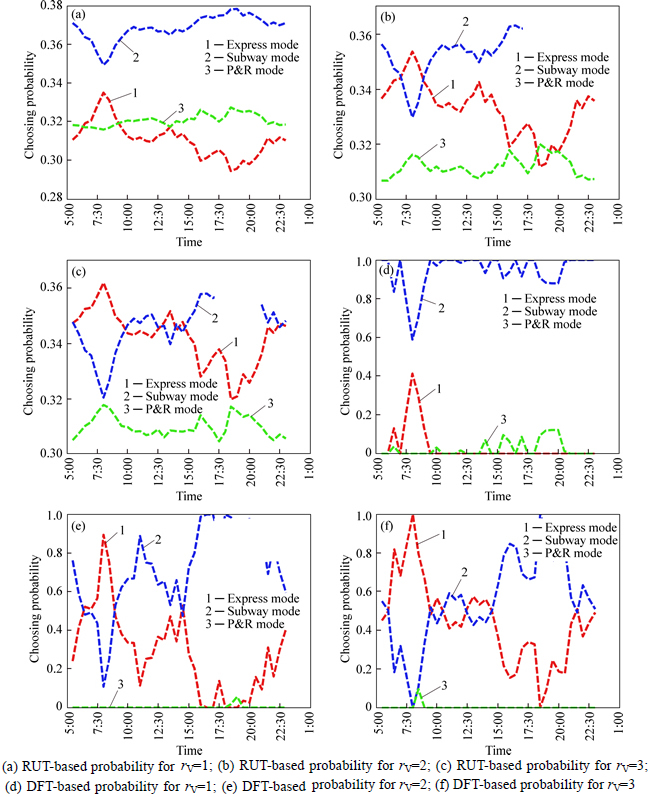
Fig. 14 Choosing probability distribution with different VOT&VOC ratios rV based on RUT and DFT:
5 Conclusions
1) In many cities with multimodal transportation systems, traffic administrators make efforts to enhance the sharing rate of public transit. They make various policies, such as road pricing toll, reducing public transit fares and support P&R parking facilities, to reduce the usage of private vehicles and encourage the usage of public transit. However, it is an urgent need to propose a theoretical model to evaluate how these polices influence the mode choice behaviour of different modes. Therefore, we propose a method to analyze and evaluate the travel mode choice via describing the travel cost of one certain transportation mode’s status in a specific node, link, route or network within different time periods. Two typical decision-theoretical methods were introduced to formulate the traveller’s decision-making process on travel mode choice. Effects on the mode split patterns for some important factors, such as trip length, traffic flow, VOT and VOC, were investigated as well.
2) The new method offers two significant contributions to multimodal transportation system. First, by applying the quantitative models to depict travellers’ generalized travel cost of different modes, we can capture the detailed variability of those modes. Further, the proposed model reling on real-time data is capable to identify the travel costs with different time periods, especially for peak hours and non-peak hours. It helps us to distinguish the diversified modal choice behaviour and then estimate the sharing rate of different travel modes. Second, by applying the decision field theory, we overcome the limitation of classical random utility based decision theories which cannot well depict the psychological deliberation process of human beings. It helps us to approach the more accurate decision making behaviour and explore the real choosing probability.
3) There are also some improvements that can be made to improve our research work. For example, the choosing probability estimated by our proposed model needs to be verified by the real condition. A survey needs to be conducted in the near future to collect more real data so as to validate the correctness and effectiveness of our model.
References
[1] VERPLANKEN B, AARTS H, VAN KNIPPENBERG A. Habit, information acquisition, and the process of making travel mode choices [J]. European Journal of Social Psychology, 1997, 27(5): 539-560.
[2] van SCHIJNDEL W J, DINWOODIE J. Congestion and multimodal transport: a survey of cargo transport operators in the Netherlands [J]. Transport Policy, 2000, 7(4): 231-241.
[3] REHRL K, BRUNTSCH S, MENTZ H J. Assisting multimodal travelers: Design and prototypical implementation of a personal travel companion [J]. IEEE Transactions on Intelligent Transportation Systems, 2007, 8(1): 31-42.
[4] MESCHINI L, GENTILE G, PAPOLA N. A frequency based transit model for dynamic traffic assignment to multimodal networks [C]// Proceedings of 17th International Symposium on Transportation and Traffic Theory. London: Elsevier, 2007.
[5] ZILIASKOPOULOS A, WARDELL W. An intermodal optimum path algorithm for multimodal networks with dynamic arc travel times and switching delays [J]. European Journal of Operational Research, 2000, 125(3): 486-502.
[6] BHAT C R. A heteroscedastic extreme value model of intercity travel mode choice [J]. Transportation Research Part B: Methodological, 1995, 29(6): 471-483.
[7] BHAT C R. Work travel mode choice and number of non-work commute stops [J]. Transportation Research Part B: Methodological, 1997, 31(1): 41-54.
[8] QIAN Z S, ZHANG H M. Modeling multi-modal morning commute in a one-to-one corridor network [J]. Transportation Research Part C: Emerging Technologies, 2011, 19(2): 254-269.
[9] van NES R. Design of multimodal transport networks: A hierarchical approach [M]. TU Delft, Delft University of Technology, 2002.
[10] BANOMYONG R, BERESFORD A K C. Multimodal transport: The case of Laotian garment exporters [J]. International Journal of Physical Distribution & Logistics Management, 2001, 31(9): 663-685..
[11] LO H K, YIP C W, WAN Q K. Modeling competitive multi-modal transit services: A nested logit approach [J]. Transportation Research Part C: Emerging Technologies, 2004, 12(3): 251-272.
[12] MAHMASSANI H S, LIU Y H. Dynamics of commuting decision behaviour under advanced traveller information systems [J]. Transportation Research Part C: Emerging Technologies, 1999, 7(2): 91-107.
[13] ZILIASKOPOULOS A, WARDELL W. An intermodal optimum path algorithm for multimodal networks with dynamic arc travel times and switching delays [J]. European Journal of Operational Research, 2000, 125(3): 486-502.
[14] CASCETTA E. Transportation systems analysis: Models and applications [M]. New York: Springer, 2009.
[15] WILSON A G, COELHO J D, MACGILL S M, WILLIAMS H C. Optimisation in locational and transport analysis [M]. New York: Wiley, 1981.
[16] CANTARELLA G E, DE LUCA S. Multilayer feedforward networks for transportation mode choice analysis: An analysis and a comparison with random utility models [J]. Transportation Research Part C: Emerging Technologies, 2005, 13(2): 121-155.
[17] BUSEMEYER J R, TOWNSEND J T. Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment [J]. Psychological Review, 1993, 100(3): 432-459.
[18] WU J, SUN H, WANG D Z W, ZHANG M, HAN L, GAO Z. Bounded-rationality based day-to-day evolution model for travel behavior analysis of urban railway network [J]. Transportation Research Part C: Emerging Technologies, 2013, 31: 73-82.
[19] ZHAO H, YAN X, GAO Z. Transportation serviceability analysis for metropolitan commuting corridors based on modal choice modelling [J]. Transportation Research Part A: Policy and Practice, 2013, 49: 270-284.
[20] WANG R. Autos, transit and bicycles: Comparing the costs in large Chinese cities [J]. Transport policy, 2011, 18(1): 139-146.
[21] ZHENG Y, GUO W, ZHANG Y, HU J. A generalized comfort function of subway systems based on a nested logit model [J]. Tsinghua Science and Technology, 2014, 19(3): 300-306.
[22] MONGIN P. Expected utility theory [M]// Handbook of Economic Methodology. Cheltenham: Edward Elgar Publishing, 1997: 342-350.
[23] QIN H, GUAN H, WU Y J. Analysis of park-and-ride decision behavior based on decision field theory [J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2013, 18: 199-212.
[24] BUSEMEYER J R, JOHNSON J G. Micro-process models of decision making [M]. Cambridge: Handbook of Computational Psychology, 2008.
[25] ROE R M, BUSEMEYER J R, TOWNSEND J T. Multialternative decision field theory: A dynamic connectionst model of decision making [J]. Psychological Review, 2001, 108(2): 370-392.
[26] BUSEMEYER J R, DIEDERICH A. Survey of decision field theory [J]. Mathematical Social Sciences, 2002, 43(3): 345-370.
[27] BUSEMEYER J R, JOHNSON J G. Computational models of decision making [M]. Blackwell: Handbook of Judgment and Decision Making, 2004: 133-154.
[28] DUAN K, LI J Y. The application of decision field theory in clothing style evaluation [J]. Journal of Donghua University: Natural Science, 2010, 36(2): 175-178. (in Chinese)
[29] GOODMAN C J, MURATA S. Metro traffic regulation from the passenger perspective [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2001, 215(2): 137-147.
[30] LAM T C, SMALL K A. The value of time and reliability: Measurement from a value pricing experiment [J]. Transportation Research Part E: Logistics and Transportation Review, 2001, 37(2): 231-251.
(Edited by YANG Hua)
Foundation item: Project(2012CB725405) supported in part by National Basic Research Program of China; Project(2014BAG03B01) supported by the National Science and Technology Support Program, China; Project(71301083) supported by the National Natural Science Foundation of China; Project(20131089307) supported by the Project Supported by Tsinghua University, China
Received date: 2015-06-23; Accepted date: 2015-11-19
Corresponding author: ZHANG Yi, Professor; Tel: +86-10-62796832; E-mail: zhyi@tsinghua.edu.cn

