J. Cent. South Univ. (2020) 27: 1802-1813

DOI: https://doi.org/10.1007/s11771-020-4409-8

Aerodynamic noise characteristics of high-speed train foremost bogie section

LIANG Xi-feng(梁习锋)^{1, 2, 3}, LIU Hui-fang(刘慧芳)^{1, 2, 3}, DONG Tian-yun(董天韵)^{1, 2, 3},

YANG Zhi-gang(杨志刚)^{1, 2, 3}, TAN Xiao-ming(谭晓明)⁴

1. Key Laboratory of Traffic Safety on Track, Central South University, Ministry of Education,Changsha 410075, China;

2. Joint International Research Laboratory of Key Technologies for Rail Traffic Safety,Changsha 410075, China;

3. National and Local Joint Engineering Research Center of Safety Technology for Rail Vehicle,Changsha 410075, China;

4. School of Automotive and Transportation Engineering, Hefei University of Technology,Hefei 230009, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: This paper investigates the main scale analysis of the aerodynamic noise in the foremost bogie area by the large-eddy simulation (LES) and the Ffowcs Williams-Hawkings (FW-H) analogy. The mechanism of the aerodynamic noise in this area has been excavated. The aerodynamic excitation results show that the bogie divides the bogie compartment into two cavities, each of which contains a large circulating flow and presents multi-peak characteristics in the frequency domain. The far-field noise results suggest that in the speed range of 200-350 km/h, the aerodynamic noise mechanism in the bogie area is the same. Cavity noise is the main noise mechanism in the foremost bogie area, and the bogie divides the bogie cabin into two cavities, thereby changing the aerodynamic noise in this area.

Key words: large-eddy simulation; high-speed train; flow-field structure; aerodynamic noise; bogie

Cite this article as: LIANG Xi-feng, LIU Hui-fang, DONG Tian-yun, YANG Zhi-gang, TAN Xiao-ming. Aerodynamic noise characteristics of high-speed train foremost Bogie section [J]. Journal of Central South University, 2020, 27(6): 1802-1813. DOI: https://doi.org/10.1007/s11771-020-4409-8.

1 Introduction

At present, China’s high-speed trains run at a speed of 300 km/h and are expanding to 400 km/h [1, 2]. However, with the increase of running speed, the noise problem of high-speed trains becomes more and more significant. When the high-speed train is running at 300 km/h, the aerodynamic noise will be greater than the wheel-rail noise, and becomes the main type [3]. Relevant research show that the bogie area is the main aerodynamic noise source of high-speed train [4], and the aerodynamic noise of the foremost bogie area is the strongest in all the bogie areas.

The bogie area includes the Couette flow of the train bottom moving relative to the ground, the rod flow of the bogie, the cavity flow of the bogie cavity, etc. This makes the flow field in the bogie area quite complex. Currently, the research methods of aerodynamic noise in the bogie area mainly include experiments and numerical simulations.

Comprehensive achievements have been made by researchers with corresponding experiments. For example, FREMION et al [5] analyzed the aerodynamic noise characteristics of the full-scale Train à Grande Vitesse (TGV) train bogie areas in France by using coherent output power technology, and it is found that the bogie area had a variety of incoherent sound sources, the sound source at the bottom of the bogie was not significantly radiated outwards. The sound source at the upstream and downstream of the wheel arch cover was significantly radiated outwards, the main frequency distribution range is 500-1000 Hz. The spectrum of the sound source intensity downstream of the wheel arch appears multiple peak frequencies around 600 Hz. TAN et al [6] used the spectrum fitting method based on the frequency similarity criterion and the strength similarity criterion to separate the wheel-rail noise and the aerodynamic noise in the bogie area of high-speed train, performed the proportion analysis of the wheel-rail noise vs the aerodynamic noise at different operating speeds, and found that 300 km/h was the bogie area acoustics conversion speed. SONG et al [7] used the operation transfer path analysis (OTPA) technique to separate the wheel-rail noise and the aerodynamic noise in the trailer bogie area of high-speed train during a field test, and then analyzed their respective strength and spectrum characteristics, and got the following conclusion: the low-frequency noise in the trailer bogie area mainly comes from the wheel-rail noise, while the mid-to-high frequency noise mainly comes from the aerodynamic noise. Tests [8] were performed in the large-scale low-noise anechoic wind tunnel at Maibara, Japan used a 1:7 scale train car and bogie model to investigate the influence factors of the aerodynamic noise in the bogie area of the high-speed train, including the shape of the bogie cavity, different parts of the bogie, the arrangement of the skirts, and the boundary layer on the ground. The results indicate that the bogie cavity with the arc-shaped leading edge and the side skirt can effectively reduce the aerodynamic noise generated by itself. The aerodynamic noise in the upstream bogie area is greater than that in the downstream bogie area. The noise at the trailing edge of bogie cavity is larger than that at the leading edge. LAUTERBACH et al [9] performed an experimental study on the aerodynamic noise Reynolds number effect of the high-speed trains (a 1:25 scale model), and found that the aerodynamic noise in the bogie area was mainly distributed below 5000 Hz, which can be described by cavity excitation model.

In terms of numerical simulations, MINELLI et al [10] performed an aero-acoustic numeric study of the flow surrounding the bogie cavity, and found that the aerodynamic flow field around the bogie cavity is dominated by two main structures, the jet flow created by the gap clearance between the snowplow and the ground and the shear flow detached from the curvature of the front snowplow. ZHU et al [11] utilized the delayed detached-eddy simulation (DDES) model and the FW-H equation to study the flow field and aerodynamic noise characteristics of a simple bogie composed of wheel sets, axles and frames, and discovered that the peak noise came from the axles, the contribution rate of the frame to the total noise is lower than that of the wheel sets, the aerodynamic noise of the front wheels presents the lift dipole characteristics, the aerodynamic noise of the rear wheels is characterized by a lift dipole and a drag dipole. MASSON et al [12] applied the lattice Boltzmann method [13] to investigate the aerodynamic noise of the bogie areas, and the results demonstrated that the foremost bogie area in the head-car was the most dominant source of noise in all bogies. LIU et al [14] employed the DDES model and the Fowcs Williams-Hawking (FW-H) equations to study the effects of Reynolds number on the flow field and sound field in the subcritical region and critical region, and the finding is that the peak Strouhal number (St), the aerodynamic coefficient and the aerodynamic noise (excluding velocity effect) in the subcritical region did not change much, but they changed significantly in the critical region. ZHANG et al [15] performed a numerical study on the aerodynamic noise of the power bogie, and it can be concluded that the contribution rate of the frame to the total noise was the largest among all components.

Based on the above literature research, the following problems can be found in the research of aerodynamic noise in bogie area. In the field test, the separation of wheel-rail noise and aerodynamic noise is the first problem to be solved. Although a variety of separation technologies have been proposed at present, they all have unavoidable defects, which make their results quite different. For example, TAN et al [16] drew the conclusion that the aerodynamic noise in bogie area is mainly distributed in low frequency range relative to wheel-rail noise, while SONG et al [7] reached the opposite conclusion. In the acoustic wind tunnel test, the ground is still, which makes the flow field of bogie area different from the real flow field. In the numerical study, the research object is mainly focused on a simplified component, and the complex bogies in the real operating environment are not used; the research conclusions are mainly focused on the spectrum and directivity characteristics of aerodynamic noise, and the main scale analysis of aerodynamic noise is not involved.

Differing from the mentioned investigations, this paper does not focus on the problems in the field test and the acoustic wind tunnel test, but intends to use the numerical method to perform the main scale analysis of the aerodynamic noise in the bogie area, and then excavates the mechanism of the aerodynamic noise in this area. The geometry of all bogie areas in this simulation is the same, which makes them have similar aerodynamic noise mechanism. However, the underbody boundary layer effect changes their inflow velocity amplitude and turbulence, which in return changes their aerodynamic noise intensity. The foremost bogie area has the fastest incoming flow. For the sake of generality, the main scales of aerodynamic noise in the foremost bogie area are excavated as an example. Therefore, the structure of this paper is as follows: the second part is the numerical calculation model, the third part is the calculation results, the fourth part is the discussion, and the fifth part is the conclusions.

2 Numerical computation model

Take a 1:8th-scale high-speed train including three cars (namely 3-train formation) and six sets of bogies as the computational model, see Figure 1. The bogie geometry is simplified but the general shape is presented [17]. The 3-trian formation model was used often in engineering because it is the most simplified model that can truly reflect the actual 8-section formation [18]. On the other hand, there are only test data of noise radiation from 3-car model in openly available data so the simulation results can be verified. The length, width and height of the train model are 10.044, 0.420 and 0.507 m, respectively.

The dimensions of the computational domain are 50 m×3.75 m×2.5 m. The geometric dimension descriptions used in this article are all under the 1:8-scale model. The train model is placed at the central position in the span-wise direction, with a vertical distance of 0.025 m from the ground. The entry boundary in front of the train head is set as velocity inlet boundary, while the exit boundary behind the train tail is chosen as pressure outlet boundary. The upper side, the left and the right sides are set as symmetrical boundaries. Besides, the ground effects are simulated by setting the ground as the slip ground with a velocity equal to the incoming flow velocity.

The commercial software ICEM CFD was adopted to mesh grids. The computational grid is further optimized on the basis of grid division [16]. For example, the grid size of the whole underbody area is refined to less than 5 mm. The amount of meshes is about 1.1×10⁸. Figures 1(b) and (c) show the grid distribution on the surface of the bogie and around the bogie, respectively.

In general, the refiner grid in the boundary layer and the space are two essential requirements of the LES. The parameter to measure the mesh in boundary layer is y⁺ [19] (see Eq. (1)). The spatial mesh distribution parameter is l_△/l_t [16], where l_t is the local integral scale, and l_△ is the equivalent length of the spatial mesh.

                              (1)

whereis the wall friction velocity; τ_ω is the wall shear stress; y is the distance from the centroid of the firs layer of mesh to the wall; υ is the kinematic viscosity coefficient.

Figure 1 Model and mesh distribution:

The local integral scale is defined as:

l_t=C₀k^3/2/ε                               (2)

where C₀=0.2, k is the turbulence energy, and ε is the turbulence dissipation rate.

The equivalent length of the spatial mesh is defined as

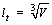                                (3)

where V is the volume of the mesh.

Figures 2 and 3 show the y⁺ distribution on the train components and the l_△/l_t distribution in computational domain, respectively. They are both lower than 1, which means that the mesh schemes are fine and adequate for LES model. The LES is applied in this paper instead of the hybrid method, which has been widely used in the research of train aerodynamics [20, 22]. This is because the LES resolves the boundary layer instead of model it,thus provides a more accurate solution.

The CFD simulation was conducted by the ANSYS FLUENT from the National Supercomputing Center in Wuxi, China. To ensure the stability of the LES, the realizable k-ε turbulence model is chosen in the steady computation and the enhanced wall treatment method is used for the near wall face. The Smagorinsky-Lilly-based turbulence model is adopted for the transient flow field computation [23, 24]. Besides, PISO algorithm is employed for the pressure-velocity coupling terms. The bounded central differencing is used to separate the momentum terms. The second-order implicit scheme is employed for the temporal difference equation. The transient flow computation provides acoustic sources. The far-field noise predictions were computed by the FW-H acoustic analogy [25]. The unsteady calculation time step was 5×10^-5 s. The Courant–Friedrichs–Lewy number (CFL= u△t/△x, u is velocity) is less than 1. Each time step includes 30 iterations. A total of 10000 time steps were calculated.

The grid generation, turbulence model and boundary conditions used here were validated [16], where the same numerical method was adopted to calculate the far-field radiated noise of a high-speed train. The results were verified by comparison with the test data in anechoic wind tunnel.

Figure 2 y⁺ distribution of power car (a), foremost bogie of power car (b), and tail of train (c) (incoming flow speed v=350 km/h)

Figure 3 Spatial distribution of l_△/l_t in horizontal plane cut at z=0.05 m

3 Results

3.1 Characteristics of aerodynamic excitation

The free inflow velocities of the numerical include 200, 250, 300 and 350 km/h. The corresponding Reynolds numbers are the order of magnitude 6 (10⁶) based on the height of the model. Therefore, in this speed range, the flow field in the foremost bogie area is located in the range of subsonic and high Reynolds number, and the corresponding aerodynamic excitation characteristics are similar. In the following, the aerodynamic excitation characteristics in the foremost bogie area at 350 km/h are discussed as an example. Figures 4 and 5 present the distributions of instantaneous velocity and vorticity magnitude, respectively, in the vertical mid-plane (y=0 m) and the horizontal plane at z=0.05 m. Figure 6 shows the instantaneous vortex structure around the foremost bogie based on Q-criterion [23] (defined by Eq. (4）,with a Q-value of 200000),which is colored by the vorticity magnitude. The animation made by Figure 4(a) at different moments and the animation made by Figure 5(a) at different moments can be found in supplementary files 1 and 2, respectively.

                          (4)

where || || is the second norm of the tensor; Ω is the vortex tensor, composed of the anti-symmetric part of the velocity gradient tensor; S is the strain rate tensor, composed of the symmetric part of the velocity tensor.

According to Figures 4-6 and the above 2 animations, the flow under the train bottom is similar to the jet flow in the Laval nozzle, changes violently due to the narrow space, and produces the complicated flow structures here. On the whole, this flow can be divided into two parts: up and down. The up part is close to the train bottom, and is a low-speed, strong-vorticity airflow. The down part is close to the ground, and it is a high-speed, weak-vorticity airflow. The boundary between the two parts is not a straight line because of the disturbances of the snow-plough and the foremost bogie. Downstream the snow-plough, this boundary is a continuous wave. Under the foremost bogie, this boundary is divided into sections.

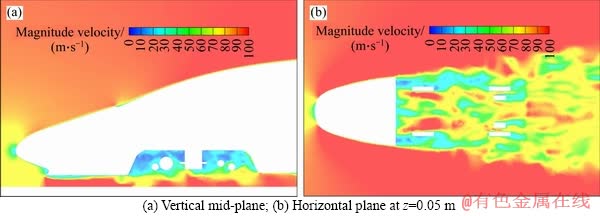
Figure 4 Velocity distribution around train:

Figure 5 Vorticity distribution around train:

Figure 6 Instantaneous vortex structure distribution

The flow field around the foremost bogie mainly includes 2 large circulating flows. The first circulating flow is between the leading edge of the cavity and the middle boxes of the bogie (the location of the middle boxes is shown in Figure 8). The second circulating flow is between the middle boxes of the bogie and the tail edge of the cavity. There are also smaller scale circulating flows in each circulating flow. Compared with the first circulating flow, the second circulating flow has stronger aerodynamic excitation intensity.

At the leading edge of the foremost bogie cavity, the shear flow is low-speed, strong-vorticity, and is divided into sections by the first circulating flow. This shear flow travels downstream, hits the front end of the middle boxes, and is divided into two parts. One part flows into the bottom of the cavity, and participates in the first circulating flow. The other part is attached to the bottom of the middle boxes, and becomes a new shear flow when leaving the rear end of the middle boxes. When the new shear flow flows downstream, it is affected by the second circulating flow and fluctuates up and down. When the shear flow fluctuates upward, it can impact the rear axle. When the shear flow fluctuates downward, it can approach the ground. Finally, the new shear flow crashes into the rear wall of the cavity and is divided into two parts. One-part flows downstream. The other part flows to the bottom of the cavity, and participates in the second circulating flow.

These flows create a lot of large-scale single-pin hairpin vortices around the foremost bogie. The hairpin vortices overflow on two sides of the cavity and grow along the side wall of the train body, which leads to larger single-pin hairpin vortices. Compared with the interior of the cavity, the vortex structure on the exterior of the cavity has a large scale.

Figure 7 shows a series of instantaneous vorticity magnitude contours at different time on the cavity mid-span surface. According to Figures 7(a)-(f), the strong periodical vortex shedding occurs at the leading-edge of the cavity, and then the vortices transport downstream, some of them are broken down by the bogie components. The vorticity fluctuations come from the shear layer and get amplified in the downstream direction. The approximate period of this cycle is 0.0015-0.0025 s, and the vortex shedding frequency can be estimated to be 400-667 Hz. Obvious vortex shedding from the cylindrical components is not observed.

Figure 8 shows the names of the main components of the bogie and the locations of the monitoring points. These 10 receiving points are arranged at the cavity mid-span, every 0.05 m in the x-direction.

The dimensionless power spectral density analysis of the velocity amplitude at these 10 measuring points is shown in Figure 9. The power density function E_u of u is calculated using the FFT algorithm. The reference value of speed amplitude power at each point is the total power at the corresponding point. Hanning window was used for the power spectrum analysis. The overlap rate of Hanning window is 60%. The analysis frequency range is 0-10 kHz. The frequency resolution is 20 Hz.

According to the similarity degree of power spectral density curve, these curves at 10 measuring points in Figure 9 can be divided into three categories: 1-4 measuring points, 5 and 6 measuring points, and 7-10 measuring points. Measuring points 1-4 are between the leading edge of the cavity and the middle boxes of the bogie. Measuring points 5 and 6 are located under the middle box of the bogie. Measuring points 7-10 are between the middle boxes of the bogie and the tail edge of the cavity. Combined with the above flow field structure analysis, measuring points 1-4 reflect the characteristics of the first circulating flow, measuring points 7-10 reflect the characteristics of the second circulation flow, measuring points 5 and 6 reflect the characteristics of their transition. The power spectral curves at these 10 measuring points all show multi peak characteristics. Their peak frequencies are shown in Figure 9. These peak frequencies will be further analyzed in combination with sound field results.

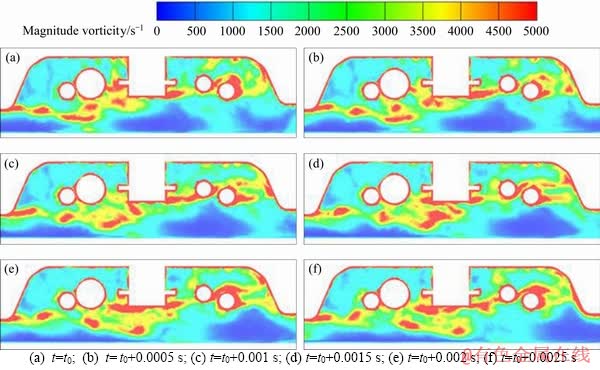
Figure 7 Vorticity magnitude contours at cavity mid-span at six different instants (v=350 km/h):

Figure 8 Schematic diagram of bogie and measuring points

3.2 Far-field radiation noise characters

According to the ISO3095-2013 standard, the receiving points are arranged 0.4375 m above the ground (z=0.4375 m) and 3.125 m away from the center line of the train (y=3.125 m), as shown in Figure 10. The total number of measuring points is 16, and the points are arranged every 0.625 m in the x-direction.

Figure 11 shows the spectrum of the sound pressure level at Point 2 radiated by the foremost bogie area (divided into the bogie and the cavity). Its related parameters, such as window function, window overlap ratio and frequency resolution, are consistent with the parameters of Figure 9. In the 200-350 km/h operating speed range, the sound pressure level spectrum curves of the foremost bogie area have a high degree of similarity, which are mainly distributed in the range of 100-1000 Hz.

In order to consider the directivity of acoustic radiation, the sound pressure levels of the 16 measuring points in Figure 10 are calculated by formulas (5) and (6) to obtain the average equivalent radiated acoustic energy density, I_average.

I_i=10^SPL_i^/10                                                 (5)

                          (6)

Figure 9 Speed amplitude power spectral density curves at 10 mearing points (incoming flow speed v=350 km/h)

Figure 10 Locations of aerodynamic noise observers parallel to central line

where I is the equivalent radiated acoustic energy density; SPL is the sound pressure level; the subscript i represents the serial number of the measuring point.

Figure 11 Sound pressure level (SPL) spectrum curves at Point 2 radiated by foremost bogie and cavity

Based on I_average, Table 1 summarizes the ratio of the sound energy of the bogie and the cavity to the foremost bogie area. In the foremost bogie area, the radiated acoustic energy of the cavity is slightly more than that of the bogie.

Table 1 Statistical table of radiated acoustic energy (foremost bogie area)

Figures 12(a) and (b) show the dimensionless spectrum (1/3 octave) of I_average radiated from the foremost bogie and its cavity, respectively. The reference value of sound energy for each band is the total sound energy. In the speed range of 200-350 km/h, their spectra are relatively similar, displaying the characteristics of broadband and peak. Their peak frequencies are shown in Figure 12. This indicates that the aerodynamic sound mechanism in the foremost bogie area should be consistent in this speed range.

4 Discussion: Noise production mechanism of foremost bogie area

According to the geometric type, the foremost bogie area components can be divided into two types of structures: cavity and rod. The cavity and the rod are both strong aerodynamic sound generators. Whether the aerodynamic noise in the foremost bogie area is dominated by the cavity, rod, or both is the focus of this section.

Figure 12 Dimensionless spectrum (1/3 octave) of I_average:

Concerning the above discussion results of the aerodynamic excitation, the flow field in the foremost bogie area is divided into two major circulating flows, and their energy suppliers are the low-velocity, strong-vorticity shear flow detached from the plate. Shear flow oscillation is the main mechanism of cavity aerodynamic noise [26]. Therefore, it can be preliminarily determined that the cavity is one of the main aerodynamic sound generators in the bogie area.

The cylindrical components of the bogie include axles, wheels, bellows, and brake discs, and their diameters are 29, 108, 55 and 30 mm, respectively. When the airflow flows through the cylindrical parts, if the Reynolds number is in the high Reynolds number region, the cylindrical radiated noise should exhibit a “peak” characteristic where the Strouhal number is approximately 0.2. Because their Reynolds numbers are the order of 10⁵, which corresponds to the high Reynolds number domain, the peak frequency for different flow speeds can be calculated using formula (7). It should be noted that the results presented in Table 2 are derived using the airflow velocity in the main stream as the inflow velocity. However, the airflow velocity in the bogie region is generally less than half of that in main stream. Therefore, if the component interference is not considered, their peak frequency should be 0.5 times the results presented in Table 2, that is, it should be less than 336 Hz. However, at the inflow velocity of 200,250, 300 and 350 km/h, the dimensionless I_average spectrums do not have peak frequencies below 336 Hz, which indicates that the rod components do not generate the harmonic noise. In addition, no significant vortex street structure was found in the wake area of the rod. Finally, the shear flow detached from the rods coming from the upstream shear flow. Therefore, the rod is not the main aerodynamic sound generator in the bogie area, but it has some interference effect on the aerodynamic sound in this area.

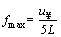                               (7)

where L is the diameter of the cylinder.

Table 2 Peak frequency of bogie cylindrical components

ROSSITER [26] and ROCKWELL et al [27] considered that the shear flow upstream of the cavity deviated from the leading edge, impinged on the tail edge, and created a pressure feedback phenomenon that amplifies the shear layer disturbances in selective frequencies. The self-sustained oscillation of the cavity can be divided into three types: dynamic oscillation, resonance oscillation, and elastic oscillation [27]. The fluid elastic oscillations should not appear because the train model is treated as rigid and solid, and only dynamic and resonance oscillations may occur. The fluid-resonant oscillation can not be essentially simulated without considering the compressibility effect of the flow [28].

The sizes of the bogie cavity are approximately 525 mm in the length, 363 mm in width, and 100 mm in depth, respectively. The first circulating flow was 226 mm in length. The second circulating flow was 231 mm in length. Adopting Rossiter’s semi-empirical formula of cavity fluid dynamic oscillation frequency [29] (see Eq. (8)), the fluid dynamic oscillation frequency of the cavity is calculated. It should be noted that there may be some deviations in the peak frequencies of the noise spectra of the bogie and bogie cavity between the computed results and the semi- empirical data. This discrepancy could be partially ascribed to the inaccuracy of Rossiter’s semi- empirical formula in low Mach number [30] and complex configurations.

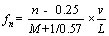                        (8)

where f_n is the frequency of the nth mode, n=1, 2, …; v is inflow speed; L is the cavity length; M is the free stream Mach number.

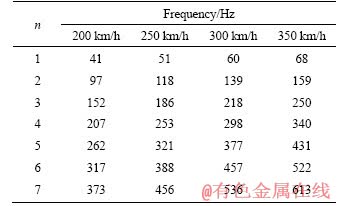
Comparing the fluid dynamic oscillations frequencies in Tables 3-5 with the peak frequency and Figure 12, it can be found that the 2nd and 3rd mode dynamic oscillations frequencies (listed in Tables 3 and 4, respectively) in the first and second circulating flows are in the range of the peak frequencies band in Figure 12, and the 6th and 7th mode frequencies in Table 5 are in the range of the peak frequency band. The 2nd and 3rd mode frequencies are more reasonable. The results tend to demonstrate that the two circulating flows divided by the middle boxes of the bogie dominate the aerodynamic noise in the bogie area. To further confirm this, the flow field and sound field results of the case in 350 km/h are compared. In Figure 9, the dimensionless velocity power spectrum of the first circulating flow contains multiple peak frequencies, where the peak at 380 Hz is significantly larger than other peaks; for the second circulating flow, it also contains multiple peak frequencies, where the peak at 400 Hz is significantly larger than the other peaks. In Figure 12, 400 Hz is the peak frequency octave band of the dimensionless I_average spectrum. The peaks of the dimensionless velocity power spectrum are coincident with the peak frequency band of the dimensionless I_average spectrum. The above results indeed indicate that it is more reasonable to treat the bogie cabin as two cavities when paying attention to the aerodynamic sound of the bogie section.

Table 3 Frequencies of dynamic oscillations for first circulating flow (L=226 mm)

Table 4 Frequencies of dynamic oscillations for second circulating flow (L=363 mm)

Table 5 Frequencies of dynamic oscillations for whole cavity (L=525 mm)

Combining these results, it can be confirmed that the cavity dominates the aerodynamic noise in the bogie area, and the bogie divides the cavity into two, thereby changing the aerodynamic noise in the bogie area.

5 Conclusions

In this study, the LES is applied to simulating the fluctuating flow fields in the foremost bogie area. Then the FW-H method is used to calculate the far-field aerodynamic noise. Finally, the aerodynamic excitation and noise in the foremost bogie area are used to discuss the aerodynamic noise mechanism in this area. The specific conclusions are as follows.

1) The flow field in the foremost bogie area is divided into two by the middle box of the bogie, and each part is mainly composed of a large circulating flow. Their energy suppliers are the low-velocity, strong-vorticity shear flow detached from the plate. Each circulating flow produces a large number of multi-scale vortex structures.

2) In the speed range of 200-350 km/h, the far-field noise spectrum of the foremost bogie area is similar, mainly distributed in the range of 100- 1000 Hz. In this area, the radiated sound energy of the bogie is slightly less than that of the bogie cabin.

3) The main geometric types causing aerodynamic noise from a bogie is identified. The cavity dominates the aerodynamic noise in the foremost bogie area, and the bogie divides the cavity into two, thereby changing the aerodynamic noise in the bogie area.

Supplementary files

File 1            File 2

References

[1] TAN Xiao-ming, WANG Tian-tian, QIAN Bo-sen, QIN Bin, LU Yi-bin. Aerodynamic noise simulation and quadrupole noise problem of 600 km/h high-speed train [J]. IEEE Access, 2019, 7: 124866-124875. DOI: 10.1109/ACCESS. 2019.2939023.

[2] MAO Yi-qian, YANG Ming-zhi, WANG Tian-tian, WU Fan, Qian Bo-sen. Influence of vacuum level on heat transfer characteristics of maglev levitation electromagnet module [J]. Applied Sciences, 2020, 10(3): 1106. DOI: 10.3390/ app10031106.

[3] DENG Yong-quan, XIAO Xin-biao, HE Bin, JIN Xue-song. Analysis of external noise spectrum of high-speed railway [J]. Journal of Central South University, 2014, 21(12): 4753-4761. DOI: 10.1007/s11771-014-2485-3.

[4] ZHANG Xun, LIU Rui, CAO Zhi-yang, Wang Xi-yang, LI Xiao-zhen. Acoustic performance of a semi-closed noise barrier installed on a high-speed railway bridge: Measurement and analysis considering actual service conditions [J]. Measurement, 2019, 138: 386-399. DOI: 10.1016/j.measurement.2019.02.030.

[5] FREMION N, VINCENT N, JACOB M, ROBERT G, LOUISOT A, GUERRAND S. Aerodynamic noise radiated by the intercoach spacing and the bogie of a high-speed train [J]. Journal of Sound and Vibration, 2000, 231(3): 577-593. DOI: 10.1006/jsvi.1999.2546.

[6] TAN Xiao-ming, YANG Zhi-gang, WU Xiao-long, HE Jiao, ZHANG Dai-jiao, PENG Yong. Experimental research on frequency spectrum component model of noise source outside the CIT500 train [J]. Journal of the China Railway Society, 2017(7): 32-37. (in Chinese)

[7] SONG Lei-ming, CHEN Hao, LI Bao-chuan. Aerodynamic noise separation of an EMU trailer bogie area using train operation tests [J]. Shock and Vibration, 2018, 2018: 1-10. DOI: 10.1155/2018/7941980.

[8] IGLEIAS E L, THOMPSON D J, SMITH M, KITAGAWA T, YAMAZAKI N. Anechoic wind tunnel tests on high-speed train bogie aerodynamic noise [J]. International Journal of Rail Transportation, 2017, 5(2): 87-109. DOI: 10.1080/ 23248378.2016.1274685.

[9] LAUTERBACH A, EHRENFRIED K, LOOSE S, WAGNER C. Microphone array wind tunnel measurements of Reynolds number effects in high-speed train aeroacoustics [J]. International Journal of Aeroacoustics, 2012, 11(3, 4): 411-446. DOI: 10.1260/1475-472X.11.3-4.411.

[10] MINELLI G, YAO H D, ANSERSSON N, HOSMAD P, FORSSEN J, KRAJNOVIC S. An aeroacoustic study of the flow surrounding the front of a simplified ICE3 high-speed train model [J]. Applied Acoustics, 2020, 160: UNSP 107125. DOI: 10.1016/j.apacoust.2019.107125.

[11] ZHU Jian-yue, HU Zhi-wei, THOMPSON D J. Flow behaviour and aeroacoustic characteristics of a simplified high-speed train bogie [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016, 230(7): 1642-1658. DOI: 10.1177/09544097 15605129.

[12] MASSON E, PARADOT N, ALLAIN E. The numerical prediction of the aerodynamic noise of the TGV POS high-speed train power car [C]// 10th International Workshop on Railway Noise (IWRN 2010). Tokyo, Japan: Springer, 2012: 437-444.

[13] LALLEMAND P, LUO Li-shi. Lattice Boltzmann equation with overset method for moving objects in two-dimensional flows [J]. Journal of Computational Physics, 2020, 407: 109223. DOI: 10.1016/j.jcp.2019.109223.

[14] LIU Xiao-wan, THOMPSON D J, HU Zhi-wei. Numerical investigation of aerodynamic noise generated by circular cylinders in cross-flow at Reynolds numbers in the upper subcritical and critical regimes [J]. International Journal of Aeroacoustics, 2019, 18(4, 5): 470-495. DOI: 10.1177/ 1475472X19858348.

[15] ZHANG Ya-dong, ZHANG Ji-ye, ZHANG Liang, LI Tian. Numerical analysis of aerodynamic noise of motor car bogie for high-speed trains [J]. Journal of Southwest Jiaotong University, 2016, 51(5): 870-877. (in Chinese)

[16] TAN Xiao-ming, LIU Hui-fang, YANG Zhi-gang, ZHANG Jie, WANG Zhong-gang, WU Yu-wei. Characteristics and mechanics analysis of aerodynamic noise source for high-speed train in tunnel [J]. Complexity, 2018(7): 1-19. DOI: 10.1155/2018/5858415.

[17] DONG Tian-yun, LIANG Xi-feng, KRAJNOVIC S, XIONG Xiao-hui, ZHOU Wei. Effects of simplifying train bogies on surrounding flow and aerodynamic forces [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 191: 170-182. DOI: 10.1016/j.jweia.2019.06.006.

[18] LI Xue-liang, WU Fan, TAO Yu, YANG Ming-zhi, NEWMAN R, VAINCHTEIN D. Numerical study of the air flow through an air-conditioning unit on high-speed trains [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 187: 26-35. DOI: 10.1016/j.jweia. 2019.01.015.

[19] HODARA J, SMITH M. Hybrid reynolds-averaged navier-stokes/large-eddy simulation closure for separated transitional flows [J]. AIAA Journal, 2017, 55(6): 1948-1958. DOI: 10.2514/1.J055475

[20] WANG Jia-bin, MINELLI G, DONG Tian-yun, CHEN Guang, KRAJNOVIC S. The effect of bogie fairings on the slipstream and wake flow of a high-speed train. An IDDES study [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 191: 183-202. DOI: 10.1016/j.jweia. 2019.06.010.

[21] CHEN Guang, LI Xiao-bai, LIU Zhen, ZHOU Dan, WANG Zhe, LIANG Xi-feng, KRAJNOVIC S. Dynamic analysis of the effect of nose length on train aerodynamic performance [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 184: 198-208. DOI: 10.1016/j.jweia. 2018.11.021.

[22] LI Xiao-bai, CHEN Guang, WANG Zhe, XIONG Xiao-hui, LIANG Xi-feng, YIN Jing. Dynamic analysis of the flow fields around single- and double-unit trains [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 188: 136-150. DOI: 10.1016/j.jweia.2019.02.015.

[23] TAN Xiao-ming, YANG Zhi-gang, TAN Xi-ming, WU Xiao-long, ZHANG Jie. Vortex structures and aeroacoustic performance of the flow field of the pantograph [J]. Journal of Sound and Vibration, 2018, 423: 17-32. DOI: 10.1016/ j.jsv.2018.06.025.

[24] TAN Xiao-ming, XIE Peng-peng, YANG Zhi-gang, GAO Jian-yong. Adaptability of turbulence models for pantograph aerodynamic noise simulation [J]. Shock and Vibration, 2019, 2019: 6405809. DOI: 10.1155/2019/6405809.

[25] FFOWCS J E, HAWKING D L. Sound generation by turbulence and surfaces in arbitrary motion [J]．Philosophical Transactions for the Royal Society of London, Series A, Mathematical and Physical Sciences, 1969, 264(1151): 321-342. DOI: 10.1098/rsta.1969.0031.

[26] ROSSITER J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds [R]. Farnborough: Royal Aircraft Establishment, 1964. http://resolver.tudelft.nl/uuid:a38f3704-18d9-4ac8-a204-14ae03d84d8c.

[27] ROCKWELL D, NAUDASCHER E. Self-sustaining oscillations of flow past cavities [J]. Journal of Fluids Engineering, 1978, 100(2): 152-165. DOI: 10.1115/ 1.3448624.

[28] YATES J. Interaction with and production of sound by vortex flows [C]// 4th Aeroacoustics Conference. Atlanta, GA, USA AIAA Meeting Paper, 1977: 1-80. DOI: 10.2514/6.1977- 1352.

[29] INAGAKI M, MURATA O, KONDOH T. Numerical prediction of fluid-resonant oscillation at low mach number [J]. AIAA Journal, 2002, 40(9): 1823-1829. DOI: 10.2514/ 2.1859.

[30] LIU Hong-kang, YAN Chao, ZHAO Ya-tian, QIN Yu-pei. Analysis of pressure fluctuation in transonic cavity flows using modal decomposition [J]. Aerospace Science and Technology, 2018, 77: 819-835. DOI: 10.1016/j.ast.2018. 03.033.

(Edited by FANG Jing-hua)

中文导读

高速列车头车1位转向架区域的空气动力噪声特性

摘要：本文采用大涡模拟和FW-H声学类比的仿真方法对高速列车头车1位转向架气动发声主尺度进行了分析，获得了该区域气动噪声的发声机理。流场气动激励结果表明，转向架将转向架腔分隔为两个腔体，每个腔体内都形成了较大的环流，其流场脉动频谱呈现多峰离散特性。远场噪声结果表明，在55.56~97.22 m/s的速度范围内，转向架区域的气动发声机理是相似的。空腔噪声是高速列车头车1位转向架区域的主要噪声机制，转向架的存在将转向架腔分成两个腔体，改变了该腔的发声模式。

关键词：大涡模拟；高速列车；流场结构；气动噪声；转向架

Foundation item: Project(2017YFB1201103) supported by the National Key Research and Development Plan of China; Project(2019zzts540) supported by the Graduate Student Independent Innovation Project of Central South University, China

Received date: 2019-09-09; Accepted date: 2020-03-04

Corresponding author: TAN Xiao-ming, PhD, Lecturer; Tel: +86-15274972406; E-mail: tanxiaoming_csu@163.com; ORCID: 0000- 0001-5096-931X