广义压电动态
积分的守恒性及其应用
黄尚安1, 刘志久1, 刘文胜2, 杨 慧3, 黎振兹1
(1. 中南大学 土木建筑学院, 湖南 长沙, 410083;
2. 中南大学 粉末冶金国家重点实验室, 湖南 长沙, 410083;
3. 中南大学 资源与安全工程学院, 湖南 长沙, 410083)
摘要: 在裂纹绝缘与应力自由的条件下, 证明了考虑压电效应与惯性效应的广义压电动态
积分与围道Γ的选择无关, 这一特性称为广义压电动态积分的守恒性。 若所有电场量为零, 广义压电动态积分变为断裂动力学中的J积分。 在线弹性情况下, 导出了压电动态积分与
的关系。 以压电陶瓷(BaTiO3)板中央有限裂纹对入射反平面剪切谐波的散射为例, 给出了规范化动应力强度因子
随规范化圆频率
的变化曲线。 研究结果表明: 在该曲线上存在峰值与谷值; 当
时, 
, 该峰值比其相应的静态值高27%, 因此, 惯性效应不能忽略; 当
时,
; 当
时, 
, 即动应力强度因子趋近于相应的静态值。
关键词: 动态积分; 守恒性; 反平面剪切波散射; 动应力强度因子
中图分类号:O346.1 文献标识码:A 文章编号: 1672-7207(2005)06-1084-05
The independent of the generalized piezoelectric
dynamic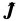 
integral and its application
HUANG Shang-an1, LIU Zhi-jiu1, LIU Wen-sheng2, YANG Hui3, LI Zhen-zi1
(1. School of Civil and Architectural Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;
3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: The generalized piezoelectric dynamic integral including piezoelectric and inertia effects is unaffected by the selection of contour, if the conditions σinnj=0, Djnj=0 are satisfied on the surface of the crack. Therefore, the generalized piezoelectric dynamic integral equation can be called the path-independent of the generalized piezoelectric dynamic integral of the contour Γ. If all the electrical field quantities are made to vanish, then equation (1) reduces to the dynamic J-integral of fracture mechanics. For example, the scattering of an incident anti-plane shear wave by a finite crack in an infinite piezoelectric ceramics (BaTiO3) plate is studied. The curve of variation of normalized DSIF
against normalized circular frequencyis plotted. The results show that the curve of variation of against has peak value and minimum value. As, . This peak value 
is about 27% larger than corresponding static value. Therefore, inertia effect cannot be omitted. As, . As , . This is to say, the mode-Ⅲ dynamic stress intensity factor approaches to corresponding static value.
Key words: dynamic-integral; conservation; scattering of anti-plane shear wave; dynamic stress intensity factor
在一般压电陶瓷介质中, 难以得到动态裂纹问题的电弹性解析解[1-5]。 在裂纹表面绝缘和应力自由的条件下, 许多研究者对压电静态J积分及其守恒性进行了研究, 如: J.D.Eshelby[6]定义了压电静态J积分; Y.E.Pak等[7]从能量守恒定律出发, 研究了压电介质静态J积分及其守恒性, 并运用交替直接方法与发散量定理[8], 取电焓密度代替拉格朗日密度, 讨论了一般压电陶瓷介质的静态J积分及其守恒性。 此后, J.Z.Zuo等[9]对压电静态J积分及其守恒性也进行了讨论。 上述研究仅限于研究在静态条件下压电J积分的定义及其路径无关性。 然而, 对于动荷载(包括弹性波)作用下的稳定裂纹问题, 载荷的加载速率将引起惯性效应。 Y.Shindo等[10-12]研究了裂纹没有扩展, 同时考虑压电效应与惯性效应的压电动态积分。 目前, 尚没见从理论上证明广义压电动态积分与路径无关的报道。 在此, 本文作者在裂纹绝缘和应力自由的条件下, 证明广义压电动态积分与围道Γ的选择无关。 这一特性称为广义压电动态积分的路径无关性。积分目前主要用于动态裂纹初始问题的数值分析。 应当指出的是, 若所有电场量为零, 则广义压电动态积分可变为断裂力学中的J积分[13-14]。
1 压电动态积分的守恒性
Y.E.Pak[7]从能量守恒定律出发分析压电介质平面问题, 定义广义压电动态积分(见图1)为:
式中: Ω为围道Γ所包围的面积; 电焓密度H=W-EjDj; W为压电介质的内能密度; εij为应变张量; Ej为电场强度分量; Dj为电位移分量; 围道Γ上作用有应力分量
; σij为应力张量; nj为面元处单位外法线矢量的分量; ds为弧长。 这里采用张量求和的写法。
若围道已经选定, 广义压电动态积分便为一定值。 这里将证明, 只要下列3个条件满足:
a. 电弹性状态与坐标x3(z)无关; 水平放置的裂纹(或切口)表面是绝缘的, 而且是应力自由的;
b. 裂纹没有扩展, 仅仅是所受的动态机电荷载(包括弹性波)随时间迅速变化;
c. 围道都是从裂纹下侧的水平部分出发, 直到裂纹上侧的水平部分为止, 如图1中的A′B′或AB。
此时, (1)式所示的广义压电动态积分和路径无关, 这叫做广义压电动态积分的路径无关性。
图 1 围绕裂纹顶端的积分围道
Fig. 1 Surrounding of integration bounding the crack tip
设考虑2个任意包围裂纹顶端的路径Γ与Γ′, 分别用1与2代表相应的压电动态积分值, 则有
再设Γ*为任一闭曲线(图1), 它的内部无被积函数的奇异性; Ω*为Γ*包围的面积, 此时, 有
式中: Γ*=Γ+Γs-Γ′-Γ′s; Ω*=Ω-Ω′; Γs与Γ′s分别为相应闭路在裂纹面的部分。 且在Γs与Γ′s上, 有
σijnj=0, Djnj=0。(4)
运用Gauss定理与运动方程σij,j=ρüj, 并据
H,1=σijεij,1-DjEj,1, DjEj,1=DjE1,j,(5)
得:
将式(6)代入式(3), 得:
1-2=0。(7)
从而证明了压电介质广义动态积分值与路径无关。
应当强调指出, 在上面证明过程中, 对压电材料性质没有特殊要求, 因而广义压电动态积分式(1)既适用于线性弹性, 也适用于非线性弹性压电材料。
2 广义压电动态积分与的关系
上面证明了广义压电动态积分的路径无关性, 下面讨论这个量的物理意义。 在此, 以Ⅲ型纹受反平面冲击荷载为例, 首先证明, 在线性弹性情况下, 有:
计算下列定积分:
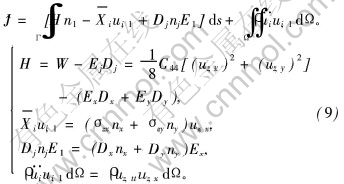
积分路径Γ是以裂纹端为圆心, 半径为r的圆(见图2), 故有
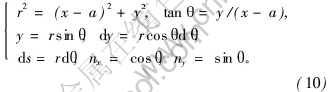
裂纹前端邻近区域电弹性动态场公式为
图 2 计算动态积分的圆形围道
Fig. 2 Circular contour of calculating dynamic integration
注意到:
展开(1)式, 得:
将式(10), (11)与(12)代入式(13), 并经化简整理后, 得:
考虑到:
于是, 有
由此可见, 在线弹性状态下, 广义压电动态积分通过式(16)决定裂纹前端区域场的强度。
因此, 若利用上述等式和任意一种方法(包括有限元法)解算出任意围道上广义压电动态积分值, 便可以算出动应力强度因子。 此积分围道通常选择在离裂纹端一定距离处。 用直接分析裂纹端电弹性场的方法决定值时, 必须确定裂纹端的奇异性。 但在远离裂纹端的围道上, 已无应力的奇异性, 此时, 压电动态积分的计算即通常的定积分计算, 可以代替应力场奇异性的计算, 从而保证了计算结果的精确性。
3 实 例
21世纪以来, 分析压电介质中裂纹对弹性波的散射[11-12]是国内外研究者极为关注的问题之一。 这里采用绝缘裂纹假设, 讨论无限压电陶瓷板内有限裂纹对入射反平面剪切谐波的散射问题, 利用广义压电动态积分的定义式, 获得压电陶瓷板(材料BaTiO3)内裂纹尖端处III型动应力强度因子的数值解。
设沿z轴方向的SH型入射波是平面剪切谐波:
式中: u0为波幅; γ3为入射角(γ3=90°); 
为波数; ω为圆频率; c为剪切波速。
当入射SH波作用于裂纹时, 应力状态属于断裂力学意义上的Ⅲ型问题。 u(t)x=u(t)y=0, 非零位移仅有1个, 即u(t)z。 其中上标t表示总位移场, 它由入射波场u(i)z与散射波场uz所组成, 即
u(t)z(x,y,t)=u(i)z(x,y,t)+uz(x,y,t)。(18)
其中, 入射波场已知, 自动满足控制方程(不计体力与体电荷密度):
其中:
ρ为质量密度; C44, e15与d11分别为压电材料的弹性模量、 压电常数与介电常数; uz为平面外位移; φ为与电势有关的函数。
散射波场uz待定, 它是方程组(19)在一定边界条件下的解。 首先, 它要满足无限远处的边界条件:
由于考虑的裂纹位于无限压电平面的正中央, 因此, 应满足下列边界条件:
散射场的边界条件为
σyz(x,0,t)=-τ0H(t), 0≤x〈a, t>0;
Ex(x,0,t)=Ecx(x,0,t),
Dy(x,0,t)=Dcy(x,0,t), 0≤x〈a, t>0。(23)
式中: 
; 上标c代表沿裂纹内部自由空间产生的电量。
动应力强度因子与广义压电动态积分有如下关系:
因此, 对于反平面情况, 通过计算积分(式(1))可以确定。 计算积分值, 可用有限元法先求出裂纹前端邻近区域内各应力分量、 应变分量、 位移分量、 电位移分量, 电场强度分量的数值解。 根据这些数值解, 便可以计算围绕裂纹前端的任一积分线路Γ的积分。 由于积分的路径无关性, 积分的数值与所选积分回路无关, 因此, 可以避开裂纹前端场急剧变化的微小区域, 从而保证计算结果的精确性。
已知压电材料常数[15]: 弹性常数C44=4.4×1010N/m2, 压电常数e15=11.4C/m2, 介电常数d11=128.3×10-10C/m, 质量密度ρ=5.7×103kg/m3, 剪切波速c=3.167×103m/s。
数值计算结果见图3。 可见, 当与3时,
的变化曲线上存在峰值和谷值, 其最大值与最小值分别为: , 。 该峰值比其相应的静态值高27%。 因此, 惯性效应不能忽略。 此外, 当时, , 即动应力强度因子趋近于相应的静态值。
图 3 规范化动应力强度因子随规范化圆频率的变化
Fig. 3 Normalized dynamic SIFversus normalized circular frequency
4 结 论
a. 广义压电动态积分是一个定义明确, 理论上较严密的电弹性场量。
b. 广义压电动态积分的一个重要特性是它的路径无关性。 在裂纹表面绝缘和应力自由的情况下, 证明了同时考虑惯性效应与压电效应的广义压电动态积分与路径无关。
c. 对于线弹性压电介质, 通过计算积分, 获得了积分与Ⅲ型动应力强度因子之间的关系表达式。
d. 压电介质动态积分能避开直接计算裂纹尖端的电弹性场, 只需应用有限元法近似计算出远离裂尖任一围道Γ上的积分值, 根据式(24)便可求得动应力强度因子。 在远离裂纹端的围道上, 无电弹性场的奇异性, 从而保证了计算结果的可靠性和精确性。
e. 结合压电陶瓷板(材料BaTiO3)内裂纹对入射反平面剪切谐波的散射, 通过数值计算广义压电动态积分, 研究了无因次动应力强度因子的数值结果, 给出了与无因次圆频率的变化关系。 结果表明, 与关系曲线上存在峰值与谷值, , ; 该峰值比其相应的静态值高27%, 由此可知, 惯性效应不能忽略。 当时, , 即Ⅲ型动应力强度因子趋近于相应的静态值。
参考文献:
[1]CHEN Zeng-tao. YU Shou-wen. Crack tip fields of piezoelectric materials under anti-plane impact[J]. Chinese Science Bulletin, 1997, 42: 1613-1619.
[2]CHEN Zeng-tao. Crack-tip fields of an infinite piezoelectric strip under anti-plane impact[J]. Mechanics Research Communications, 1998, 25: 313-319.
[3]CHEN Zeng-tao, YU Shou-wen. A semi-infinite crack under anti-plane mechanical impact in piezoelectric materials[J]. Int J of Fract, 1998, 88: L53-L56.
[4]Kwon J H, Lee K Y, Kwon S M. Moving crack in a piezoelectric ceramic strip under anti-plane shear loading[J]. Mechanics Research Communications, 2000, 27(3): 327-332.
[5]DING Hao-jing, WANG Hui-ming, LING Dao-sheng. Analytical solution of a pyroelectric hollow cylinder for piezothmoelastic axisymmetric dynamic problems[J]. J of Thermal Stresses, 2003, 26(3): 261-276.
[6]Eshelby J D. Energy relations and the energy-momentum tensor in continuum mechanics[M]. New York: MeGraw-Hill, 1970.
[7]Pak Y E, Herrmann G. Conservation laws and the material momentum tensor for the elastic dielectric[J]. Int J Eng Sci, 1986, 24: 1365-1374.
[8]Park Y E. Crack extension force in a piezoelectric material[J]. Trans ASME J Appl Mech, 1990, 57(4): 647-653.
[9]Zuo J Z, Sih G C. Energy density formulation and interpretation of cracking behavior for piezoelectric ceramics[J]. Theoret Appl Fract Mech, 2000, 34(1): 17-33.
[10]Shindo Y, Narita F. Diffraction of an antiplane shear wave by a finite crack in an orthotropic piezoelectric ceramic[J]. Proceedings of Engineering Mechanics, 1995, 1: 577-580.
[11]Narita F, Shindo Y. Scattering of anti-plane shear waves by a finite crack in piezoelectric lamination[J]. Acta Mech, 1999, 134: 27-43.
[12]ZHOU Zhen-gong, LI Hai-chen. Investigation of the Scattering of anti-plane Shear waves by two collinear cracks in a piezoelectric materials using a new method[J]. Acta Mechanics, 2001, 147(1-4): 87-97.
[13]范天佑. 断裂动力学引论[M]. 北京: 北京理工大学出版社, 1990.
FAN Tian-you. Introduction of Fracture Dynamics[M]. Beijing: Beijing University of Science and Technology Press, 1990.
[14]黎振兹. 工程断裂力学基础[M]. 长沙: 中南工业大学出版社, 1990.
LI Zhen-zi. Elementary Engineering Fracture Mechanics[M]. Changsha: Central South University of Technology Press, 1990.
[15]WANG Xu-yue, YU Shou-wen. Transient response of a crack in piezoelectric strip subjected to the mechanical and electrical impacts: made-Ⅲ problem[J]. Int J of Solids and Structures, 2000, 37: 5795-5808.
收稿日期:2005-02-10
基金项目: 国家自然科学基金资助项目(10272043)
作者简介: 黄尚安(1949-), 男, 湖南宁远人, 教授, 博士, 从事断裂力学研究
论文联系人: 黄尚安, 男, 教授, 博士; 电话: 13808424967(手机); E-mail: h3an2008@yahoo.com.cn
