J. Cent. South Univ. Technol. (2011) 18: 809-815
DOI: 10.1007/s11771-011-0766-7
Super-resolution reconstruction of synthetic-aperture radar image using adaptive-threshold singular value decomposition technique
ZHU Zheng-wei(朱正为)1, 2, ZHOU Jian-jiang(周建江)1
1. College of Information Science and Technology, Nanjing University of Aeronautics and Astronautics,
Nanjing 210016, China;
2. School of Information Engineering, Southwest University of Science and Technology, Mianyang 621010, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A super-resolution reconstruction approach of radar image using an adaptive-threshold singular value decomposition (SVD) technique was presented, and its performance was analyzed, compared and assessed detailedly. First, radar imaging model and super-resolution reconstruction mechanism were outlined. Then, the adaptive-threshold SVD super-resolution algorithm, and its two key aspects, namely the determination method of point spread function (PSF) matrix T and the selection scheme of singular value threshold, were presented. Finally, the super-resolution algorithm was demonstrated successfully using the measured synthetic-aperture radar (SAR) images, and a Monte Carlo assessment was carried out to evaluate the performance of the algorithm by using the input/output signal-to-noise ratio (SNR). Five versions of SVD algorithms, namely 1) using all singular values, 2) using the top 80% singular values, 3) using the top 50% singular values, 4) using the top 20% singular values and 5) using singular values s such that s2≥max(s2)/rinSNR were tested. The experimental results indicate that when the singular value threshold is set as smax/(rinSNR)1/2, the super-resolution algorithm provides a good compromise between too much noise and too much bias and has good reconstruction results.
Key words: synthetic-aperture radar; image reconstruction; super-resolution; singular value decomposition; adaptive-threshold
1 Introduction
The higher the radar image resolution is and the better the quality is, the more the target information we can obtain from the image will be and the better the subsequent application (for example, automatic target recognition) performance will be [1]. So, it is of important application values to study the radar image resolution promotion techniques.
We can improve the radar image resolution by two ways [2]: 1) improving the theoretical resolution of a radar system by ameliorating or updating the system hardware; 2) improving the accuracy of various algorithms using soft data processing techniques. Super- resolution is a technique which improves the resolution of radar images (beyond the theoretical system resolution limit) by various signal processing techniques and knowledges about radar point spread function (PSF), target scene, noise power and so on [2-3]. At present, the super-resolution techniques used in radar image quality improvement mainly include the Bayesian approach [4], matrix pseudo- inverse (PINV) algorithm [5], minimum mean-square error (MMSE) algorithm [6], multiple signal classification (MUSIC) algorithm [7-8] and singular value decomposition (SVD) algorithm [9-11].
The Bayesian solution differs from the other algorithms. Rather than estimating a single value for original scene, the probability density for many values of original scene is estimated and a series of samples are produced to characterize the probability density function [4]. The PINV algorithm is a benchmark solution with which other super-resolution algorithms should be compared. It is a well-known least-square procedure for solving the systems of linear equations. However, the super-resolution performance of the algorithm is usually poor due to the ill-conditioned nature of the problem, that is, a large number of spurious scatterers are often placed at the positions where there is no valid target [5]. The MMSE algorithm is a similar approach to the least squares. The object of the approach is to choose the linear reconstruction operator R, such that the super- resolution solution given by fr=Rg minimizes the expected norm J=á|| fr-f ||2? (where f is the original target scene) of the reconstruction error. However, in practice, f is not known in advance because prior knowledge of the scene is not well defined. Therefore, an iterative scheme that estimates f from the measured data must be used [12]. Another disadvantage of the MMSE algorithm is that it requires to know the noise power in advance [6]. Perhaps the most studied super-resolution algorithm, for data measured from an array of receivers, is the MUSIC algorithm [7]. The algorithm models the observed data as the combination of a signal subspace and an orthogonal noise subspace. The number of point sources in a scene is determined by analyzing the eigenvalue spectrum of the measured covariance matrix. The direction of the sources is determined by the position of the strongest peaks in a power function, and then the parameters of the point sources can be calculated. Obviously, the computation complexity of the algorithm is high [7-8]. In the SVD algorithm, the PSF matrix is decomposed into three matrices: two orthogonal matrices and a diagonal matrix with singular values on the diagonal [9-11]. Any singular value below a certain threshold is set to zero and the effective inverse of the PSF matrix is calculated with special properties of the three matrices where the inverse of zeroed singular values is set to be zero. If all the original singular values are retained, then the algorithm is equivalent to the PINV algorithm. The removal of several small singular values, which are responsible for the amplification of noise, results in a better performance than the PINV algorithm. But, the singular-value threshold level for the algorithm is not defined in the literatures.
In this work, a radar image super-resolution reconstruction approach using an adaptive-threshold SVD technique was presented, and its two key aspects, namely the determination method of PSF and the selection scheme of singular-value threshold, were given.
2 Outline of imaging model and super- resolution reconstruction
Assume that each radar target has a high-resolution two-dimensional plan-view back-scattering coefficient or distributed radar cross section (RCS), which is a function of imaging geometry. When being imaged by a coherent radar, the RCS gives rise to a complex scattered field. The formation process of the image is equivalent to the convolution of the PSF of the radar system and the high-resolution complex representation of the target scene. The imaging process may be mathematically described by [13]
g=Tf+n (1)
where f is a complex vector denoting the original high-resolution target scene, in which surrounding clutter is implicitly included; T is an appropriately formatted Toeplitz convolution matrix that reflects the effect of the PSF; the thermal noise in the radar receiver is modeled by n; g is a complex vector representing the resultant low-resolution image.
The estimation of the original scene f, given the measured image g and noise n, is a super-resolution reconstruction problem.
3 Adaptive-threshold SVD super-resolution
3.1 Basic SVD algorithm
In the SVD algorithm, the PSF matrix T is decomposed into three matrices:
T=USVH (2)
where U and V are orthogonal matrices, S is a diagonal matrix whose elements comprise singular values si, and H denotes the complex-conjugate transposed operator (Hermitian).
Any singular value in S below a given threshold is set to be zero and the inverse of the new matrix is calculated as
(3)
where the inverse of the zero values in Sth are also set to be zero. Thus, the SVD solution is given by
(4)
The removal of several small singular values, which are responsible for the amplification of noise, results in the estimated scenes with a higher SNR than the PINV algorithm. If all the singular values are retained, then the SVD algorithm would be equivalent to the PINV algorithm [9]. In fact, the condition number of a matrix is equal to the ratio of the largest to the smallest singular value, so it would be expected that the algorithm should show an improvement over the PINV algorithm. However, it should also be noted not to remove too many singular values because each column of U or V corresponds to a specific structure in T. When a singular value is set to be zero, the output matrix Tsvd would miss that structure from the scene estimation and it would result in a biased estimation. The threshold level for singular values is not defined in the basic algorithm. But, in the later testing of the algorithm using the measured radar data, it is found that removing singular values si which is below a threshold of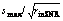 
(where smax is the largest singular value in the diagonal matrix S and rinSNR is the signal-to-noise ratio (SNR) of the input image) provides a good compromise between too much noise and too much bias.
From the above discussion, we can see that, the two key problems in the SVD super-resolution algorithm are the determination of PSF matrix T and the selection of singular-value threshold, which will directly impact on the quality of super-resolved images.
3.2 Determination of PSF
The super-resolution reconstruction problem of the measured image is an inverse problem of the imaging process. It requires the use of prior knowledge about radar PSF, whose accuracy will directly impact on the quality of the super-resolved reconstruction scene. The PSF may be estimated using the knowledge of signal bandwidth. Once the radar is built, the PSF might also be measured by recording the data from a strong point scatterer such as a trihedral reflector. However, many factors will lead to the change of radar PSF, so the PSF should be determined according to the specific application. In general, the precise nature of the radar PSF depends on aircraft and radar parameters. In a typical case, the relevant parameters are: the minimum range, R0=40 km; the radar wavelength, λ=0.03 m; the radar antenna length, d=2 m; the aircraft velocity, vx= 200 m/s; the synthetic-aperture time, T=3 s.
For a sideways looking radar traveling in a straight line, the range-to-target is given by
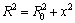(5)
where x is the distance traveled by the radar platform from the position of closest approach. Since x<0, it may be approximated by
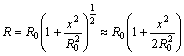(6)
The amount that the range-to-target differs from the minimum range is then given by
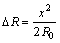(7)
If the radar platform undergoes constant cross-track acceleration ay, there is an additional displacement of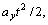 
where t is the time elapsed with the closest approach. Thus, the overall variation in phase with time is
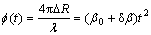(8)
where λ is the radar wavelength;
(9)
For the sake of simplicity, we mark
(10)
The signal received by the radar for a point target is s(t)=exp(-if(t)) and the output of matched filter is given by the cross-correlation of this with a reference signal h*(t)=exp(iβ0t2):
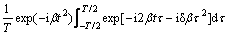(11)
where τ is the integral variable.
If the cross-track acceleration δβ is equal to zero, then Eq.(11) may be simplified to the familiar modulated Singh function:
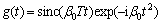
or else the integral in the final equation of Eq.(11) can be Fourier transformed into
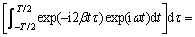
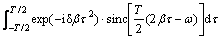(12)
where ω represents the frequency.
If π/βT<<1 (which holds well for the parameters used here), the width of the sinc function in Eq.(12) would be much less than its height, so it may be approximated by a Dirac delta function:
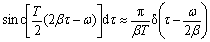(13)
Using this approximation gives the Fourier domain representation of the integral as
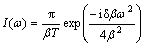(14)
The inverse Fourier transform of this function cannot be evaluated in terms of simple functions. However, the analytical form when using integration limits ω=±W/2 is given as
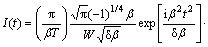
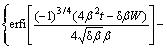
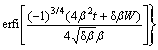(15)
where erfi(z)=erf(iz)/i and erf(z)=
Eq.(15) can be substituted for the integral in Eq.(11) to give the desired PSF as a function of time:
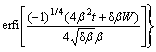(16)
To obtain the PSF in spatial co-ordinates, t, δβ and β
are just replaced with x/vx, 2πay/λ and 
respectively.
3.3 Selection of singular value threshold
Just as mentioned above, the noise can be reduced and the SNR of the estimated scene can be increased by removing several small singular values in the matrix S. But, if too many singular values are removed, the output matrix Tsvd would miss the structure from the scene estimation and this would result in a biased estimation. Therefore, selection of the threshold level is very important, which will directly affect the result and performance of the SVD super-resolution. To solve the problem, five versions of SVD algorithms in which different thresholds were used to determine the number of singular values were tested: 1) all singular values were used in the calculation; 2) the top 80% singular values were used; 3) the top 50% singular values were used; 4) the top 20% singular values were used; 5) singular values of s such that s2≥max(s2)/rinSNR were used. The experiment indicated that the best performing algorithm is the one based on the adaptive threshold, namely the fifth algorithm. It provides a good compromise between too much noise and too much bias and has a good super-resolution result.
4 Results and discussion
4.1 Markov chain Monte Carlo algorithm
The Markov chain Monte Carlo (MCMC) is a popular class of algorithms to sample from a complex distribution. MCMC algorithms provide a general framework for generating samples Xt from a complicated target probability distribution P(?) that cannot be sampled with simple distribution-specific methods [14]. MCMC does not sample directly from P(?) but only requires that the density P(X) can be evaluated within a multiplicative constant P(X)=P′(X)/Z, where Z is a normalization constant and P′(?) is the unnormalized target distribution. A Markov chain is a discrete-time stochastic process {X0, X1, …} with the property that the state Xt given by all previous values {X0, X1, …, Xt-1} only depends on Xt-1: P(Xt|X0, X1, …, Xt-1)=P(Xt|Xt-1). We call P(?|?) the transition matrix of the Markov chain. P(?|?) is a stationary (this is, independent of time t) transition matrix with the following properties: 1) all the entries are non-negative, and 2) the sum of the entries in a row is 1. We assume that P(?)>0. MCMC converges, in infinite time, to the probability distribution P(·), thus it samples with higher probability from more important states of P(·).
The particular algorithm used in this experiment is a Metropolis-Hastings (M-H) algorithm [15]. Since we cannot sample directly from P(?), the M-H algorithm considers a simpler distribution S(?|?), called the proposal distribution for sampling the next state of a MCMC chain. S(Xnew|Xt) generates the candidate state Xnew from the current state Xt, and the new state Xnew is accepted with a probability:
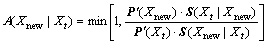(17)
If the candidate state is accepted, the next state becomes Xt+1=Xnew; otherwise, Xt+1=Xt. The transition probability for arriving in Xnew when the current state is Xt is T(Xnew|Xt)=S(Xnew|Xt)·A(Xnew|Xt), if Xnew≠Xt, and
otherwise T(Xnew|Xt)=1-
More details about the contents of the MCMC algorithm and the M-H algorithm may be found in Refs.[14-15].
4.2 Super-resolution performance measurement
According to the imaging model, the SNR of the input image g (namely the input signal-to-noise power ratio) may be defined as
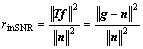(18)
where n denotes the thermal noise.
If the estimated scene obtained by a certain super- resolution algorithm is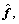 
then the SNR of the output image (namely the reconstruction scene) may be defined as
(19)
Obviously, it is possible to calculate this parameter only when the true scene f is known.
The above-mentioned input/output SNR will be adopted to measure the super-resolution performance of the SVD and other algorithms.
4.3 SVD reconstruction results and performance
A 41×41 pixel image of a T-72 tank taken from the MSTAR SAR data set was taken as the high-resolution scene f. The original high-resolution scene and degraded low-resolution images are shown in Fig.1. In the reconstruction experiment, the noise was added to the low-resolution image with SNR ranging from 0 dB to 50 dB. At each SNR, ten images were generated with different noise realizations. The SVD algorithm was applied, and the mean output SNR was measured. Five versions of SVD algorithms were tested, in which a different threshold was used to determine the number of singular values. They were: 1) all singular values in the calculation, 2) the top 80% singular values, 3) the top 50% singular values, 4) the top 20% singular values, and 5) singular values of s such that s2≥max(s2)rinSNR.
Fig.1 Test images: (a) Original high-resolution image; (b) Low- resolution image
The singular value spectrum of the 1 681×1 681 convolution matrix is shown in Fig.2. It can be seen that the smallest value has a very low magnitude compared with the largest value. The results of all the SVD super-resolution algorithms, except for the all-singular-value version, are shown in Fig.3. From Fig.3, we can see that the best performing algorithm is the one in which an adaptive singular-value threshold is used, namely the algorithm in which singular value s≥ 
is used. It is the only version to maintain an output SNR greater than 0 dB for the whole range of input SNRs, and it provides a good compromise between too much noise and too much bias. At low SNRs, the majority of the singular values are excluded, which tends to produce images that are not fully super-resolved but do not contain any spurious noise spikes. At higher SNRs, more singular values are used, which allows a more accurate super-resolution result. The next best performing version is the one in which the top 20% singular values are used. At low SNRs, more singular values are used than the adaptive threshold version. Using too many singular values allows the creation of noise spikes, which explains the lower performance of this algorithm at low SNRs. At high SNRs tested, the algorithm uses a similar number of singular values as the adaptive threshold version and has a similar performance. Ultimately, when the SNR approaches infinity, more than 20% of the singular values should be used and the performance of this version would be expected to be lower than the adaptive threshold version of the algorithm. For the other versions of SVD algorithms that use a fixed percentage of singular values, similar comments to those made for the 20% version may be obtained, except that they clearly use too many values for the range of SNRs tested. The performance of the algorithm that uses all singular values is not shown in Fig.3 as its output SNR is constantly about 100 dB below that of 80% version.
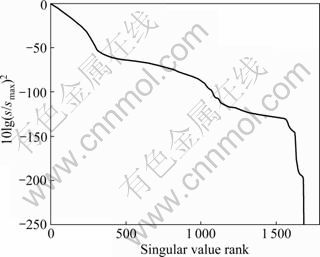
Fig.2 Singular value spectrum of convolution matrix
Fig.3 Performance of four versions of SVD algorithms
The original and super-resolved scenes for the adaptive-threshold SVD algorithm at an input SNR of 30 dB are shown in Fig.4. Although the output SNR of the super-resolved scene is only about 5 dB, the algorithm has visually done a reasonable job of restoring the scene from the low-resolution image shown in Fig.1(b), and the overall objective shape and location of strong scatterers have been correctly reconstructed. SNR of 5 dB may seem low, but it should be remembered that it is a mean-signal to mean-noise power ratio based on the whole image rather than the peak SNR used in target detection, which is always higher. The resolution of the super-resolved scene is slightly lower than the original one, and it can be seen that a little detail of the original scene has been lost in the super-resolved scene. Given that in the adaptive-threshold version of the SVD algorithm, SNR is taken into account, it seems like a good candidate for a general super-resolution algorithm.
Fig.4 Original and super-resolved scenes: (a) Original scene; (b) SVD super-resolved scene
4.4 Performance comparison
For comparison, the performances of several other algorithms were also measured. Each algorithm was applied using the same input image with the input SNR varying from 0 to 50 dB. Ten Monte Carlo runs for each value of the input SNR were used and the output SNR was calculated for each run. The results are shown in Fig.5(a). It is immediately evident from Fig.5(a) that the algorithms provide a trade-off between the resolution and the SNR. Although the resolution has improved, it is at the expense of a loss in SNR. At high input SNRs, the performance of all the algorithms begins to converge. However, at low SNRs, the SVD algorithm performs best. In general, the output SNR seems low due to an inadequacy of the metric as a performance measure. If a strong scatterer is present and its amplitude is correctly estimated but its position is incorrect by one pixel, then it appears to be a strong noise spike, which degrades the SNR. However, by visually examining the recovered field solution in Fig.4, the major features of the target are still present. Therefore, a feature-based automatic target recognition (ATR) system should still have a reasonable performance even with a low apparent SNR. The results displayed in Fig.5(a) are based on the situation where there is perfect knowledge of the PSF. In practice, this is unlikely to be the case because there will be some residual error in the autofocus procedure. The effect of this has been modeled by reducing the level of defocus that the algorithms assume by half, while actually applying the original level of defocus (by assuming defocus level δβ=0.005 and true defocus level δβ=0.010). The results are shown in Fig.5(b). There is a little change in performance at low SNRs because the noise dominates any error in the PSF. However, as the SNR increases, the effect of an incorrect PSF is apparent, that is, it puts a limit on the output performance whatever the input SNR is. If a parametric model of the PSF distortion is available, then this performance loss could be mitigated by estimating the parameters of the model [4, 16].
Fig.5 Performance of super-resolution algorithms: (a) Correct PSF; (b) Modified PSF
It has been shown that the super-resolution can aid automatic target recognition, but the super-resolution performance assessment based on the output SNR may not necessarily capture the effects of super-resolution on the target feature values. So, it is a subject worthy of further research that the super-resolution algorithms are incorporated into an automatic target recognition system and are assessed based on classification performance.
5 Conclusions
1) The adaptive-threshold SVD algorithm is the best performing one in the five versions of SVD algorithms, and it provides a good compromise between too much noise and too much bias. At low SNRs, the majority of singular values is excluded, which tends to produce the images that are not fully super-resolved but do not contain any spurious noise spikes. At higher SNRs, more singular values are used, which allows a more accurate super-resolution result.
2) Comparing the super-resolved scene with the low-resolution image and the original scene, we can see that the adaptive-threshold SVD algorithm does a reasonable job of restoring the scene from the low- resolution image, and the overall objective shape and location of strong scatterers are correctly reconstructed.
3) Compared with the other algorithms, the adaptive-threshold SVD algorithm performs best at low SNRs and the performance of all the algorithms begins to converge at high input SNRs.
4) Just as other super-resolution algorithms, the adaptive-threshold SVD algorithm improves the resolution at the expense of a loss in SNR and is sensitive to the accurate knowledge of the PSF.
Acknowledgements
The authors would like to thank Dr. R. O. Lane for his kind help and support in the accomplishment of this paper.
References
[1] ZHU Zheng-wei, ZHOU Jian-jiang. Optimum selection of common master image for ground deformation monitoring based on PS-DInSAR technique [J]. Journal of Systems Engineering and Electronics, 2009, 20(6): 1213-1220.
[2] WANG Zheng-ming, ZHU Ju-bo. SAR image resolution improvement technology [M]. 1st ed. Beijing: Science Press, 2006: 1-9. (in Chinese)
[3] SULLIVAN R J. Radar foundations for imaging and advanced concepts [M]. 1st ed. Raleigh: SciTech Publishing Inc, 2004: 155-169.
[4] LANE R O, COPSEY K D, WEBB A R. A Bayesian approach to simultaneous autofocus and super-resolution [C]// Proceedings of SPIE. Denver: SPIE Press, 2004: 133-142.
[5] SAMSONOV A, BLOCK W F, FIELD A S. Reconstruction of MRI data using sparse matrix inverses [C]// The Forty-First Asilomar Conference on Signals, Systems and Computers. Pacific Grove: IEEE Press, 2007: 1884-1887.
[6] SEL?N Y, STOICA P. Estimation of semi-sparse radar range profiles [J]. Digital Signal Processing, 2008, 18(4): 543-560.
[7] KIM K T, SEO D K, AND KIM H T. Efficient radar target recognition using the MUSIC algorithm and invariant features [J]. IEEE Transactions on Antennas and Propagation, 2002, 50(3): 325-337.
[8] THOMPSON P, NANNINI M, SCHEIBER R. Target separation in SAR image with the MUSIC algorithm [C]// IEEE International Geoscience and Remote Sensing Symposium, Barcelona: IEEE Press, 2007: 468-471.
[9] LANE R O, COPSEY K D, WEBB A R. Assessment of a Bayesian approach to recognizing relocatable targets [C]// NATO RTO SET-096 Specialists’ Meeting on the Millimeterwave Advanced Target Recognition and Identification Experiment. Oberammergau: IEEE Press, 2005: 1-12.
[10] RODRIGUEZ J L, TABOADA J M, ARAUJO M G, OBELLEIRO BASTEIRO F, LANDESA L, GARCIA TUNON J I. On the use of the singular value decomposition in the fast multipole method [J]. IEEE Transactions on Antennas and Propagation, 2008, 56(8): 2325-2344.
[11] ABUJARAD F, NADIM G, OMAR A. Clutter reduction and detection of landmine objects in ground penetrating radar data using singular value decomposition (SVD) [C]// Proceedings of the 3rd International Workshop on Advanced Ground Penetrating Radar. Delft: IEEE Press, 2005: 37-42.
[12] LUTTRELL S P. Prior knowledge and object reconstruction using the best linear estimate technique [J]. Optica Acta, 1985, 32(6): 703-716.
[13] YANG Jie, SARKAR T K. Interpolation/extrapolation of radar cross-section (RCS) data in the frequency domain using the Cauchy method [J]. IEEE Transactions on Antennas and Propagation, 2007, 55(10): 2844-2851.
[14] M?D?LINA M D, DIRK T. Evolutionary Markov chain Monte Carlo [M]. New York: Springer Berlin/Heidelberg, 2004: 63-76.
[15] CHIB S, GREENBERG E. Understanding the Metropolis-Hastings algorithm[J]. The American Statistician, 1995, 49(4): 327-335.
[16] COPSEY K D, LANE R O, WEBB A R. Designing NCTR algorithms when operating sensor conditions differ from training conditions [C]// International Conference on Radar Systems. Toulouse: SPIE Press, 2004: 126-131.
(Edited by YANG Bing)
Foundation item: Project(2008041001) supported by the Academician Foundation of China; Project(N0601-041) supported by the General Armament Department Science Foundation of China
Received date: 2010-01-27; Accepted date: 2010-05-10
Corresponding author: ZHU Zheng-wei, PhD; Tel: +86-816-6957371; E-mail: zhuzwin@163.com
