DOI: 10.11817/j.issn.1672-7207.2016.05.015
基于半监督PCA-LPP流形学习算法的故障降维辨识
张晓涛,唐力伟,王平,邓士杰
(军械工程学院 火炮工程系,河北 石家庄,050003)
摘要:提出一种基于半监督思想PCA-LPP的流形学习维数约简故障辨识方法,兼顾PCA的全局结构和LPP的局部结构保持以及样本的类别信息,构造新的投影矩阵目标函数,给出PCA-LPP流形学习算法的计算原理。采用UCI中wine数据集验证半监督PCA-LPP方法的维数约简性能,并就齿轮箱故障声发射实验信号,以小波包能量熵作为特征向量,并将特征向量的降维结果输入支持向量机进行故障类型辨识。研究结果表明:半监督PCA-LPP方法的降维结果,能够充分考虑不同故障特征向量的差异信息,相应的故障类型辨识精度高于PCA及LPP方法。
关键词:流形学习;局部保持投影;主元分析;故障诊断;故障辨识
中图分类号:TH165;TN911 文献标志码:A 文章编号:1672-7207(2016)05-1559-06
Fault identification and dimensionality reduction method based on semi-supervised PCA-LPP manifold learning algorithm
ZHANG Xiaotao, TANG Liwei, WANG Ping, DENG Shijie
(First Department, Ordnance Engineering College, Shijiazhuang 050003, China)
Abstract: A novel fault identification dimensionality reduction method based on semi-supervised PCA-LPP manifold learning algorithm was proposed. The objective function of projection matrix of semi-supervised PCA-LPP was constructed by global structure and local structure, the global structure was described by PCA, the local structure described by LPP and category information of samples, and the calculation principle of semi-supervised PCA-LPP manifold learning algorithm was given. The processing results of wine dataset of UCI show that the semi-supervised PCA-LPP method has a good ability of dimensionality reduction. Aiming at the gearbox acoustic emission signals, its eigenvectors is constructed by wavelet packet energy entropy, and the dimensionality reduction results of eigenvectors are given to the support vector machine, the fault identification of semi-supervised PCA-LPP method obtains higher identification rate than that of LPP and PCA, because the method considers the similarities and differences between all eigenvectors.
Key words: manifold learning; locality preserving projection; principal component analysis; fault diagnosis; pattern recognition
齿轮箱故障诊断中,原始采样信号由于干扰成分的影响,采样信号提取的初始故障特征往往无法有效进行状态识别和故障诊断[1]。故障特征的提取和降维对故障类型的识别和诊断具有非常重要的意义,然而由齿轮箱转子结构以及工作状态的复杂性,载荷、摩擦等因素所引入的非线性影响[2],传统线性降维方法PCA(principal component analysis,PCA)处理后的故障特征,通过发现特征全局欧式结构,使全局分布方差最大[3],却忽略了数据的局部结构特征,导致PCA处理后的故障特征不同类别之间混叠严重,无法实现良好的故障诊断。流形学习是一类无监督非线性学习算法[4-5],能够有效地提取嵌入在高维数据中的低维特征,为后续故障的分类提供有效的特征降维处理支 持[6]。局部保持投影(locality preserving projection,LPP)是一种典型的流形学习算法,由HE等[7]在拉普拉斯特征映射的基础上提出,局部保持投影在降维过程中能够保持数据样本局部流形结构不变,FADI等[8]将有监督正交LPP用于人脸识别,MAO等[9]将半监督LPP用于文稿语义分类,WONG等[10]将有监督归一化LPP用于车辆数据集分类,DENG等[11]将稀疏核LPP用于非线性过程故障检测,以上有关LPP的研究在数据降维和分类中均取得了较好的效果。主元分析PCA在降维时考虑数据样本的全局欧式结构,而局部保持投影LPP则可以保持数据样本的局部流形结构,综合PCA与LPP的全局和局部结构保持特性,并考虑部分数据的类别标签信息[12-13],基于最大边缘准则[14]提出一种半监督PCA-LPP流形学习算法,采用UCI数据集对算法的降维性能进行验证,并利用齿轮箱故障实测声发射信号进行了故障特征降维和识别进一步验证,结果表明半监督PCA-LPP方法比PCA和LPP的降维效果好,故障识别准确率更高。
1 半监督PCA-LPP流形学习算法
PCA-LPP流形学习算法结合PCA数据整体分布描述以及LPP数据局部流形信息描述,求解投影矩阵的过程中引入半监督思想,增加有标签样本在学习过程中的权重,同时无标签样本又能有效避免少量有标签样本学习中的过拟合问题。
设在高维空间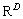 中存在数据集
中存在数据集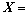
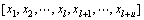 ,
,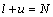 ,其中前l个样本
,其中前l个样本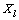 是有标签样本,类别标签个数为c,各类样本数为
是有标签样本,类别标签个数为c,各类样本数为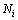 ,
,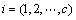 ,后u个样本
,后u个样本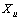 是无标签样本。半监督PCA-LPP所要解决是问题是寻找投影变换矩阵W,将X转换投影为
是无标签样本。半监督PCA-LPP所要解决是问题是寻找投影变换矩阵W,将X转换投影为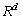 (d<D)空间的数据集Y,即
(d<D)空间的数据集Y,即 。
。
1.1 半监督全局分布描述
全局分布的目标是寻求投影矩阵W,使通过投影后的数据能够在低维空间保持原始样本的大部分方差信息,PCA方法的全局分布目标函数如式1所示。
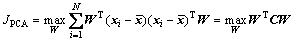 (1)
(1)
其中: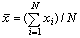 ,
,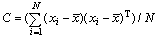 。
。
经典PCA方法不考虑数据分类标签信息,在数据全局分布描述是最优的,但不同类别间的分类能力较差。考虑数据分类标签信息,在PCA目标函数的基础上构造半监督全局目标函数,如下式所示:
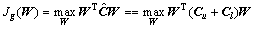 (2)
(2)
其中:矩阵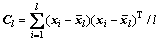 ,
,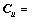
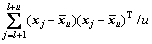 ,
,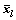 和
和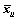 分别为有标签样本和无标签样本的均值。
分别为有标签样本和无标签样本的均值。
1.2 半监督局部流形描述
LPP是无监督流形学习算法,相似权重矩阵不计入样本类别标签信息,易受噪声干扰。引入半监督思想[8],考虑数据的分类标签信息,提出改进半监督相似权重矩阵S的构造方法,如下式所示:
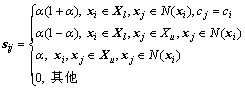 (3)
(3)
其中: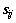 为相似权重矩阵S的元素。
为相似权重矩阵S的元素。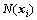 为
为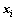 近邻域,
近邻域,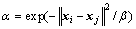 ,热核宽度
,热核宽度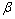 为调节参数,其取值为所有样本对之间欧式距离平均值的平方[15]。
为调节参数,其取值为所有样本对之间欧式距离平均值的平方[15]。
改进后的半监督相似权重矩阵充分考虑了数据样本的标签信息,由于0≤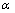 ≤1,故相似权重调节因子1≤
≤1,故相似权重调节因子1≤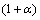 ≤2和0≤
≤2和0≤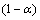 ≤1,样本间欧式距离越近,同类标签样本的相似权值越大,而非同类标签样本的权值相应减小,由于权重调节因子的有界性,噪声干扰被限定在一定的范围内。改进后的半监督相似权值引入样本类别标签信息,既保持近邻域关系又利于样本的分类描述,又具有噪声抑制能力。
≤1,样本间欧式距离越近,同类标签样本的相似权值越大,而非同类标签样本的权值相应减小,由于权重调节因子的有界性,噪声干扰被限定在一定的范围内。改进后的半监督相似权值引入样本类别标签信息,既保持近邻域关系又利于样本的分类描述,又具有噪声抑制能力。
基于半监督相似权重矩阵,给出半监督局部目标函数,如式(4)所示,使LPP的投影矩阵W在保持局部流形的同时能够保持样本间分类信息。
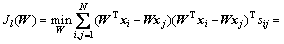
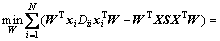
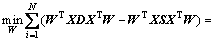
 (4)
(4)
其中:矩阵D为对角线矩阵,对角线元素 ,L=D-S,是拉普拉斯矩阵。为了消除随机尺度因子的影响,求解中限定
,L=D-S,是拉普拉斯矩阵。为了消除随机尺度因子的影响,求解中限定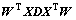 =I,其中I为单位矩阵。
=I,其中I为单位矩阵。
1.3 半监督PCA-LPP整体目标及求解
结合全局目标函数与局部目标函数,基于最大边缘准则[14]构造半监督PCA-LPP整体目标函数,如式(5)所示,目标函数同时考虑PCA与LPP的投影优化约束,使投影后的数据能保留更全面的特征信息。
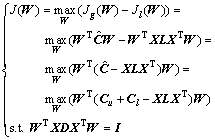 (5)
(5)
整体目标函数可以通过拉格朗日乘子法[16]将式(5)转换为有约束最大值问题,如下式所示:
 (6)
(6)
式(6)对W求导并置0可得
 (7)
(7)
式(7)化简得到式(8),投影矩阵W的求解实质上是求取广义特征向量问题,其中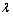 为广义特征值,通过求取d个最大特征值
为广义特征值,通过求取d个最大特征值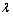 所对应的特征向量,得到投影矩阵W,投影后低维数据通过
所对应的特征向量,得到投影矩阵W,投影后低维数据通过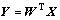 得到。
得到。
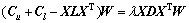 (8)
(8)
总结半监督PCA-LPP流形学习算法的实现步骤如下:
1) 已知样本X,根据式(2)计算构造半监督全局目标函数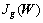 。
。
2) 根据式(3)计算半监督相似权重矩阵S,并根据式4构造半监督局部目标函数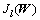 。
。
3) 根据式(5)构造整体目标函数 。
。
4) 求解广义特征方程式(8),得到d个最大特征值对应的特征向量构成投影矩阵W。
5) 根据映射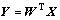 ,得到低维嵌入数据Y。
,得到低维嵌入数据Y。
2 信号特征降维及故障分类识别
信号降维分析中,通过与主流降维方法PCA和LPP比较,验证PCA-LPP的有效性,运算环境为3 GHz i5 CPU,4G RAM,win7以及matlab R2009b。PCA-LPP的降维效率与近邻参数选择有关,近邻参数k通过在一定取值范围内进行逐步寻优计算,保持LPP与半监督PCA-LPP的近邻参数相同。
2.1 UCI样本3降维可视化
采用UCI中的wine数据集[4]对半监督PCA-LPP流形学习算法进行验证,该数据集初始维度为13,共有178个样本,分为3类,第1类样本59个,第2类样本71个,第3类样本48个,设置3类样本有标签数据分别为29,36,24,有标签样本总数为89,在总样本中占一半。分别在数据集上应用PCA,LPP及半监督PCA-LPP进行分析,将样本维度降到3维,其中LPP算法和半监督PCA-LPP算法的近邻参数设置相同,均是k=35,可视化处理结果如图1所示。
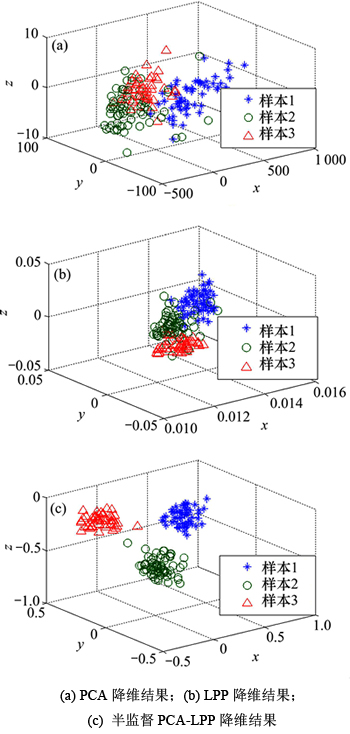
图1 wine数据集三维降维结果
Fig. 1 Dimensionality reduction of wine dataset
从图1可以看出:PCA降维结果中3类样本重叠严重,样本区分度低,LPP降维结果优于PCA,样本类内聚集性提升明显,但不同类别边界附近的重叠严重。PCA-LPP的降维结果效果最好,3类样本的类内聚集性好,且不同类别样本边界距离明显,不同样本类型可以明显识别。其主要原因在于PCA降维仅考虑数据的整体分布方差最大,LPP降维仅保持数据局部流形结构不变,因此LPP比PCA降维结果的类内聚集性好,但二者都没有实现数据整体方差与局部流形结构的兼顾增强,而半监督PCA-LPP同时兼顾了PCA与LPP各自的增强特性,从而使得信号降维效果最好。
2.2 齿轮箱故障信号降维及识别分类
采用齿轮箱故障声发射实测数据对半监督PCA-LPP的降维性能进行分析,实验工况包括正常状态,轴承内圈故障,外圈故障,内外圈复合故障,齿根裂纹故障五种工况,轴承型号为6206,安装在二级传动轴一端,故障齿轮为二级传动轴大齿轮,一级传动比1:2,齿轮箱原理结构及传感器安装如图2所示。声发射采集仪采样频率1 MHz,单个数据样本长度1 s,每种工况对应数据70组,其中30组有类别标签,40组无类别标签,5种工况共350组数据样本。对每个样本用db4小波包进行3层分解,得到每个样本的8个子频带重构分量信号,求取这8个子频带信号的能量熵构建8维特征向量[1]。
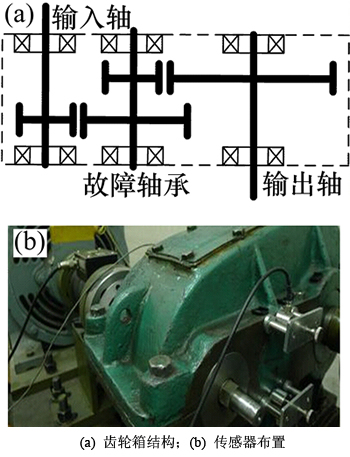
图2 齿轮箱结构及传感器布置
Fig. 2 Gearbox structure and sensor arrangement
采用半监督PCA-LPP,PCA和LPP 3种方法对原始特征进行降维处理,而后将降维后特征输入支持向量机进行训练识别,采用径向基核函数支持向量机,基于交叉验证方法获得核函数参数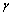 =2.8,惩罚因子c=1.2。对比降维后数据的分类性能,分类识别中选择40组特征作为训练样本,剩余30组作为测试样本。
=2.8,惩罚因子c=1.2。对比降维后数据的分类性能,分类识别中选择40组特征作为训练样本,剩余30组作为测试样本。
2.2.1 半监督PCA-LPP降维识别分析
设置近邻参数k的范围为5~30,间隔为1,降维数d的范围为3~7,间隔为1,交叉验证计算各种参数配比组合下降维后特征的故障识别率。
不同的k和d组合得到的降维结果在支持向量机中的识别率不同,对所有的k和d组合进行计算,结果如图3所示。
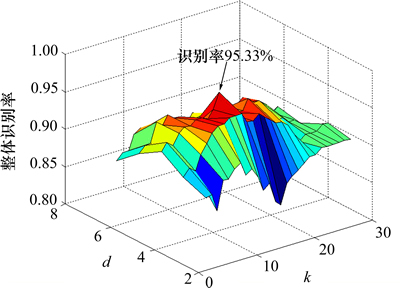
图3 整体识别率随k和d的变化
Fig. 3 Identification rate change by k and d
从图3可以看出:半监督PCA-LPP降维特征的整体识别率随着降维数d和近邻值k的改变不断变化,当降维数d最小时,故障识别率最低,在d和近邻值k变化范围的两端处,故障识别率整体较低,仅当k=15,d=5时,整体识别率达到最高值95.33%。为进一步说明识别率最大值点的参数选择情况,单一固定参数k和d时的识别率曲线如图4所示。从图4可知:
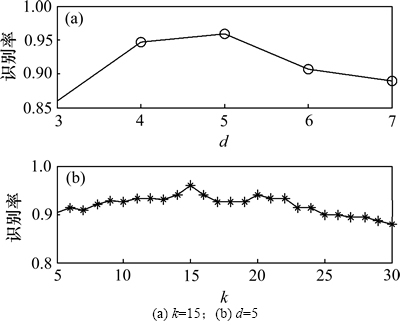
图4 识别率变化曲线
Fig. 4 Curves of identification rate
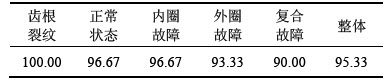
识别率对d的变化比较敏感,识别率对k的变化比较平缓,当k较大时识别率降低明显。k=15,d=5时半监督PCA-LPP降维结果的各类单项识别率如表1所示,其中齿根裂纹识别率最高,复合故障识别率最低,这是因为齿根裂纹与其他几种状态故障具有明显差异,而复合故障特征与内圈故障和外圈故障特征具有相似性。
表1 PCA-LPP降维结果识别率
Table 1 Identification rate of PCA-LPP %
2.2.2 3种降维方法识别性能对比
在k=15和d=5的情况下,对PCA,LPP及半监督PCA-LPP方法的降维特征故障识别情况进行对比。经过3种方法处理后原始特征向量投影到新的低维空间,图5所示为原始高维特征降维后前3个主分量的3维图。从图5可以看出:PCA降维结果最差,不同类别的故障特征混叠严重,LPP的效果比PCA好一些,但是复合故障分布完全混入内圈和外圈故障中。半监督PCA-LPP的分布效果最好,各类别特征聚集性较好,有利于故障类别的辨识。
将k=15和d=5时3种方法降维后的特征输入支持向量机进行故障类别辨识,训练样本与识别样本分配设置与半监督PCA-LPP方法识别分析中设置相同,3种方法的识别结果如表2所示。
从表2可以看到:半监督PCA-LPP方法降维结果对齿轮箱5种故障的识别效果最好,识别率高于PCA和LPP降维结果的识别率。PCA和LPP降维结果单一强调故障特征的整体结构分布方差和局部流形结构,因此故障特征降维后的识别率较低,半监督PCA-LPP方法既考虑部分特征的标签类别信息,又能兼顾整体结构分布方差和局部流形保持,降维后特征能够更好的反映不同故障之间的差异,从而获得更高的故障识别率。
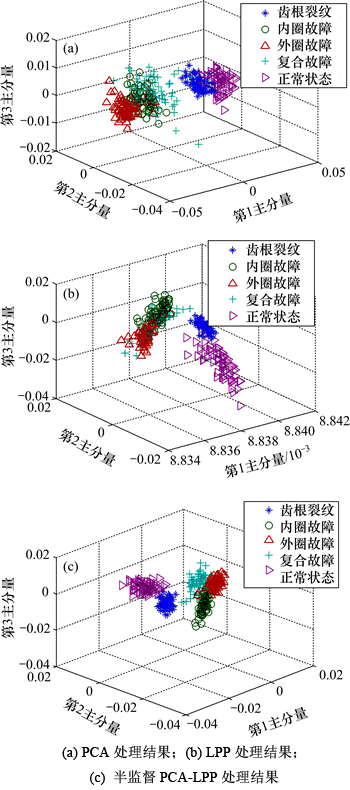
图5 齿轮箱故障信号降维结果
Fig. 5 Dimensionality reduction of gearbox signals
表2 3种降维特征支持向量机识别率对比
Table 2 Support vector machine identification rate of three dimensionality reduction results

3 结论
1) 引入半监督思想,结合PCA与LPP各自的特点,提出半监督PCA-LPP流形学习算法,在数据投影降维过程中同时考虑数据全局分布结构、局部流形结构以及类别标签的判别信息,UCI数据集wine的可视化降维结果表明,半监督PCA-LPP方法的样本分离效果良好。
2) 半监督PCA-LPP方法降维特征向量的支持向量机故障识别率明显高于PCA和LPP方法降维结果,且3种方法降维后特征的前3个主分量3维分布进一步表明了半监督PCA-LPP方法降维结果的在故障分类判别性能上的优势。
参考文献:
[1] 李城梁, 王仲生, 姜洪开, 等. 自适应Hessian LLE在机械故障特征提取中的应用[J]. 振动工程学报, 2013, 26(5): 758-763.
LI Chengliang, WANG Zhongsheng, JIANG Hongkai, et al. Adaptive Hessian LLE in mechanical fault feature extraction[J]. Journal of Vibration Engineering, 2013, 26(5): 758-763.
[2] 孙斌, 薛广鑫. 基于等距特征映射和支持矢量机的转子故障诊断方法[J]. 机械工程学报, 2012, 48(9): 129-134.
SUN Bin, XUE Guangxin. Method of rotor fault diagnosis based on isometric feature mapping and support vector machine[J]. Journal of Mechanical Engineering, 2012, 48(9): 129-134.
[3] 尹刚, 张英堂, 李志宁, 等. 基于MSPCA的缸盖振动信号特征增强方法研究[J]. 振动与冲击, 2013, 32(6): 143-147.
YIN Gang, ZHANG Yingtang, LI Zhining, etal. Fault feature enhancement method for cylinder head vibration signal based on multiscale principal component analysis[J]. Journal of Vibration and Shock, 2013, 32(6): 143-147.
[4] 刘忠宝, 潘广贞, 赵文娟. 流形判别分析[J]. 电子与信息学报, 2013, 35(9): 2047-2050.
LIU Zhongbao, PAN Guangzhen, ZHAO Wenjuan. Manifold- based discriminant analysis[J]. Journal of Electronics & Information Technology, 2013, 35(9): 2047-2050.
[5] 赵振华, 郝晓弘. 局部保持鉴别投影及其在人脸识别中的应用[J]. 电子与信息学报, 2013, 35(2): 463-466.
ZHAO Zhenhua, HAO Xiaohong. Linear locality preserving and discriminating projection for face recognition[J]. Journal of Electronics & Information Technology, 2013, 35(2): 463-466.
[6] 李锋, 汤宝平, 宋涛, 等. 归一Laplacian矩阵有监督最优局部保持映射故障辨识[J]. 机械工程学报, 2013, 49(13): 100-106.
LI Feng, TANG Baoping, SONG Tao, et al. Fault identification method based on normalized laplacian-based supervised optimal locality preserving projection[J]. Journal of Mechanical Engineering, 2013, 49(13): 100-106.
[7] HE X F, NIYOGI P. Locality preserving projections[C]// Neural Information Processing Systems16. Vancouver: MIT Press, 2004: 153-160.
[8] FADI D, AMMAR A. Enhanced and parameterless locality preserving projections for face recognition[J]. Neurocomputing, 2013, 99(1): 448-457.
[9] MAO Yu, ZHOU Yanquan, YU Hao, et al. Semi-supervised locality discriminant projection[J]. Procedia Engineering, 2012, 29(3): 1319-1324.
[10] WONG W K, ZHAO H T. Supervised optimal locality preserving projection[J]. Pattern Recognition, 2012, 45(1): 186-197.
[11] DENG Xiaogang, TIAN Xuemin. Sparse kernel locality preserving projection and its application in nonlinear process fault detection[J]. Chinese Journal of Chemical Engineering, 2013, 21(2): 163-170.
[12] 黄鸿, 秦高峰, 冯海亮. 半监督流形学习及其在遥感影像分类中的应用[J]. 光学精密工程, 2011, 19(12): 3025-3028.
HUANG Hong, QIN Gaofeng, FENG Hailiang. Semi-supervised manifold learning and its application to remote sensing image classification[J]. Optics and Precision Engineering, 2011, 19(12): 3028-3028.
[13] 王健, 冯健, 韩志艳. 基于流形学习的局部保持PCA算法在故障检测中的应用[J]. 控制与决策, 2013, 28(5): 683-687.
WANG Jian, FENG Jian, HAN Zhiyan. Locally preserving PCA method based on manifold learning and its application in fault detection[J]. Control and Decision, 2013, 28(5): 683-687.
[14] 袁暋, 程雷, 朱然刚, 等. 一种新的基于MMC和LSE的监督流形学习算法[J]. 自动化学报, 2013, 39(12): 2076-2079.
YUAN Min, CHENG Lei, ZHU Rangang, et al. A new supervised manifold learning algorithm based on MMC and LSE[J]. Acta Automatica Sinica, 2013, 39(12): 2076-2079.
[15] 李锋, 王家序, 杨荣松. 有监督不相关正交局部保持映射故障辨识[J]. 仪器仪表学报, 2013, 34(5): 1113-1116.
LI Feng, WANG Jiaxu, YANG Rongsong. Fault identification method on supervised uncorrelated orthogonal locality preserving projection[J]. Chinese Journal of Scientific Instrument, 2013, 34(5): 1113-1116.
[16] 宋涛, 汤宝平, 李锋. 基于流形学习和K-最近邻分类器的旋转机械故障诊断方法[J]. 振动与冲击, 2013, 32(5): 149-153.
SONG Tao, TANG Baoping, LI Feng. Fault diagnosis method for rotating machinery based on manifold learning and K-nearest neighbor classifier[J]. Journal of Vibration and Shock, 2013, 32(5): 149-153.
(编辑 陈爱华)
收稿日期:2015-07-22;修回日期:2015-10-19
基金项目(Foundation item):国家自然科学基金资助项目(50775219);军队科研资助项目([2011]107) (Project(50775219) supported by the National Natural Science Foundation of China; Project([2011]107) supported by the Military Research Foundation)
通信作者:唐力伟,博士,教授,从事机械性能检测与故障诊断研究;E-mail: tom5157@163.com