Motif Finding问题的分布式参数算法
张祖平,王 丽
(中南大学 信息科学与工程学院,湖南 长沙,410083)
摘 要:基于从DNA序列形成k分图的图理论算法和查找k-clique的理论算法,设计与实现了对Motif Finding问题求解的分布式参数算法。该算法的主要特点是:采用新的1-3树分枝算法并实现分布式计算机制,即任务可以随着计算过程的展开在每一阶段不断地分解并分布到不确定数量的申请参与计算的客户机上,服务器端负责任务均衡与结果整合。实验结果表明:分布式参数算法充分利用多台机器协同计算,能够正确、高效地得到计算结果,为求解生物计算中难解的Motif Finding问题提供了有效的解决手段。
关键词:Motif;k分图;团;生物计算;分布式系统
中图分类号:TP311 文献标识码:A 文章编号:1672-7207(2007)05-0943-07
Distributed parameterized algorithm for Motif Finding
ZHANG Zu-ping, WANG Li
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Based on the graph-theoretic algorithm, which is used to generate k-partite graph from DNA sequences, and a theoretic algorithm which is used to search k-clique in k-partite graph, a new distributed parameterized algorithm is designed and implemented to solve Motif Finding problem. The main characteristics of this algorithm are the introduction of 1-3 tree branching algorithm and the implementation of distributed mechanism, i.e., task can be constantly decomposed into several tasks as program proceeding at each phase, and then these tasks are distributed to several client computers which is applied for participation of calculation. On the server, the tasks are distributed and balanced as well as the results are received and combined. Experimental results show that this distributed parameterized algorithm is correct and efficient since it makes full use of computing capability of many computers, and provides an effective approach to solving the difficult problems in biocomputing such as Motif Finding.
Key words: Motif; k-partite graph; clique; biocomputing; distributed system
生物信息学是新兴的交叉学科,它综合运用数学、计算机科学和生物学的各种工具,来阐明和理解大量数据所包含的生物学意义[1]。其中,对基因突变热点区的检测[2]是当前研究的热点,而在扩展的多重序列比对方面还处于试验探索阶段。已经证明Motif Finding是NP难问题[3],它是生物计算中较早被深入研究的问题之一,也是近年来研究的热点问题[4-6],虽然已经出现一些优秀的软件工具,如:基于贪婪算法的CONSENSUS[7],基于Gibbs取样的GibbsDNA[8]和基于EM算法的MEME[9]等,但是,这些算法并不能确保一定能找到确实存在的Motif,因为它们都需要一个很好的开始点,所以,都是不确定算法;另外,基于详尽的列举所有可能的Motifs算法,虽然能保证找到最优的Motif,但是,运行时间随着Motif长度l的增加而呈指数增长,在l较大的挑战问题中变得不可行。为解决上述问题,本文作者一方面引进参数算法求解Motif Finding问题的所有精确解,有效解决非确定算法遗漏结果的问题;另一方面,引进分布式计算方法与分布式求解系统[10],将计算任务划分成较小的可以独立执行的单元,并分布到网络上有空闲计算资源的多台机器中去,系统将各机器返回的计算结果进行合并处理后形成问题的最终结果,从而加快了Motif Finding问题的求解过程。
1 关键算法设计与分析
1.1 问题分析
依照Pevzner 的(l, d)-motif模型[11]随机产生k个长度均为n的随机序列,在每个序列中随机挑选1个位置置入1个(l, d)-motif,该Motif基于1个长为l允许有d个突变的模式P产生。Motif Finding问题要求在不知道模式P和置入位置的情况下找出这些置入的Motif。
根据文献[12],算法分为2步:第1步,应用Pevzner的图理论算法[11]从DNA序列产生k分图:在每个序列Si中的第j个位置,建立1个顶点Sij,表示1个从位置j(1≤j≤n-l+1)开始的长为l的子串,若i≠p并且Sij和Spq之间的距离不超过2d(突变元素的数量),则用1条边将2个顶点Sij和Spq相连;第2步,参考查找k-clique的理论算法[12],应用分治方法从k分图中求解k-clique:将得到的k分图细分为k′(k′<k)分图直到k′小到容易解决为止,求得k′-clique之后再合并为所求的k-clique。求得的k-clique即为所求的Motif及其置入位置。
1.2 k分图形成算法
1.2.1 算法思想
根据图理论,算法形成k分图的关键在于判断2个顶点间是否存在边,即计算2个字符串之间的不匹配个数是否在允许范围之内,而图理论算法并未给出有效的方法。通过研究,已有算法如PROJECTION[13],WINNOWER,SP-score[11]及最新的判据搜索算法[14]等都只考虑了简单的替换突变,不能处理存在插入和删除突变的序列。为解决这个问题,本文从Mismatch Tree[15]算法中得到启发,设计了1-3树分枝算法。因为这种算法在逻辑上是一个树的形式。其中,“1”代表匹配时只产生1个分枝,“3”代表不匹配时产生3个分枝。
当2个字符串A与B进行比较时,若在某一位置出现了不匹配,则该位置上的字符可能产生了替换、插入或删除突变。首先,对3种突变进行算法抽象。
a. 替换。无论A与B中任何1个产生了替换突变,甚至都产生了突变,其结论都是跳过A与B在该位置上的字符,并将不匹配个数计数器增加1。
b. 插入和删除。将2个字符串进行比较,插入和删除突变都是相对于另一条字符串而言的。若在某个位置上A相对B发生了插入突变,则相当于B相对A发生了删除突变,这时,应该忽略该位置上A的字符,用A下一个位置上的字符继续与B的该位置上字符比较,同时不匹配个数计数器加1。
1-3树分枝算法为:
boolean done=false; /* 结束标志 */
int mis=0; /* 不匹配个数 */
int pos1=0; /*字符串A将要进行比较的字符位置*/
int pos2=0; /*字符串B将要进行比较字符的位置*/
while (true) {
if (done) then return;
if (pos1到了字符串A的尽头 or pos2到了字符串B的尽头 or mis>所允许的最大不匹配个数) then break;
if (pos1位置上的字符与pos2上的字符一样) then {
pos1++;
pos2++;
continue;
}
else {
mis++;
产生假设是插入突变的线程,传值pos1+1, pos2, mis;
产生假设是删除突变的线程,传值pos1, pos2+1, mis;
假设是替换突变,pos1++, pos2++;
continue;
}
}
if (mis <= 允许的最大不匹配个数) then{
if (done) then return;
synchronize {
if (done) then return;
done = true;
将这条边加入k分图;
}
}else return;
为了更好地理解这个算法,下面给出比较字符串actta…… 和attag……时程序产生的线程树,其中a, c, t, g为4个碱基,如图1所示。

图1 应用1-3树分枝算法比较2个字符串示例
Fig.1 Comparison between two sequences with 1-3 tree branching algorithm
线程树是一个逻辑上的概念,实际上并不存在,可以看成是线程运行的轨迹。1个分枝代表1个线程,每个线程都拥有自己的一些资料,如不匹配个数计数器,与2个字符串各自比较到了哪个字符等。
1.2.2 算法分析
比较2个长为l的字符串,允许不匹配个数为2d,该算法的时间复杂度在最好情况下为l,最坏情况下为 ,d一般不大。在一条长为n的序列中,把其中长为l的字符串当做k分图中的1个顶点,则共有
,d一般不大。在一条长为n的序列中,把其中长为l的字符串当做k分图中的1个顶点,则共有 个顶点。
个顶点。
第1条序列中的顶点与其后的k-1个序列中的所有顶点进行比较,即进行(k-1)(n-l+1)2次顶点比较;
第2条序列中的顶点与其后的k-2个序列中的所有顶点进行比较,即进行(k-2)(n-l+1)2次顶点比较;
……
将倒数第2条序列即第k-1条序列中的顶点与最后那条序列中的所有顶点进行比较,即进行(n-l+1)2次顶点比较;
最后,那条序列即第k条序列不再与任何序列进行比较。
所以,比较次数共为:
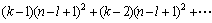
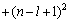 =
=
 =
= 。
。
因而,形成k分图在最好情况下的时间复杂度为:O(lk2(n-l)2);最坏情况下的时间复杂度为: O(32d k2(n-l)2)。
由于该算法运行时产生的线程不确定,最好和最坏情况的发生概率均趋于0,经实验验证,在k, n和d不大(k = 10, n = 82, d = 4)但要求精确解的情况下,实际计算可行。
1.3 k-clique寻找算法
1.3.1 算法思想
查找k-clique的理论算法采用了从上至下的递归方法来实现分治策略,实际上更为有效的方式是采用自下而上的循环方法来实现分治,这样可以获得更高的效率,便于将算法进行分布式处理,并且只需将算法稍作修改便可求解更加复杂的最大团问题[12]。具体方法如下。
将k分图划分为一些k′分图(k′<k),从k′分图中求解k′-clique后再将k′-clique组合成k″-clique(k′<k″<k),直至最后组合成k-clique。若最后无法将k″-clique组合成k-clique,则可以判定k分图至少存在大小为k’’的clique,修改程序,利用这些中间结果可以方便地求出k分图的最大团。k′的选择应该使得子图足够稀疏以至于很容易解决。由于受存储结构的制约(存储的是边),k′选择4最恰当。
当序列个数不是4的倍数时,若只剩1条序列,则把它的所有顶点看成1-clique;若余下2条序列,则把这2条序列间的边看作2-clique;若余下3条序列,则把2条序列间的2-clique和1条序列的1-clique结合得到3-clique。
1.3.2 算法分析
当k为2的整数(>1)次幂时,时间复杂度最大。这里分析这种时间复杂度最大的情况。考虑最坏的情况,即k分图是完全图,这意味着每2个顶点间都有边,每条序列有 个顶点,则每2条序列间有(n-l+1)2条边,每4条序列中有(n-l+1)4个4-clique。
个顶点,则每2条序列间有(n-l+1)2条边,每4条序列中有(n-l+1)4个4-clique。
算法首先用2条序列间的所有边(即2-clique)与另2条序列间的所有边进行比较,得到一组4-clique;然后,用一组4-clique与另一组4-clique进行比较,得到一组8-clique,……。直到最后比较2组k/2-clique,检查是否存在k-clique。
第1步:求出所有4-clique,时间复杂度为:
 。
。
第2步:求出所有8-clique,时间复杂度为:
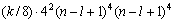 。
。
…
最后1步即第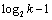 步:求出所有k-clique,时间复杂度为:
步:求出所有k-clique,时间复杂度为:
 。
。
推出通用公式为(m代表第m步),时间复杂度为:
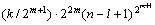 =
=
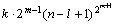 。
。
总的时间复杂度为:



 。
。
实际计算的时间复杂度远小于此时间复杂度,并且由于是应用分布式系统并行求解,故运行时间在可承受范围之内。
2 关键数据结构设计
2.1 k分图
k分图共有 个顶点,为方便读取顶点信息,在存储文件的头部存储1个顶点索引。
个顶点,为方便读取顶点信息,在存储文件的头部存储1个顶点索引。
k分图的数据结构采用邻接表,即在1个顶点中存储另1个顶点的位置来表示1条边,在序号较小的顶点中存储所有与之相连的序号较大的顶点位置,即在顶点Sij里存储数组(p, q),其中i<p。若顶点Sij与Spq间有边,则进一步将顶点按其属于哪个序列进行分类,只存储在此序列中的位置,即只存储q,节省了一半空间。
顶点采用Vector数据结构。下面给出顶点(0, 3)的存储结构示例图。假设该顶点与(1, 2),(1, 5),(1, 6),(2, 4),(3, 8),(3, 9)等顶点相连,则该顶点的数据结构如图2所示。

图2 顶点Vector的数据结构
Fig.2 Data structure of vertex
2.2 团
由于团的大小与序列个数是一样的,因此,用1个确定长度的数组来存储;团中的元素是顶点,用长度为2的数组表示。综上所述,团的数据结构是1个二维数组,第1维长度为计算的序列个数,第2维长度为2。结果中团的个数不确定,因此,用Vector来存储这些团。
3 算法分布式思想及其实现
参数算法虽然能够用于有效求解精确解,但是,时间复杂度仍然随问题规模呈指数增长,因此,为加快求解速度,引入分布式机制,将算法进行分布式处理,使之能在分布式平台上运行,并设计动态均衡模型,保证负载均衡。
分布式系统采用一个服务器控制多台客户机的模式,其中服务器只负责产生任务与接收客户机传回结果及整合,客户机对分给自己的任务进行计算。客户机端的程序思想如前所述,但计算任务由从服务器得到的任务参数决定,规模比总的任务小得多。我们下面介绍的分布式处理算法都是指服务器端程序采用的算法。
3.1 生成k分图
为了使分解出的任务规模相近,采用对序列进行垂直平分的方法,如图3所示,其中水平的粗线条代表1条DNA序列,前端的实线部分代表要比较的顶点,长为(n-l+1)。为了平均分割任务,这里将实线部分用垂直的虚线进行平分,划分出的每1截对应于比较时的一个顶点。

图3 垂直平分DNA序列里的顶点比较任务
Fig.3 Vertically average division of comparing task
当n-l+1不能被所分份数整除时,将余数平均分给前几个任务,保证大的任务数仅比小的任务数大1,并且先产生先被取走执行,减少了对系统效率的影响。
将分解后的任务分配给客户机进行计算。以图3所示序列为例。假如1台客户机分到了第2个任务,那么,它将用第1个序列由虚线分成的第2个部分的顶点与第2,3和4个序列的全部顶点进行比较,然后,用第2个序列的第2部分顶点与第3和4个序列的全部顶点进行比较,最后,用第3个序列的第2部分顶点与第4个序列的全部顶点进行比较。比较完后把结果传回服务器,服务器将其与其他客户机传回结果进行整合,得到k分图。
整合操作是当服务器得到一个返回结果时,把结果文件中除了索引以外的部分全部拷贝(为防止内存溢出,采用依次拷贝结果文件定长的一部分策略)到一个指定的新文件里,并用结果文件的索引对新文件的索引进行修正。这个新文件在第1个结果返回时创建,并且在开始部分放入一个空的long[k-1][n-l+1]数组用来索引全部顶点。
3.2 查找k-clique
在这一步里,如何分解任务并使得任务的粒度合适是很关键的。因为经验表明,如果粒度过小,将使系统频繁建立连接传输文件,严重影响系统效率;若粒度过大,则无法充分利用分布式系统的资源。另外,对k’-clique的结合方法将影响系统负载均衡和计算资源的利用。这里介绍一个动态的均衡模型以解决这个问题。
为了充分利用分布式系统资源,在应用分治法将序列分成4个1组的同时,还将每个组的任务细分。具体做法如下。
以每组的第1个序列作为基准序列,从第1个顶点开始,把所有与这个顶点有关的计算任务放在一起,一直到最后1个顶点,最终形成n-l+1个任务。有关的任务是指该组中与这个顶点的判定有关的顶点和边。具体来说,第1个任务是第1个序列的第1个顶点和第2个序列顶点间的所有边与第3和第4个序列间所有边的组合判定,直到第n-l+1个任务为止。经测试,这样的粒度是合适的,若有1种合适的检测控制粒度的算法将更加有效地提高系统效率。
由于得到k′-clique后需要再将k′-clique组合成k″-clique(k′<k″<k=,则需要将结合2个k′-clique得到k″-clique作为新的判定任务并分配给客户机进一步计算。如果只是简单地返回了2个组就将其结合进入下一层循环,那么,必定使得下一层的后一组比前一组晚很多才能产生,这样,势必影响更下一层的结合,最终使系统效率下降。为了克服这个时间缺陷,设计了一个动态结合组的模型,为了便于理解,在介绍这个模型之前先介绍克服上述缺陷的静态模型。如图4所示,假设产生了奇数个分组并且各个组的任务其结果是按发出去的顺序依次返回的,其中有斜线填充的2个矩形代表同一个组,这个组是第1层中最后1个完成的(这里称从上到下的一排排矩形为第1层、第2层,……),而又比第2层的所有任务先返回,那么,该组将移到第2层的最前面与其他组结合。这个模型能够克服时间缺陷的原因是,每层先完成的组在选择与其进行结合的组时,选择的是没有结合过的组中完成顺序居中的那个。

图4 克服了时间缺陷的静态模型
Fig.4 Static combining model without time flaw
每个组分成n-l+1个小任务,可能返回0~ n-l+1个结果,若为0,则程序结束运行,要寻找的k-clique不存在;若为n-l+1,直接将这些结果与另外一组结果进行结合,则最多可能有(n-l+1)2个任务;若继续结合下去,则任务数将呈指数增长,必须将一个组里的结果先进行合并,然后,再与另一组里的任务结合,这样,结合后的组里最多只有n-l+1个任务。另外,不必等2个组的任务全部返回才开始结合,在其中一个组的任务全部返回合并后就可以与另一个只有部分返回结果的组进行结合。
在实现动态模型时,采用文件夹来存储任务的返回结果,文件夹可以动态创建与释放。下面用一个假设的例子来说明这个动态模型的工作过程。如图5所示,当1个组里的结果全部返回并且合并为1个时就用横线填充矩形来表示。完成顺序是否居中,用剩余任务(即已经产生但还没有结果返回的任务)的多少来衡量。假设一共分了7组,前6组都是4个序列1组,分解成小任务之后分发出去,最后,1组只有2个序列,直接从最后2个序列里得到的所有边作为2-clique放入第6个文件夹,这时第6个文件夹已满,它去寻找能够与它进行结合的文件夹。但是,没有一个文件夹里有返回的结果,所以,它填写注册信息,以期将来有某个文件夹发现它并与它结合。当第0号文件夹的第1个结果返回时系统扫描注册信息,发现第6号文件夹并与之结合,动态创建文件夹7来存放将来的返回结果。假设当第1号文件夹满时第2,3和4号文件夹分别还有3,2和5个任务没有返回,若第5号文件夹还是空的,则第1号文件夹就选择文件夹2进行结合,创建文件夹8;当文件夹3满时,文件夹5的剩余任务数小于文件夹4的剩余任务数,则选择与文件夹5结合,生成文件夹9;当文件夹4满时,由于它是本层的最后一个,无法与本层的文件夹结合,因此,将它的层数加1,把它放入下一层与下一层的文件夹结合。根据图5,它与文件夹8结合,生成文件夹10。当文件夹7与文件夹9结合时,由于文件夹7已经完成所有任务,文件夹0和6都已被释放,所以,重复利用文件夹0来存放将来的结果。最后,文件夹10与0结合,重复利用文件夹1,将最终结果存放在文件夹1中。

图5 动态结合组模型
Fig.5 Dynamic combining model
4 实验结果验证与讨论
4.1 判断2个顶点间是否有边
3个序列组匹配的测试结果如表1所示。其中,距离指编辑距离。匹配序列组中大写字符代表匹配的字符,小写字符代表不匹配的字符,插入和删除突变的则对应“-”。
表1 序列组匹配的验证实例
Table 1 Test results of comparing sequences

从验证1看出,1-3树分枝算法对于只存在替换突变的序列比对可以胜任;验证2表明,当存在插入和删除突变时,1-3树分枝算法同样有效;验证3表明,在处理1条序列产生了几个连续的插入突变这样的极端情况时,1-3树分枝算法仍然有效,而Mismatch Tree[15]算法不能有效处理这种情况。
4.2 寻找k-clique
测试基于在k=10, n=82的模拟范例序列中寻找(15, 4)-motif,性能结果如图6所示。

图6 多台客户机运行时间测试结果
Fig.6 Test results of multiple clients
从测试性能结果可以看出,分布式计算机制大大缩短了程序运行时间。虽然本文的算法要求第1步求k分图的任务全部完成返回后才能开始第2步的计算,但是,在该测试中,由于在第1步分解任务时有几台客户机参与计算就平均分解成几个任务,大的任务比小的任务最多大1,大的任务先被取走计算,所以,空等待时间很少。
对这个范例序列进行实际计算后,得到3 000多个团,而实际上范例里标出的团只有2个。经过分析验证,确定本文的算法与程序是正确的,产生这样的结果是因为Motif Finding问题本身就是一个结果数量众多的问题,用精确算法得到结果后,还要用生物学知识进一步选择处理才能找出真正正确、有效的结果。
5 结 论
a. 研究了Motif Finding问题的精确算法,提出了1-3树分枝算法,有效地解决了问题向图转换时存在突变时难以表达的关键问题。
b. 设计了Motif Finding问题的分布式参数算法,采用对序列垂直划分的方法将计算任务分布化,同时设计了静态与组合模型解决任务负载均衡的问题。
c. 实现了精确求解Motif Finding问题的分布式计算系统。实验结果表明,设计与实现的分布式算法与计算系统能有效求解问题实例,并在多机共同计算时具有较好的协同性。
参考文献:
[1] Krawetz S A, David D. Introduction to bioinformatics: A theoretical and practical approach[R]. Totowa: Humana Press, 2003.
[2] 孙 霞, 殷鑫浈, 邬玲仟, 等. 弥漫性掌跖角化病家系角蛋白9基因突变热点区的检测[J]. 中南大学学报: 医学版, 2005, 30(5): 521-524.
SUN Xia, YIN Xin-zhen, WU Ling-qian, et al. Hotspot of the mutations of keratin 9 gene in a diffuse palmoplantar keratoderma family[J]. Journal of Central South University: Medicine Science, 2005, 30(5): 521-524.
[3] YU Jiang-sheng. NP completeness [R]. Beijing: Peking University, Institute of Computational Linguistics, 2003.
[4] Chin F, Leung H, Yiu S M, et al. Finding motifs for insufficient number of sequences with strong binding to transcription factor[C]//RECOMB04. San Diego: ACM Press, 2004: 125-132.
[5] Rajasekaran S, Balla S, Huang C H. Exact algorithms for planted motif problems[J]. Journal of Computational Biology, 2005, 12(8): 1117-1128.
[6] Shapiro J, Brutlag D. FoldMiner: Structural motif discovery using an improved superposition algorithm[J]. Protein Science, 2004, 13: 278-294.
[7] Hertz G Z, Stormo G D. Identifying DNA and protein patterns with statistically significant alignments of multiple sequences[J]. Bioinformatics, 1999, 15(7): 563-577.
[8] Lawrene C E, Altschul S F, Boguski M S, et al. Detecting subtle sequence signals: A Gibbs sampling strategy for multiple alignment[J]. Science, 1993, 262(5131): 208-214.
[9] Bailey T L, Elkan C. Fitting a mixture model by expectation maximization to discover motifs in biopolymers[C]//Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. California: AAAI Press, 1994: 28-36.
[10] 王建新, 莫秋菊. 基于Internet的通信系统虚拟实验环境设计与实现[J]. 中南大学学报: 自然科学版, 2006, 37(2): 128-133.
WANG Jian-xin, MO Qiu-ju. Design and implementation of communication system virtual environment based on Internet[J]. Journal of Central South University: Science and Technology, 2006, 37(2): 128-133.
[11] Pevzner P A, Sze S H. Combinatorial approaches to finding subtle signals in DNA sequences[C]//Proceedings of the 8th International Conference on Intelligent Systems for Molecular Biology. La Jolla: AAAI Press, 2000: 269-278.
[12] Sze S H, CHEN Jian-er. Find specific motifs in DNA sequences via cliques in k-partite graphs[R]. Texas A&M University: Departments of Computer Science and Biochemistry & Biophysics, 2003.
[13] Buhler J, Tompa M. Finding motifs using random projections[C]//Proceedings of the 5th Annual International Conference on Computational Molecular Biology. Montreal: ACM Press, 2001: 69-76.
[14] 李冬冬, 王正志, 杜耀华, 等. DNA序列中模式发现的一种快速算法[J]. 生物物理学报, 2005, 21(2): 121-129.
LI Dong-dong, WANG Zheng-zhi, DU Yao-hua, et al. A fast Motif Finding algorithm for dna sequence[J]. Acta Biophysica Sinica, 2005, 21(2): 121-129.
[15] Eskin E. Sparse sequence modeling with applications to computational biology and intrusion detection[D]. New York: Columbia University, 2002.
收稿日期:2006-12-15;修回日期:2007-01-08
基金项目:国家自然科学基金资助项目(60433020)
作者简介:张祖平(1966-),男,湖南湘乡人,博士,教授,从事参数计算与应用及大型数据库技术研究
通信作者:张祖平,男,教授;电话:0731-8877936;E-mail: zpzhang@mail.csu.edu.cn