J. Cent. South Univ. Technol. (2008) 15: 877-881

DOI: 10.1007/s11771-008-0160-2

Retrieval of canopy biophysical variables from remote sensing data using contextual information

XIAO Zhi-qiang(肖志强)^{1, 2}, WANG Jin-di(王锦地)^{1, 2}, LIANG Shun-lin(梁顺林)³,

QU Yong-hua(屈永华)^{1, 2}, WAN Hua-wei(万华伟)^{1, 2}

 (1. State Key Laboratory of Remote Sensing Science

Jointly Sponsored by Beijing Normal University and Institute of Remote Sensing Applications,

Chinese Academy of Sciences, Beijing 100875, China;

2. School of Geography, Beijing Normal University, Beijing 100875, China;

3. Department of Geography, University of Maryland, College Park, MD 20742, USA)

Abstract: In order to improve the accuracy of biophysical parameters retrieved from remotely sensing data, a new algorithm was presented by using spatial contextual to estimate canopy variables from high-resolution remote sensing images. The developed algorithm was used for inversion of leaf area index (LAI) from Enhanced Thematic Mapper Plus (ETM+) data by combining with optimization method to minimize cost functions. The results show that the distribution of LAI is spatially consistent with the false composition imagery from ETM+ and the accuracy of LAI is significantly improved over the results retrieved by the conventional pixelwise retrieval methods, demonstrating that this method can be reliably used to integrate spatial contextual information for inverting LAI from high-resolution remote sensing images.

Key words: inverse problem; canopy biophysical variables; contextual information; leaf area index

1 Introduction

Canopy biophysical variables, such as leaf area index (LAI), are important input or output parameters of some dynamic process models such as crop growth models, land surface models, and have been widely applied to large area water and carbon cycle simulation, climatic modeling and global change research. Therefore, it is important to precisely estimate canopy biophysical variables at the regional or global scale. And remote sensing, which has been widely used in various fields^[1-2], provides a unique way to obtain canopy biophysical variables.

Currently, there are many methods to estimate biophysical variables from remote sensing data. And they can be roughly divided into following classes: by statistical relationship between LAI and spectral vegetation indices, by physical model inversion and by other nonparametric methods^[3-4]. These methods have their own usefulness and limitations. Since the model inversion methods are physically based and can adjust to a wide range of situation^[5], radiative transfer models are more frequently used in the inverse mode to estimate the canopy biophysical variables from remote sensing data^[6-7].

However, the usual approaches to retrieve biophysical variables from remote sensing data are limited to pixelwise retrieval, and there are only a few on the parameter retrieval from remote sensing data using spatial contextual information^[8].

There are generally two main types of contextual information^[9], that is, interpixel surface characteristic dependency context and interpixel correlation context. And in many remotely sensed images, especially the high-resolution remote sensing images, objects on the ground are much greater than the pixel element size so that neighboring pixels are more likely to come from the same class and form a homogeneous region. And the neighboring pixels from the same class always possess identical or similar surface characteristic parameters.

Therefore, it makes sense to introduce the related information among the neighboring pixels in the parameter retrieval process to estimate canopy biophysical variables accurately from remote sensing data. In this work, a new method was put forward to retrieve canopy biophysical variables using the contextual information of remote sensing data. Starting from the posterior probability formula defined by TARANTOLA^[10], a cost function was constructed to retrieve canopy biophysical variables from remote sensing data using contextual information. Retrieval of LAI from ETM+ data using this method was finally illustrated.

2 Retrieval method

2.1 Conventional method for parameter retrieval

Given a set of remote sensing measurements, the conventional inversions of physically-based canopy reflectance model determine the set of canopy biophysical variables m by minimizing the cost function defined in Eqn.(1) such that the simulated reflectances optimally fit the measured reflectances^[11-12].

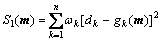                   (1)

where  k=1, 2, …, n; d_k and g_k(m), are the remote sensing measurements and reflectances simulated from the model respectively, and ω_k is the weighting coefficient.

In general, these inversion problems are ill-posed mainly because of the non-unique solution and the measurement and model uncertainties^[13-14]. To reduce the uncertainties associated to the estimation of canopy biophysical variables in the radiative transfer model inversion process, the prior information of biophysical variables is used to solve the ill-posed problems^{[13, 15-16]}.

Let M be the model space, and D the data space. TARANTOLA^[10] defined the posterior probability density in space D×M as follows:

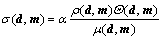                   (2)

where  α is a normalization constant, m and d are vectors in model space and data space respectively, ρ(d, m) is the prior probability density in space D×M, which represents both information obtained on the observable data d and prior information on the model parameters m, Θ(d, m) is the theoretical probability density which constructs the physical correlations between d and m, and μ(d, m) represents the homogeneous state of information. Then, the posterior information in the model space is given by the marginal probability density

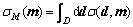                       (3)

Using Eqn.(2) and Eqn.(3), the posterior information in the model space is

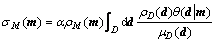           (4)

where  θ(d|m) is a probability of d for every given model m.

Assume that the model parameters, the observation variables and the prior information m_p on the model parameters are Gaussian, then there exists

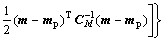          (5)

where  C_D is the covariance matrix representing the measurement uncertainties and model uncertainties, and C_M is the covariance matrix representing the uncer- tainties of a prior information on the model parameters.

Thus, the retrieval of canopy biophysical variables from remote sensing data consists in searching for the maximum likelihood of the posterior probability density function σ_M(m) of canopy biophysical variables, or minimizing the cost function defined in Eqn.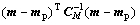(6).

                (6)

Eqn.(6) incorporate the observational data and the prior information of canopy variables. And the cost function has been widely used in the parameter retrieval from remote sensing data. However, the cost function, constructed just using the individual pixel measurement and prior information on the model parameters, makes no use of the related vegetation parameter information among the neighboring pixels.

2.2 Parameter retrieval using contextual information

In order to improve the accuracy of the parameter retrieval from remote sensing data, an attempt was made to retrieve canopy biophysical variables using the contextual information.

As shown in Fig.1, the observational information at pixel (i, j) and its 4-neighboring pixels are used to estimate canopy biophysical variables at pixel (i, j). Then, the data space is extended as D=D_{i, j}×D_{i-1, j}×D_{i, j-1}×  D_{i, j+1}×D_{i+1, j}, in which each vector is d(d=(d_{i, j}, d_{i-1, j},

Fig.1 Nearest neighbours of pixel (i, j)

d_{i, j-1}, d_{i, j+1}, d_{i+1, j})). Therefore, the posterior probability density in the model space can be expressed as follows:

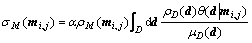     (7)

Assume conditional independence of m_i±1,j, m_i,j±1 of the 4-neighbours of pixel (i, j) for a given m_{i, j}, then, Eqn.(7) can be extended as

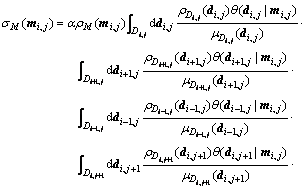
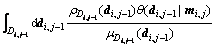(8)

where  the first integral term, similar to the integral term in Eqn.(4), represents the parameter retrieval constraint from the observational data at pixel (i, j), and the latter four integral terms represent parameter retrieval constraints from the observational data at the 4-neighbor pixels.

Assume that the model parameters, the observation variables and the prior information on the model parameters are Gaussian distribution, then, the first integral term in Eqn.(8) can be written analogously as follows:

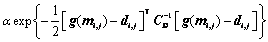(9)

And the second integral term is

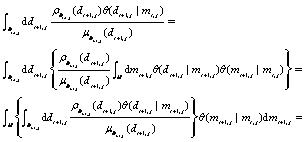
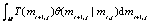                    (10)

where  θ(m_i+1,j|m_i,j), represents the conditional probability of the information transfer between the nearest neighbor pixel (i,j) and (i+1,j). Assume θ(m_i+1,j|m_i,j) is Gaussian distribution, then we have

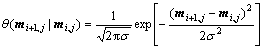   (11)

where  σ is a parameter to determine the effect of neighboring pixel (i+1, j).

The latter three integral terms have the similar expressions to the second integral term. Then Eqn.(8) can be written as follows:

σ_M(m_{i, j})=αexp[-S₂(m_{i, j})]R(m_{i, j})                 (12)

where

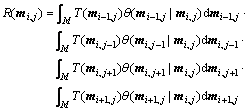
Apply logarithm to both sides of Eqn.(12), then

S₃(m_{i, j})=S₂(m_{i, j})-lnR(m_{i, j})                     (13)

Eqn.(13) is the cost function to retrieve the canopy biophysical variables at pixel (i, j) using spatial contextual information.

From Eqn.(11), the less the difference between the parameters m_{k, l} (|k-i|+|l-j|≤1) at the neighboring pixels and m_{i, j} at the current one is, the greater the value of the spatial information transfer function is, and the greater the influence from the neighbor pixels on the parameter retrieval at the pixel (i, j) is. When the spatial information transfer function θ(m_{i+1, j}|m_{i, j}) meets the uniform distribution, Eqn.(13) reduces to the cost function defined in Eqn.(6). In other words, there is no information from 4-neighbor pixels contributing to the parameter retrieval at pixel (i, j).

In order to test the above algorithm, the ETM+ reflectance data were used to retrieve LAI. The results were also compared with those from a conventional method.

3.1 Radiative transfer model and experimental data

Many canopy radiative transfer models have been developed to obtain land surface biophysical parameters. In parameter retrieval of this work, SAILH model, developed by VERHOEF^[17], was chosen as the forward model to simulate the canopy reflectance.

The main input parameters of the SAILH model are the canopy structure parameters and view geometry parameters. The canopy structure parameters include LAI, leaf angle distribution (LAD) function parameters (a and b) and hotspot-effect parameter, which represent the structural characteristics of canopy; leaf reflectance and leaf transmission which denote the spectrum characteristics of leaves; soil reflectance which denotes the spectrum characteristics of the background and SKYL which denotes the condition of the atmosphere. In the process of parameter retrieval, LAI is a free parameter and other parameters, determined according to the a prior information, are fixed. The solar zenith angle is calculated with ETM+ overpass. Since ETM+ observes at nadir, the view zenith angle is assumed to be 0?, and the relative azimuth angle is set to be an arbitrary value.

The satellite and ground measurement data provided by the MODIS validation team^[18] were used to validate the algorithm. Konza Prairie (96.56? W, 39.08? N), KS, USA was selected as the test site. This region is mainly covered by grass. ETM+ data, with spatial resolution of 25 m, acquired on Aug 13th, 2001, have been corrected atmospherically. The BIGFOOT project provides the retrieval LAI from the ETM+ data^[19]. Since the LAI provided by BIGFOOT has been validated with the ground measurements, it is taken as “true LAI” to compare with the results retrieved by the algorithm in this experiment.

3.2 Retrieval results

A prior information can be obtained from spectral library or many other means. In our retrieval, MODIS LAI products on August 13, 2001 were used as the prior information.

MODIS LAI products have spatial resolution of   1 km and adopt the projection of ISIN, while the ETM+ data adopt the projection of UTM WGS84. The general coordinate transformation package (GCTP) was used here to make a projection transition between the coordinates and the LAI products were resampled.

The false composition imagery from ETM+ bands 1, 2, and 4 is shown in Fig.2(a) and LAI mapping results retrieved from the ETM+ data are displayed in Fig.2(b). As can be seen, the spatial distribution of LAI values matches the pattern of false composition imagery very well and the range of LAI values is also reasonable.

Fig.2 LAI mapping results retrieved from ETM+ data: (a) ETM+ data (false composition imagery with bands 4, 2 and 1); (b) LAI retrieved from ETM+ data

To further confirm the validity of the algorithm, a small area of 8×8 is chosen from ETM+ image in which each pixel has the same land cover type. Fig.3 shows the retrieval results of each pixel in the area. Fig.3(a) shows the results that take into account the spatial information; Fig.3(b) shows the results of the conventional retrieval method. Associated statistics including correlation coefficient (R²) and root mean square error (E) are also presented in Fig.3. As can be seen, by introducing the spatial contextual information, the results with E=0.62 are much better than those estimated using conventional algorithm.

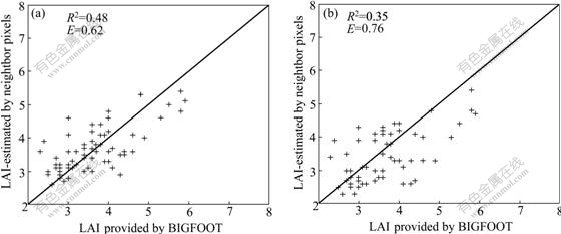
Fig.3 Scattered plots between true LAI and estimated LAI with prior information: (a) Retrieval LAI with spatial information;(b) Retrieval LAI without spatial information

4 Conclusions

1) A new algorithm using spatial contextual information is developed to estimate canopy biophysical variables from high-resolution remote sensing images. And the traditional retrieval cost function is just the special form of the cost function with the spatial contextual information.

2) Contextual information plays an important role in improving the retrieval performance. The experimental results show that proper utilization of spatial contextual information can improve the retrieval performance significantly compared with the conventional pixelwise retrieval.

3) The algorithm presented in this work just aims at the observational information at the 4-neighbor pixels, and further research will extend the neighborhood.

[1] DENG Ji-qiu, BAO Guang-shu. Analysis and design of information system of remote sensing integrated survey about land resources in Hunan province based on GIS [J]. Journal of Central South University of Technology: Science and Technology, 2003, 34(2): 192-195. (in Chinese)

[2] ZUO Ren-guang, XIA Qing-lin, TAN Ning, ZHENG You-ye. Synthetic information prediction of porphyry copper in Tibet [J]. Journal of Central South University: Science and Technology, 2007, 38(2): 368-373. (in Chinese)

[3] LIANG S L. Quantitative remote sensing of land surfaces [M]. New York: John Wiley, 2004: 246-301.

[4] WEISS M, BARET F. Evaluation of canopy biophysical variable retrieval performances from the accumulation of large swath satellite data [J]. Remote Sensing of Environment, 1999, 70(3): 293-306.

[5] KIMES D S, KNYAZIKHIN Y, PRIVETTE J L, ABUELGASIM A A, GAO F. Inversion methods for physically-based models [J]. Remote Sensing Review, 2000, 18(2/4): 381-440.

[6] MYNENI R B, RAMAKRISHNA R, NEMANI R, RUNNING S W. Estimation of global leaf area index and absorbed par using radiative transfer models[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(6): 1380-1393.

[7] FANG H, LIANG S, KUUSK A. Retrieving leaf area index using a genetic algorithm with a canopy radiative transfer model [J]. Remote Sensing of Environment, 2003, 85(3): 257-270.

[8] DANIEL T D, CHEN Z X, HWANG J N, TSANG L. Solving inverse problems by Bayesian iterative inversion of a forward model with applications to parameter mapping using SMMR remote sensing data [J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(5): 1182-1193.

[9] KITTLER J, FOGLEIN J. Contextual classification of multispectral pixel data [J]. Image and Vision Computing, 1984, 2(1): 13-29.

[10] TARANTOLA A. Inverse problem theory and methods for model parameter estimation [M]. Philadelphia: Society for Industrial and Applied Mathematics, 2004: 32-37.

[11] GEOL N S, STREBEL D E, Inversion of vegetation canopy reflectance models for estimating agronomic variables (I): Problem definition and initial results using the suits model [J]. Remote Sensing Environment, 1983, 13(6): 487-507.

[12] LIANG S L. Recent developments in estimating land surface biogeophysical variables from optical remote sensing [J]. Progress in Physical Geography, 2007, 31(5): 501-516.

[13] COMBAL B, BARET F, WEISS M, TRUBUIL A, MACE D, PRAGNERE A, MYNENI R, KNYAZIKHIN Y, WANG L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem [J]. Remote Sensing of Environment, 2003, 84(1): 1-15.

[14] VERSTRAETE M M, PINTY B, MYNENI R B. Potential and limitations of information extraction on the terrestrial biosphere from satellite remote sensing [J]. Remote Sensing of Environment, 1996, 58(2): 201-214.

[15] LI Xiao-wen, WANG Jin-di, HU Bao-xin, STRAHLER A H. On utilization of prior knowledge in inversion of remote sensing model [J]. Science in China (Series D), 1998, 41(6): 580-586.

[16] QU Yong-hua, WANG Jin-di, LIU Su-hong, WAN Hua-wei, ZHOU Hong-min, LIN Hao-bo. Study on hybrid inversion scheme under Bayesian network [J]. Journal of Remote Sensing, 2006, 10(1): 6-14. (in Chinese)

[17] VERHOEF W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model [J]. Remote Sensing of Environment, 1984, 16(2): 125-141.

[18] COHEN W B, MAIERPERGER T K, TURNER D P, RITTS W D, PFLUGMACHER D, KENNEDY R E, KIRSCHBAUM A, RUNNING S W, COSTA M, GOWER S T. MODIS land and LAI collection 4 product quality across nine sites in the western hemisphere [J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(7): 1843-1857.

[19] COHEN W B, MAIERPERGER T K, YANG Z, GOWER S T, TURNER D P, RITTS M, BERTERRETCHE M, RUNNING S W. Comparisons of land cover and LAI estimates derived from ETM+ and MODIS for four sites in North America: A quality assessment of 2000/2001 provisional MODIS products [J]. Remote Sensing of Environment, 2003, 88(3): 233-255.

Foundation item: Project(2007CB714407) supported by the Major State Basic Research and Development Program of China; Project(2004DFA06300) supported by Key International Collaboration Project in Science and Technology; Projects(40571107, 40701102) supported by the National Natural Science Foundation of China

Received date: 2008-03-20; Accepted date: 2008-06-10

Corresponding author: XIAO Zhi-qiang, PhD; Tel: +86-10-58807455-1433; E-mail: zhqxiao@bnu.edu.cn

(Edited by ZHAO Jun)