J. Cent. South Univ. (2020) 27: 963-972

DOI: https://doi.org/10.1007/s11771-020-4344-8

Dynamic response and failure of rock in initial gradient stress field under stress wave loading

WENG Lei(翁磊)¹, WU Qiu-hong(吴秋红)^{2, 3}, ZHAO Yan-lin(赵延林)^{2, 3}, WANG Shi-ming(王世鸣)⁴

1. School of Civil Engineering, Wuhan University, Wuhan 430072, China;

2. Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China;

3. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China;

4. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: Once an opening is created in deep underground, the stresses surrounding the opening will be redistributed, inducing a gradient stress field. To understand how the ground rock in such a gradient stress field responses to dynamic stress loading, the gradient stress distribution at a circular opening was first analyzed and the propagation of 1D stress wave in rock mass under gradient stress field was theoretically derived. By using an implicit to explicit solution method in LS-DYNA code, the dynamic mechanical behaviors of rock in gradient stress field were numerically investigated. The results indicate that the damage is mainly produced at or near the free face, partly due to the straight action of compressive stress wave and the tensile stress wave generated at the free face. The range of the induced damage zone is narrowed under the conditions of higher gradient stress rate and lower dynamic stress amplitude. However, under lower gradient stress field and higher dynamic stress, the damage becomes severer and wider with discontinuous failure regions.

Key words: deep opening; gradient stress rate (GSR); stress wave; damage zone; LS-DYNA

Cite this article as: WENG Lei, WU Qiu-hong, ZHAO Yan-lin, WANG Shi-ming. Dynamic response and failure of rock in initial gradient stress field under stress wave loading [J]. Journal of Central South University, 2020, 27(3): 963-972. DOI: https://doi.org/10.1007/s11771-020-4344-8.

1 Introduction

The stability of deep opening has long been a significant and challenging issue in the field of mining and civil engineering [1, 2]. For deep underground engineerings, dynamic stress wave is frequently generated in rock mass due to the drill-blast operation, microseismic events or other vibration sources. Stress wave propagation in initially stressed rock mass may degrade the mechanical properties, and hence cause instability of rock [3-5]. Researches on wave propagation in pre-stressed materials have been started long ago [6]. The effect of initial stress on the wave propagation has been theoretically explored by many scholars [7-10], and the results indicated that the initial stress does affect the wave propagation in solid materials. Meanwhile, laboratory experiments were conducted to investigate the relation of initial stress with the wave propagation and dynamic physical properties [11-15].

On the other hand, the failure mechanism of rock under initial stress and dynamic stress loading has been studied from both experiments and numerical simulations. For instance, LI et al [16] conducted laboratory experiments on rocks under coupled static and dynamic stresses using a modified split Hopkinson pressure bar (SHPB) apparatus. LI et al [17] investigated the dynamic response of highly-stressed pillars under the propagation of stress wave, and found that the influence of dynamic stress wave on the stability of the pillar becomes stronger with the increase of static prestress. ZHU et al [18] numerically simulated the rockburst mechanism of deep opening induced by dynamic disturbance, and found that the contribution of the dynamic loads is closely related to both static geo-stress waveforms and dynamic stress waveforms. However, the initial stress involved in the above works is homogeneous. In fact, the initial stress may not be homogeneous for rock mass occasionally. The seismic wave is a typical example of stress wave propagation in a medium with gravity gradient [19-21]. The stress gradient is generated due to the weight of the overlying rock mass and the tectonic stress. In addition, when an opening is excavated in rock mass, the induced stresses surrounding the opening are non-uniform. The new set of induced-stresses within the excavation disturbed zone varies gradually from surface to far field rock mass, forming a gradient stress field in the surrounding rock. However, little literature has been published concerning on the dynamic mechanical behaviors of rock mass in such a gradient stress field.

This paper aims to investigate the dynamic response and damage characteristics of ground rock in gradient stress field subjected to stress wave loading. The stress wave propagation in gradient stress field was first theoretically studied based on a simplified mechanical model. By using an implicit to explicit solution method, the stress and damage evolution of rock under gradient stress field and dynamic stress wave were numerically investigated. Finally, the effects of gradient stress and dynamic stress on the damage characteristics of the rock were studied.

The remaining of paper is organized as follows: Section 2 theoretically derives the control equations of stress wave propagation in gradient stress field; Section 3 introduces the setup of numerical simulation; the numerical results and analyses are presented in Section 4; conclusions are given in Section 5.

2 Theory of stress wave propagation in gradient stress field

2.1 Gradient stress field surrounding opening

Once an opening is created in rock mass, the in-situ stresses which existed before the excavations will redistribute and adjust to a new equilibrium, inducing inhomogeneous stresses at the periphery of the opening. The induced stresses are a function of the excavation shape and in-situ stresses [22-24]. For a circular or an elliptical opening, closed-form solutions of induced stresses and displacements can be theoretically derived, whereas the stress distributions around complex excavation shapes may be obtained either from closed form solutions for approximating simple shapes or by the use of computational procedures [25]. To simplify the problem, this study considers the induced radial stress surrounding a circular opening, and therefore the radial stress σ_rr, is given by:

 (1)

where p is the vertical field stress; K is the lateral pressure coefficient; is the scaled distance and can be given by =r/r_c, where r_c is the radius of the opening; r is the distance from the opening profile. Figure 1 gives the radial stress distributions around circular opening with different lateral pressure coefficients.

Figure 1 Distribution of radial stress around circular opening

Figure 1 indicates that significant disturbance of pre-excavation stresses is maintained within a near-field domain of five times radius of the opening (i.e. r≤5r_c). Alternatively, the state of stresses is not significantly different from far-field in-situ stresses when the location is beyond five times radius (r>5r_c). To better understand the gradient stress distribution at the near-field domain, a new indicator, namely gradient stress rate (GSR, r_g), is introduced to describe the change of the gradient stress per unit distance, and can be expressed as:

                             (2)

The distribution of the induced stresses around the opening is non-uniform and therefore, the GSR varies nonlinearly with the distance from the excavation profile. Eqs. (1) and (2) indicate that GSR exhibits a positive correlation with the initial vertical stress and lateral pressure coefficient, whereas it is negatively related to the radius of the opening.

2.2 Theoretical solutions of wave propagation in gradient stress field

A simplified mechanical model was built considering the problem as one-dimensional wave propagation in a long and slim rock rod with initial gradient stress applied to the radial orientation (see Figure 2). It should be noted that the rock rod is an incompressible material under excavating-induced stresses on most occasions of excavation projects. The left end was set as a free boundary representing the excavation profile, and the right hand end was fixed representing far field rock mass. For this scenario, a dynamic stress wave was applied on the left boundary of the rod.

The gradient stress distributes along the rod following the relationship as:

                               (3)

where S is gradient stress; X is the distance from the coordinate origin.

Consider a small element of length dX and let the cross-sectional area of the rod be A. Therefore,according to the Newton’s second law, the movement equation of the element is given by:

       (4)

where σ is the dynamic stress of wave on the face passing through AA′; ρ is the rock density; u is the displacement of the element. Eq. (4) can be simplified as:

                      (5)

The stress σ and the strain follows the relation:

                               (6)

where E is the elastic modulus. Substituting Eq. (6) to Eq. (5), it gives:

                    (7)

Eq. (7) is the governing equation of stress wave propagation in a gradient stress field, of which the term is GSR. Eq. (7) indicates that the waveform will be changed due to the existence of the gradient stress. The initial condition is:

                              (8)

The boundary condition for the problem is:

                          (9)

where l is the length of the rock road.

Figure 2 1D stress wave propagation in gradient stress field

Therefore, based on Eqs. (7)-(9), the propagation of stress wave can be calculated using mathematical physics method when the forms of gradient stress and dynamic stress wave are specified [19]. For instance, the dynamic response of rock subjected to a loading wave which has a function of can be derived. Figure 3 presents the displacement-time curves of the observation location (X=0) under varying GSRs. It is indicated in Figure 3 that when rock is free from gradient stress (i.e. r_g=0), the curve form of displacement against time is the same as the original waveform. However, the waveform changes with the GSR when the stress gradient is not equal to zero. It can be observed that the waveform for r_g=2.0 MPa/m is more complicated than that of r_g=1.0 MPa/m, and is far more different from the original waveform.

Figure 3 Variation of displacement vs. time at different GSRs (X=0)

Figure 4 shows the displacement-time curves at different locations under r_g=0, 1.0 and 2.0 MPa/m, respectively, which illustrates the changes in the amplitudes and waveforms of the rock at different locations. These findings indicate that the existence of gradient stress significantly influences the wave propagation, and thus induces different dynamic responses to rock. To further investigate the dynamic response and failure of rock under gradient stress field, numerical simulations were conducted in the following sections.

3 Numerical simulation setup

3.1 Implicit to explicit solution method

The problem of the stress wave propagation in initial gradient stress field, which involves two types of loading including initial gradient stress and dynamic stress wave, is a coupled static-dynamic loading problem. This problem can be solved following two steps for numerical calculation. The initial gradient stress state of the modelling is calculated in the first step, and then the dynamic loading process is computed on the basis of the static calculation data set. To this end, numerical code LS-DYNA has a good solution procedure, i.e. implicit to explicit solution method. An implicit module is called to calculate the initial gradient stress state, and the data of the element displacement and stress are output into a database file. Then the explicit module is used for further calculation of the mechanical responses with dynamic stress wave. In the explicit calculation stage, the database file containing the results of displacement and stress is imported into the model to update the geometry and the stress history of the elements so as to match the implicit solution results [26, 27].

Figure 4 Displacement-time curves at different locations under:

3.2 Gradient stress and dynamic stress wave

In Section 2.1, it is known that the gradient stress rate varies in a non-linear manner when increasing the distance from the excavation surface. As seen in Figure 1, the GSR is more sensitive to the change of the distance within three times radius of the opening than that in a far-filed domain. As a matter of fact, most rock failures, such as spalling or rockburst, occurred near the excavation surface where the gradient stress distribution is more significant. To make the problem simpler, this paper models the rock mass which is limited in three times radius region (i.e.), and assumes that the gradient stress in the region is distributed in a linear manner. Therefore, the average gradient stress rate in the domain of three times radius is given as:

                  (10)

It is observed that the gradient stress rate is independent to the opening’s radius, but is related to the vertical pressure and lateral pressure coefficient. Hence, according to Eq.(10), if the vertical pressure applied on the opening reaches 20 MPa, the gradient stress rate can be obtained as 5.9 MPa/m for lateral pressure coefficient K=1,10.8 MPa for K=2, and 15.8 MPa for K=3. In the model, three gradient stress rates of 5.9, 10.8 and 15.8 MPa/m were set up to study how they influence the dynamic responses of rock with initial gradient stress, respectively. Figure 5 shows the stress gradient distribution in the numerical model. Meanwhile, in the explicit calculation stage, a triangle stress wave with one peak was added on the model. The total action time of the stress wave was 4.0×10^-5 s, of which the rising time was 1.0×10^-5 s and the peak stress (P_tm) was 40 MPa, as seen in Figure 6.

Figure 5 Gradient stress distribution

Figure 6 Dynamic stress wave

3.3 Computational model and rock material

A rock rod with 3.0 m in length and 0.1 m in diameter was built in the code, as presented in Figure 7. The gradient stress distribution was achieved by applying acceleration to the x-direction. Convergence tests were carried out on the model to estimate the minimum required number of element for achieving stable and reliable simulation. Satisfied element size and proper element number were obtained when the difference between displacements for two consecutive element size was less than 5%. After convergence tests, the total number of the element used in the model was 37200 with an average size of 0.01 m.

Figure 7 Geometry and boundary conditions

It is known that rockburst or spalling is a typical brittle failure with steep stress drop after peak point in stress-strain curve. In this paper, a brittle damage material model was used in the code to simulate dynamic failure characteristics of hard brittle rock due to stress wave. The material model permits progressive degradation of tensile strength and shear strength across smeared cracks which are initiated by tensile loadings. The elastic modulus as input is an internal variable to consider the damage evolution governed by the maximum dissipation law, while the rate effect is modeled through setting certain viscous behavior of the material [28]. The feasibility of the model has been previously validated by comparing the stress-strain curves between experimental and numerical results [27,29]. Table 1 gives the parameters used in the brittle damage model. The velocity of the stress wave in the rock was calculated bym/s. The propagation time t for the wave travelling from right to left was obtained fromms. Therefore, the simulation time was set as 4t, i.e.approximate 3.0 ms, to give the stress wave sufficient time in propagating in the rock.

Table 1 Inputs in the rock model

4 Numerical simulation results and analyses

4.1 Stress wave propagation and damage evolution in gradient stress field

In the implicit calculation stage, certain acceleration is added on the model in order to generate initial gradient stress state in the rock. By applying an acceleration of 4000.0 m/s² to the x-direction of the model, the desired gradient stress distribution with gradient stress rate of 10.8 MPa/m can be obtained. Figure 8 shows the initial gradient stress and stress wave propagation process under r_g=10.8 MPa/m. Prior to the stress wave loading, it is seen that the initial stress is gradually increased from the free face to the fixed boundary. Once a compressive stress wave is generated at the free face, the stress wave propagates towards the fixed side (Figure 8(b)). When t=0.735 ms, the stress wave reflects at the fixed boundary and then moves back in a compressive waveform having twice the amplitude of the initial incident wave (Figure 8(c)). As the reflected compressive wave arrives at the free face, it reflects again and shifts its waveform into a tensile style (Figure 8(d)). The reflected tensile wave continues propagating and reflecting repeatedly whenever it meets the boundaries.

Figure 8 Simulation result of stress wave propagation in gradient stress field

Because of the damping effect of rock, the stress wave keeps attenuating and will eventually cease to propagate. Alternatively, the calculation will get to convergence after several times wave reflections in the model.

Figure 9 presents the stress histories of three special elements located at the free end (A), middle (B) and fixed end (C), respectively. The waveforms are also annotated in Figure 9. It is observed that the rock elements at different locations exhibit distinct responses upon the stress wave loading. For instance, the stress amplitude of the free end is larger than that of middle, whereas both of their amplitudes are much lower than that of the fixed end. This is due to a fact that compressive wave overlaps the reflected compressive wave at the fixed end, causing its amplitude to be greater than that of the compressive stress wave prior to reflection. On the other hand, when the compressive wave reflects at the free face, the wave will change into a tensile fashion, and therefore the compressive and the tensile waves overlap at the free face. During the process of wave propagation, if the compressive stress of the rock element reaches its yield limit, the rock element will experience plastic deformation to failure. Otherwise, the rock element will be damaged in tensile manner when the tensile stress exceeds its tensile limit.

Figure 9 Stress history curves of elements at free end, middle and fixed end

Figure 10 demonstrates the damage evolution process of the rock in the gradient stress field. It is seen that the damage is mainly generated at or near the free face. Part of the damage zone is induced by the straight action of compressive stress wave, while other damage is caused by the tensile wave generated in the rock rod.

Figure 10 Damage evolution process in gradient stress field with r_g=10.8 MPa/m

4.2 Influences of initial GSR and stress wave amplitude on the damage zone

By applying accelerations of 2185.2 and 5851.6 m/s² to the x-direction on the model, the gradient stress rates of 5.9 and 15.8 MPa/m can be achieved, respectively. In this section, additional simulations were conducted with varying GSRs and identical dynamic stress wave to investigate how the initial gradient stress rate influences the damage characteristics. Figure 11 presents the simulation results of damage zone of the rock under different GSRs. It is indicated that the damage zone is narrowed as the magnitude of the GSR increases. Furthermore, the damage zone is non-continuous amongst with two small elastic regions for the occasion when the GSR is as low as 5.9 MPa/m. This phenomenon is illustrated in the following.

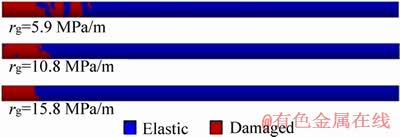
Figure 11 Damage zone of rock with different gradient stress rate

In addition, the effect of stress wave amplitude on the damage characteristics is also considered. The stress wave applied on the model has the same loading time but different amplitudes. Three amplitudes of 40, 60 and 80 MPa of the stress wave were applied to the model with an identical GSR of 10.8 MPa/m, respectively. Figure 12 presents the damage zone of the rock under different stress wave amplitudes. It is seen that with the increase in the stress wave amplitude, the damage becomes severer with wider region. Similarly, discontinuous damage zones are generated in the rock under higher stress wave amplitude.

Figure 12 Damage zone of rock with different stress wave amplitudes

The above simulation results indicate that with certain gradient stress and dynamic stress loading condition, the discontinuous damage phenomenon may occur in rock mass around the opening profile. Substantial field observations on the zonal disintegration phenomenon in mines [30-32] have similar failure zones to the results from the numerical simulations.In practice, the excavating- induced stresses around the opening are heterogeneous, offering the condition of gradient stress field, while drill-blast operation in the aim of advancing the opening gives the latter condition of stress wave loading. In this paper, as illustrated in Section 4.1, the damage zone at the free face is induced by the compressive stress wave at first, whereas the later-generated damages are caused by tensile stress wave. Due to the combined actions of the gradient stress and stress wave having a proper proportion, the discontinuous damage zones may be produced in one round of drill-blast operation.

In terms of traditional knowledge, the generation of the discontinuous damage zones should be avoided in practical engineering project. However, for mining at depth where more damages are acceptable or favored for extracting orebody mass, optional blast scheme can be scheduled to obtain desired damage effect, as well as to reduce the rounds. For instance, in high gradient stress field, more explosive is needed to produce higher stress wave that can induce more damage zones. In low gradient field, the explosive amount can be saved with the generation of wide discontinuous damage zones.

5 Conclusions

The gradient stress field surrounding underground opening was analyzed. A simplified model was then built to illustrate the problem of stress wave propagation in gradient stress field. The damage evolution process was numerically simulated to further explore the dynamic response of rock in gradient stress field to dynamic stress. It was found that the damage zone at the free face is narrowed under higher gradient stress rate and lower dynamic stress amplitude. On the contrary, severer and wider damage zones with discontinuous failure regions will be induced in the rock under lower gradient stress rate and high dynamic stress amplitude. The findings in this paper are beneficial for designing appropriate blast scheme in deep mines, particularly in which more damage or fracture are demanded.

References

[1] WANG Shao-feng, LI Xi-bing, DU Ku, WANG Shan-yong, TAO Ming. Experimental study of the triaxial strength properties of hollow cylindrical granite specimens under coupled external and internal confining stresses [J]. Rock Mechanics and Rock Engineering, 2018, 51: 2015-2031. DOI: 10.1007/s00603-018-1452-y.

[2] WU Qiu-hong, WENG Lei, ZHAO Yan-lin, GUO Bao-hua, LUO Tao. On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates [J]. Engineering Geology, 2019, 253: 94-110. DOI: 10.1016/j.enggeo.2019.03.014.

[3] LIN Hai, DENG Jin-geng, LIU Wei, XIE Tao, XU Jie, LIU Hai-long. Numerical simulation of hydraulic fracture propagation in weakly consolidated sandstone reservoirs [J]. Journal of Central South University, 2018, 25: 2944-2952. DOI: 10.1007/s11771-018-3964-8.

[4] WANG Dong-yi, LI Xi-bing, PENG Kang, MA Chun-de, ZHANG Zhen-yu, LIU Xiao-qian. Geotechnical characterization of red shale and its indication for ground control in deep underground mining [J]. Journal of Central South University, 2018, 25(12): 2979-2991. DOI: 10.1007/ s11771-018-3968-4.

[5] LI He, SHI Shi-liang, LIN Bai-quan, LU Jie-xin, YE Qing, LU Yi, WANG Zheng, HONG Yi-du, ZHU Xiang-nan. Effects of microwave-assisted pyrolysis on the microstructure of bituminous coals [J]. Energy, 2019, 187: 115986. DOI: 10.1016/j.energy.2019.115986.

[6] TOLSTOY I. On elastic-waves in prestressed solids [J]. Journal of Geophysical Research, 1982, 87: 6823-6827. DOI: 10.1029/JB087iB08p06823.

[7] OGDEN R W, SOTIROPOULOS D A. The effect of pre-stress on the propagation and reflection of plane waves in incompressible elastic solids [J]. IMA Journal of Applied Mathematics, 1997, 59: 95-121. DOI: 10.1093/imamat/ 59.1.95.

[8] OGDEN R W, SINGH B. The effect of rotation and initial stress on the propagation of waves in a transversely isotropic elastic solid [J]. Wave Motion, 2014, 51: 1108-1126. DOI: 10.1016/j.wavemoti.2014.05.004.

[9] DHUA S, CHATTOPADHYAY A. Torsional wave in an initially stressed layer lying between two inhomogeneous media [J]. Meccanica, 2015, 50: 1775-1789. DOI: 10.1007/ s11012-015-0119-y.

[10] WU Qiu-hong, CHEN Lu, SHEN Bao-tang, DLAMINI B, LI Shu-qing, ZHU Yong-jian. Experimental investigation on rockbolt performance under the tension load [J]. Rock Mechanics and Rock Engineering, 2019, 52: 4605-4618. DOI: 10.1007/s00603-019-01845-1.

[11] WANG Qian, JI Shao-cheng, SUN Sheng-si, MARCOTTE D. Correlations between compressional and shear wave velocities and corresponding Poisson’s ratios for some common rocks and sulfide ores [J]. Tectonophysics, 20019, 469: 61-72. DOI: 10.1016/j.tecto.2009.01.025.

[12] ASEF M R, NAJIBI A R. The effect of confining pressure on elastic wave velocities and dynamic to static Young’s modulus ratio [J]. Geophysics, 2013, 78: D135-D142. DOI: 10.1190/geo2012-0279.1.

[13] LI Xi-bing, TAO Ming. The influence of initial stress on wave propagation and dynamic elastic coefficients [J]. Geomechanics and Engineering, 2015, 8: 377-390. DOI: 10.12989/gae.2015.8.3.377.

[14] ABDOLLAHIPOUR A, SOLTANIAN H, POURMAZAHERI Y, KAZEMZADEH E, FATEHI-MARJI M. Sensitivity analysis of geomechanical parameters affecting a wellbore stability [J]. Journal of Central South University, 2019, 26(3): 768-778. DOI: 10.1007/s11771- 019-4046-2.

[15] SUN Hong-xin, ZUO Lei, WANG Xiu-yong, PENG Jian, WANG Wen-xin. Exact H-2 optimal solutions to inerter-based isolation systems for building structures [J]. Structural Control and Health Monitoring, 2019, 26(6): e2357. DOI: 10.1002/stc.2357.

[16] LI Xi-bing, ZHOU Zi-long, LOK T S, HONG Liang, YIN Tu-bing. Innovative testing technique of rock subjected to coupled static and dynamic loads [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45: 739-748. DOI: 10.1016/j.ijrmms.2007.08.013.

[17] LI Xi-bing, LI Di-yuan, GUO Lei, YE Zhou-yuan. Study on mechanical response of highly-stressed pillars in deep mining under dynamic disturbance [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26: 922-929. DOI: 10.1016/S1872-2067(07)60020-5.

[18] ZHU Wan-cheng, LI Zhan-hai, ZHU Liang, TANG Chun-an. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance [J]. Tunnelling and Underground Space Technology, 2010, 25: 587-599. DOI: 10.1016/j.tust.2010.04.004.

[19] TAO Ming, CHEN Zheng-hong, LI Xi-bing, ZHAO Hua-tao, YIN Tu-bing. Theoretical and numerical analysis of the influence of initial stress gradient on wave propagations [J]. Geomechanics and Engineering, 2016, 10: 285-296. DOI: 10.12989/gae.2016.10.3.285.

[20] WU Qiu-hong, LI Xi-bing, WENG Lei, LI Qing-feng, ZHU Yong-jian, LUO Rong. Experimental investigation of the dynamic response of prestressed rockbolt by using an SHPB-based rockbolt test system [J]. Tunnelling and Underground Space Technology, 2019, 93: 103088. DOI: 10.1016/j.tust.2019.103088.

[21] JIANG Li-shuai, KONG Peng, ZHANG Pei-peng, SHU Jia-ming, WANG Qing-biao, CHEN Lian-jun, WU Quan-lin. Dynamic analysis of the rock burst potential of a longwall panel intersecting with a fault [J]. Rock Mechanics and Rock Engineering. DOI: 10.1007/s00603-019-02004-2. (in Press)

[22] GONG Feng-qiang, LUO Yong, LI Xi-bing, SI Xue-feng, TAO Ming. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels [J]. Tunnelling and Underground Space Technology, 2018, 81: 413-427. DOI: 10.1016/j.tust.2018.07.035.

[23] FENG Fan, LI Xi-bing, ROSTAMI J, PENG Ding-xiao, LI Di-yuan, DU Kun. Numerical investigation of hard rock strength and fracturing under polyaxial compression based on mogi-coulomb failure criterion [J]. International Journal of Geomechanics, 2019, 19(4): 04019005. DOI: 10.1061/(Asce)Gm.1943-5622.0001352.

[24] GONG Feng-qiang, SI Xue-feng, LI Xi-bing, WANG Shan-yong. Experimental investigation of strain rockburst in circular caverns under deep three-dimensional high-stress conditions [J]. Rock Mechanics and Rock Engineering, 2019, 52: 1459-1474. DOI: 10.1007/s00603-018-1660-5.

[25] FENG Fan, CHEN Shao-jie, LI Di-yuan, HU Song-tao, HUANG Wan-peng, LI Bo. Analysis of fractures of a hard rock specimen via unloading of central hole with different sectional shapes [J]. Energy Science and Engineering, 2019, 7: 2265-2286. DOI: 10.1002/ese3.432.

[26] LI Xi-bing, WENG Lei. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance [J]. Tunnelling and Underground Space Technology, 2016, 54: 61-72.

[27] WENG Lei, HUANG Lin-qi, TAHERI A, LI Xi-bing. Rockburst characteristics and numerical simulation based on a strain energy density index: A case study of a roadway in Linglong gold mine, China [J]. Tunnelling and Underground Space Technology, 2019, 69: 223-232. DOI: 10.1016/ j.tust.2017.05.011.

[28] GOVINDJEE S, KAY G J, SIMO J C. Anisotropic modeling and numerical-simulation of brittle damage in concrete [J]. International Journal for Numerical Methods in Engineering, 1995, 38: 3611-3633. DOI:10.1002/nme.1620382105.

[29] WENG Lei, LI Xi-bing, TAO Ming. Influence of geostress orientation on fracture response of deep underground cavity subjected to dynamic loading [J]. Shock and Vibration, 2015, 2015: 575879. DOI: 10.1155/2015/575879.

[30] ADAMS G R, JAGER A J. Petroscopic observations of rock fracturing ahead of stope faces in deep-level gold-mines [J]. Journal of the South African Institute of Mining and Metallurgy, 1980, 80: 204-209.

[31] SHEMYAKIN E I, FISENKO G L, KURLENYA M V, OPARIN V N, REVA V N, GLUSHIKHIN F P, ROZENBAUM M A, TROPP E A, KUZNETSOV Y S. Zonal disintegration of rocks around underground workings, Part 1: Data of in situ observations [J]. Soviet Mining Science Ussr, 1986, 22: 157-168. DOI: 10.1007/ BF02500863.

[32] QIAN Qi-hu, ZHOU Xiao-ping, YANG Hai-qing, ZHANG Yong-xin, LI Xue-hua. Zonal disintegration of surrounding rock mass around the diversion tunnels in Jinping II Hydropower Station, Southwestern China [J]. Theoretical and Applied Fracture Mechanics, 2009, 51: 129-138. DOI: 10.1016/j.tafmec.2009.04.006.

(Edited by ZHENG Yu-tong)

中文导读

应力波加载下含梯度应力场岩体的动力响应与破坏特征

摘要：深部岩体开挖后，受应力重分布的影响，临空面附近的岩体处于梯度应力状态。为研究含梯度应力场岩体的动态力学响应特征，首先对圆形硐室的梯度应力分布规律进行分析，从理论上推导出梯度应力场岩体在一维应力波作用下的波动方程。通过LS-DYNA程序的隐式-显式连续计算方法，对梯度应力场岩体的动力响应行为进行模拟研究。结果表明，在岩体受压缩应力波和反射拉伸波共同作用下，岩体的损伤主要发生在自由面附近。数值模拟结果表明，更高的应力梯度率以及更小的应力波幅值导致损伤区范围更小。然而，在较小的梯度应力场以及较强的应力波加载下，岩体损伤更严重，范围更广，并且会产生非连续破坏的现象。

关键词：深部开挖；梯度应力率；应力波；损伤区；LS-DYNA

Foundation item: Projects(51904101, 51774131, 51604109) supported by the National Natural Science Foundation of China; Project(2017M622524) supported by the Postdoctoral Science Foundation of China

Received date: 2019-09-18; Accepted date: 2019-11-13

Corresponding author: WU Qiu-hong, PhD, Associate Professor; Tel: +86-15974135618; E-mail: qiuhong.wu@hnust.edu.cn; ORCID: 0000-0002-7223-1495