Trans. Nonferrous Met. Soc. China 30(2020) 2812-2822

Kinetic mechanism of magnesium production by silicothermic reduction of CaO·MgO in vacuum

Yu-si CHE^1,2, Geng-peng MAI¹, Shao-long LI¹, Ji-lin HE^1,2, Jian-xun SONG¹, Jian-hong YI³

1. Henan Province Industrial Technology Research Institute of Resources and Materials, Zhengzhou University, Zhengzhou 450001, China;

2. School of Material Science and Engineering, Zhengzhou University, Zhengzhou 450001, China;

3. Faculty of Materials and Engineering, Kunming University of Science and Technology, Kunming 650093, China

Received 8 October 2019; accepted 20 August 2020

Abstract: The investigation of silicothermic reduction of CaO·MgO was carried out using a self-developed thermogravimetric analysis (TGA) instrument under vacuum and high temperature conditions. The TG data of pellets prepared with calcined dolomite, ferrosilicon and fluorite were determined at the heating rates of 1.5, 2.0, 2.5 and 3.0 °C/min in 5 Pa vacuum at 300-1400 °C, respectively. Model-free analysis and model-based analysis were applied for simulating the kinetic mechanism. By analyzing the characteristics of the initial and final reaction temperatures of TG curve, ratio of half-width of derivative TG curve and kinetic parameters, a conclusion was made that the most probable mechanism function is the first order formal chemical reaction with activation energy of 233.42 kJ/mol and pre-exponential factor of 5.14×10¹⁰ s^-1. This study provides the basic data of dynamics of silicothermic magnesium production under vacuum conditions.

Key words: magnesium production; non-isothermal kinetics; iso-conversional method; kinetic mechanism

1 Introduction

Low-density, high-specific strength, high- specific rigidity, and high electromagnetic shielding performance, make magnesium alloys potential candidates with extensive utilization in aerospace, automotive, electronics communications, biomedical materials [1], and energy storage materials fields [2]; moreover, these alloys have been hailed as “green engineering metal material in 2lst century” [3-7]. The process of magnesium production mainly includes electrolysis and thermal reduction. Since 2006, about 80% of primary magnesium of the world has been generated in China by the Pidgeon process [8,9]. The Pidgeon process is a thermal reduction process which extracts magnesium from pellets with peach pit shape. These pellets are prepared using calcined dolomite, ferrosilicon, and calcium fluoride under the molding pressure of about 150 MPa. In pellet, the calcined dolomite is used as a raw material, 75# ferrosilicon as a reducing agent, and calcium fluoride as a mineralizer. They react chemically in one horizontal reduction tank made of a heat- resistant steel under the vacuum pressures of 10- 30 Pa and temperatures of 1200-1230 °C [10-12].

Till date, some research efforts have been devoted to the study of the kinetics mechanism of magnesium production by silicothermic reduction under vacuum via various methods. For example, WYNNYCKYJ et al [13] analyzed the experimental data and developed a two-component model, wherein the chemical reaction rate was described in terms of the Jander equation and the latter was coupled with a slow heat transfer step. This model offered good potential to predict experimental rates and to account for the observed dependence of rate on reactant particle size, briquette size and calcined dolomite properties. XU and YUAN [14] presented shrinking unreacted core model with quasi interfacial reaction (macroscopic dynamic model) by analyzing experimental results, and derived a comprehensive rate equation controlled by pore diffusion of magnesium and quasi-interfacial chemical reaction. The equation was good to verify the reaction results when the conversion rate was from 30% to 80%. LI et al [15] studied the process of silicothermic reduction to magnesium in single pellet and analyzed the kinetics at different temperatures. The results indicated that the magnesium reduction reaction was controlled by the phase interface model and the diffusion model to an extent. ZHANG et al [16] reported an experimental study on the intrinsic chemical dynamics mechanism of the silicothermic reduction process, and developed a single uniform chemical reaction model, which was in good agreement with Arrhenius’ equation. The equation of the uniform chemical reaction model was represented by 1-(1-α)^1/3=k₀τexp[-E/(RT)] in the temperature range of 1000-1200 °C, and the apparent activation energy was a function of reaction time.

The kinetics of magnesium production by silicothermic reduction in vacuum was studied by isothermal method. However, non-isothermal method is more advantageous for solving kinetics. COATS and REDFERN [17] summarized advantages of determining kinetic parameters by thermogravimetric methods as follows: (1) considerably less data are required, (2) the kinetics could be probed over an entire temperature range in a continuous manner, and (3) when a sample undergoes considerable reaction at the required temperature, the results obtained by an isothermal method are questionable. However, it is well known that thermal analysis instruments, such as Netzsch and Mettler Toledo, are unable to test thermal analysis characteristics under vacuum and high temperature conditions, and the magnesium vapor generated during the reduction process can simultaneously pollute the instrument, which prevents the successful occurrence of magnesium production experiment. Thus, studies on non-isothermal method have not yet investigated the kinetics of magnesium production with silicothermic process in vacuum.

In this study, an experiment on magnesium production by silicothermic reduction in vacuum was conducted using a thermogravimetry analysis (TGA) instrument developed by our team. The non-isothermal method was applied for collecting the mass loss data, and model-free analysis and model-based analysis were employed to study the kinetics mechanism of magnesium oxide reduction.

2 Experimental

The raw materials including calcined dolomite (CaO·MgO), 75% ferrosilicon alloy (Fe·Si), and fluorite (CaF₂) used herein were in accordance with industrial production by Pidgeon process. The pellets used in experiment were obtained from a magnesium production plant in China, which adopted Pidgeon process to produce primary magnesium. The process mainly includes three steps: pellet preparation process, reduction process and refining process, as shown in Fig. 1.

Pellets for Pidgeon process were compressed using twinroller machine with size of 47 mm × 25 mm × 20 mm to a peach pit shape. Comparative analysis of density of pellets prepared by molding and that of pellets prepared by pressing indicated that the pressure of pellet was around 150 MPa. The raw material mixture ratio of pellet was based on a rule that the molar ratio of Si to 2MgO was 1.2 and the fluorite mass fraction was 3%. The chemical compositions of various materials for preparing pellets were tested, which are listed in Table 1.

The key equipment used in the experiment was TGA instrument developed by our team, and it was applied for testing the mass loss of pellets under vacuum and high temperatures with different heating rates. The pellets could react chemically as

Schematic illustration and photographs of TGA instrument are shown in Fig. 2. The corundum tube was placed vertically in the middle of furnace body heated with a silicon molybdenum rod. The weighing system was installed on the top of corundum tube, and the vacuum system was situated at the bottom of tube. Crucible connected to the weighing cell by a metal wire was placed in the middle of the heating area. The upper and lower sides of the crucible were insulated with porous alumina.

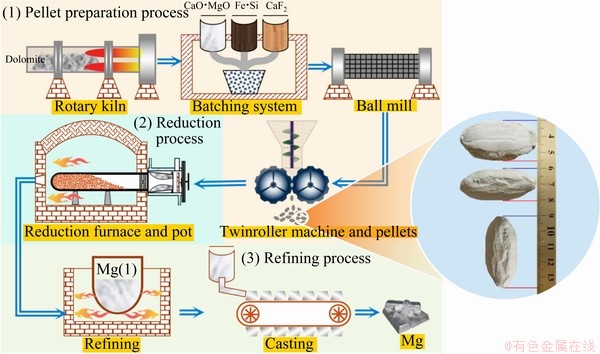
Fig. 1 Schematic of Pidgeon process (Three steps: preparation process, reduction process, and refining process) and pellet size

Table 1 Composition and calcining index of calcined dolomite (wt.%)

Fig. 2 Schematic illustration and photograph of TGA instrument developed by our team

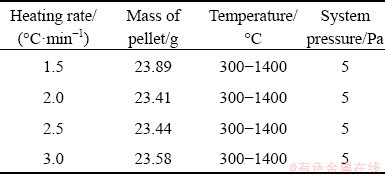
First, the weighing sensor and crucible were hung vertically from the top of the furnace, and the weighed pellets were placed into the crucible. Next, the weighing sensor, crucible, and pellet were relocated into the instrument tube. The corundum tube was sealed and purified three times with argon. It was vacuumed, the system pressure in the tube was stabilized at about 5 Pa, and the indicator value of the weighing sensor was set as 0. Then, the experiment was carried out following the setting up heating program. The chemical reaction characteristic of pellets was determined from 300 to 1400 °C at the heating rates of 1.5, 2.0, 2.5, and 3.0 °C/min, respectively. Some experimental parameters and mass of samples are listed in Table 2.

Table 2 Experimental parameters

In fact, the magnesium vapor, sodium vapor, and potassium vapor could be reduced from their oxides by silicon during the entire heating process; however, the reaction temperatures were different. Sodium and potassium vapors were produced before magnesium vapor. Only the mass loss curves due to vapor formation of magnesium were selected to carry out kinetics calculation. Moreover, formation of sodium and potassium vapors did not affect the data collection of magnesium mass and magnesium conversion. Furthermore, the dust and CaF₂ did not affect the mass loss of pellet in the reduction process of magnesium oxide. First, the dust that adhered to the surface of the pellets was found to be adverse for industrial production, for example, it increased the viscosity of reduced slag and generated impurities in crystalline magnesium. However, it was different from industrial production, the pellet used in experiment was a single one that had no dust on its surface, and the dust did not float under vacuum and high temperatures. Second, the melting point and boiling point of CaF₂ are 1418 and 2534 °C, respectively, and it does not sublime in experimental temperature range.

In this study, the reduction process of magnesium oxide at high temperatures was studied, and in this temperature range, pellet did not experience any reaction and sublimation except Reaction . Thus, the reduction rate could be calculated according to the initial and final points of reaction. On TG curves, the position where the mass started to reduce was the initial point of reaction and the point where it stopped changing was the final point of reduction reaction. The curve between initial point and final point denotes the conversion (α) of magnesia reduction, and the conversion of reaction was 0 at the starting point and 100% at the final point. The conversion corresponds to the degree of pellet reduction, which is defined as follows:

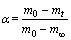
where m₀, m_t and m_∞ represent the initial mass of the pellet, the mass of the pellet at a specific time t, and the mass of the pellet at the end of reaction, respectively.

3 Results and discussion

3.1 Thermogravimetric analysis

Figure 3 plots the collection data. Figure 3(a) shows that the raw data obtained from thermogravimetry analysis instrument are not very stable. Apparently, data were just oscillated regularly and periodically. Thus, the raw data were processed with LOWESS function by using Origin software, and the processed results are presented in Fig. 3(b). In Fig. 3(b), the single obvious mass loss event on every TG curve after 1050 °C indicates the occurrence of chemical Reaction (1) in the heating process of pellets. TG curve reaches a plateau basically below 1050 °C, which illustrates the absence of any chemical reaction in the range of 300-1050 °C. Simultaneously, the results exhibit that the initial and final temperatures of chemical reaction are about 1050 and 1350 °C, respectively. The only mass loss event at different heating rates was plotted by mass loss rate as shown in Fig. 3(c). Translating the mass loss rate data to conversion shown in Fig. 3(d), so that the kinetics of chemical reaction could be conveniently simulated. The curves in the figure belong to classic deceleration model, where the reaction rate reaches the maximum at the initial stage of the reaction, and then decreases with increasing transformation degree. The most common example is the reaction series model.

3.2 Kinetics analysis and discussion

3.2.1 Model-free analysis

Model-free method is frequently titled as iso-conversional method. Owing to the temperature dependence on the iso-conversional rate, it can be used to evaluate iso-conversional values of the activation energy, without assuming or determining any particular form of the reaction model [18,19]. In general, analysis based on the following two assumptions is required for calculating the kinetics by model-free method. First, the reaction should always be described by only one kinetic equation for the conversion. Second, the conversion rate is considered as a function of temperature when conversion is a constant.

Fig. 3 TGA curves of pellet at heating rates of 1.5, 2.0, 2.5, and 3.0 °C/min, respectively

In this study, common and classic iso- conversional methods, namely, the Ozawa–Flynn–Wall (OFW) method and Kissinger–Akahira–Sunose (KAS) method were selected to compute and analyze the kinetics of magnesia reduction reaction. Friedman Method [20] is also a classic differential iso-conversional method, but the calculation is seriously influenced by baseline drift. Moreover, it is not possible to make the results either accurate or precise [21,22].

The OFW [23,24] analysis is the iso- conversional method which involves measuring the temperatures corresponding to fixed values of α from experiments at different heating rates (β). The plot between lg β and 1/T (T is the thermodynamic temperature) at different heating rates provides parallel line for conversion rate from 0 to 100%, and each conversion corresponds to the activation energy (E_a) from the slope of Eq. :

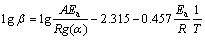
where β is the heating rate, g(α) is the assumption function, A is the pre-exponential, R is the molar gas constant. Based on Eq. , the curves of lg β against 1/T were plotted as shown in Fig. 4, where the slope is -0.457E_a/R.

The KAS [25,26] analysis is also an integral iso-conversional method, where the measurements are analyzed for multiple conversion levels. The determination of the activation energy uses the points at the same conversion from the measurements at different heating rates. The expression of KAS is represented as follows:

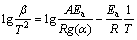
where E_a is assumed such that the activation energy depends on the degree of transformation.

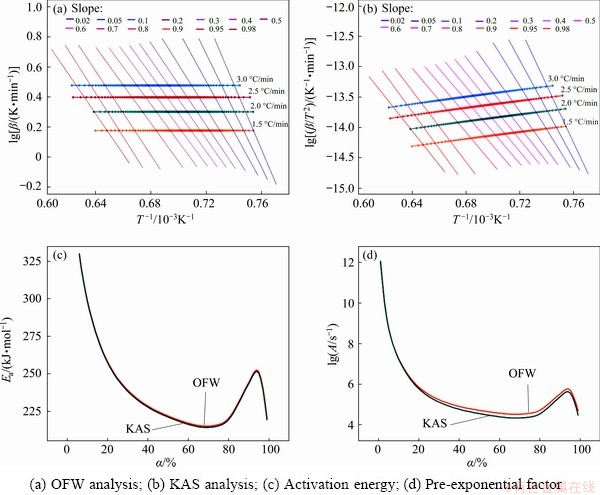
Fig. 4 Calculation and analysis of OFW method and KAS method

According to Eq. , the curve of lg(β/T²) vs 1/T was plotted in Fig. 4, where the slope gives –E_a/R, and R is 8.314 J/(mol·K).

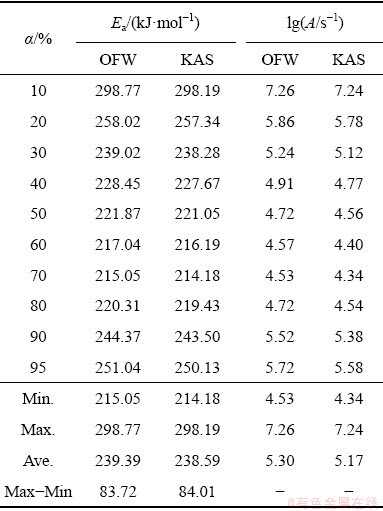
By calculation in a conversion range from 0 to 100%, the activation energy can be calculated by OFW method and KAS method, respectively. The results of calculation and analysis are shown in  Fig. 4, and data referring to activation energy and pre-exponential factor are listed in Table 3.

Figures 4(a) and (b) present the analysis process of model-free method of OFW and KAS, respectively. The two methods show the similar trends, and the slopes of the lines at iso-conversional points of the four curves maintain a certain value in conversion from 20% to 90%, and the slope changes obviously when conversion is below 20%. Figures 4(c) and (d) exhibit that the variation trends of activation energy and pre-exponential factor obtained by two methods are almost identical, and the kinetic parameters are very proximate.

Table 3 shows that the values of activation energies by OFW method are between 215.05 and 298.77 kJ/mol, and their average is 239.39 kJ/mol. Similarly, the values of activation energies by KAS method are between 214.18 and 298.19 kJ/mol, and the average value is 238.59 kJ/mol.

Comparative analysis of the results of the two calculation methods indicates that the activation energies are quite approximate. The difference between the maximum and the minimum of activation energies by the two methods are 83.72 and 84.01 kJ/mol, respectively, which are both much less than the average of activation energies. Thus, the kinetics parameters calculated by model-free method are credible [18].

3.2.2 Model-based analysis

Model-based analysis allows the solution of activation energy of the reaction process under the assumption of a known specific kinetic model.  The common solid-reaction kinetic mechanism functions were summarized in Refs. [27-29].

Table 3 Activation energy and pre-exponential factor by OFW method and KAS method

Magnesium oxide reduction via silicothermic reduction under vacuum is a type of solid-reaction. In general, the thermoanalytical kinetics of reactions during the TGA analysis is described by the non-isothermal kinetics (Eq. ) [30]:

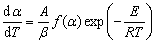
Integration of Eq. gives Eq. , and this process can be derived by three approaches of integration. The detailed derivation can refer to Refs. [31-33].

Simplification of Eq. (6) gives

The calculation was accomplished by the common functions of solid-reaction mechanisms under assumption that the reaction of pellet was a simple reaction. Based on the statistical criteria, the function that best approximates the experimental data was selected. The correlation values (R²) were greater than 0.99 as listed in Table 4.

Table 4 Calculation results of kinetics

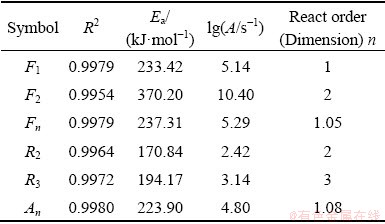
According to the kinetic parameters presented in Table 4 and Eq. , the fitted curves compared with experimental curves at different heating rates were plotted as Fig. 5.

Table 4 summarizes that there are six kinetic mechanism functions, including F₁, F₂, F_n, R₂, R₃, and A_n for which the correlation values (R²) are greater than 0.99. Figure 5 demonstrates that fitted curves of six mechanism functions all match well with experimental data. However, the activation energies of F₂, R₂, and R₃ (370.20, 170.84, and 194.17 kJ/mol) are out of the range between minimum and maximum (215.05-298.77 kJ/mol and 214.18-298.19 kJ/mol) calculated by the model-free method. Therefore, the three functions are not fit for describing the mechanism of  reaction.

DOLLIMORE et al [34] found that the mechanism could be determined by consideration of some parameters shown in Fig. 6 and Table 5 such as the character of TG curves at initial reaction temperature and final reaction temperature and the ratio of half-width on derivative TG (DTG) curves.

Figure 6(a) shows the schematic illustration for judging the character of the initial reaction temperature T_i as diffuse T_i-diffuse or sharp T_i-sharp and determination of the kinetic mechanism through the final reaction temperature T_f as T_f-diffuse or T_f-sharp on TG curves. Figure 6(b) presents the calculation of the ratio of left to right half-width taking the line through the peak point as the center axis on DTG curves to confirm the reaction type. The evidence supporting this judgement of the character of the initial and final reaction temperatures and the ratio of half-width are presented in Table 5.

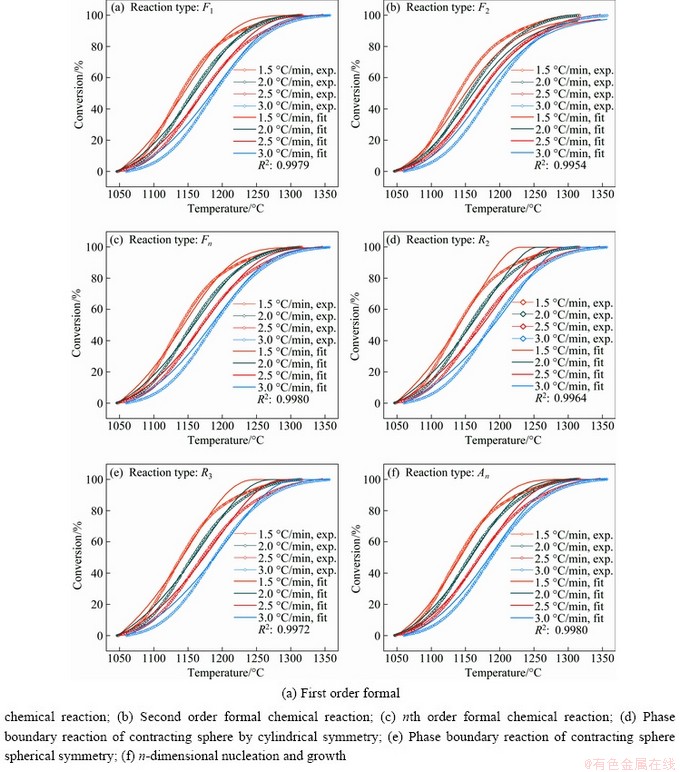
Fig. 5 Comparison of experimental and simulated values by different kinetics mechanism models

According to the method of determination of kinetic mechanism proposed by DOLLIMORE [34], the TG curve with heating rates of 2.5 and 3.0 °C/min were processed by differential method, and then the corresponding DTG curves were obtained. The ratios of half-width (δ_lo/δ_hi) were calculated as 0.76 and 0.79 from Figs. 7(a) and (b), respectively, and they all approach 1. Comparative analysis of data presented in Table 5 indicates that F₁, F₂, F_n and A_n reaction types are reasonable. Analysis of the mass loss curves shown in Fig. 7(c) indicates that the type of “diffuse” is according to the character of the initial and final reaction temperatures of all the TG curves. The character of the initial and final reaction temperatures of all the TG curves belongs to the type of “diffuse”.

Table 5 presents that the mechanism functions F₁, F₂, and F_n are selectable.

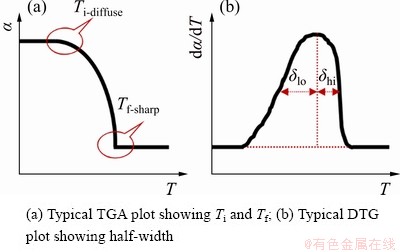
Fig. 6 Schematic representation showing characteristic parameters for determining reaction mechanism

Table 5 Characterization of kinetic mechanisms based on shape of TG plots

Combined with the previous analysis by comparing activation energies, mechanism functions F₁ and F_n meet all the judgement conditions, which verifies that the kinetic mechanism of magnesium oxide reduction by silicothermic reduction is a formal chemical reaction type. Values of reaction orders, activation energies and pre-exponential factor are all very close when the kinetic parameters of F₁ and F_n are compared, in particular, the reaction orders, the order for function F₁ equals 1, and it is 1.08 for function F_n. Moreover, the correlation values (R²) are also very close to each other. The final conclusion is that the first order formal chemical reaction is the most probable mechanism function of pellet reduction under vacuum and high temperatures.

Substituting E_a, A, and g(α) into Eq. gives

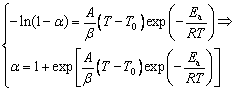
where T₀ is the initial temperature of the chemical reaction that can be obtained by turning points on TG curves.

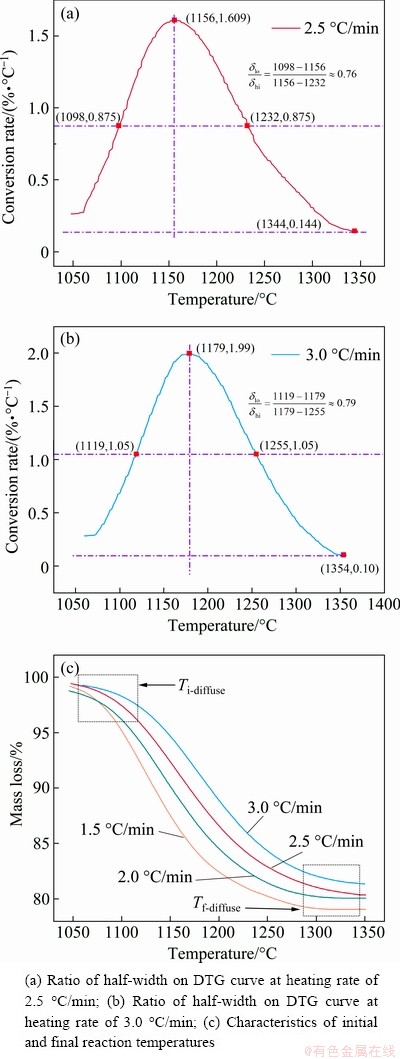
Fig. 7 Analysis and judgment of reaction mechanism

The above mentioned analysis indicates that the most probable mechanism function is the first order formal chemical reaction for the pellets undergoing a reduction reaction under vacuum, which also gives the best statistical fitting of experimental data, and the entire reaction process is perfectly described by Eq. . However, the best fitting of the kinetic data is not sufficient to draw reliable conclusions about the actual mechanism. Indeed, it has been shown that different reaction models provide very similar kinetics under constant heating conditions [35].

This study is different from previous related studies because of the different research methods used. In this study, the experimental data were collected using the TGA instrument developed by our team, and the kinetic mechanisms were computed by more credible non-isothermal method [17,36].

4 Conclusions

(1) The chemical reaction characteristics were investigated through the pellets used in the production of magnesium by Pidgeon process under high temperature and vacuum conditions for the first time. The mass loss data at different heating rates were collected using the self-made TGA instrument.

(2) Calculation results indicated that the most probable mechanism function is the first order formal chemical reaction, with the activation energy of 233.42 kJ/mol and pre-exponential factor of 5.14 × 10¹⁰ s^-1 for the chemical reaction occurring in pellets under vacuum.

(3) The results present the best statistical fit of kinetic mechanism and supplement the basic data of dynamics of silicothermic magnesium production, which provides a reliable dynamic model for the numerical simulation and optimization of magnesium production technology.

References

[1] CHU Cheng-lin, HAN Xiao, BAI Jing, XUE Feng, CHU Paul-kao. Surface modification of biomedical magnesium alloy wires by micro-arc oxidation [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(4): 1058-1064.

[2] ZHANG Yang-huan, LI Ya-qin, SHANG Hong-wei, HOU Zhong-hui, QI Yan, ZHAO Dong-liang. Electrochemical hydrogen storage performance of as-cast and as-spun RE-Mg-Ni-Co-Al-based alloys applied to Ni/MH battery [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(4): 711-721.

[3] EASTON M, BEER A, BARNETT M, DAVIES C, DUNLOP G, DURANDET Y, BLACKET S, HILDITCH T, BEGGS P. Magnesium alloy applications in automotive structures [J]. JOM, 2008, 60(11): 57-62.

[4] KULEKCI M K. Magnesium and its alloys applications in automotive industry [J]. International Journal of Advanced Manufacturing Technology, 2008, 39(9-10): 851-865.

[5] MORDIKE B L, EBERT T. Magnesium properties applications potential [J]. Materials Science and Engineering A, 2001, 302(1): 37-45.

[6] PAN Fu-sheng, ZHANG Jing, WANG Jing-feng, YANG Ming-bo, HAN En-hou, CHEN Rong-shi. Key R&D activities for development of new types of wrought magnesium alloys in China [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(7): 1249-1258.

[7] SUN Yue-hua, WANG Ri-chu, PENG Chao-qun, FENG Yan, YANG Ming. Recent progress in Mg-Li matrix composites [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(1): 1-14.

[8] DU Jin-dan, HAN Wei-jian, PENG Ying-hong. Life cycle greenhouse gases, energy and cost assessment of automobiles using magnesium from Chinese Pidgeon process [J]. Journal of Cleaner Production, 2010, 18 (2): 112-119.

[9] GAO Feng, NIE Zuo-ren, WANG Zhi-hong, GONG Xian-zheng, ZUO Tie-yong. Assessing environmental impact of magnesium production using Pidgeon process in China [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(3): 749-754.

[10] PIDGEON L M, KING J A. The vapour pressure of magnesium in the thermal reduction of MgO by ferrosilicon [J]. Discussions of the Faraday Society, 1948, 4: 197-206.

[11] TOGURI J M, PIDGEON L M. High-temperature studies of metallurgical processes: Part II. The thermal reduction of calcined dolomite with silicon [J]. Canadian Journal of Chemistry, 1962, 40(9): 1769-1776.

[12] XU Ri-yao. Magnesium production by siliconthermic reduction method [M]. Changsha: Central South University Press, 2003. (in Chinese)

[13] WYNNYCKYJ J R, RAO D B, MUELLER G S. Reaction kinetics in the silicothermic magnesium process [J]. Canadian Metallurgical Quarterly, 1977, 16(1): 73-81.

[14] XU Ri-yao, YUAN Hong-bo. Analysis of macro-kinetics model in magnesium production by silicothermic process [J]. Light Metal, 1991, 2: 39-44. (in Chinese)

[15] LI Rong-bin, ZHANG Chao, ZHANG Shao-jun, GUO Lie-jin. Experimental and numerical modeling studies on production of Mg by vacuum silicothermic reduction of CaO·MgO [J]. Metallurgical and Materials Transactions B, 2013, 45(1): 236-250.

[16] ZHANG Chao, CHU Hua-qiang, GU Ming-yan, ZHENG Shu. Experimental and numerical investigation of silicothermic reduction process with detailed chemical kinetics and thermal radiation [J]. Applied Thermal Engineering, 2018, 135: 454-462.

[17] COATS A W, REDFERN J P. Thermogravimetric analysis: A review [J]. Analyst, 1963, 88(1053): 906-924.

[18] VYAZOVKIN S, BURNHAM A K, CRIADO J M, PEREZ-MAQUEDA L A, POPESCU C, SBIRRAZZUOLI N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data [J]. Thermochimica Acta, 2011, 520(1-2): 1-19.

[19] FARJAS J, ROURA P. Isoconversional analysis of solid state transformations [J]. Journal of Thermal Analysis and Calorimetry, 2011, 105(3): 767-773.

[20] FRIEDMAN H L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry: Application to a phenolic plastic [J]. Journal of Polymer Science (Part C): Polymer Symposia, 1964, 6(1): 183-195.

[21] SBIRRAZZUOLI N. Is the Friedman method applicable to transformations with temperature dependent reaction heat [J]. Macromolecular Chemistry and Physics, 2007, 208(14): 1592-1597.

[22] BROWN M E, MACIEJEWSKI M, VYAZOVKIN S, NOMEN R, SEMPERE J, BURNHAM A, OPFERMANN J, STREY R, ANDERSON H L, KEMMLER A, KEULEERS R, JANSSENS J, DESSEYN H O, LI C R, TANG T B, RODUIT B, MALEK J, MITSUHASHI T. Computational aspects of kinetic analysis (Part A): The ICTAC kinetics project-data, methods and results [J]. Thermochimica Acta, 2000, 355(1): 125-143.

[23] OZAWA T. A new method of analyzing thermogravimetric data [J]. Bulletin of the Chemical Society of Japan, 1965, 38(11): 1881-1886.

[24] FLYNN J H, WALL LA. General treatment of the thermogravimetry of polymers [J]. Journal of Research of the National Bureau of Standards, 1966, 70: 487-490.

[25] KISSINGER H E. Variation of peak temperature with heating rate in differential thermal analysis [J]. Journal of Research of the National Bureau of Standards, 1956, 57: 217-221.

[26] AKAHIRA T, SUNOSE T. Joint convention of four electrical institutes [J]. Research Report Chiba Institute of Technology, 1971, 16: 22-31.

[27] HAN Yun-qing. Theoretical study of thermal analysis kinetics [D]. Ohio State: University of Kentucky, 2014: 91.

[28] VYAZOVKIN S, CHRISSAFIS K, DI LORENZO M L, KOGA N PIJOLAT M, RODUIT B, SBIRRAZZUOLI N, SUNOL J J. ICTAC kinetics committee recommendations for collecting experimental thermal analysis data for kinetic computations [J]. Thermochimica Acta, 2014, 590: 1-23.

[29] OCHOA A, IBARRA A, BILBAO J, ARANDES J M, CASTANO P. Assessment of thermogravimetric methods for calculating coke combustion-regeneration kinetics of deactivated catalyst [J]. Chemical Engineering Science, 2017, 171: 459-470.

[30] VYAZOVKIN S, WIGHT C A. Isothermal and non-isothermal kinetics of thermally stimulated reactions of solids [J]. International Reviews in Physical Chemistry, 1998, 17(3): 407-433.

[31] NORWISZ J. The kinetic equation under linear temperature increase conditions [J]. Thermochimica Acta, 1978, 25(1): 123-125.

[32] HU Rong-zu, YANG Zheng-quan, LIANG Yan-jun. The determination of the most probable mechanism function and three kinetic parameters of exothermic decomposition reaction of energetic materials by a single non-isothermal DSC curve [J]. Thermochimica Acta, 1988, 123: 135-151.

[33] BLAZEJOWSKI J. Evaluation of kinetic constants for the solid state reactions under linear temperature increase conditions [J]. Thermochimica Acta, 1981, 48(1): 109-124.

[34] DOLLIMORE D, TONG P, ALEXANDER K S. The kinetic interpretation of the decomposition of calcium carbonate by use of relationships other than the Arrhenius equation [J]. Thermochimica Acta, 1996, 282-283: 13-27.

[35] CRIADO J M, PeREZ-MAQUEDA L A. Sample controlled thermal analysis and kinetics [J]. Journal of Thermal Analysis and Calorimetry, 2005, 80(1): 27-33.

[36] JAIN A A, MEHRA A, RANADE V V. Processing of TGA data: Analysis of isoconversional and model fitting methods [J]. Fuel, 2016, 165: 490-498.

真空条件下硅热还原CaO·MgO冶炼金属镁的动力学机理

车玉思^1,2，买耕鹏¹，李少龙¹，何季麟^1,2，宋建勋¹，易健宏³

1. 郑州大学 河南省资源与材料工业技术研究院，郑州 450001；

2. 郑州大学 材料科学与工程学院，郑州 450001；

3. 昆明理工大学 材料与工程学院，昆明 650093

摘  要：采用自行研制的热重分析仪(TGA)，在真空和高温条件下对硅热还原CaO·MgO进行研究。采用1.5、2.0、2.5和3.0 °C/min升温速率分别测定由煅烧白云石、硅铁和萤石制成球团在5 Pa真空和300~1400 °C条件下的热重损失。选择无模式函数法与模式函数法对还原过程的动力学机理进行模拟计算，综合分析热重曲线在反应起始段与结束段的形状特性、微分热重的半宽比和动力学参数，最终得出还原反应的最概然机理函数是一阶化学反应模式函数，其活化能与指前因子分别为233.42 kJ/mol和5.14 × 10¹⁰ s^-1。该项研究工作为真空条件下硅热法炼镁提供了基础动力学数据。

关键词：镁冶炼；非等温动力学；等转化率法；动力学机理

(Edited by Xiang-qun LI)

Foundation item: Project (2016YFB0301100) supported by the National Key R&D Program of China; Project (51804277) supported by the National Natural Science Foundation of China; Project (2018ZE007) supported by the Rare and Precious Metal Materials Genome Engineering Project of Yunnan Province, China

Corresponding author: Ji-lin HE, E-mail: hejilin@zzu.edu.cn; Jian-xun SONG, E-mail: jianxun.song@zzu.edu.cn

DOI: 10.1016/S1003-6326(20)65423-1