基于块体理论的碎裂矿段底部结构空间的稳定性
来源期刊:中国有色金属学报(英文版)2016年第7期
论文作者:胡建华 杨春 周科平 李杰林 高峰
文章页码:1946 - 1954
关键词:楔体稳定性;碎裂矿段;底部结构;Unwedge软件;优化
Key words:wedge stability; fragment orebody; undercut; Unwedge software; optimization
摘 要:底部结构是地下矿山规模开采的重要工程结构和爆破补偿空间。在碎裂矿段的地下采矿过程中,对底部空间的块体结构和三维岩石楔体开展稳定性分析是采矿成功的关键。楔体的稳定性主要由地质因素(包括底部结 构与楔体的工程尺寸、形状和空间位置)、产生楔体结构的不连续面的剪切强度和抗拉强度以及岩体应力分布控制。应用Unwedge软件,设计横断面夹角、底部结构走向和倾角3因素、5水平的正交试验,获得底部结构的优化设计参数。研究结果表明:地下空间的安全系数为1.2,底部结构的参数优化由爆破块度、水流方向和设备爬坡能力决定;楔体的稳定性根据块体形状和连续冒落进行分析;优化参数为断面夹角27°、走向315°~325°、倾角5°,满足底部结构空间块体安全稳定性要求,是合理优化的设计参数。
Abstract: Undercut is one kind of important spaces to place the mining blocks in the mass underground mining. This structure is also used as a compensation space during blasting. In the process of underground mining in the fragment orebody, it is important and critical to analyze the stability and blockage of the three-dimensional wedges created around the undercut space. The wedge stability is mainly controlled by factors including geometry (i.e., the size, shape and spatial location of the wedge and undercut), the strength (shear and tensile) of the discontinuities that created the wedge, and the stress distribution within the rock mass. The Unwedge software was used to conduct the orthogonal simulation tests (three factors and five levels) that considered different cross sections, trends, and plunges of the undercut space. The results demonstrate that the control value of the safety factor of wedge is set to be 1.2. The optimal parameters are determined in the undercut space, such as the blasting fragmentation, orientation of the fluid flow, and the equipment gradeability; the wedge stability can be evaluated in the light of the block images and continuous falling; the stability of the key block meets the needs of the undercut space, the parameters gained are reasonable and optimal. Cross section is 27°, trend is from 315° to 325° (it is 320° at in-suit test) and plunge is 5°.
Trans. Nonferrous Met. Soc. China 26(2016) 1946-1954
Jian-hua HU1,2, Chun YANG1,2, Ke-ping ZHOU1,2, Jie-lin LI1,2, Feng GAO1,2
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. Hunan Key Laboratory of Mineral Resources Exploitation and Hazard Control for Deep Metal Mines, Changsha 410083, China
Received 14 January 2016; accepted 6 June 2016
Abstract: Undercut is one kind of important spaces to place the mining blocks in the mass underground mining. This structure is also used as a compensation space during blasting. In the process of underground mining in the fragment orebody, it is important and critical to analyze the stability and blockage of the three-dimensional wedges created around the undercut space. The wedge stability is mainly controlled by factors including geometry (i.e., the size, shape and spatial location of the wedge and undercut), the strength (shear and tensile) of the discontinuities that created the wedge, and the stress distribution within the rock mass. The Unwedge software was used to conduct the orthogonal simulation tests (three factors and five levels) that considered different cross sections, trends, and plunges of the undercut space. The results demonstrate that the control value of the safety factor of wedge is set to be 1.2. The optimal parameters are determined in the undercut space, such as the blasting fragmentation, orientation of the fluid flow, and the equipment gradeability; the wedge stability can be evaluated in the light of the block images and continuous falling; the stability of the key block meets the needs of the undercut space, the parameters gained are reasonable and optimal. Cross section is 27°, trend is from 315° to 325° (it is 320° at in-suit test) and plunge is 5°.
Key words: wedge stability; fragment orebody; undercut; Unwedge software; optimization
1 Introduction
In underground mine, developing engineering spaces is an important structure for efficient mining. As for the mining object, orebody and rock masses are both complicated earth media that contain various discontinuities. If their extent is large enough and intersect with each other, ore rock will become discrete. The discrete rock masses become one kind of spatial structural shapes, which are called blocks. The main failure mode in an underground excavation, especially for fragment orebody, is the movement of the unstable rock blocks. The prediction and prevention of such block falling demand a removability analysis of rock blocks based on a precise characterization of discontinuities within the rock masses. At present, a lot of attention has been paid to the stability of the key block of these structures as it lost its stability after first-step excavation in underground engineering [1,2]. Under the influence of gravity, stress concentration and other forces, roof and wall wedges may fail either by falling, sliding or by rotating out of their sockets. The wedge stability is generally controlled by factors including geometry (the size, shape and spatial location of the wedge and the trend), strength of the discontinuities that create the wedge, and stress distribution within the rock mass [3,4]. Two types of instability are readily observed around underground openings; one is structurally controlled gravity-driven processes leading to wedge type falls-of-ground, the other is stress-driven failure or yielding [5]. The block theory, firstly proposed by GOODMAN and SHI [6] in 1985, makes it possible to analyze the stability of rock blocks on slopes or around underground openings. The aim of block theory is to identify so-called “key blocks” or critical blocks which present particular risk to the stability of an excavation boundary. Using the theory, the combination of joint sets was tested, by which finite blocks could be formed to determine the safety factors of removable blocks, as well as the maximum boundary of a region within which such blocks could possibly occur [7].
In underground excavation, many surrounding rock failures have a close relationship with joints. Dynamic model is used to study the block stability, and the results indicate that the effects of the block interface are related to the size of the block and the capability of bulk deformation included in block and interface [8]. Based on numerical simulation results,the effects of tunnel stability are studied from different dip angles of layered joints and the lateral pressure coefficient in jointed rock mass [9]. For the Mathew method, the principal concept behind the stability graph is that the size of an excavation surface is related to the rock mass competency to give an indication of stability or instability [10]. Based on the block theory, the Unwedge program was designed. It is a 3D stability analysis and visualization program for underground excavations in rock containing intersecting structural discontinuities. Unwedge can be used to determine all of the possible wedges which are formed by the intersection of the 3 joint planes during the excavation. The influence of in-situ stress on potential wedges can be calculated with the program [11]. Safety factors are calculated for potentially unstable wedges and support requirements can be modeled using a variety of supporting form, such as spot bolting and shotcrete. Key block theory was widely used in hydro-electric engineering and the stability analyses of slopes [12]. Using the Unwedge program, the key blocks and some limitations were discussed in large underground excavation [13] to verify the “near field” and the “far from field” stability conditions of an underground room and pillar mine [14]. Speaking of the rock masses of various joint patterns [15], the stability analysis of rock wedges was also studied using the software based on block theory for each section of the cavern, and at the same time, it was used to optimize the design of the tunnel, which included the choice of hole shape, the trend of the tunnel and support parameters [16].
The undercut space is constructed backward in the tunnel. The main issue is the stability of large blocks and wedges. These wedges can form blockages in the undercut and prevent the mine discharge. Therefore, the safety factors (FS) and the volume of the wedges are necessary to be known. With the assistance of the Unwedge program, the large block analysis was investigated and the factor of safety was found through different cross-sections, trend and plunge of the undercut. Taking the effect of the blasting and the underground water on structure stability into consideration, the FS was added to the two coefficients due to the blasting effect and the underground water effect. Exposed areas of the wedges were analyzed in the undercut using 3DMine program. The relationships were obtained among the ratio of the exposed area, the volume, and the FS in the undercut wedge. According to optimized results by orthogonal experiments, the optimal parameters of undercut were analyzed in this work.
2 Description of problem
2.1 Master joints and stress field
Kalatongke copper and nickel mine is situated in the Fuyun County of the Xinjiang, China and on the northeast edge of the Junggar Basin. It is the second largest nickel deposit in China with a nickel metal production of 8000 t/year. The nickel ore contained in an ultrabasic rock mass. The main orebody zone strikes NW 25°-45° and has a dip angle of 70°-85°. Orebody thickness is varied in the range of 9.0-24.5 m. The test ore section is situated in lines 18-20. The buried height is 300 m to the test stope in the range of 651-598 m.
Kalatongke mine is a copper and nickel orebody with fragment rock masses. In general, the mineralization of copper and nickel is magma intrusion from the fault zone. In the orebody and surrounding rock mass, there are many joints, fractures and faults. According to the results of the geotechnical survey, there are three main sets of joints in the Kalatongke mine shown in Fig. 1. Three main sets of joints are found, to the dip orientation and dip, set 1 is 131°<86°, set 2 is 81°<62° and set 3 is 226°<72°.
In the mine, the results of in-suit stress showed the laws of the stress field as follows.
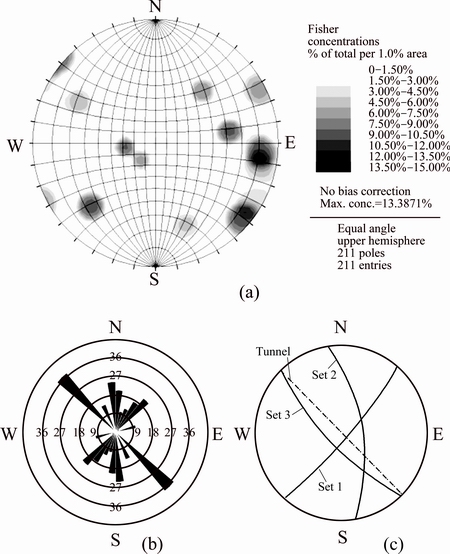
Fig. 1 Contour diagram of joints (a), rose diagrams of dip orientation (b) and stereogram of main joint sets (c)
1) Two principal stresses are nearly horizontal and the third is nearly vertical. The value of the maximal principal stress is 1.19-1.54 times of the gravity stress. The axis orientation is NW 30°.
2) Along the orientation, the middle and the minimum principal stress are inclined, but the angle is small. In the simulation, the angle is ignored.
3) The vertical stress is equal to or a little greater than the weight of the overburden. In the simulation, the value of vertical stress is equal to the weight of the overburden. The stress state is the compressive stress. We didn’t find the tensile stress in the process of the measurement. Two principal stress values are calculated by Eq. (1):
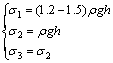 (1)
(1)
where σ1 is the maximal principal stress, and the coefficient value is 1.2 in this work; σ2 is the gravity stress which changes with the height; σ3 is the minimal principal stress, and the coefficient value is 1.
The trend of maximal principal stress is 330° in the horizontal. The buried height is up to 300 m. Thus, the values of the stress are calculated by Eq. (1). The cohesion of mechanical joint is 0.2 MPa, and the friction angle is 30°.
2.2 Mining method
Aiming at this kind of ore, it is a traditional mining method of the downward drift and back filling mining or the development downward drift and back filling mining. Due to the disadvantages like the low productive capacity, labor-intensive, and higher costs, the method was changed from the down drift mining to the strength and induction caving method. A panel stage continuous caving method was proposed in the unstable orebody compared with other nine mining methods based on the fuzzy theory [17]. The industrial field test was carried out at Kelatongke Copper-Nickel Mine [18]. In this work, the stability was analyzed in the light of the back-filling mining method using the concept of environmental reconstructed deep-hole induce-caving. The rationality of the mining method used in the fractured orebody was confirmed. The down-toward cementation and filling mining method was proposed in the Jinchuan Mine No.2 based on the fuzzy mathematics [19]. The results showed that the working security was improved greatly, the production capacity was increased highly, the overall economic benefits was improved after using the down-toward cementation and filling mining method in the Jinchuan Mine No.2. So, it is very important to select a reasonable mining method according to the mining conditions. The mining space structures were reconstructed from the roof, column and bottom structures. For the fractured orebody, it is fundamental to carry out the mass mining by the deep-hole blasting and lateral caving in the reconstructed mining environment (see Fig. 2).
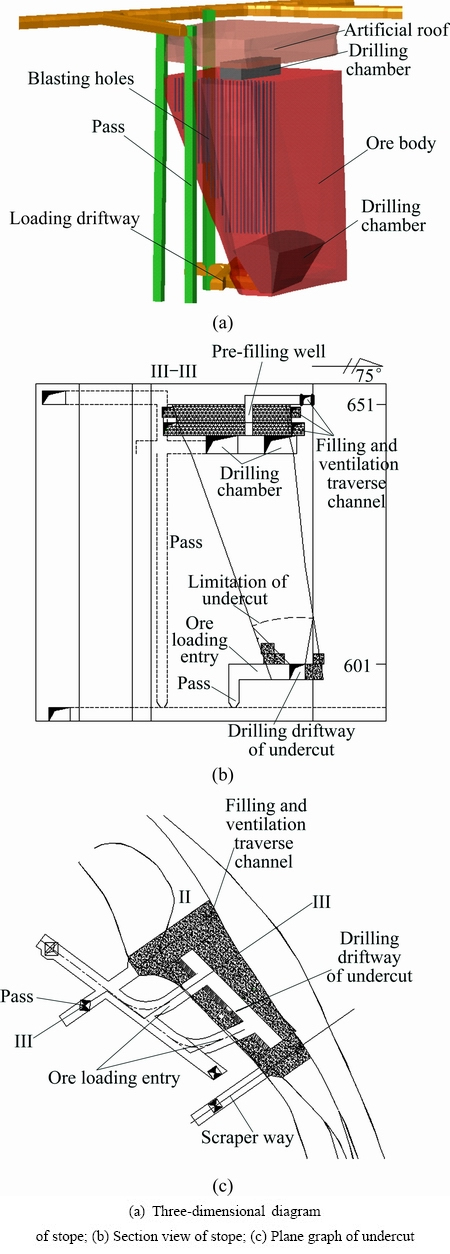
Fig. 2 Section view and plane graph of undercut in reconstructed mining method
The basic thoughts are as follows: Firstly, the roof and column are reconstructed in the fractured ore-body by the drift mining method and back filled by concrete. Secondly, the bottom structure is built in the same way. The aim of the first two steps is to protect the safety of the mining and ore loading space, and work environment. In order to keep the safety of the discharge space, the concrete backfill is used to reconstruct the boundary of the undercut and the ore removal system structure. The stability of the wedges should be guaranteed for the undercut space. Thirdly, the undercut space is formed by means of drilling blasting. In the reconstructed mining environment, the bottom structure is used for the undercut space and compensation space of mining.
2.3 Influential factors and optimal principle
In the underground mine, the influential factors include the geological conditions of joints, engineering features, joint properties and stress conditions. In the undercut space, there are three aspects of the stability factors including geometry of the wedge and undercut, stress field and joint properties (see Fig. 3). In general, joint properties and the field stress value are assumed to change in a limited and small range for the same mine.
As we know, the geological conditions of joints include the joint set parameters, the spatial location, and the wedge shape. Two parameters of the joint set, the dip and dip direction, control the joint distribution, which influences the wedges shape and the volume through the intersect cut in the rock mass or orebody. The spatial locations of joints influence the wedge location in the underground space. In the undercut, the spatial location is not important to enhance the stability by the shotcrete- bolt support technology. But the volume of the wedge is important to the function running of undercut.
If the scale of the wedge volume is large, blockages will form in the undercut space, and the discharge would be stopped to handle the large scale wedge by the second blasting. It is called the key block in the undercut. If the block volume is large enough to form the blockage in the undercut, after ore falls down, it is difficult to carry out a second blasting in the block, by which to make sure to discharge in the mining process smoothly, as seen in Fig. 4. When the large scale blocks fall down, there are two kinds of damages in the undercut. On the one hand, the reconstructed bottom is damaged by the force of falling down, and at the same time the block will slide in the undercut wall. On the other hand, the passages are blocked by the large scale blocks in the undercut space. When the undercut is formed, we handle the small size block firstly, which is less than 300 mm.
The engineering feature is the geometry of the undercut. It is the optimal parameters in the case study. The wedges were formed from the 3 sets joints and the excavation face. These factors are important to the safety of engineering. In this work, the results were analyzed by Unwedge program. In this program, the safety factor of wedge (FS) was defined as follows:
 (2)
(2)
where FS is safety factor of the wedge without supporting; 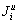 is resisting force arising from shear strength of joint i; Ti is resisting force arising from the tensile strength of joint i; A is resultant active force vector;
is resisting force arising from shear strength of joint i; Ti is resisting force arising from the tensile strength of joint i; A is resultant active force vector;  is sliding direction; τi is shear strength of the ith joint; ai is area of the ith joint; θi is angle between the sliding direction and the ith joint; σti is tensile strength of the ith joint; W is wedge weight vector; C is shotcrete weight and X are resultant active pressure force vector; C and X are zero due to without any support; U is water force vector and E is seismic force vector. In this case, U and E are taken into account for the coefficients of the influential efficiency of underground water (fwater) and the influential efficiency of the blasting (fblast); γr is the density of rock; V is the volume of the block;
is sliding direction; τi is shear strength of the ith joint; ai is area of the ith joint; θi is angle between the sliding direction and the ith joint; σti is tensile strength of the ith joint; W is wedge weight vector; C is shotcrete weight and X are resultant active pressure force vector; C and X are zero due to without any support; U is water force vector and E is seismic force vector. In this case, U and E are taken into account for the coefficients of the influential efficiency of underground water (fwater) and the influential efficiency of the blasting (fblast); γr is the density of rock; V is the volume of the block;  is the acceleration of gravity.
is the acceleration of gravity.
The stress field and the joint properties showed the essential feature of the underground mine. It is important for the stability of the wedges.
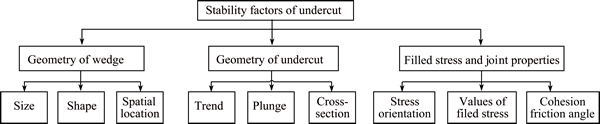
Fig. 3 Graph of stability factors in undercut space

Fig. 4 Key block and blockage between key block and undercut space
2.4 Principles of optimal parameters
For safety excavation, the safety factor in underground mining should be within 1.1-1.3. Actually, undercut is an important space to ensure the safety of discharge and mining process. Considering the disturbances of blasting effect and the strength decrease for the underground water, the safety efficiencies must be added in the FS. One is the blasting efficiency, and the other is the water efficiency. So, the FS would exceed 1.872, as seen in Eqs. (2) and (3).
FS=(1.1-1.3)fwaterfblast (3)
where the base factor safety is 1.1-1.3, in general, the value is assigned to be 1.2; fwater is the influential efficiency of the underground water, and its value is 1.3; fblast is the influential efficiency of the blasting, and its value is 1.2. According to the importance of the trend, FS is up to 1.872.
1) The plunge accords with the plunge of the drilling driftway in undercut (see Fig. 2). In the drilling driftway in undercut, the plunge was designed to be 5°. In this part, the first task is to plunge orientation. It is an advantage to water gravity flow, and no load is uphill and heavy load is downhill. Secondly, the angle is more than 3° to meet the water gravity flow and less than 10° to satisfy the gradeability of underground scraper.
2) The trend accords with the trend of orebody in the undercut. Pointing at the function of the undercut, the main purposes are gathering the mine block and providing a passage for underground scraper to carry ore. The trend is limited in the range of the orebody boundary and in accordance with the trend of the orebody. According to the trend of the bottom and top boundary in the orebody, the trend range is from 315° to 335° (see Fig. 2).
3) As for the cross section of the undercut, the main parameter is R or the radian of the arc in the roof (θ), as seen in Fig. 5. It must satisfy the following needs. On one hand, the design of the roof arc should be convenient for drilling blasting in the underground mine. Small radians of roof arc are beneficial to blast design and mass caving. On the other hand, this form of cross section is advantageous to form the blast block of medium size. The height of the arc is not high. The blind zone of blasting can be avoided in the deep hole. At the same time, the key wedge stability must meet FS>1.872.
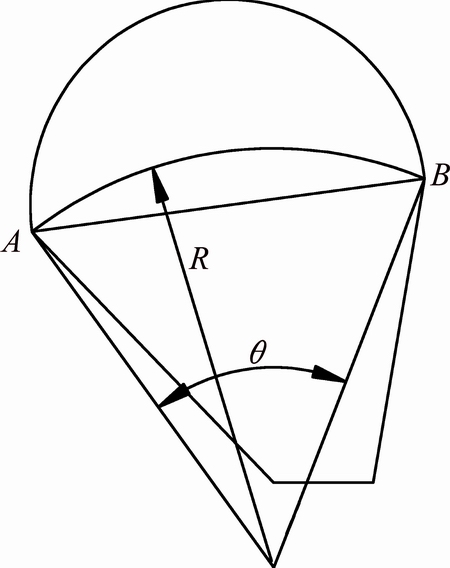
Fig. 5 Graph of undercut cross section
3 Methodology
With the cases of different cross-sections, trends, and plunges of the undercut space, the orthogonal simulation tests were carried out by means of Unwedge program.
In the simulation, the influence factors were evaluated and limited to meet the demands of undercut using the orthogonal experiments. In the light of the condition of the undercut, the level of the influential factors was designed from 2 to 10, as seen in Table 1.
Table 1 Influential factors and levels in numerical simulation
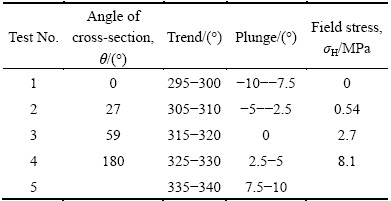
In this model, the feature value was defined as θ, ranging from 0°, 27°, 59° to 180°. The trend of the undercut varies from 295° to 340° with an interval of 5°. For the plunge, it is similar to the tunnel of undercut. The plunge is between 0 and 10 with an interval of 2.5°. Under the plunge, smooth water gravity flow and free running of the scraper can be ensured. As for other influential factors, the field stress was taken into account for the stability of the wedge.
4 Results
4.1 Optimal parameters
Simulation results demonstrated a complicated relationship between the trend (cross-section, plunge and field stress) and FS. In general, FS increases with the increase of trend and plunge, and decreases with the decrease of θ. In terms of the field stress, the FS varies a lot under different field stresses.
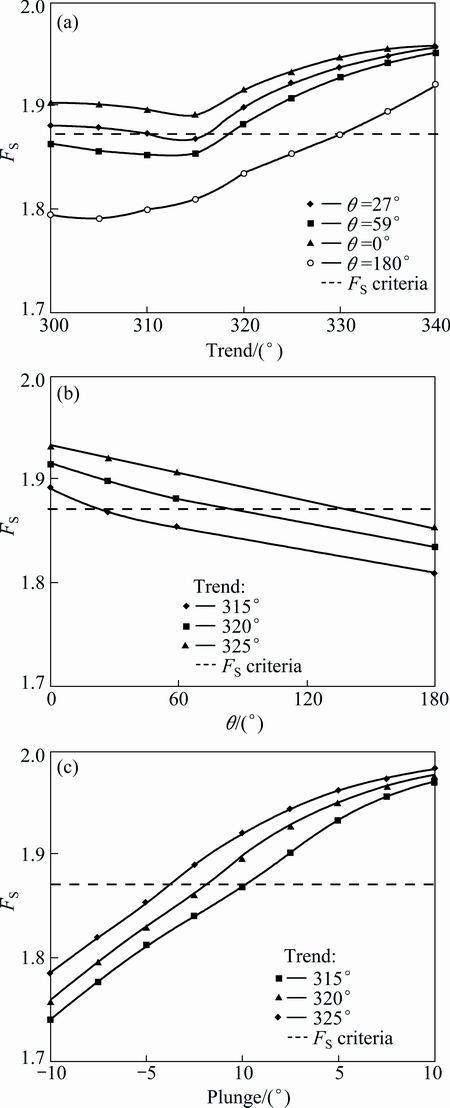
Fig. 6 Relationship between FS and trend (a), θ (b) and plunge (c)
From Fig. 6(a), we can find that there is an approximately positive relationship between the FS and the trend when passing the inflection points. In general, the value of FS increases as the trend of undercut increases. There is an inflection point at the trend value of 315° to the growth rate. So, the optimal trend should be larger than 315°. Meanwhile, the FS should be larger than 1.873 to guarantee the maximum accepted mine volume because of the limitation of orebody trend, which is the main orebody zone strikes NW 25°-45°. The optimal trend is 320°.
Figure 6(b) shows that FS varies approximately linearly with different cross-section, and it reduces as θ increases. In the light of FS>1.872 and the radius of the roof, θ is selected from 0° to 59° in the undercut cross section.
The advice is to set θ° to be 15°-45°, which is advantageous to the blasting design and the control of the blasting block size. The design has advantages including that the FS is large to meet with the stability, and it is advantageous to control the size of the blasting blocks. In the end, the selected θ is 27° to the optimal roof angle.
Two key factors influence the design of the undercut plunge. The first factor is plunge that influences underground water flow naturally along the tunnel plunge. The second factor is the plunge that is greater than 10°, the angle of which influences the gradeability of the equipment. From Fig. 6(c), FS increases approximately linearly as plunge increases, and the value of the FS tends to be a constant value just below 2. When the trends are 315°, 320° and 325°, respectively, the FS is more than 1.872 under the plunges more than 2.5°, which meets the requirements. Due to the angle of water gravity flow and the gradeability of equipment, the optimal plunge was selected as 5°.
In the end, the optimal parameters of the undercut were determined. Cross section was 27°, which means that the radius of the roof is 26.3 m. The trend of the undercut from the X-coordinate was 315°. It is coincided with the trend of the bottom orebody. It is advantageous to gather mine block in the process of blast mining. The angle of undercut plunge was determined to be 5°. It meets the demands of the factor of safety, the angle of gravity water flow and the gradeability of the equipment.
4.2 Stability factors
In the underground, the ground stress is the main influential factor for the stability of the underground engineering. As seen in Fig. 7, simulation results show that it is a positive correlation between ground stress and FS. When the stress is ignored in the simulation, the value of FS is very small. It varies from 0.19 to 0.21. The wedge is extremely unstable. However, stress field does not exist. FS is then found to vary from 1.44 to 1.98. That is to say, the state changes from the instability to stability. This phenomenon probably can be attributed to parameter 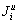 arising from the ground stress. When the depth increases to larger than 100 m, the value of ground stress thus goes up to 2.7 MPa. Underground engineering structures are stable as FS is 1.872.
arising from the ground stress. When the depth increases to larger than 100 m, the value of ground stress thus goes up to 2.7 MPa. Underground engineering structures are stable as FS is 1.872.
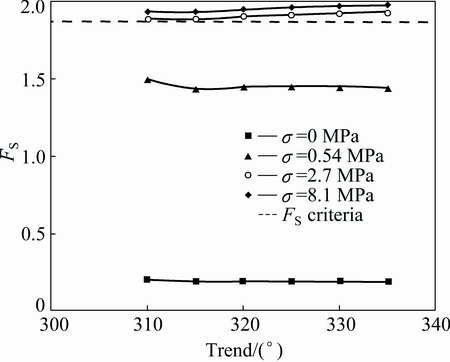
Fig. 7 Relationship between FS and gravity stress
In order to investigate the effect of the block size, two parameters were taken into account, the ratio value ζ and wedge volume V. The ratio value ζ is defined as the ratio of the exposed area of the wedge to the wedge volume.
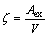 (4)
(4)
On the other hand, the wedge volume is a key point for the stability in the undercut roof. From Fig. 8(a), the volume increases as the trend increases. At the same time, the FS increases as the trend increases. From the change rate of the volume, there is a turning point from the second point and the trend angle is 315°. As for the value of FS, the slope changes from small to large. The variation of FS is related to the exposed area in the undercut. In the mining, the laws were obtained in the relationship between the stability and the exposed areas. Such as the Mathew method, the principal concept behind the stability graph is that the size of an excavation surface can be related to the self-supporting capability of rock mass, which can give an indication of stability or instability. On the whole, the stability is negatively associated with the exposed area. With increasing the exposed area, the stability becomes worse in the underground space. As a wedge, the stability is related with the volume and the exposed area. According to the results gained by Unwedge, 3DMine program was used to calculate the wedge exposed area when θ=27° or 59° and the plunge is 5°, as seen in Fig. 8(b). There is a negative relationship between ξ and FS. This can probably give an explanation for the increment of wedge stability.
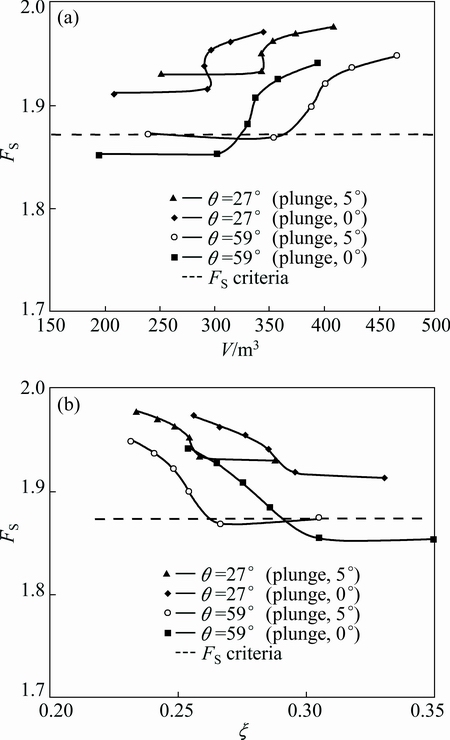
Fig. 8 Relationship between FS and V (a) and ξ (b) in undercut
4.3 In-suit verification of proposed model
In-situ test was conducted to verify the optimal parameters proposed in this paper. From the results of the undercut stability and the blasting mining, key blocks are stable in the undercut space. The size of the blocks is medium (<300 mm), which meets the demands of blasting block. In general, the largest scale is less than 300 mm, as seen in Fig. 9. The mine discharging is continuous in the undercut, and the blockage is not able to be found.
In-suit test has advantages to produce the better size distribution of rock blocks from the statistical visible effect. The view showed that the large scale volume of wedges was stable in the roof of undercut. It did not fall down to block the undercut. The optimal parameters were stratified with stability and mining.
5 Conclusions
1) The safety factor FS is important for the stability of the undercut space. Taking the mining blasting distribution and the strength parameter’s decrease by the underground water into consideration, two efficiencies are added to the FS formulation, which are the blasting and water efficiencies, the values are 1.2 and 1.3, respectively. In the end, FS is identified to be 1.872.

Fig. 9 Rock blocks after blasting
2) In the undercut space, the FS can be adjusted according to the cross section, trend and plunge of the undercut. Optimal parameters are produced in virtue of simulation tests. Cross section is 27°; trend is from 315° to 325° (it is 320° at in-suit test) and plunge is 5°.
3) In the underground mine, the field stress must be taken into account during key block analysis. In this case study, the FS varies from 0.19 to 1.98 under different stress fields. The industrial experiment shows that there is no large scale block to block the space during mine discharging, and the undercut is stable.
References
[1] CHEN Yi-feng, ZHENG Hua-kang, WANG Min, HONG Jia-min, ZHOU Chuang-bing. Excavation-induced relaxation effects and hydraulic conductivity variations in the surrounding rocks of a large-scale underground powerhouse cavern system [J]. Tunnelling and Underground Space Technology, 2015, 49: 253-267.
[2] LIU Jun, LI Zhong-kui, ZHANG Zhuo-yuan. Stability analysis of block in the surrounding rock mass of a large underground excavation [J]. Tunnelling and underground space technology, 2004, 19(1): 35-44.
[3] CURRAN J H, CORKUM B, HAMMAH R E. Three-dimensional analysis of underground wedges under the influence of stresses [C]//Proceedings of the 6th North American Rook Mechanics Symposium (NARMS). Houston: American Rock Mechanics Association, 2004.
[4] YANG Xu-xu, KULATILAKE P H S W, JING Hong-wen, YANG Sheng-qi. Numerical simulation of a jointed rock block mechanical behavior adjacent to an underground excavation and comparison with physical model test results [J]. Tunnelling and Underground Space Technology, 2015, 50: 129-142.
[5] MARTIN C D, KAISER P K, CHRISTIANSSON R. Stress, instability and design of underground excavations [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(7): 1027-1047.
[6] GOODMAN R E, SHI G. Block theory and its application to rock engineering [M]. Englewood Cliffs, NJ: Prentice-Hall, 1985.
[7] SONG J J, LEE C I, STEO M. Stability analysis of rock blocks around a tunnel using a statistical joint modeling technique [J]. Tunnelling and Underground Space Technology, 2001, 16(4): 341-351.
[8] WANG Ming-yang, QI Cheng-zhi, QIAN Qi-hu. Study on deformation and motion characteristics of blocks in deep rock mass [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2825-2830. (in Chinese)
[9] MA K, TANG C A, WANG L X, TANG D H, ZHUANG D Y, ZHANG Q B, ZHAO J. Stability analysis of underground oil storage caverns by an integrated numerical and microseismic monitoring approach [J]. Tunnelling and Underground Space Technology, 2016, 54: 81-91.
[10] MAWDESLEY C, TRUEMAN R, WHITEN W J. Extending the Mathews stability graph for open-stope design [J]. Mining Technology, 2001, 110(1): 27-39.
[11] HOEK E. Practical rock engineering [EB/OL]. [2007-05-28]. http://www.rockscience.com/education/hoeks_corner.
[12] SUN Jun, WANG Si-jing. Rock mechanics and rock engineering in China: Developments and current state-of-the-art [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(3): 447-465.
[13] XIE Ye, LIU Jun, LI Zhong-kui, ZHANG Zhuo-yuan. Stability analysis of block in surrounding rock mass of large underground excavation [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(2): 306-311. (in Chinese)
[14] PEILA D, PELIZZA S, GUARDINI C. Underground exploitation of a granite mine by large voids: Stability aspects [J]. Human Pathology, 2007, 45(2): 316-319.
[15] MANDAL A, CHAKRAVARTHY C P, NANDA A, RATH R, USMANI A. Analysis and design approach for large storage caverns [J]. International Journal of Geomechanics, 2011, 13(1): 69-75.
[16] SHAO Guan-hui, LI Xiao-zhao, ZHAO Xiao-bao, JI Cheng-liang, WANG Yi-zhuang, YUAN Liang. Tunnel design optimization based on safety factor of key-block theory [J]. Journal of Engineering Geology, 2010, 18(4): 581-585. (in Chinese)
[17] YE Hai-wang, FANG Liu. Underground mining method selecting system based on fuzzy theory [J]. Advanced Materials Research, 2011, 402: 631-635.
[18] ZHOU Ke-ping, LIU Ze-zhou, XIAO Xiong, WANG Li-li. Numerical analysis of stope stability based on coupling of MIDAS/GTS and FLAC 3D [C]//Proceedings of the 2nd International Conference on Computer Engineering and Technology (ICCET). New York: IEEE, 2010: 182-186.
[19] ZHANG Hong-jun, ZHANG Xiao-yi. Application of fuzzy mathematics in optimal selection of mining method in Jinchuan Mine No. 2 [C]//Proceedings of the Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD). New York: IEEE, 2011: 603-606.
胡建华1,2,杨 春1,2,周科平1,2,李杰林1,2,高 峰1,2
1. 中南大学 资源与安全工程学院,长沙 410083;
2. 湖南省深部金属矿开发与灾害控制重点实验室,长沙 410083
摘 要:底部结构是地下矿山规模开采的重要工程结构和爆破补偿空间。在碎裂矿段的地下采矿过程中,对底部空间的块体结构和三维岩石楔体开展稳定性分析是采矿成功的关键。楔体的稳定性主要由地质因素(包括底部结 构与楔体的工程尺寸、形状和空间位置)、产生楔体结构的不连续面的剪切强度和抗拉强度以及岩体应力分布控制。应用Unwedge软件,设计横断面夹角、底部结构走向和倾角3因素、5水平的正交试验,获得底部结构的优化设计参数。研究结果表明:地下空间的安全系数为1.2,底部结构的参数优化由爆破块度、水流方向和设备爬坡能力决定;楔体的稳定性根据块体形状和连续冒落进行分析;优化参数为断面夹角27°、走向315°~325°、倾角5°,满足底部结构空间块体安全稳定性要求,是合理优化的设计参数。
关键词:楔体稳定性;碎裂矿段;底部结构;Unwedge软件;优化
(Edited by Wei-ping CHEN)
Foundation item: Project (2015CX005) supported by Innovation Driven Plan of Central South University, China; Project (2016zzts451) supported by the Graduate Innovation Fund of Central South University, China; Project (2016JJ21) supported by the Fundamental Research Funds for the Hunan Province, China; Project (2012BAB14B01) supported by the National Science and Technology Pillar Program during the 12th Five-year Plan Period of China
Corresponding author: Jian-hua HU; Tel: +86-13787056402; E-mail: hujh21@126.com
DOI: 10.1016/S1003-6326(16)64305-4

