­­ Non-local damage and fracture model of rock and concrete-like materials

BI Zhong-wei(毕忠伟)^{1, 2}, ZHANG Ming(张 明)¹, JIN Feng(金 峰)¹

1. State Key Laboratory of Hydroscience and Hydraulic Engineering, Tsinghua University, Beijing 100084, China;

2. School of Urban Construction, University of South China, Hengyang 421001, China

Received 10 August 2009; accepted 15 September 2009

Abstract: In view of the non-local phenomena appearing in the rock and concrete-like materials, the non-local damage and fracture model of rock and concrete-like materials was established through non-local method of Gaussian weighting function. The result indicates that, the stress of one point in the material is correlated not only to its strain history, but also to the interaction of the points in its certain adjacent region of the material. Based on the established non-local model, the numerical simulation of notch containing three-point bending beam was carried out. The results show that the grid sensitivities have been avoided and the fracture direction of the material has not been influenced by the grid shape, and the model proposed can be used to better simulate the damage developing process of the rock and concrete-like materials.

Key words: non-localization; rock and concrete-like materials; damage model

1 Introduction

In the test and engineering process of rock and concrete-like materials, it has been found that when the bearing capacity achieves the peak value, the material distortion concentrates in a narrow belt-shaped region and the strain localization phenomenon occurs. Furthermore, there appears a very high strain gradient in the local region; and its stress and strain present a high-order nonlinear change[1]. The traditional elastoplasticity theory only maps the load―displacement relation as stress―strain relation, but does not consider the microstructure change and interaction of the material interior. Simultaneously, there is a lack of internal characteristic scales to reflect the microscopic characteristics of the material in the traditional elastoplasticity theory. So, the traditional elastoplasticity theory cannot explain strain localization phenomenon [2]. The non-local theory is exactly based on the above two considerations, namely, introducing the material interior characteristic scales in the traditional constitutive model to carry non-local processing to the local variable, and indirectly considering the microstructure change and interaction of the material interior[3-5].

The non-local theory was established by ERINGEN[6], KRONER and DATTA[7], EDELEN[8], KUNIN[9]. BAZANT and LIN[10] proposed the non-local model of quasi-brittle materials based on the dissemination fault zone method and the softening plastic theory, and applied it to the stability analysis of non-lining tunnel excavation. BAZANT and OZBOLT [11] developed one kind of non-local micro-plane model by simulating the crack behavior of quasi-brittle materials. This model is applied to analyzing the size effect of crack behavior in concrete structure.  JIRASEK and ZIMMERMANM[12] proposed and developed the non-local rotating crack-scalar damage mechanics model. PIJAUDIER and BENALLAL[13] studied the localization properties under critical conditions when the bifurcation possibly occurs in the simulation of localization by non-local damage model and the wavelength distribution of the strain localization belts. YAO and HUANG[14], ZHAO et al[15], WANG and MENG[16], HUANG et al[17] researched the non-local theory.

In the present work, Gaussian weighting function was taken as the non-local method, by using damage power consumption rate to express the damage factor. The non-local damage model of the rock and concrete-like materials was proposed, and the damage evolutionary process of this kind of materials through numerical simulation of notch with three-point bending beam was studied.

2 Non-local damage model

2.1 Weighting function

According to the non-local theory, the stress situation of one point not only is correlated to its strain condition, but also is decided by its adjacent strain field. Namely, when one point of the material has the destruction or the strain softening, the strain softening will extend to its adjacent region from this point, and the extended scope will be decided by the heterogeneous degree of the material, which is usually expressed by the characteristic scales of the non-isotropic materials. In order to consider the non-local damage or strain softening in the material constitutive model, the non-local method is adopted in processing the field quantity, namely, using the weighting mean value of the adjacent field quantity of some points in the solving domain to replace the local field quantity in the original spatial point. Taking some local variable f(x) to solve domain V as an example, the corresponding non-local variable can be defined as

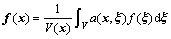                 (1)

where α(x, ξ) is the non-local weighting function. In the infinite domain, the weighting function only relies on the distance between the source point ξ and the target point  x. But at the boundary site, it is approaching the solving domain. And α(x, ξ) needs to be carried out on scale conversion. Thus, the integral operation in Eq.(1) will not change the local variable which has been defined originally as an uniform distribution.

One simple definition is as follows:

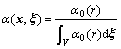                         (2)

where α₀(r) is the monotone decreasing nonnegative function of the distance, and 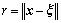. This definition has changed the symmetry of ξ and x in the weighting function. For this reason, POLIZZOTTO[13] and BORINO et al[4] proposed another kind of weighting function:

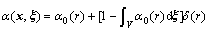           (3)

Although the selection of weighting function is very important to calculation result, there is still no accurate method to reasonably determine the expression form of the non-local weighting function. Through the comparison of different forms of weighting functions, the results got by Gaussian weighting function are better than those by others[15]. Therefore, Gaussian weighting function is selected:

                         (4)

where n_dim is the constant correlated to the spatial dimensions in the solving domain; l is the internal characteristic scale of the non-local model, which has showed the size of the non-local effect. When l is large, the non-local effect of the material is obvious; otherwise, the effect is not obvious.

2.2 Non-local damage model

The non-local damage model is based on the continuous medium damage mechanics model to replace the localization variable parameter by the local variable of the weighted average integral in the affected adjacent region. By damage mechanics, the stress―strain relationship under the localization condition is:

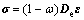                              (5)

where σ and ε are the stress and the strain, respectively; ω is the damage factor; D_e is linear elastic stiffness matrix.

Eq.(5) indicates that the damage factor is equal to the stiffness-reducing factor. When the damage increases, the linear elastic stiffness matrix reduces. According to Bazant’ suggestion, the damage factor can be expressed

as the damage power consumption rate, ,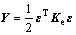

which is taken as the non-local variable. The size of the damage factor will be determined by the maximum value (Y_max) of non-local damage power consumption rate in the loading process, and the damage evolution can be displayed as

ω=f(Y_max)                                   (6)

Suppose Y₀ is the threshold of the critical damage in the non-local model by Eq.(6). When Y＜Y₀ for each point in the material, Y_max is also lower; when ω=0 for the damage factor of each point, the material is in the elastic stage, which has guaranteed that the damage factor is equal to the localization model in the elastic stage.

In order to get the value of the various variables in the above formulas by the finite element method, the discretization must be carried out. According to the principle of virtual work, the stress in some regions can be transformed to the sum total of the Gaussian stress distribution in the grid to the internal force vector contribution. Supposing B(x) is the strain―displacement geometry transfer matrix, then the discrete form of the internal force vector f in the solving domain is

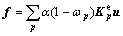                         (7)

where α is integral weighting factor; 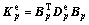 is

the elastic stiffness matrix; p is the total number from 1 to Gaussian point of the solving object. Similarly, the damage power consumption rate in the integral range can also be discreted as:

                             (8)

where β is the mutual influence coefficient of each point in the material interior, which is determined by the integral weighting function and the integral range.

When the numerical calculation is carried out according to the above-mentioned non-local damage model based on the finite element method, the increased iterative calculating method is usually adopted. By Eq.(6), the damage coefficient of each point in the material interior is correlated to the strain history, but the changing process of the stress (ε) of one point is determined by the distribution of the system displacement u. Therefore, the partial derivation of the damage coefficient of any Gaussian point to the displacement vector can be obtained firstly. Supposing the damage power consumption rate is Y_p in the Gaussian point x_p, then the corresponding partial derivative is

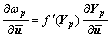                           (9)

The local power consumption rate in the Gaussian point x_p is:

                             (10)

Substituting (10) to Eq.(9) yields

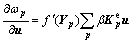                      (11)

Carrying the derivation of displacement in both sides of Eq.(7), the stress―strain relationship of non-local damage model is

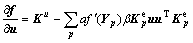             (12)

In Eq.(12), 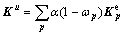is the invariant of non-damage or damage in linearly elastic stage.

Through the above derivations, the calculation method of the non-local damage model is similar to that of the local model. However, the former considers the interaction of each point in the characteristic scales of the material, which results in the fact that the overall stiffness matrix is composed of two parts, non-damage part and damage part, and that the band width of the overall stiffness matrix is increased.

3 Example

Based on the above-established non-local damage model, the numerical simulation was carried out to the fracture process of notch containing three-point bending beam by compiling corresponding computational procedures. The calculation model is shown in Fig.1, supposing the notch height is 82 mm.

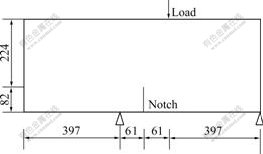
Fig.1 Calculation model (unit: mm)

Taking the displacement control method to carry out simulation, damage developing process is shown in Fig.2. The damage microcrack zone first occurs in the upper right of the notch, the upper loading point and lower pivot point. Along with the crack expansion of the notch, the bending deformation and crack occur along with the curve way, and finally stop at the loading point, which indicates that during the crack developing process, the crack expansion direction has continuous deflection along with the change of the main stress, and the simulation results much conform with reality.

Fig.2 Developing process of damage: (a) Initial damage; (b) Final damage

The final displacement vector of the material is shown in Fig.3. Along with the notch enlargement caused by the crack expansion, the vertical relative slippage also occurs, but the vertical slippage is smaller compared with horizontal splaying amount, which indicates that in the initial crack stage, the crack of three-point bending beam belongs to mixed cracking of both typeⅠand type Ⅱ; the shearing stress of the crack surface weakens after cracking, and the stress in the notch tip expands under typeⅠstress condition as main direction, finally, the material is damaged by typeⅠcrack.

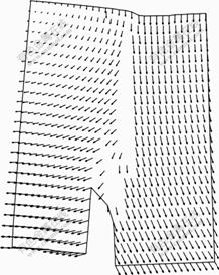
Fig.3 Displacement vector

The traditional continuous medium model does not consider the internal characteristic scales of the material. Therefore, in the localization solving, the calculation result is affected by the grid density or tendency at different degrees. Through introducing the material interior characteristic scales by the power consumption rate, evenly dividing the stress of one point in its adjacent region, the dependence of the crack to the grid  has been successfully avoided. From Figs.4 and 5, the crack expansion directions caused by the coarse and fine grids are almost the same, which indicates that the essence of the crack expansion is the dissipation of the non-linear deformation to the power, and the grid sensitivities have been successfully avoided by the method adopted by this work.

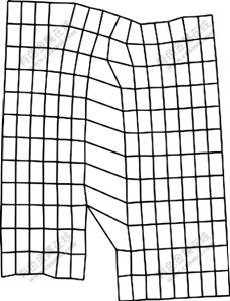
Fig.4 Coarse grid(200 times)

Fig.5 Fine grid(200 times)

4 Conclusions

1) Through damage power consumption rate, the non-local calculation method of rock and concrete-like materials is inferred.

2) Numerical simulation is conducted to notch bending beam by the model established in this work. The crack developing approach indicates that this model is in accordance with the actual situation.

3) Different grid division has little influence on cracks, which indicates that the introduction of damage power consumption rate can avoid the dependence of dehiscence on the grid, and the calculation process has nothing to do with the grid division.

References

[1] ZHANG Chu-han, JIN Feng. Discretecontact-fracture analysis of rock and concrete [M]. Beijing: Tsinghua Press, 2008. (in Chinese)

[2] BAZANT Z P, PIJAUDIER, CALT G. Nonlocal continuum damage: Localization instability and convergence [J]. Journal of Appl Mech, 1988, 55: 287-293.

[3] POLIZZOTTO C. Remark on some aspects of nonlocal theories in solid mechanics [C]// Proc of 6th National Congr. SIMAL. Chia Laguna, Italy: CD-ROM, 2002.

[4] BORINO G, FAILLA B, PARRINELLO F. A symmetric formulation for nonlocal damage models [C]// MANG H A, RAMMERSTORFER F G, EBERHARDSTEINER J. Proc of 5th World Congress on Computational Mechanics(WCCM V). Vienna, Austria: Vienna Univ of Technology, 2002.

[5] NOWINSKI J L. On the non-local aspects of stress in a viscoelastic medium [J]. International Journal of Nonlinear Mechanics, 1986, 21(6): 439-446.

[6] ERINGEN A C. A unified theory of thermomechanical materials [J]. International Journal of Engineering Science, 1966, 4(2): 179-202.

[7] KRONER E, DATTA B K. Nichtlokale elastostatik: Ableitung aus der Gittertheorie [J]. Z Phys, 1966, 196: 203-211. (in Russian)

[8] EDELEN D G B. Protoelastic bodies with large deformation [J]. Archive for Rational Mechanics and Analysis, 1969, 34: 283-300.

[9] KUNIN I A. Theory of elasticity with spatial dispersion [J]. Prikl Mat Mekh, 1966, 30: 866-877. (in Russian)

[10] BAZANT Z P, LIN F B. Nonlocal smeared cracking model for concrete fracture [J]. Journal of Stractural Engineering, 1988, 114: 2493-2510.

[11] BAZANT Z P, OZBOLT J. Nonlocal microplane model for fracture, damage and size effect in structures [J]. Journal of Engineering Mechanics, ASCE, 1990, 116(11): 2485-2505.

[12] JIRASEK M, ZIMMERMANM T. Rotating crack model with transition to scalar damage [J]. Journal of Engineering Mechanics, ASCE, 1998, 124(3): 277-284.

[13] PIJAUDIER C G, BENALLAL A. Strain localization and bifurcation in a nonlocal continuum [J]. International Journal of Solids and Structures, 1993, 30(13): 1761-1775.

[14] YAO Yin, HUANG Zai-xing. Nonlocal model and simulation of strain localization in elastic damage problems [J]. Journal of Mechanical Strength, 2008, 30(5): 773-778. (in Chinese)

[15] ZHAO Xue-chuan,　LEI Yong-jun,　ZHOU Jian-ping. Strain analysis of nonlocal viscoelastic kelvin bar in tension [J]. Applied Mathematics and Mechanic, 2008, 29(1): 62-68. (in Chinese)

[16] WANG Xiao-ping, MENG Guo-tao. Nonlocal elastoplastic theory and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 2964-2967. (in Chinese)

[17] HUANG Mao-song, JIA Cang-qin, QIAN Jian-gu. Strain localization problems in geomaterials using finite elements [J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 465-471. (in Chinese)

(Edited by YANG Hua)

Foundation item: Project(50904036) supported by the National Natural Science Foundation of China; Project (20090450421) supported China Postdoctoral Science Foundation

Corresponding author: BI Zhong-wei; Tel: +86-10-62789237; E-mail: bizhongwei1976@163.com