J. Cent. South Univ. (2013) 20: 293–300

DOI: 10.1007/s11771-013-1487-x

Glass formation for iron-based alloys by combining kinetic and thermodynamic parameters

J. H. Willy, WANG Gang(王刚), LIU Zhong-wu(刘仲武)

School of Materials Science and Engineering, South China University of Technology, Guangzhou 510640, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2013

Abstract: The glass formation was intensively studied for Fe-based alloys. Parameters defining kinetics and thermodynamic behavior of crystallization were calculated using calorimetric measurements and physical properties of constituent elements. It is found that the critical cooling rate R_c estimated by combining kinetic and thermodynamic parameters highly correlates with measured R_c found in literatures with correlation coefficient R²=0.944, and alloy compositions with high melting enthalpy △H_m can easily form glass even without high undercooling and high value of the β-parameter of Turnbull’s theory, revealing that the glass formation in this group of alloys is mostly controlled by growth limitation. This combination of kinetic and thermodynamic parameters can be used to determine alloy composition with good glass forming ability in Fe-based alloys just using physical properties of alloying elements and calorimetric measurements.

Key words: metallic glass; glass-forming ability; iron-based alloys; critical cooling rate

1 Introduction

Glass formation in Fe-based alloys has been intensively studied during last decade due to the interesting properties found in totally or partially amorphous structures of these alloys [1–7]. Fe is the basic element to which other elements are added accordingly to improve different properties such as the corrosion resistance, mechanical properties, and magnetic properties. When designing alloy composition, it is more difficult to keep those properties and enhance glass forming ability (GFA) at the same time for this category of alloys with relatively low GFA compared with some known good glass forming alloy systems like Zr- or Pd-based systems. To overcome this difficulty, it is crucial to understand well the parameters involved in glass formation for these alloys. From a kinetic point of view, crystallization can be regarded as governed by nucleation and growth rates when a melt cools down from melting point T_m to glass transition temperature T_g. Turnbull [8] showed that both nucleation and growth rates increase with the inverse shear viscosity 1/η and he used α and β parameters with their product αβ^1/3 to study the undercooling needed for a given melt to bypass crystallization. The parameter α, related to the nucleation process, and the parameter β, which is related to both nucleation and growth processes, are functions of the melting enthalpy. From a thermodynamic point of view, GFA has been investigated through the driving force for crystallization △G^L–S which is the difference in Gibb free energy between liquid melt and crystalline phase [9–11].

Takeuchi and Inoue [12] used the regular solution model to investigate the GFA in multi- component alloys and recently proposed a sub-regular solution model fitting the Miedema’s model to calculate the mixing enthalpy △H of multi-component alloys [13]. For the GFA evaluation, the maximum fully amorphous obtainable diameter Z_max is regarded as a direct way for bulk metallic glasses (BMGs), but it is hard to measure for poor glass forming alloys. Considering that Z_max also depends on factors other than the GFA of the alloy, researchers have proposed R_c to be used as a GFA criterion [14–16]. However, it is too laborious to measure accurately R_c. Therefore, some simple criteria have been proposed by various researchers based on characteristic temperatures (glass transition temperature T_g, crystallization temperature T_x and melting temperature T_m), such as γ_m=(2T_x–T_g)/T_m by Du et al [17], γ_C=(3T_x–2T_g)/T_m by Guo and Liu [18], θ=[(T_x+T_g)/T_m]×[(T_x–T_g)/T_m]^0.0728 by Zhang and Chou [19], β=T_xT_g/(T_l–T_x)² by Yuan et al [20], ω₂=T_g/(2T_x–T_g)–T_g/T_l by Zhang et al [21], and ω=T_g/T_x–2T_g/(T_g+T_m) by Long et al [22]. The Fe-based alloy system is generally associated with a relatively low GFA, and many exceptions can be observed in GFA characterization for this group of alloys. For example, some compositions with very high melting enthalpy △H_m are good glass forming systems, which is contrary to the results of Cai et al [23–24] who suggest a moderate △H_m for the best GFA. Also, the correlation between the GFA and the characteristic temperatures based-criteria is relatively low for this group.

In this work, the calculated viscosity at melting and the β parameter of Turnbull’s theory, combined with the calculated △H_m for nine compositions, namely Fe₄₁Co₇Cr₁₅Mo₁₄C₁₅B₆Y₂ (#1), Fe₄₈Cr₁₅Mo₁₄C₁₅B₆Y₂ (#2), Fe₆₁Co₅Zr₈Y₂Cr₂Mo₇B₁₅ (#3), Fe₈₀P₁₃C₇ (#4), Fe₇₉Si₁₀B₁₁ (#5), Fe_41.5Ni_41.5B₁₇ (#6), Fe₈₃B₁₇ (#7), Fe₉₁B₉ (#8) and Fe₈₉B₁₁ (#9), were used to study the kinetics of

glass formation in Fe-based alloys. In addition, thermodynamic parameters such as △H, the ideal entropy △S^ideal, and the mismatch term of entropy △S_σ, were investigated. Afterwards, the calculated viscosity and the thermodynamic parameters were combined to calculate the critical cooling rate of alloys. The alloy compositions above were chosen because they are Fe-based and their critical cooling rates were examined in literatures such that a reliable measure of their GFA could be available for comparison.

2 Methods

2.1 Calculation of viscosity

When melts cool down from T_m to T_g, in general, the viscosity rapidly increases approximately from 10^–3 Pa·s to 10¹² Pa·s [8]. The best model that fairly approximates the viscosity η in that range of temperature known as the Vogel-Fulcher-Tammann (VFT) equation is expressed as

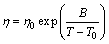                           (1)

where η₀ is a pre-exponential term, B is a constant related to the activation energy and T₀ is a constant temperature generally bellow T_g at which the configuration enthalpy is assumed to be zero. The values of T₀ were examined for many glass-forming alloys [25], but unfortunately the values could not be found in literature for most of alloys studied in this work. Sudreau and Cognet [26] used the general Andrade equation (Eq. (2)) to calculate the viscosity at melting temperature of UO₂, ZrO₂ and Zr, and they concluded that it can be an adequate model to calculate the viscosity in metal oxides. This model was tested for Fe-based alloys in this work:

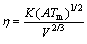                              (2)

where K is a pre-exponential constant whose value for metal oxides is 0.194×10^–6 kg^1/2×m×K^–1/2s^–1, A is the molar mass, T_m is the melting temperature, V is the molar volume, and R is the gas constant. the mean molar volume V at melting point can be calculated by Eq. (3):

                         (3)

where c_i is the molar fraction, V_i is atomic volume, A_i is atomic mass and ρ_i is the density at melting point for element i. A is defined by Eq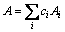. (4):

                                 (4)

Turnbull [8] proposed the relations between the nucleation rate I and η (Eq. (5)) and between the growth rate u and η (Eq. (6)):

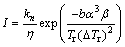                        (5)

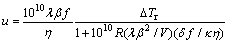         (6)

where α and β are given by Eq. (7) and Eq. (8), respectively, △T_r=(T_m–T)/T_m is the reduced undercooling, b is a constant determined by the nucleus shape, T is the absolute temperature of the system, κ is the thermo-conductivity of the liquid, △ is the distance to nucleation sink, λ is the distance that interface moves for each interfacial jump, f is the fraction of sites in the crystal surface to which molecules can be attached and V is the molar volume.

                              (7)

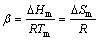                            (8)

Turnbull was able to find out the effect of the change in T_g/T_m on nucleation frequency (Eq. (5)) calculated with a simple theory, with αβ^1/3=1/2, and in his calculation, the values of viscosity from an equation of the Fulcher were calculated by Eq. (9) with constants typical of a number of simple molecular liquids and with T₀/T_m=T_g/T_m.

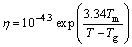                       (9)

The same way was adopted to calculate η in our calculations after modification of Eq. (9) to become Eq. (10) (in Pa×s) in order to fit the results of VFT equation (Eq. 1) for existing data from Fe-based system. The values of parameters used in calculations of viscosity taken from literatures are summarized in Table 1 as well as the characteristic temperatures and R_c of the studied compositions. Herein, the approximation of η was conducted with the guarantee of keeping GFA aspect of Fe-based alloy melts in our calculations but an extension to other alloy systems or a guarantee of full physical meaning is beyond the aim of this work.

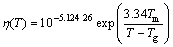                (10)

2.2 Melting enthalpy

Many attempts have been made to express the Gibbs free energy difference between liquid and corresponding crystalline phases △G^L–S as function of △H_m like it was mentioned in the work of Cai et al [23–24]. In many cases， △G^L–S is equal to a product of △H_m and a function of characteristic temperatures from calorimetric measurements (T_g, T_x and T_m), which should lead to a monotonous increase of △G^L–S as △H_m increases. However, Cai et al [23–24] demonstrated that when the main components are similar with the fitted BMGs or the additives are few enough, △H_m has a second order polynomial relation with GFA and the optimum corresponds to a moderate △H_m. The melting enthalpy of multi-component ideal solution can be calculated using Eq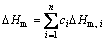. (11):

                          (11)

where n stands for the number of components and △H_{m, i} is the mole melting enthalpy of the i-th component.

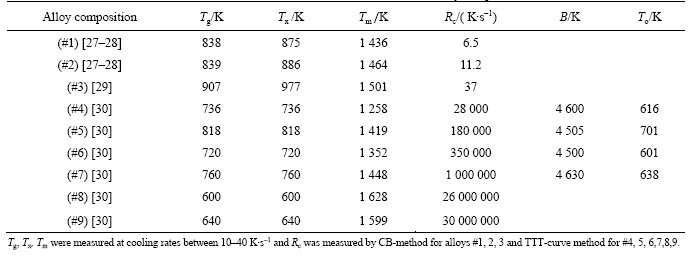
Table 1 Parameters used in this work taken from references mentioned in column of alloy compositions

.

2.3 Mixing enthalpy and entropy

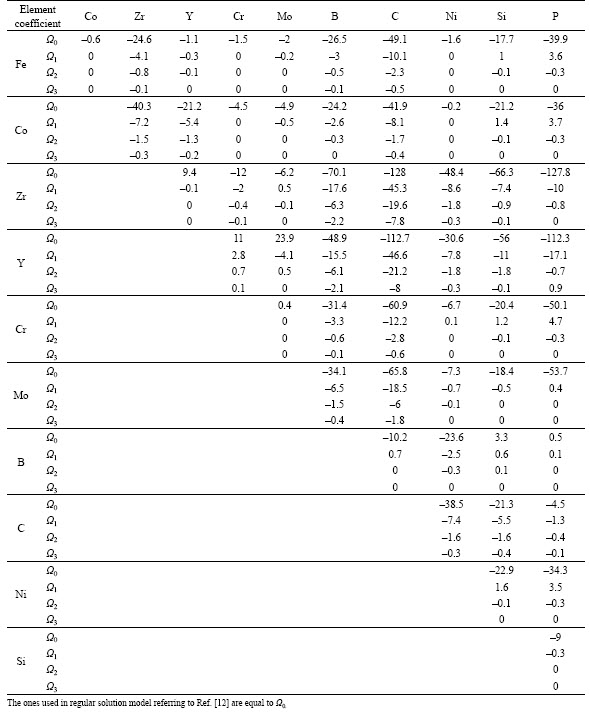
Many researchers [12–13, 31–32] have shown that the mixing enthalpy, the mismatch entropy and the configurational entropy are crucial parameters in identifying alloy compositions with better GFA, which agrees with Inoue’s conditions as well [33]. Takeuchi and Inoue [12] used a regular solution model to study GFA in metal alloys. In that model, the regular solution interaction parameters between i and j elements Ω_ij are obtained taking four times the enthalpy values of binary alloy between i and j elements at equi-atomic composition calculated by Miedema’s model which is the same as the first order interaction coefficients Ω_o in Takeuchi and Inoue sub-regular solution model [13], expressed in Eq. (12) for multi-component alloys. This sub-regular solution model is a third order polynomial approximation of the enthalpy as a function of composition indexes with interaction parameters that fit Miedema’s model. The values of interaction coefficients Ω₀, Ω₁, Ω₂ and Ω₃ of binary system used to calculate △H for studied alloy compositions were collected from the work of Takeuchi and Inoue [13] and given in Table 2 and were used to calculate △H in both models (in the regular solution model Ω_ij=Ω₀). It would be noted that in this work the notation Ω_k,ij is adopted for interaction coefficients of order k for binary system of i and j elements. △S^ideal and △S_σ were calculated as well referring to Ref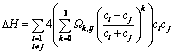. [12]:

                (12)

The kinetic and thermodynamic aspects of Fe-based alloys were combined and the values of R_c were calculated by Eq. (13) referring to Ref. [12] (Note that there is not fitting coefficient in the original form because the data we used are not the same).

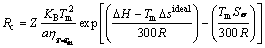 (13)

where Z is a constant of 2×10^–6, K_B is the Boltzman constant, and a is the interatomic average distance.

Table 2 Interaction coefficients Ω₀, Ω₁, Ω₂ and Ω₃ for binary systems used to calculate △H in sub-regular solution model in Eq. (12) collected from Ref. [13] (Unit: kJ×mol)

3 Results and discussion

Table 3 lists the values of viscosity at melting point calculated by different methods as well as the measured R_c for comparison. It can be seen that the values of η at melting point calculated by Andrade’s equation (Eq. (2)) are in the range of 3.5–4.3 mPa·s, which is reasonable for BMGs. However, these data are not consistent with the observed GFA. For example, even though parameters other than η are involved, high values of viscosity at T_m should correspond to the alloys with high GFA or low R_c.

Table 3 Values of viscosity at melting point calculated using different methods

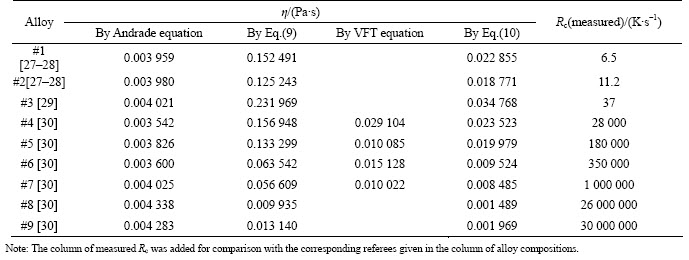
For example, Fe₉₁B₉ alloy shows the highest calculated viscosity at T_m but it is actually one of the bad glass forming alloy among the nine studied alloys. In addition, no big differences in values of the viscosity at T_m were observed between good and poor glass forming alloys, and all alloy compositions have almost the same values around 4 mPa·s.

The viscosities at melting point calculated by Eq. (9) are ranged from 9.9 to 231.9 mPa·s. These values are relatively high compared to VFT model. However, a strong inverse correlation was observed between these values of viscosity and R_c. To bring the results of the model in the normal range, a linear fitting was used to fit values obtained by this model to those obtained by VFT equation (calculated for the four alloys where values of parameters were found in literature). The right part of Eq. (9) needs to be multiplied by a linear fitting coefficient of 0.149 88 which leads to Eq. (10).

The values of viscosity calculated by Eq. (10) are also listed in Table 3. The inverse viscosity 1/η associated with Eq. (10) linearly correlates with R_c with a correlation coefficient R²=0.916. This agrees with Turnbull’s theory [8], which assumes the nucleation and growth rates to have inverse relations with viscosity.

For further understanding the error related to the approximation made in deriving Eq. (9) and Eq. (10), where the activation energy constant B in VFT equation was replaced by 3.34 times T_m, the exponent terms for both equations (term in the brackets of Eq. (10) and that of VFT equation) were examined. For the four alloy compositions whose values of B and T_m could be obtained, the ratio B/T_m oscillates between 3.6 and 3.1 independently with the increase of R_c. The average B/T_m for four alloys is 3.339 which is approximately equal to the constant used in Eq. (9). However, when the content of the main elements changes dramatically, the results may be different. For example, referring to the results of Mukherjee et al [34] for Vit1, Vit106, Vit105 and Ni_59.5Nb_40.5 alloys (reported R_c are 2, 10, 25 and 250 K/s, respectively), it can be seen that if we keep the same form of Eq. (9) but targeting same results as VFT equation, the constant 3.4 should be replaced by 9.35, 5.3, 5.5 and 3.1 for these four alloys, respectively. It is clear that for the two alloys, Vit106 and Vit105, with not much difference in their basic component elements, the coefficient does not change considerably, which agrees with the assumption we made. However, big difference can be observed between alloys with big variations in basic element contents although their differences in R_c is less than that between the above given four Fe-based alloys. Above it was mentioned that this work does not have intension to guarantee the full physical meaning of η for all alloy systems.

In Table 4, △H_m and β calculated by Eq. (11) and Eq. (8) respectively are listed. The best glass forming alloys have the highest values of △H_m and high β. Usually, both a and β parameters depend on △H_m but a decreases while β increases when △H_m increases (Eq. (7) and Eq. (8)). From Eq. (5), one can see that the crystal nucleation rate exponentially depends on –α³β=–NV²s³/RT_m(△H_m)². It is clear that considering the nucleation process, GFA should decreases as △H_m increases because of the increase in the nucleation rate. This is different from the observed data for studied Fe-base alloys in Table 4. If the glass formation is only attributed to the growth process, it can be easily shown that GFA increases with β. assuming the growth rate to be only a function of β with real positive values, the relation in Eq. (6) will be in the form of u(β)=Aβ/(1+Cβ²), where A and B are positive and independent of β. From this relation, it can be seen that for positive values of β, u(β) has a single optimum point at β=(1/C)^1/2. The limits when β tends to be zero and infinity are both zeros. This means that u(β) is an increasing function of β in the interval [0, (1/C)^1/2] and decreasing function of β in the interval [(1/C)^1/2, ∞]. For most materials, Turnbull [8] proposed that the condition K<1, where K is defined by the relation β=(K/C)^1/2, can only hold when η≥10^–1 Pa·s at melting temperature which is relatively high for Fe-based alloys then K>1 always holds for this alloy system. It follows that β=(K/C)^1/2 takes only values above (1/C)^1/2. Thus, for the studied alloy system, u(β) is a decreasing function of β and then GFA increases with increasing β when only growth process is focused on. Also, this means that the increase in △H_m, which means increase in β, increases GFA through the decrease in growth rate.

Table 4 Melting enthalpy calculated by Eq. (11), and degree of undercooling T_g/T_m and β parameter calculated by Eq. (8)

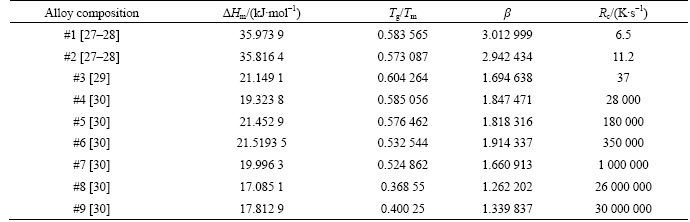
The product αβ^1/3 is used to combine both growth and nucleation processes, and high values of αβ^1/3 promote the formation of metallic glass even at low undercooling but for high values of β (β>2), therefore GFA is supposed to be dominated by growth rate limitation by the step mechanism of crystal growth demonstrated by the predominance of polyhedral, as opposed to dendritic morphology in the growth of single crystals [35]. In addition, in practice at melting temperature, the melt already contains impurities that can act as nuclei such that it is more reasonable to deal with avoiding the growth than preventing the melt from forming nuclei. Thus, it is proposed that the glass formation in Fe-base alloys is mostly realized by stopping the growth of the small nuclei in the melt. These can explain why the alloy systems with relatively high melting enthalpy are likely to have good GFA through augmentation of β-parameter which was especially observed in alloys with relatively high content of C. However, it should be understood that the parameters α and β give only information about the degree of undercooling needed for glass formation. They can not be used alone for studying the GFA. For example, it can be seen from Table 4 that Fe₄₈Cr₁₅Mo₁₄C₁₅B₆Y₂ (#2) and Fe₄₁Co₇Cr₁₅Mo₁₄C₁₅B₆Y₂ (#1) alloys have relatively small undercooling (T_g/T_m=0.573 087 and T_g/T_m=0.583 565) but with better GFA compared to Fe₆₁Co₅Zr₈Y₂Cr₂Mo₇B₁₅ (#3) (T_g/T_m=0.604 264) due to their high values of △H_m and consequent high values of β.

Calculated values of △H, △S^ideal and △S_σ referring to Ref. [12] are illustrated in Table 5. Linear relationships between the three quantities and lnR_c were observed with the linear correlation coefficients R²=0.794 9 for △H, R²=0.787 64 for △S^idealand R²=0.864 72 for calculated △S_σ. One can see from Table 5 that △H contribution terms are generally higher than those for entropy terms and this shows the importance of △H in understanding the thermodynamic view point of the GFA. The values of △H calculated by sub-regular solution model in Eq. (12) are in general greater than those calculated by the regular solution model regarded as zero order of approximation. Using the sub-regular solution model, the linear correlation with lnR_c is slightly improved (R²=0.815 62) compared to the regular solution model (R² = 0.794 9).

The results of calculated R_c (Eq. (13)) are also given in Table 5 (Eq. (10) was used for calculation of viscosity at melting, and Eq. (12) for calculation of △H). One can see that the calculated values of R_c are relatively small compared to the measured ones. However, this combination of kinetic and thermodynamic parameters allows a good categorization of GFA for alloy compositions. Figure 1 illustrates the linear correlation observed between calculated and measured lnR_c with linear correlation coefficient of R²=0.944 11. This is worth of our attention because the method can be used to order alloy composition of this group based on the GFA just using physical properties of alloying elements and calorimetric measurements. This method, even though it involves a little more calculations, is more reliable for alloys in this group than using only calorimetric measurement-based criteria like γ, γ_m, γ_C, θ, ω and others of this category as their correlation with lnR_c is relatively low for Fe-based alloy compositions. The R² correlation coefficients are 0.619, 0.716, 0.631, 0.467 and 0.758 for γ , γ_m, γ_C, θ and ω, respectively, for studied alloys compare to R²=0.94411 for calculated R_c.

Table 5 Calculated ideal entropy term △S^ideal×T_m, mismatch term of entropy △S_σ×T_m, mixing enthalpy △H calculated by regular solution model referring to Ref. [12], △H calculated by sub-regular solution model in Eq. (12) and R_c calculated by Eq. (13)

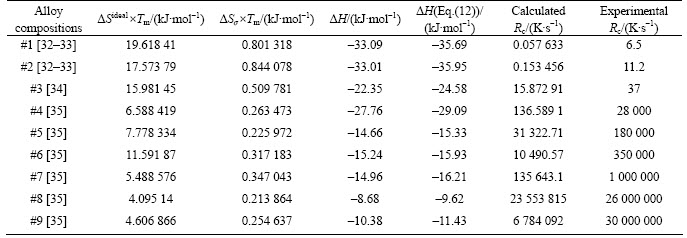
Fig. 1 Correlation between calculated and measured critical cooling rates

4 Conclusions

1) The viscosity estimated can be used to study the GFA for Fe-based alloys.

2) The growth process limitation dominates the glass formation in Fe-based alloys.

3) The addition of C in multi-component Fe-based alloys increases the melting enthalpy of alloys and then increases the chance to form glass even with a relatively low undercooling.

4) The critical cooling rate calculated on the basis of physical properties of component elements combined with calorimetric measurement data correlates better with GFA than calorimetric measurements-based criteria for the studied alloy system. It can be used to predict alloy composition with good GFA.

References

[1] ZHANG J, LIM K Y, FENG Y P, LI Y. Fe-Nd-B-based hard magnets from bulk amorphous precursor [J]. Scripta Materialia, 2007, 56(11): 943–946.

[2] TAMURA R, KOBAYASHI S, FUKUZAKI T, ISOBE M, UEDA Y. synthesis and magnetic properties of fe-b-nd-nb nanocomposite magnets [J]. Journal of Physics Conference Series, 2009, 144(1/2): 012068-(1–3).

[3] LI H X, JUNG H Y, YI S. Glass forming ability and magnetic properties of bulk metallic glasses fe68.7-xc7.0-si3.3-b5.5-p8.7- cr2.3-mo2.5-al2.0-cox (x=0–10) [J]. Journal of Magnetism and Magnetic Materials, 2008, 320(3/4): 241–245.

[4] FERENC J, ERENC-SEDZIAK T, KOWALCZYK M, KULIK T. The supercooled liquid region span of fe-based bulk metallic glasses [J]. Journal of Alloys and Compounds, 2010, 495(2): 327–329.

[5] CHIN T S, LIN C Y, LEE M C, HUANG R T, HUANG S M. Bulk nano-crystalline fe-based alloys by annealing bulk glassy precursors [J]. Intermetallics, 2008, 16(1): 52–57.

[6] CHEN Q J, SHEN J, FAN H B, SUN J F, HUANG Y J, MCCARTNEY D C. Glass-Forming ability of an iron-based alloy enhanced by co addition and evaluated by a new criterion [J]. Chinese Physics Letters, 2005, 22(7): 1736–738.

[7] CHANG H W, SHIH M F, HSIEH C C, CHANG W C. Development of bulk nd9.5fe75.5-xmxb15 (M = Mo, Nb, Ta, Ti, and Zr; x=0–4) magnets by direct casting method [J]. Journal of Alloys and Compounds, 2009, 484(1/2): 143–146.

[8] TURNBULL D. Under what conditions can a glass be formed [J]. Contemporary Physics, 1969, 10(5): 473–488.

[9] SINGH P K, DUBEY K S. Thermodynamic behaviour of bulk metallic glasses [C]// 5th International Conference on Thermophysical Properties. Baroda city, 2010, 1249: 153–156.

[10] SINGH P K, DUBEY K S. Analysis of thermodynamic behaviour of bulk metallic glass forming melts and glass forming ability [J]. Journal of Thermal Analysis and Calorimetry, 2010, 100(1): 347–353.

[11] GUO J, BIAN X F, LI X L, ZHANG C Z. Evaluation of liquid fragility for glass-forming alloys based on mixing enthalpy and mismatch entropy [J]. Intermetallics, 2010, 18(5): 933–937.

[12] Takeuchi A, Inoue A. Quantitative evaluation of critical cooling rate for metallic glasses [J]. Materials Science and Engineering a, 2001, (A304–306): 446–451.

[13] TAKEUCHI A, INOUE A. Mixing enthalpy of liquid phase calculated by miedema's scheme and approximated with sub-regular solution model for assessing forming ability of amorphous and glassy alloys [J]. Intermetallics, 2010, 18(9): 1779–1789.

[14] LU Z P, LIU C T. A new glass-forming ability criterion for bulk metallic glasses [J]. Acta Materialia, 2002, 50(13): 3501–3512.

[15] LAWS K J, GUN B, FERRY M. Influence of casting parameters on the critical casting size of bulk metallic glass [J]. Metallurgical and Materials Transactions a, 2009, 40A(10): 2377–2387.

[16] GUO S, LU Z P, LIU C T. Identify the best glass forming ability criterion [J]. Intermetallics, 2010, 18(5): 883–888.

[17] DU X H, HUANG J C, LIU C T, LU Z P. New criterion of glass forming ability for bulk metallic glasses [J]. Journal of Applied Physics, 2007, 101(8): 086108 (1–3).

[18] GUO S, LIU C T. New glass forming ability criterion derived from cooling consideration [J]. Intermetallics, 2010, 18(11): 2065–2068.

[19] ZHANG G H, CHOU K C. A criterion for evaluating glass-forming ability of alloys [J]. Journal of Applied Physics, 2009, 106(9): 094902-(1–4).

[20] YUAN Z Z, BAO S L, LU Y, ZHANG D P, YAO L, A new criterion for evaluating the glass-forming ability of bulk glass forming alloys [J]. Journal of Alloys and Compounds, 2008, 459(1/2): 251–260.

[21] ZHANG P, WEI H, WEI X, LONG Z, SU X. Evaluation of glass-forming ability for bulk metallic glasses based on characteristic temperatures [J]. Journal of Non-Crystalline Solids, 2009, 355(43/44): 2183–2189.

[22] LONG Z L, WEI H Q, DING Y H. ZHANG P, XIE G Q, INOUE A. A new criterion for predicting the glass-forming ability of bulk metallic glasses [J]. Journal of Alloys and Compounds, 2009, 475(1/2): 207–219.

[23] CAI A H, CHEN H, AN W K, TAN J Y, ZHOU Y, PAN Y, SUN G X, Melting enthalpy delta h-m for describing glass forming ability of bulk metallic glasses [J]. Journal of Non-Crystalline Solids, 2008, 354(15/16): 1808–1816.

[24] CAI A H, CHEN H, AN W K, TAN J Y, ZHOU Y. Relationship between melting enthalpy delta h_m and critical cooling rate r_c for bulk metallic glasses [J]. Materials Science and Engineering 2007,457(1/2): 6–12.

[25] TAKEUCHI A, KATO H, INOUE A. Vogel-fulcher-tammann plot for viscosity scaled with temperature interval between actual and ideal glass transitions for metallic glasses in liquid and supercooled liquid states [J]. Intermetallics, 2010, 18(4): 406–411.

[26] SUDREAU F, COGNET G. Corium viscosity modelling above liquidus temperature [J]. Nuclear Engineering and Design, 1997, 178(3): 269–277.

[27] PONNAMBALAM V, POON S J, GARY J S. Fe-Based bulk metallic glasses with diameter thickness larger than one centimeter [J]. Journal of Materials Research, 2004, 19: 1320–1323.

[28] SHEN J, CHEN Q J, SUN J F, FAN H B, WANG G. Exceptionally high glass-forming ability of an fecocrmocby alloy [J]. Applied Physics Letters, 2005, 86(15): 151907-(1–3).

[29] CHEN Q J, FAN H B, SHEN J, SUN J F, LU Z P, Critical cooling rate and thermal stability of Fe-Co-Zr-Y-Cr-Mo-B amorphous alloy [J]. Journal of Alloys and Compounds, 2006, 407(1/2): 125–128.

[30] DAVIES H A. Rapidly quenching and formation of metallic glasses [C]// Proc Rapidly quenched metals III. Brighton, 1978: 1–23.

[31] BHATT J, MURTY B S. Thermodynamic modeling of zr-ti-cu-ni-be bulk metallic glass [J]. Transactions of the Indian Institute of Metals, 2009, 62(4/5): 413–416.

[32] BASU J, MURTY B S, RANGANATHAN S, Glass forming ability: miedema approach to (Zr, Ti, Hf)-(Cu, Ni) binary and ternary alloys [J]. Journal of Alloys and Compounds, 2008, 465(1/2): 163–172.

[33] INOUE A, Stabilization of metallic supercooled liquid and bulk amorphous alloys [J]. Acta Materialia, 2000, 48(1): 279–306.

[34] MUKHERJEE S, SCHROERS J, ZHOU Z, JOHNSON W L, RHIM W K. Viscosity and specific volume of bulk metallic glass-forming alloys and their correlation with glass forming ability [J]. Acta Materialia, 2004, 52(12): 3689–3695.

[35] DOREMUS B W, ROBERT H, ROBERTS, TURNBULL D. Growth and Perfection of Crystals [M]. New York: Wiley, 1958.

(Edited by HE Yun-bin)

Foundation item: Projects(51174094, 51101059) supported by the National Natural Science Foundation of China

Received date: 2012-03-05; Accepted date: 2012-07-07

Corresponding author: Liu Zhong-wu, Professor, PhD; Tel: +86–20–22236906; E-mail: zwliu@scut.edu.cn