DOI： 10.11817/j.issn.1672-7207.2019.10.015

流-固-化耦合条件下硬脆性泥页岩井壁渐进破坏效应探讨

肖志强¹,贾善坡^{1, 2},亓宪寅^{1, 3},戴永浩³,吕方⁴,贾陆锋¹,温曹轩¹

（1. 长江大学 岩土力学与工程研究中心，湖北 荆州，434023；

2. 东北石油大学 非常规油气研究院，黑龙江 大庆，163318；

3. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉，430071；

4. 湖北省油田化学产业技术研究院，湖北 荆州，434000）

摘要:通过对硬脆性泥页岩理化性能、微观结构和力学特性等室内试验和现场测试结果的分析，探讨泥页岩井眼失稳机制，在综合考虑泥页岩吸水扩散、压力传递、强度弱化以及固体变形之间相互耦合效应的基础上，建立泥页岩井壁稳定渗流-应力-化学耦合数学模型，并且根据修正的Drucker-Prager 破坏准则，以ABAQUS软件为求解器，编制计算程序，然后应用提出的耦合数学模型模拟了硬脆性泥页岩地层中井眼破坏的动态演化过程。研究结果表明：不同钻井液当量密度下井眼扩大率随着钻井液当量密度的增大而减小，适当的提高钻井液当量密度，有利于井壁保持稳定。若不考虑泥页岩水化效应，井眼钻开后便趋于稳定，渗流场的变化并不足以引起井眼继续破坏，而考虑泥页岩水化效应后，井眼扩大率随钻井液浸泡时间的增大而增大，水化效应对井眼扩大率的影响远大于渗流场，计算出的井眼渐进破坏过程与实际钻井情况基本一致。

关键词:硬脆性泥页岩；水化；井壁稳定；钻井液浸泡；渐进破坏

中图分类号:TE28    文献标志码:A     文章编号:1672-7207（2019）10-2464-17

Hydraulic-mechanical-chemical coupling evaluation for progressive failure of hard brittle shale wellbore

XIAO　Zhiqiang¹, JIA　Shanpo^{1, 2}, QI　Xianyin^{1, 3}, DAI　Yonghao³, LU　Fang⁴, JIA　Lufeng¹, WEN　Caoxuan¹

(1. Geotechnical Mechanics and Engineering Research Center, Yangtze University, Jingzhou 434023, China；

2. Institute of Unconventional Oil & Gas, Northeast Petroleum University, Daqing 163318, China；

3. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China；

4. Hubei Oilfield Chemical Industry Technology Research Institute, Jingzhou 434000, China)

Abstract: Through the analysis of laboratory tests and field test results of physical and chemical properties, microstructure and mechanical properties of hard brittle shale, and the mechanism of shale wellbore instability were discussed. Based on the comprehensive consideration of the mutual coupling effect between the shale water absorption and diffusion, pressure transmission, strength weakening and solid deformation, a hydraulic-mechanical-chemical coupling mathematical model was established for wellbore in hard brittle shale. According to the modified Drucker-Prager failure criterion, the calculation program was compiled with ABAQUS software as the solver, and then the proposed coupled mathematical model was used to simulate the dynamic evolution process of wellbore failure in hard brittle shale formation. The results show that the wellbore enlargement rate decreases with the increase of drilling fluid equivalent density, and the proper increase of drilling fluid equivalent density is beneficial to the stability of the wellbore. If the shale hydration effect is not considered, the wellbore tends to be stable after excavation, and the change of the seepage field will not cause the wellbore to continue to be damaged. After considering the shale hydration effect, the wellbore enlargement rate increases with the immersion time of drilling fluid. The effect of hydration effect on the wellbore enlargement rate is much larger than the seepage field. The calculated progressive failure process of the wellbore is basically consistent with the actual drilling.

Key words: hard brittle shale; hydration; wellbore stability; drilling fluid immersion; progressive failure

中深层勘探开发是东部油田近年勘探开发的重点，因其埋藏深，岩性水敏性强，裸眼浸泡时间长，同时存在裂缝，加剧了井壁失稳，使中深层硬脆性泥页岩的井壁稳定成为制约钻速的瓶颈^[1-3]。因此，从降低钻井成本以及加快油气田勘探开发的角度出发，对泥页岩井壁稳定性问题进行深入的研究具有非常重要的意义。NP凹陷属于典型的陆相淡水湖泊沉积盆地，形成了半深湖-深湖相暗色泥页岩和油页岩等优质烃源岩，主力烃源岩为沙河街组岩性圈闭，埋藏深度超过4 000 m，发育着几百米的硬脆性泥页岩。沙河街组硬脆性泥页岩黏土矿物含量较高、微裂缝发育，在实钻过程中，压差渗透、裂缝自吸水及长时间浸泡引发的泥页岩水化效应显著，剥落掉块，导致井径变化较大，经常造成钻具阻卡、电测遇阻等井下复杂情况，严重影响钻井效率。地层原有的力学平衡及化学平衡，在井眼钻开后便被打破，由于液压梯度和化学梯度的共同作用，导致了井壁围岩浸泡区的出现，渗流扩散效应和钻井液对泥页岩的水化作用，使得浸泡区围岩成为了随着时间而变化的非均质体，这一系列的影响导致了泥页岩井壁经历了一个非常复杂的过程。针对泥页岩井壁稳定性的研究，国内外学者已经开展过很多工作，但由于研究方向的不一致以及问题的高度复杂性，导致了研究成果的不一致，并且每一种理论都有其一定的局限性。YEW等^[4]将泥页岩水化膨胀应力比拟为热膨胀变温应力，将水向页岩中的运动比拟成热扩散。根据热弹性力学理论，对泥页岩水化产生的力学效应建立了定量化模型。该理论模型考虑了含水量的变化对泥页岩井壁稳定的影响效应，但是忽略了泥页岩与钻井液之间化学作用的本质；张乐文等^[5-6]应用半透膜等效孔隙压力理论研究了泥页岩与水基钻井液之间的相互作用，建立了泥页岩地层井壁稳定的力化耦合模型，但是该研究未考虑离子扩散和离子交换对泥页岩水化的影响；HEIDUG等^[7-9]建立的泥页岩吸水膨胀耦合模型，该模型较全面地研究了井壁稳定的力学-化学耦合效应，但没有考虑到流体孔隙压力与岩石变形之间的联合作用；CHEE等^[10-13]在综合考虑泥页岩-钻井液体系中的电化势、离子运移和流体流动、溶质扩散过程的非线性以及流体流动和离子运移对固体变形影响的基础上，建立了泥页岩井壁稳定流-固-化耦合模型，但是该模型中存在着很多难以确定的参数，不方便实际应用，同时也未考虑到地层钻井卸载以及塑性变形。泥页岩地层一经钻开，便打破了其原有的平衡状态，井壁围岩参数会随着与钻井液接触的时间变化而发生变化。因此，一个有效的井眼预测模型应该使发生在泥页岩地层中的力学以及物理化学动态过程得到体现。NP凹陷W号构造为岩性圈闭，其埋藏深度为3 800~4 500 m。东二段至沙河街井段中钻遇到层理和微裂隙都比较发育的大段硬脆性泥页岩，在钻井过程中表现为易塌、易漏等复杂情况，导致该地区的钻井效率被严重制约。本文作者总结前人的研究成果，并对硬脆性泥页岩理化性能、微观结构以及力学特性进行分析，解释其失稳机理。为了探索井眼破坏的演化规律，通过考虑钻井过程中岩石的实际卸载过程、强度弱化以及塑性变形的特性，建立了泥页岩井眼渐进破坏耦合模型，从机理上提高了保持硬脆性泥页岩井壁稳定的认识，为钻井液的优选提供参考依据。

1 泥页岩组成及理化性能试验

在实钻过程中，沙河街组泥页岩井径变化较大，井壁失稳问题突出。因此，需要对泥页岩的岩性、矿物组成、微观结构及水化等方面开展测试研究。

1.1　地层矿物组成

利用X线衍射仪，对W号构造3口井沙河街组泥页岩段岩芯进行全岩矿物和黏土矿物分析，全岩矿物和黏土矿物组成与质量分数如表1和表2所示。

从表1和表2可以看出：沙河街组泥页岩的矿物主要为黏土和石英，另外不同程度地发育着长石、方解石、白云石等，脆性矿物(石英、长石和方解石)较为发育，其中石英质量分数为6.71%~39.94%；黏土含量整体较高，其质量分数为19.09%~43.06%，黏土矿物中较为发育的主要为伊利石以及伊/蒙混层，沙河街组矿物中均未见蒙脱石的发育，其中伊利石质量分数为34.47%~56.64%，伊/蒙混层质量分数为6.72%~39.74%。

表1　全岩矿物组成与质量分数

Table 1　Mineral composition and mass fraction of shale

表2　黏土矿物种类及质量分数

Table 2　Types and mass fraction of clay minerals

1.2　泥页岩细观构造

探究黏土矿物晶体的定向排列、胶结结构以及微裂隙的发育和分布状况要从泥页岩的微观结构入手。目前研究岩石内部微裂缝等微观结构普遍所采用的有效手段是利用环境扫描电镜进行观察。利用扫描电镜分析W号构造沙河街组泥页岩微观构造和黏土矿物赋存形态，扫描结果如图1所示。

从图1可以看出：W号构造沙河街组泥页岩内部微裂缝、微孔洞等发育程度较高，微裂缝以及微孔洞的发育一方面破坏了泥页岩的结构完整性，弱化原岩的力学性能，另一方面也为钻井流体侵入地层提供了流动通道。钻井流体通过这样的通道侵入地层不仅可能诱发水力劈裂作用促使井眼加剧破坏，更重要的是与地层中的黏土矿物以及有机质等发生作用，造成井壁坍塌等事故。

图1　W-82井泥页岩岩芯扫描电镜图像

Fig. 1　SEM images of shale core in well W-82

1.3　钻井液体作用对泥页岩结构的影响

泥页岩中的黏土矿物在遇到水的情况下，会发生水化膨胀的现象，沙河街组泥页岩黏土矿物中以伊利石以及伊/蒙混层较为发育，蒙脱石晶层间的连接力很弱，因此，能在其晶层间以及颗粒外表面进行水化作用，水化膨胀性很强，而伊利石晶层间的连接较紧密，水化膨胀仅能发生在颗粒外表面，水化膨胀性相对较弱，各种黏土矿物的水化膨胀能力由大到小排序为：蒙脱石，伊/蒙混层，伊利石，高岭石，绿泥石。可见：不同黏土矿物的水化膨胀能力不同，以至于不同的黏土矿物遇水后吸水膨胀速率相差很大，进而产生相差很大的膨胀压力；再者钻井流体会使微裂缝尖端产生应力集中，这些因素的存在很可能导致泥页岩的最终破坏。

采用高倍偏光显微镜观察泥页岩在流体作用后细观结构的变化。图2和图3所示分别为清水及水基钻井液作用下，高倍偏光显微镜下观察到的岩样结构变化及微裂缝的形态特征。可见：清水、钻井液侵入前的岩样结构较为致密、完整，而经过清水、钻井液一段时间的作用后，泥页岩表面发生了变化，这是泥页岩内部微裂纹的萌生、扩展以及分叉所导致的结果，从而进一步破坏了原岩的完整性以及弱化原岩的力学性能，并且清水、钻井液还将沿微裂缝侵入到泥页岩的内部，与泥页岩发生水化作用进一步破坏泥页岩的结构，加剧井壁的破坏。

图2　清水沿微裂缝侵入

Fig. 2　Clear water intrusion along micro-cracks in shale

图3　钻井滤液作用下的微裂缝形态变化

Fig. 3　Morphological changes of micro-cracks under action of drilling filtrate

1.4　阳离子交换容量

阳离子交换即阳离子交换性吸附，是泥质岩重要特征之一，阳离子交换容量是指黏土矿物的表面可用于交换阳离子的数量。泥页岩的阳离子交换容量是全部黏土矿物阳离子交换的总和。阳离子的交换容量越大，表示黏土能够携带的负电荷越多，越能从周围的介质中吸附更多的阳离子来中和多余的负电荷，即阳离子交换容量越大越有利于泥页岩表面水化。因此，可以利用阳离子的交换容量，来预测地层潜在的水敏性。黏土在水中分散时，吸附的阳离子要从黏土表面扩散，泥页岩地层中黏土矿物的含量较大，通过测定泥页岩的阳离子交换容量(CEC)，可以反映出泥页岩的水化、膨胀和分散能力，是评价地层水化膨胀能力的重要依据。

对泥页岩岩样处理后测定阳离子交换容量，W号构造沙河街组泥页岩的阳离子交换容量分布范围为90~235 mmol/kg，平均为146.25 mmol/kg，表明沙河街组泥页岩具有一定的水化能力，水基钻井液作用下易发生井下失稳。

2 钻井液对泥页岩力学性质影响试验

泥页岩的力学特性是影响井眼稳定性的重要因素。由于硬脆性泥页岩的水化特性显著，在对其进行钻井时，对钻井液具有很高的要求，钻井液的优选对保持硬脆性泥页岩地层的井壁稳定起着决定性的作用

2.1　原岩力学特性

考虑到泥页岩的水敏性，针对钻井岩芯进行干冰冷冻，采用液氮冷却钻头，钻取试验所用岩样。取自W-82井沙河街组泥页岩岩芯进行原岩三轴压缩力学特性测试，三轴应力应变曲线如图4所示，泥页岩弹性模量为18.27~23.59 GPa，泊松比为0.12~0.23，内聚力为24.14 MPa，内摩擦角为21.7°。另外，对5个沙河街组岩样进行了巴西劈裂试验，抗张强度为1.13~6.09 MPa，平均值为4.41 MPa。

脆性是岩石的一种固有力学特性，并受岩石组分、结构以及围压、温度等因素的影响、控制。目前，岩石矿物组分及弹性参数是石油工程领域应用较为广泛的2种岩石脆性评价指标：基于岩石矿物组分的脆性评价和基于岩石弹性参数的脆性评价。参考贾善坡等^[14-15]的研究成果，基于脆性矿物的泥页岩脆性评价结果为：W-82井沙河街组泥页岩脆性指数为0.664，W-96井沙河街组泥页岩为0.809，W-81井沙河街组泥页岩为0.569。

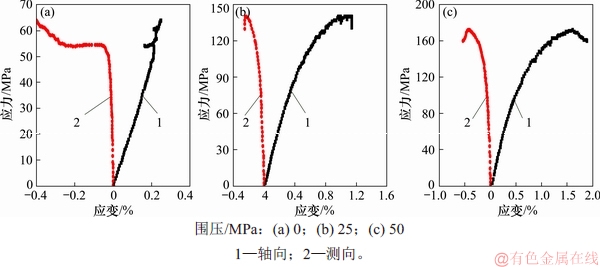
图4　W-82井泥页岩原岩三轴试验结果(深度为4 150 m)

Fig. 4　Triaxial test results of original rock in W-82 well (depth of 4 150 m)

RICKMAN等^[16]在对北美地区泥页岩的弹性模量、泊松比进行统计的基础上，考虑弹性模量越大，泊松比越小，则脆性越大，提出了利用弹性模量和泊松比2个参数表征岩石的脆性强弱。利用上述泥页岩的三轴压缩测试分析结果：岩芯1号(围压为0 MPa)对应的脆性指数为0.424，岩芯2号(围压为25 MPa)为0.367，岩芯3号(围压为50 MPa)为0.326。表明该区的泥页岩呈现出较高的脆性。

2.2　钻井液体作用对泥页岩力学性质的影响

为探究泥页岩力学性质在钻井液作用下的变化规律，为钻井液保持岩石强度性能的评价提供依据，开展了工区在用钻井液作用下岩石力学特性测试。

由于泥页岩钻井岩芯获取困难，且用于开展三轴试验的有效岩芯非常有限，采用史氏压入硬度法测试钻井液对泥页岩压入硬度影响。硬度反映了岩石抵抗工具侵入破坏的能力，压入硬度试验对岩样形状的要求较直剪试验和三轴压缩试验低，便于大量进行测试分析。

表3　压入硬度随着钻井液浸泡时间的变化

Table 3　Change of indentation hardness with drilling fluid immersion time

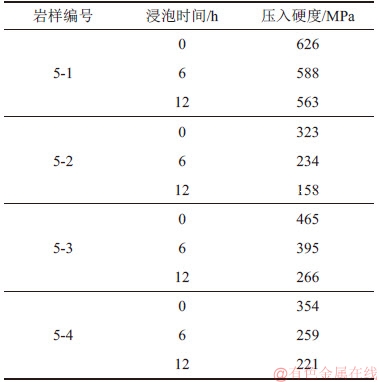
将泥页岩浸泡在钻井液中，通过测试不同浸泡时间下泥页岩的压入硬度，描述泥页岩强度的变化特征。选取同一位置泥页岩分别开展原岩、浸泡钻井液6 h和12 h的压入硬度试验，共开展4组，试验结果如表3所示。从表3可以看出：随着浸泡时间的增加岩样的压入硬度逐渐降低，并且浸泡时间越长压入硬度降低越明显，这些规律表明了钻井液对其强度的影响不可忽略。

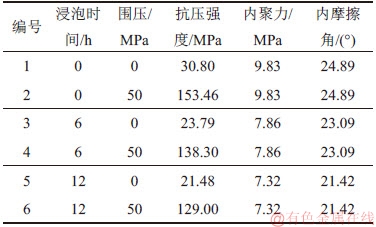
由于该工区岩芯短缺，对邻区同层位泥页岩进行了测试分析，结果表明：在对岩样进行浸泡的过程中，沙河街组样品的完整性被破坏，发现有宏观裂缝产生，部分岩样破碎成碎块，水化程度较为严重。分别进行泥页岩在钻井液中浸泡0 h(原岩)，6 h和12 h后的单轴和三轴压缩试验，试验结果如表4所示。从表4可知：在同一围压下，随着硬脆性泥页岩在钻井液中浸泡时间的增加，其力学强度逐渐降低，浸泡6 h后强度平均降低16.32%，浸泡12 h后强度平均降低23.10%。

表4　钻井液浸泡作用下泥页岩强度变化

Table 4　Shale strength changes under drilling fluid immersion

3 泥页岩井眼破坏流-固-化耦合模型

综合上述对泥页岩理化性能和力学特性试验分析结果可知，导致该区钻井过程中井壁失稳的主要因素有以下几点：一是泥页岩黏土含量较高且黏土矿物中伊/蒙混层较为发育，作为膨胀性与非膨胀性黏土相间的矿物，较易吸水致使非均匀性水化膨胀，类似的规律通过阳离子交换试验再次证明，该区的泥页岩易与外来流体发生水化作用，减弱泥页岩结构强度。二是沙河街组泥页岩内部微裂隙和微孔洞较为发育，提供了外来流体侵入泥页岩内部的通道以及水化作用的空间，造成岩石强度降低，增加井壁坍塌风险。三是W号构造沙河街组泥页岩脆性相对较强，在钻井过程中的应力释放(卸荷)、井筒压力波动、机械钻速低或浸泡时间长更易导致井壁岩石破裂，为钻井液侵入提供通道，诱发、加剧井壁垮塌。因此，研究泥页岩井眼渐进破坏动态演化时须考虑钻井液在地层中的扩散与渗透以及岩石的强度弱化行为^[17]。

3.1　吸水扩散模型

泥页岩在井眼钻开后便与钻井液接触，受到水力梯度和化学势梯度的驱动，引起了水和离子的相互传递。泥页岩的吸水过程十分复杂，这里令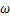表示吸附水量的质量分数，它随着时间和空间而发生变化，依据质量守恒方程建立了水分的扩散方程^[18]：

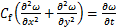(1)

式中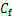：为泥页岩吸水扩散系数。吸水扩散系数表征了地层水变化传递的速度，可通过泥页岩吸水扩散试验测得。相应的边界和初始条件按照远场以及井壁的含水量来确定。

3.2　压力传递模型

考虑到泥页岩的半透膜特性，化学势差的存在会促使钻井液中的一些离子发生运移，导致了地层的水活度发生改变。活度指的是盐溶液和纯水的逸度比，表征了溶液中化学势的强弱，钻井过程中地层流体的活度计算模型为^[19]

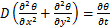(2)

式中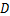：为活度扩散系数。活度扩散系数表征了地层水活度传递的快慢，可以通过页岩的压力传递试验数据拟合得到。

地层的孔隙压力在钻井液进入地层后，受到地层流体与钻井液之间的化学势差和水力压差的共同作用而重新分布。在综合考虑了化学势差和流体的流动之后，建立了孔隙压力的计算模型^[20-21]：

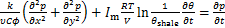(3)

式中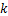：为泥页岩的渗透率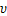；为流体黏度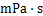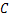，；为流体的压缩系数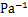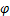，；为孔隙度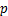；为地层的流体压力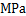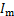，；为膜效率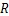；为气体常数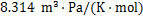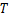，；为热力学温度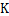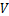，；为水的偏摩尔体积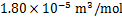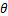，；为钻井过程中地层流体活度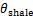；为泥页岩中地层水活度。

3.3　井眼破坏模型

有效应力可根据Biot有效应力原理，表示如下：

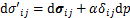(4)

式中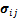：为总应力张量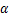；为Biot系数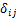；为Kronecker符号。

根据已建立的压力传递模型并结合有效应力原理以及弹塑性力学理论^[22]，建立综合考虑化学势变化、流体流动与骨架变形耦合的本构方程，表示如下：

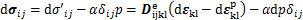(5)

式中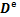：为弹性刚度张量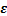；为总应变张量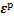；为塑性应变张量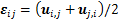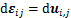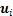；，；为岩石骨架的位移分量。

考虑到泥页岩的实际抗拉能力，井眼的破坏准则采用的是修正的Drucker-Prager准则(简称D-P准则)。针对于拉剪型的应力状态，常规的D-P准则不适用，它只是考虑了压剪型的应力状态，而在拉剪区将会失去实验基础，高估了岩石的抗拉能力。当采用过平衡钻井方式时，由于井底的压力高于地层压力，在井眼处可能会有拉剪型应力状态的出现，故而有必要对常规D-P准则进行修正，修正后的D-P准则示意图如图5所示。基于贾善坡等^[23]的修正思想，采用Rankine最大拉应力准则对常规的D-P准则进行修正，屈服函数表达式为

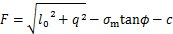(6)

式中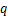：为Mises应力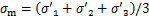；为有效围压应力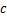；为岩石黏聚力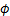；为岩石内摩擦角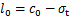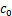；，为原岩黏聚力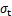，为岩石抗拉强度。

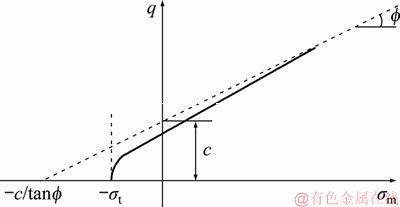
图5　修正的Drucker-Prager准则

Fig. 5　Modified Drucker-Prager criteria

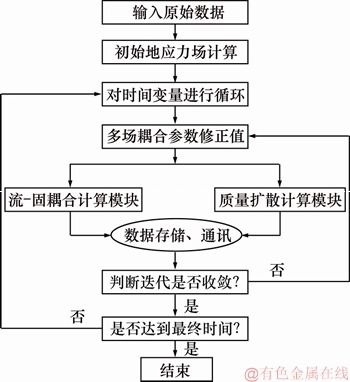
图6　多场耦合程序系统程序结构

Fig. 6　Flowchart of multifield coupling code

从式(6)可知：若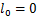，修正过后的D-P准则就变为了原D-P准则。修正过后的D-P准则处处都是光滑的，是一个正则屈服准则且便于数值的计算。

泥页岩的强度参数随着地层含水量而发生变化，结合相关试验成果^[21]可知，强度参数的变化趋势近似是随着含水量动态线性衰减，将式(1)和式(6)进行耦合，可建立水化泥页岩强度弱化动态模型，即：

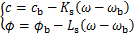(7)

式中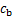：为当含水量为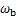时的黏聚力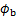；为当含水量为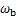时的内摩擦角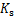；为黏聚力系数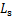；为内摩擦角系数。

3.4　模型的数值实现

基于上述分析，本文通过采用解耦的数值处理方法，首先针对相对独立的水分扩散方程进行求解，然后将压力传递模型与固体变形进行间接协同耦合进行求解，整个过程涉及到ABAQUS软件内嵌的2个计算模块，也就是岩土固结模块和质量扩散模块。

虽然岩土介质的流-固耦合场与质量扩散场在数值计算上表现为较大的差异性，但究其本质两者都是包含了线性化与时步离散(或载荷增量)2个基本内容，也就是将流-固体场和扩散场按照2个独立的系统分别进行设计、计算，每一时步上的参数耦合是通过数据通讯的方式进行实现，不断地在每一时步上修正相关的系数，并且这种相互修正是在一系列的时步上交叉进行的。在贾善坡等^[24-25]的研究基础上，以MATLAB为平台，ABAQUS为求解器，开发了计算泥页岩井眼动态破坏的软件，通过编制ABQMAIN子程序实现各个计算模块之间数据的存储和通讯，强度参数的弱化则是通过USDFLD子程序来进行实现，程序的流程见图6。

4 实例分析

本文以欠平衡钻井方式下钻开地层为例，分析是否考虑水化作用对井眼渐进破坏的影响规律。

4.1　工程概况

W号构造位于渤海湾盆地黄骅坳陷NP凹陷的西部，是重要的勘探区带，已钻遇地层自下而上依次为古近系沙河街组、东营组，新近系馆陶组、明化镇组和第四系平原组。W号沙河街组岩性圈闭，面积为356 km²，最大厚度为840 m，闭合幅度为1 000 m，上覆沙一段大套泥页岩可作为良好盖层，有利于形成自生自储的大型岩性油气藏。

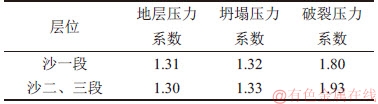
依据钻井井史、钻井液总结报告及完井卡片，对该区内已钻的20余口井目标层井下复杂情况进行统计，分析表明：井下复杂情况以井漏现象最为突出，其次为井眼掉块、坍塌，井漏发生次数约为井壁失稳的4倍，目标层位地层破裂压力系数大都在1.80以上(表5)，井下复杂井段所用钻井液当量密度最大为1.6，结合岩芯观察和成像测井资料，井漏段地层井周裂缝较为发育，提高钻井液当量密度，对井壁垮塌、扩径的抑制效果不理想，部分井的钻井液当量密度由1.23提高至1.39时，井径反而增大。

沙河街组硬脆性泥页岩发育微裂缝，同时存在部分微孔洞，这些孔缝为钻井滤液侵入地层内部提供通道，加之地层黏土含量较高，常规钻井过程中滤液的侵入或自吸水的发生容易引起水化膨胀，再加上高渗流能力裂缝的存在，使常规钻井过程中容易出现井漏等钻井问题。为避免或减少在钻井过程中出现相关的问题，实施欠平衡钻井方式是解决上述有关问题的有效途径。从表5可知：沙河街组地层压力系数高于1.3，故欠平衡钻井循环钻井液选用水基钻井液体系。本文以W-82井为研究对象，该井上覆无海水，井深为4 745 m，钻遇地层主要为明化镇组、馆陶组、东营组和沙河街组地层，用于勘探W号构造沙河街组岩性圈闭含油气情况，四开采用液相欠平衡钻井技术，欠平衡钻进于4 146.93~4 745.00 m，欠平衡进尺为598.07 m。

表5　W号构造地层压力测试结果

Table 5　Pressure test results of W structural formation

4.2　计算模型及参数

为模拟沙河街组4 250 m附近井眼稳定性，对模型进行离散采用的是平面应变四边形单元，由于井眼的对称性，有限元计算模型取为井眼的1/4，模型长为15 m，长宽比为1:1，模型的中央是井眼，井眼半径为0.108 m。利用渐变网格技术实现对井眼及模型中间线的局部加密，划分的网格如图7所示，网格总数为1 993，节点总数为2 087。

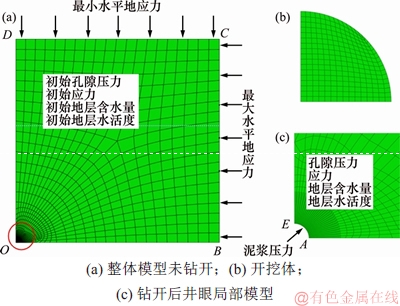
图7　网格划分

Fig. 7　Meshes of analysis model

定义模型边界条件为：在BC边施加最大水平地应力，CD边施加最小水平地应力；OB边为水平滑移边界，OD边为垂向滑移边界；在模型的内部定义初始孔隙压力、初始应力、初始地层含水量、初始地层水活度；地层钻开之后，AE边施加井眼液柱压力、含水量条件、钻井液活度条件，并根据钻井液活动设置渗流边界条件(定义渗透压力)。

通过有限元软件模拟井眼渐进破坏过程的计算步骤如下：第一阶段为地应力平衡阶段，该阶段是为了还原初始应力场也就是地层钻开之前的应力状态，通过定义模型内部与外部的应力场，使得还原的初始地应力场符合计算的要求；第二阶段为钻井阶段，本阶段是为了模拟井眼的钻开，通过单元生死，并施加泥浆压力模拟钻井过程(地层被钻开)，由于该步的时间比较短，并且考虑到泥页岩的渗透性较低，该步不考虑井壁的渗透性；第三阶段为渗流扩散阶段，本阶段是为了模拟井筒内、外发生的渗流扩散效应，井眼围岩强度因水化而被减弱，模拟了井眼钻开完成后53 d内井壁的破坏过程。

根据室内试验、现场资料、测井资料以及邻区地质资料获得计算所需基本参数：上覆岩层压力为91.63 MPa，水平最大地应力为81.22 MPa，水平最小地应力为68.72 MPa，地层压力系数为1.3，地层弹性模量为20.2 GPa，泊松比为0.16，黏聚力为24.1 MPa，内摩擦角为21.7°；根据测井解释，地层渗透率为(0.13~12.56)×10^-3 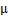m²，孔隙度为8.00%。实际钻井液当量密度为1.2，活度扩散系数为5×10^-9 m²/s，地层吸水扩散系数为9.5×10^-9 m²/s；初始地层含水量为2%，饱和含水量为10%。

4.3　不考虑水化情况下的计算结果

为了区分泥页岩渗流和水化扩散对井眼破坏的影响机制，暂不考虑两者的耦合，这里仅探讨渗流对井眼稳定性的影响。

采用欠平衡钻井方式打开地层，以钻井液当量密度为1.0，1.1，1.2和1.3为例，对上述计算模型进行数值模拟，探讨井眼坍塌破坏过程，地层钻开后井眼破坏区分布如图8所示。

从图8可知：井眼在平行最小地应力方向发生剪切破坏，在这一方向尺寸变大，破坏区为近似的椭圆形状，与井下成像观测和室内试验结果一致。钻井液当量密度越大，塑性区越小，适当提高钻井液当量密度，有利于井壁保持稳定。地层钻开数天后，井眼破坏程度并没有发生任何变化。

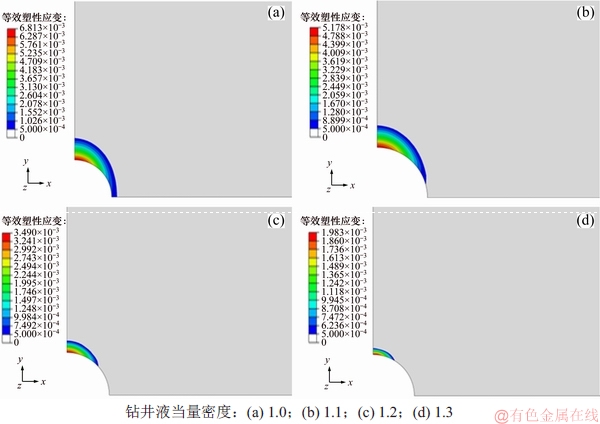
图8　钻开后井眼破坏云图分布

Fig. 8　Distribution of cloud damage in wellbore after excavation

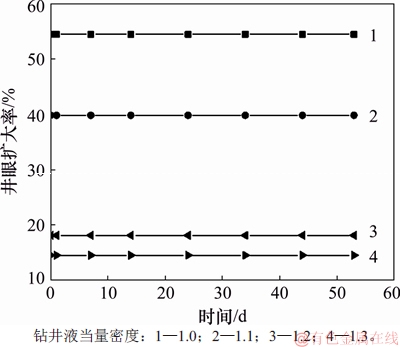
图9　不考虑水化作用下的井眼扩大率随时间变化曲线

Fig. 9　Curve of wellbore enlargement rate with time under without considering hydration

不考虑泥页岩水化影响，井眼扩大率随时间的变化曲线如图9所示。从图9可知：井眼扩大率随着钻井液当量密度的增大而减小，当钻井液当量密度为1.2时，钻开瞬间井眼扩大率在20%以内，随着时间的增加井眼并没有继续扩大。由此可以说明，不考虑水化效应时，井眼钻开后便趋于稳定，钻开初期，渗透压力的梯度较大，渗流场的变化会引起应力场的变化，尽管渗流场的变化会引起应力场的变化，但其变化程度较小，并不足以引起井眼的继续破坏。

图10所示为钻井液当量密度为1.2时，地层钻开后井壁孔隙压力分布图。从图10可知：孔隙压力随着距井壁距离的增大而逐渐增大并趋于初始孔压，其变化速率随钻开时间的增大而减小，钻开井眼1 d后，渗流场的扰动范围约为10倍的井眼半径，钻开井眼53 d后的扰动范围约为50倍的井眼半径。

根据上述分析可知，对硬脆性泥页岩地层实施欠平衡钻井来说，钻井初期出现井壁坍塌等钻井问题的主要原因是钻井液所能提供的液柱压力不能达到地层支撑的压力。为此在欠平衡钻井过程中，应减少循环和压力波动，保证欠平衡钻井的顺利进行。

4.4　考虑水化情况下的计算结果

图11所示为钻井液当量密度为1.2时，地层钻开后井壁孔隙压力分布图。从图11可知：孔隙压力随着距井壁距离的增大而逐渐增大并趋于初始孔压，其变化速率随钻开时间的增大而减小，这与不考虑水化影响所得出的规律一致，不同的是考虑水化的情况下，扰动区域的范围更大，增加的这一部分便是由于水化扩散的影响。

图12所示为钻井液当量密度为1.2时，地层钻开后井眼围岩含水量分布图。从图12可知：含水量随着距井壁距离的增大而逐渐减小并趋于最小值2%，地层钻开后早期，含水量变化较为剧烈，存在一定的波动，此后含水量变化速率随浸泡时间的增大而减小。

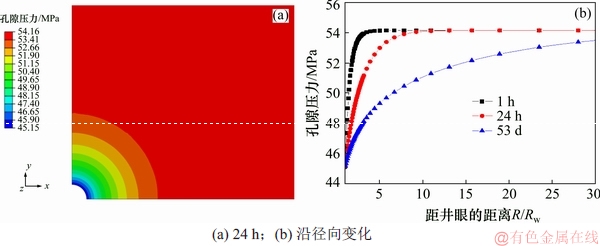
图10　不考虑水化作用下地层钻开后井壁孔隙压力分布

Fig. 10　Pore pressure distribution of wellbore after drilling without considering hydration

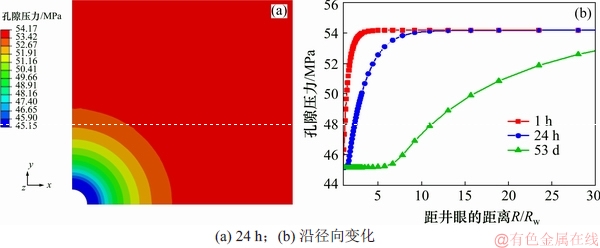
图11　考虑水化作用下地层钻开后井壁孔隙压力分布

Fig. 11　Pore pressure distribution of wellbore after drilling considering hydration

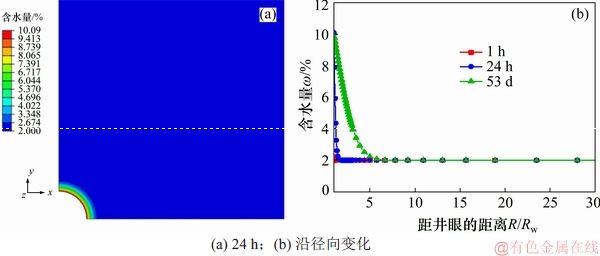
图12　地层钻开后井壁含水量分布

Fig. 12　Water content distribution of wellbore after drilling

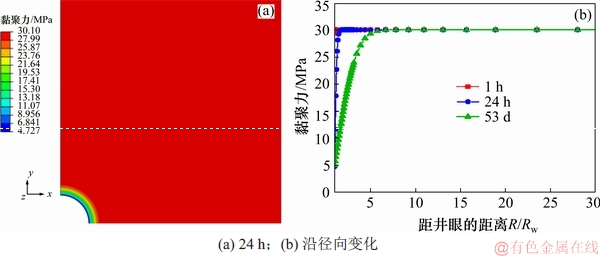
图13　不同距离下地层黏聚力的变化

Fig. 13　Variation of formation cohesion at different distances

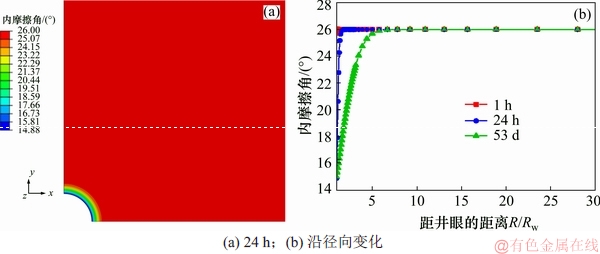
图14　不同距离下地层内摩擦角的变化

Fig. 14　Variation of internal friction angle of formation at different distances

图13和图14所示分别为钻井液当量密度为1.2时，地层岩石黏聚力和内摩擦角分布图。由于二者都受到含水量的控制以至于两者的分布规律与井壁围岩含水量的分布规律相类似，在地层钻开早期变化较为剧烈，此后变化减弱，然后逐渐地趋于一个定值。

钻井液当量密度为1.0和1.3时井眼渐进破坏过程分别如图15和16所示。可知：垂向(y方向)的破坏程度和范围明显比水平向(x方向)的大，破坏区基本呈椭圆形状，当钻井液当量密度为1.0时，浸泡1，7，14和24 d后的最大塑性应变分别为0.80%，1.03%，1.17%和1.30%，而当钻井液当量密度为1.3时，浸泡1，7，14和24 d后的最大塑性应变分别为0.50%，0.66%，0.73%和0.79%，可见，较小的钻井液当量密度加剧了井眼的水化破坏。就井眼破坏深度而言，由于水化效应的影响，在井眼浸泡早期，井眼破坏区域增加较为迅速，此后趋于稳定并逐渐呈线性增加趋势。

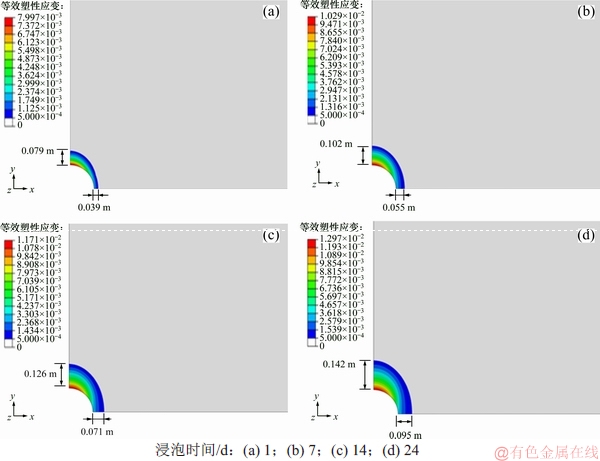
图15　钻井液当量密度为1.0时井眼渐进破坏过程

Fig. 15　Progressive failure process of wellbore with a drilling fluid equivalent density of 1.0

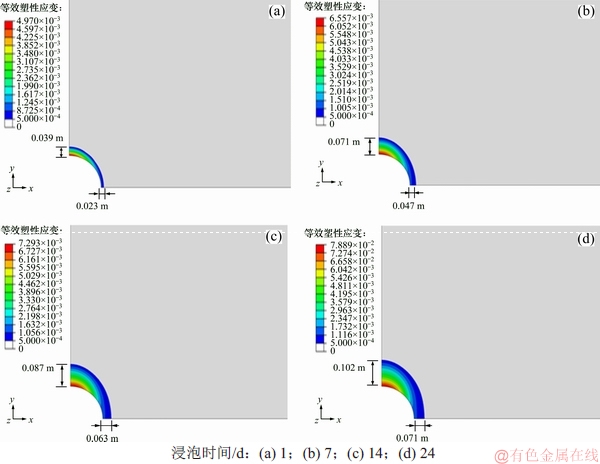
图16　钻井液当量密度为1.3时井眼渐进破坏过程

Fig. 16　Progressive failure process of wellbore with a drilling fluid equivalent density of 1.3

图17所示为不同钻井液当量密度下的井眼扩大率随时间变化曲线。从图17可以看出：随着浸泡时间增加井眼扩大率逐渐增大，不同钻井液当量密度下的井眼扩大率随着钻井液当量密度增大而减小。对比图9可知：以钻井液当量密度为1.2为例，在不考虑水化效应时，虽然有渗流场的影响，但其影响程度还不足以使得井眼扩大率随着时间发生改变，而考虑水化效应后，钻井后对应的扩眼率为18.07%，7 d后对应的扩眼率为58.22%，井眼扩大率增加约40%，可见水化效应对井眼渐进破坏的影响要远大于单纯渗流场的影响。

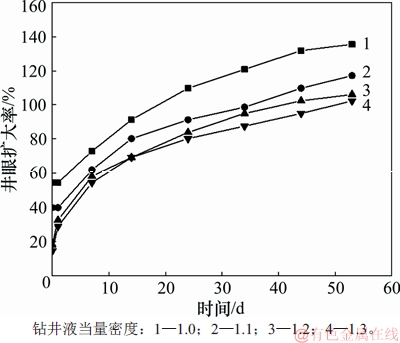
图17　考虑水化作用下的井眼扩大率随时间变化曲线

Fig. 17　Curve of wellbore enlargement rate with time under considering hydration

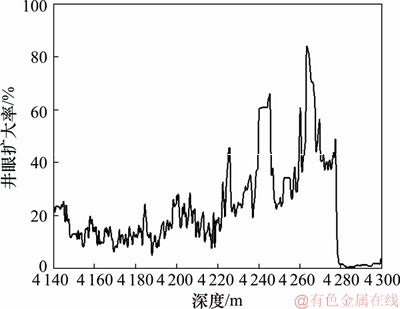
图18　W-82井径扩大率

Fig. 18　Diameter expansion rate of W-82 well

根据上述分析可知：在欠平衡钻井施工条件下，钻井扰动致使原有裂隙延伸变宽、新的微裂隙产生，微裂隙发生自吸水效应致使泥页岩水化膨胀，裂缝间联结强度降低，围岩整体强度逐渐降低，发生垮塌掉块现象，是导致井壁渐进失稳的内在因素。为此，在欠平衡钻井过程中，钻井速度要快，严格控制钻井液对泥页岩的抑制性能，并尽量减少循环时间，才能有效保证欠平衡钻井的顺利实施。

4.5　与现场结果对比

为了验证力-化耦合作用下井眼渐进破坏模型的可靠性与准确性，将数值模拟结果与现场实测资料进行了对比分析。

在实际的井眼钻开过程中，井眼扩大率只要控制在一定的范围之内，并且及时地冲洗干净井底岩屑，不造成井底岩屑的堆积，一般就不会引起卡钻的事故。工程上一般以平均井径扩大率不超过15%，产层段最大井径扩大率不超过30%且最大井径段占整个产层段比例不超过30%为合格。该井在四开井段采用密度不大于1.2 g/cm³的水基钻井液体系钻进沙河街组地层，钻进过程中井壁基本稳定，仅有几次轻微井塌，井下未发生复杂情况，井壁稳定条件满足欠平衡钻井施工要求，平均机械钻速为1.78 m/h，根据图17所示的计算结果，当井眼钻开后，井眼扩大率计算值约为18%，与现场结果相符。

在采用水基钻井液体系实施欠平衡钻井过程中，井筒和地层之间产生负压差，导致地层中的水向井筒中流动，从而减少了井漏的风险，并且降低了钻井液对地层的损害，但由于毛细管效应的存在会造成地层岩石发生自吸水化作用，特别是发育的微裂隙，造成泥页岩的吸水膨胀，水化效应更加显著，加上井眼缺乏了钻井液的压力平衡，加剧了井壁垮塌。中途起钻和测井工程中曾返出大量掉块，接立柱困难，短起下钻必须使用倒划眼才能进行，从井径曲线可以看到裸眼段存在多处大井眼井段(图18)，其中4 265~4 275 m段井眼扩大率在55%~85%之间，井眼扩大率计算结果约为84%。随后进行中途测试，至中途测试下钻通井泥浆浸泡地层长达53 d，掉块多(图19)，造成地层失稳，井壁大段坍塌，而本文预测的井眼扩大率已超过100%，垮塌严重，与实际钻井基本吻合，说明本文预测模型可以有效反映泥页岩井眼渐进动态破坏过程。

图19　W-82井返出掉块情况

Fig. 19　W-82 well returns block

4.6　讨论

W号构造沙河街组泥页岩破坏的内在原因是微孔洞、微裂隙的发育程度较高，主要包括3个方面：1) 原生裂缝较为发育；2) 钻井卸载作用使围岩产生新的裂缝；3) 硬脆性泥页岩毛细管效应较为显著，而毛细管效应产生的根本原因则是微裂缝的是否发育以及开度大小，次生裂缝伴随着毛细管自吸水化作用的发生而产生。过平衡钻井方式下钻井液密度较高，使得井筒内的压力高于地层压力，产生井筒与地层之间的正压差，促使原有的孔缝扩张和新的孔缝的产生，使得钻井流体侵入到地层内部产生水化作用；若采用欠平衡钻井方式，孔缝的存在会导致产生毛细管效应造成自吸水化作用促使泥页岩宏观破坏。无论是以哪种方式侵入地层，产生的水化作用将会促使原有的裂缝扩张和新的裂缝产生，进一步加剧了水化作用。可见，泥页岩微裂隙发育和逐步扩展是井壁渐进失稳的重要原因。

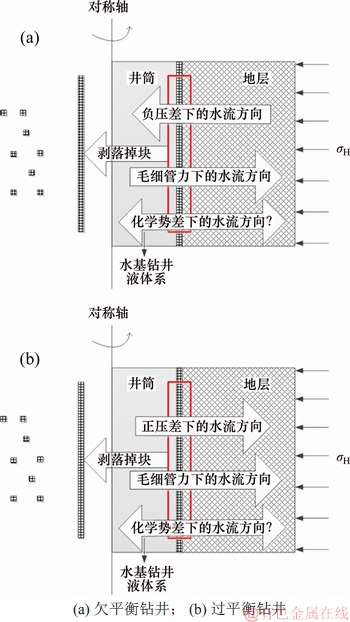
图20　钻井过程中水相流动示意图

Fig. 20　Schematic diagram of water phase flow during drilling

在欠平衡钻井方式下(图20(a))，地层的流体有控制地进入井筒，由于泥页岩的亲水特性致使钻井流体侵入地层产生倒吸现象，造成水化作用。化学势差作用下的水流方向取决于钻井液活度的影响，当钻井液活度较大时，化学势差作用下的水流方向指向地层，当钻井液活度较小时，水流方向则指向井筒。化学势差和负压差的综合效应是否能抵制毛细管力下的水流方向，主要取决于钻井液的活度和密度，但过低的钻井液密度会导致地层的支撑压力减小，从而增大了井眼围岩扰动区，加大了裂缝的扩展，也会加剧自吸现象。针对这种问题，有效的解决方法是提高钻井液的抑制能力，控制钻井液的活度，降低自吸水效应。

过平衡钻井方式下(图20(b))，井筒压力大于地层压力，正压差驱动井筒中的流体向地层侵入，使得钻井流体更多地进入地层，加剧了泥页岩的水化作用，弱化了围岩强度。同欠平衡钻井方式一样，化学势差作用下的水流方向取决于钻井液活度的影响，但其影响的程度不足以抵抗正压差和毛细管力的共同作用，总的水流方向指向地层，从而造成泥页岩的水化作用。总体而言，过平衡钻井方式下的井眼扰动程度较欠平衡钻井方式弱，但过平衡钻井方式下的水化作用比欠平衡钻井方式的强。针对这种问题，有效的解决方法是在提高钻井液抑制性的同时优选出有效的封堵材料加入钻井液中以强化钻井液的封堵性。

水化作用是影响井壁坍塌的重要因素，无论是欠平衡钻井方式还是过平衡钻井方式，都会产生水化作用，过平衡钻井方式较欠平衡钻井方式下水化更剧烈，更加不利于井壁的稳定，而影响水化作用的根本原因是微裂缝的发育与扩展。综上，有效的解决对策为：1) 优选有效的抑制剂，加入钻井液中以抑制硬脆性泥页岩中的黏土矿物；2) 优选有效的封堵材料，加入钻井液中以封堵微裂缝、微孔洞，降低钻井液侵入地层的能力；3) 优选润湿反转剂，加入钻井液中以改变岩石表面润湿性，防止毛细管自吸效应。

5 结论

1) 综合有效应力原理并结合吸水扩散和压力传递模型，建立了综合考虑化学势变化、流体流动与骨架变形耦合的泥页岩井眼渐进破坏分析模型，为了利用该模型模拟硬脆性泥页岩井眼动态破坏的整个过程，以ABAQUS软件为求解器，编制了计算程序，计算得到的结果与实际钻井基本吻合，验证了提出模型的有效性。

2) 考虑水化影响条件下，井眼扩大率随着钻井液浸泡时间的增大而增大，水化效应对井眼渐进破坏的影响要大于渗流场的影响。以钻井液当量密度1.2为例，不考虑水化效应时，随着时间的增加井眼并没有继续扩大，而考虑水化效应后， 7 d后的井眼扩大率增加约40%，水化起着非常重要的作用。

3) 中深层硬脆性泥页岩微裂隙较为发育，地层中伊/蒙混层矿物和伊利石含量较高，泥页岩易自吸水水化膨胀，为钻井过程中易发生井壁失稳的根本原因，在欠平衡钻井初期井眼并未出现失稳问题，随着浸泡时间的增加，井壁逐渐失稳。因此，在硬脆性泥页岩地层中实施钻井技术，仅仅依赖于提高钻井液密度来维护井壁稳定的方法不太可取，有效的解决方法则是强化钻井液的封堵性以及提高钻井液的抑制能力。

参考文献：

[1] 王荐, 卢淑芹, 朱宽亮, 等. 南堡油田保持中深层泥页岩井壁稳定钻井液研究[J]. 海洋石油, 2012, 32(1): 92-96.

WANG Jian, LU Shuqin, ZHU Kuanliang, et al. Maintaining wellbore stability in deep shale drilling in Nanpu oilfield[J]. Offshore Oil, 2012, 32(1): 92-96.

[2] 石秉忠, 夏柏如, 林永学, 等. 硬脆性泥页岩水化裂缝发展的CT成像与机理[J]. 石油学报, 2012, 33(1): 137-142.

SHI Bingzhong, XIA Bairu, LIN Yongxue, et al. CT imaging and mechanism analysis of crack development by hydration in hard-brittle shale formations[J]. Acta Petrolei Sinica, 2012, 33(1): 137-142.

[3] 赵亚宁, 陈金霞, 卢淑芹, 等. 南堡中深层复杂岩性地层井壁失稳机理及技术对策[J]. 钻井液与完井液, 2015, 32(5): 41-45.

ZHAO Yaning, CHEN Jinxia, LU Shuqin, et al. Instability mechanism and technical countermeasures for borehole wall in deep and complex lithologic strata in Nanpu[J]. Drilling Fluid & Completion Fluid, 2015, 32(5): 41-45.

[4] YEW C H, CHENEVERT M E, WANG C L, et al. Wellbore stress distribution produced by moisture adsorption[J]. SPE Drilling Engineering, 1990, 5(4): 311-316.

[5] 张乐文, 邱道宏, 程远方. 井壁稳定的力化耦合模型研究[J]. 山东大学学报(工学版), 2009, 39(3): 111-114.

ZHANG Lewen, QIU Daohong, CHENG Yuanfang. Research on the wellbore stability model coupled mechanics and chemistry[J]. Journal of Shandong University (Engineering Science), 2009, 39(3): 111-114.

[6] 邓金根, 郭东旭, 周建良, 等. 泥页岩井壁应力的力学-化学耦合计算模式及数值求解方法[J]. 岩石力学与工程学报, 2003, 22(S1): 2250-2253.

DENG Jingen, GUO Dongxu, ZHOU Jianliang, et al. Mechanics-chemistry coupling calculation model of borehole stressing shale formation and its numerical solution method[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(S1): 2250-2253.

[7] HEIDUG W K, WONG S W. Hydration swelling of water-absorbing rocks：a constitutive model[J]. International Journal for Numerical Analytical Methods in Geomechanics, 1996, 20(6): 403-430.

[8] LOMBA F T, CHENEVERT M E, SHAMA M M. The ion-selective membrane behavior of native shale[J]. Journal of Petroleum Science and Engineering, 2000, 25(1/2): 9-23.

[9] LOMBA F T, CHENEVERT M E, SHAMA M M. The role of osmotic effects in fluid flowthrough shale[J]. Journal of Petroleum Science and Engineering, 2000, 25(1/2): 25-35.

[10] CHEE P T, BRIAN G R. Managing physico-chemical wellbore instability in shales with the chemical potential mechanism[C]// SPE 36971, 1996.

[11] CHEE P T, BRIAN G R. Effects of swelling and hydration stress in shale on wellbore stability[C]// SPE 38057, 1997.

[12] CHEE P T, BRIAN G R. Integrated rock mechanics and drilling fluid design approach to manage shale instability[C]// SPE 47259, 1998.

[13] 王倩, 周英操, 唐玉林, 等. 泥页岩井壁稳定影响因素分析[J]. 岩石力学与工程学报, 2012, 31(1): 171-179.

WANG Qian, ZHOU Yingcao, TANG Yulin, et al. Analysis on effect factor in shale wellbore stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 171-179.

[14] 贾善坡, 张辉, 林建品, 等. 含水层储气库泥质岩盖层封气能力定量评价研究: 以里坦凹陷D5区二叠系含水层构造为例[J]. 水文地质工程地质, 2016, 43(3): 79-86.

JIA Shanpo, ZHANG Hui, LIN Jianpin, et al. Quantitative assessment of the gas-sealing capacity of the Permian claystone cap rock for the D5 aquifer gas storage in the Litan sag[J]. Hydrogeology & Engineering Geology, 2016, 43(3): 79-86.

[15] 周辉, 孟凡震, 张传庆, 等. 基于应力-应变曲线的岩石脆性特征定量评价方法[J]. 岩石力学与工程学报, 2014, 33(6): 1114-1122.

ZHOU Hui, MENG Fanzhen, ZHANG Chuanqing, et al. Quantitative evaluation of rock brittleness based on stress-strain curve[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1114-1122.

[16] RICKMAN R, MULLEN M, PETRE E, et al. A practical use of shale petrophysics for stimulation design optimization: all shale plays are not clones of the barnett shale[C]// SPE 115258, 2008.

[17] 卢运虎, 陈勉, 金衍, 等. 钻井液浸泡下深部泥岩强度特征试验研究[J]. 岩石力学与工程学报, 2012, 31(7): 1399-1405.

LU Yunhu, CHEN Mian, JIN Yan, et al. Experimental study of strength properties of deep mudstone under drilling fluid immersion[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1399-1405.

[18] 沈海超, 胡晓庆. 逆冲构造带精细地应力和井壁稳定性研究及应用. 新疆石油地质, 2011, 32(2): 193-196.

SHEN Haichao, HU Xiaoqing. Research on in-situ stress and wellbore stability of over thrust structural belt and its application[J]. Xinjiang Petroleum Geology, 2011, 32(2): 193-196.

[19] 程远方, 张锋, 王京印, 等. 泥页岩井壁坍塌周期分析[J].中国石油大学学报(自然科学版), 2007, 31(1): 63-66, 71.

CHENG Yuanfang, ZHANG Feng, WANG Jingyin, et al. Analysis of collapse period of mud shale shaft wall[J]. Journal of China University of Petroleum (Natural Science Edition), 2007, 31(1): 63-66, 71.

[20] YIN S, TOWLER B F, DUSSEAULT M B, et al. Fully coupled THMC modeling of wellbore stability with thermal and solute convection considered[J]. Transport in Porous Media, 2010, 84(3): 773-798.

[21] 黄浩勇. 泥页岩地层井壁坍塌周期数值模拟研究及应用[D]. 青岛: 中国石油大学石油工程学院, 2016: 20-23.

HUANG Haoyong. Numerical simulation of time dependent wellbore instability in shale formation and application[D]. Qingdao: China University of Petroleum. School of Petroleum Engineering, 2016: 20-23.

[22] ISLAM M A, SKALLE P, FARUK O. Analytical and numerical study of consolidation effect on time delayed borehole stability during underbalanced drilling in shale[C]// SPE 127554, 2009.

[23] 贾善坡, 陈卫忠, 杨建平, 等. 基于修正Mohr-Coulomb准则的弹塑性本构模型及其数值实施[J]. 岩土力学, 2010, 31(7): 2051-2058.

JIA Shanpo, CHEN Weizhong, YANG Jianping, et al. An elastoplastic constitutive model based on modified Mohr-Coulomb criterion and its numerical implementation[J]. Rock and Soil Mechanics, 2010, 31(7): 2051-2058.

[24] 贾善坡, 邹臣颂, 王越之, 等. 基于热-流-固耦合模型的石油钻井施工过程数值分析[J]. 岩土力学，2012，33(s2)：321-328.

JIA Shanpo, ZOU Chensong, WANG Yuezhi, et al. Numerical analysis of construction process of petroleum drilling based on thermal-hydro-mechanical coupling[J]. Rock and Soil Mechanics, 2012, 33(s2): 321-328.

[25] 陈益峰, 周创兵, 童富果, 等. 多相流传输THM全耦合数值模型及程序验证[J]. 岩石力学与工程学报, 2009, 28(4): 649-665.

CHEN Yifeng, ZHOU Chuangbing, TONG Fuguo, et al. A numerical model for fully coupled THM processes with multiphase flow and code validation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 649-665.

（编辑 杨幼平）

收稿日期： 2019 -02 -22; 修回日期： 2019 -05 -13

基金项目(Foundation item)：国家科技重大专项(2016ZX05006)；国家自然科学基金资助项目(51879259) (Project(2016ZX05006) supported by the National Science and Technology Major Program; Project(51879259) supported by the National Natural Science Foundation of China)

通信作者：贾善坡，博士，教授，博士生导师，从事油气岩石力学研究；E-mail: jiashanporsm@163.com