文章编号：1004-0609(2012)06-1754-09

高速压制成形粉末流动过程的

格子Boltzmann方法数值模拟

李俏杰，郑洲顺，王  爽，刘建康

(中南大学 数学与统计学院，长沙 410083)

摘  要：根据高速压制工艺过程的特点，底部和侧面边界采用反弹与反射的混合格式，顶部通过改变分布函数构造能模拟动态压制过程的边界格式。利用粉体的初始密度和压制最大理想密度建立一个动态的松弛函数来代替格子Boltzmann方法的固定松弛时间。对圆柱体及单级台阶的圆柱体模具的高速压制成形过程进行二维数值模拟，直观显示压制过程中粉末的流动以及应力波的形成与传播过程。模拟结果表明：模具形状对应力波的波形有较大影响；压制完成后，圆柱体压坯最大密度差为12 mg/cm³，密度分布均匀且左右对称，压坯顶部和底部密度较中间部分密度稍大，与实验结果基本相似；圆柱体压坯中存在密度较低的横向窄带区域，揭示成形坯有可能形成分层或断裂。

关键词：高速压制；格子Boltzmann方法；松弛函数；应力波

中图分类号：TF12     　　     文献标志码：A

Numerical simulation of powder flow in high velocity compaction by lattice Boltzmann method

LI Qiao-jie, ZHENG Zhou-shun, WANG Shuang, LIU Jian-kang

(School of Mathematics and Statistics, Central South University, Changsha 410083, China)

Abstract: According to the characteristics of high velocity compaction process, the rebound and reflection mixed boundary condition was used on the bottom and sides of the mould. By changing distribution function, a kind of boundary condition which can simulate the dynamic process was proposed. A relaxation function was established according to the powder flow characteristic using initial and maximum density. Two-dimensional numerical simulations were given to cylinder mould and single step cylinder mould. The dynamic evolution process of powders and the stress wave transformation process were presented. The results indicate that the shape of the mould has a great influence on the wave pattern of stress. The density of green compact is uniformly and symmetrically distributed, and the greatest density difference is 12 mg/cm³. The top and bottom parts have slight higher density than the middle part. These results are consistent with the experimental results. A narrow low density band is found in the green compact which reveals that there may exist density stratification.

Key words: high velocity compaction; lattice Boltzmann method; relaxation function; stress wave

高速压制成形(High velocity compaction，HVC)是2001年瑞典Hoaganas AB公司在美国金属粉末联合会上提出的一项粉体近终成形的新技术。由于它是一项低成本、高效率制备高密度粉末冶金零件的新技   术，具有良好的性价比而备受关注^[1-4]。目前，国内外对这项技术进行大量的研究主要有两类观点：第一种是基于连续介质理论，宏观上把粉末作为流体整体进行研究；另一种是从微观入手，对单颗粒的运动进行研究。HAGGBLAD等^[5]从宏观上运用有限元方法对钛粉的高速压制进行了模拟。KUMAR等^[6]采用多粒子配置方法从微观上研究了高速压制过程中颗粒的变形情况。郑洲顺等^[7-8]分别用离散单元法和元胞自动机对高速压制过程进行了模拟。格子Boltzmann方法(LBM)是从元胞自动机发展过来的一种新的数值模拟方法，是一种介于宏观和微观之间的介观数值方法，不需要介质的连续性假设且具有边界处理简单、程序易于实施等特点，被用于多种复杂现象的机理研究^[9]。本文作者将可压缩格子Boltzmann模型用于高速压制致密化过程，以分析粉末高速压制过程中粉末颗粒的运动特性及密度分布，对高速压制致密化机理进行初步的探索。

1  HVC格子Boltzmann模型的建立

粉末高速压制成形工艺过程如图1所示。上模冲与粉末接触，液压驱动的冲锤高速撞击上模冲，在约0.02 s时间内对粉体进行高能锤击，使其致密化。当高能量的冲击力载入时将产生应力波，使粉末颗粒之间形成一定强度的结合，颗粒发生塑性变形甚至局部焊合，最终达到高度致密化^[10]。

与传统压制相比，高速压制技术制备的压坯密度更高且密度分布均匀，压坯上下底部密度差值≤    10 mg/cm^3[11]。高速压制由于其较高的冲击能量，对模具材料有特殊要求，目前使用较成熟的模具有圆柱、圆环及具有单级台阶的模具。对圆柱及单级台阶的圆柱模具，由于其轴对称性，可以将模腔纵切面上的粉末假设为二维流动对其进行数值模拟。

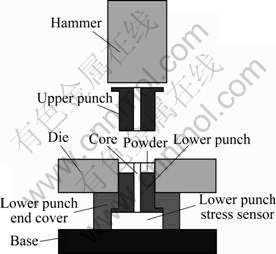
图1  HVC基本原理示意图

Fig. 1  Basic principle diagram of HVC

将模腔中粉末初始填充的区域视为一个二维阵列，用固定的网格将粉末所在的区域等分为M×N，粉末颗粒在网格上进行碰撞和流动。采用D2Q13多速度可压缩的格子Boltzmann模型^[12]，格子速度模型如图2所示。

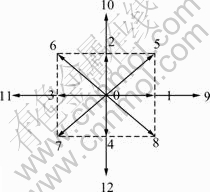
图2  D2Q13速度模型

Fig. 2  Velocity model of D2Q13

速度配置如下：

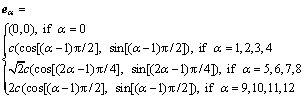     (1)

平衡态分布函数如下：

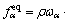
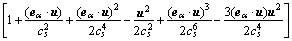  (2)

对应的权系数为

, , ,

, , , 。

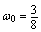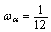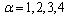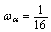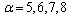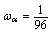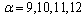式中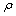：为密度；u为速度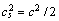；为格子声速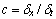；为格子速度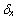；和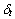分别表示空间和时间步长。

分布函数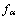演化方程采用单松弛时间的LBGK格式，即

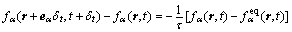    (3)

式中：r为格点位置；τ为松驰因子。

2  边界条件处理

2.1  侧面和底部边界条件处理

对于规则的几何形状，两侧面和底部边界可采用启发式边界处理格式，但由于在压制过程中顶部边界会随着粉末一起向下运动，需要特殊处理。为了提高边界精度和便于处理边界上粉末的碰撞和流动，假设在物理边界外存在一个虚拟的边界。在实际工艺过程中由于模壁涂有润滑剂，粉末与模壁既有摩擦作用又有润滑作用，所以边界格式采用反弹与镜面发射的混合格式^[9]应该更为准确，对底部边界处理方法如图3所示，其中A和B为流动区域内的格子层。

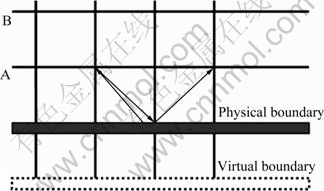
图3  底部边界条件处理

Fig. 3  Bottom boundary conditions processing

在反弹和镜面反射的混合边界条件下，物理边界上粉末颗粒不再发生碰撞。例如对模具底部边界，混合格式的边界可以表示为

            (4)

其中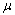：为弹回比例系数，表示粒子在与壁面作用时沿原路弹回所占的比例。在粉末压制过程中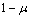，相当于摩擦因数。对侧面边界，只需改变对应的分布函数便可得到类似的计算公式。

2.2  顶部边界与应力传递分析

由于高速压制过程中，冲锤对上模冲产生一个瞬时的冲击，会对粉末体产生一个瞬时的外力，然后以应力波的形式在粉体中传播，使粉体致密。这个瞬时产生的冲击力和格子Boltzmann模型中的外力项^[13]不同，由于是瞬时的外力，其作用范围可能只在粉末的顶层，需要特殊处理。这个外力可看成是对顶部边界的作用，相当于压制过程。一般情况下可以假设应力波引起的分布函数的变化是在格子Boltzmann模型的碰撞阶段之前。因而，在原有3个阶段的基础上，再加入一个压制阶段，即压制→碰撞→流动→边界处理。压制过程可以看成邻近顶部边界的A层格位所包含的粉末粒子以“突变”的形式流动到B层和C层。如果我们假设一次碰撞流动过程粉末被压制一个格子，那么当粉末被压制一层格子之后，原来的第二层粉末变为第一层粉末格子(事实上是第一层粉末进入了第二层和第三层格子)，如图4所示。

以A层的r₁格点为例给出压制过程的具体处理步骤：

1) 对A层格位粒子执行碰撞过程

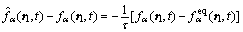       (5)

2) 执行流动过程

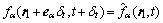                   (6)

3) 处理A层水平流动和静止的粉末，将其以突变形式流动至B层和C层，并将其速度方向改为斜指向粉末内部，即

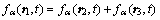                   (7)

图4  粉末压制过程示意图

Fig. 4  Schematic diagram of powder compaction process:  (a) Before compaction; (b) After compaction

4) 顶部边界下降一格，消除原A层格子(A层所有格位已经没有粉末)，完成压制过程。

                                (8)

式中：为碰撞后分布函数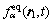；为平衡态分布函数。上述方案是一次压制的具体实现过程。事实上，对于一般情况，两次压制过程之间必然有多次的碰撞流动过程。可以考虑将粉末被压制一层格子的时间平均分配为N段，而每一阶段，进行一次碰撞流动过程。N的具体取值与上模冲的冲击能量有关。冲击能量越高，压制速度越快，N越小；冲击能量越低，压制速度越慢，N越大。N与冲击能量成反比例关系，具体关系式需由实验数据分析得出，需进一步研究。本文作者取N=50，相当于压制能量大约为6 kJ。

3  松弛时间的选取

压制致密化过程中，压制前期起主导作用的是冲锤产生的应力波，粉体流体性质明显，但在压制后期应力波效应减弱，随着粉体密度的增大其固体特性变得明显。导致这种现象出现的一个重要原因是粉体中后期的屈服效应^[14-15]明显，而流体一般没有这种效应，这也是粉体与流体的重要区别。屈服效应使粉体发生粘结导致能量损耗，使粉体流动性减弱。而流体中体现流动性的重要参数是运动黏度系数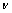，对应于LBE中的松弛参数τ。在LBGK模型中，一般采用固定的松弛参数，这对于一般流体而言是合理的，但是对粉体流动，τ应该是随时间和空间变化的。因此，对于粉体屈服效应建立粉体屈服原则，即找到松弛时间函数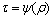，使得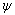必具备以下几个特征：

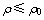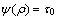1) 当时，，即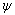为一常值函数，此时粉末表现为流体的特性；

2) 当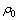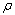＜≤时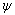，为单调递增函数，此时粉末以流体特性为主，随着密度的增大流动变得困难，表现出部分固体特性；

3) 当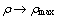时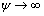，，压制后期密度接近最大值，粉末不再流动，粉末体现固体特性。

上述参数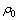、和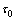都是可以调整的参数，对于不同的粉体有不同的值。例如，对于具体的松弛函数可以选取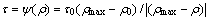，其与密度的关系如图5所示。

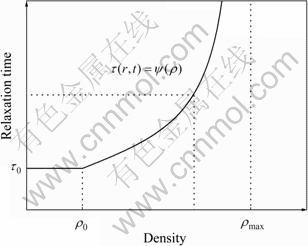
图5  松弛时间与密度的关系

Fig. 5  Relationship between relaxation time and density

4  模拟实现及分析

根据前面所建立的模型，高速压制成形的LBM程序流程图如图6所示。

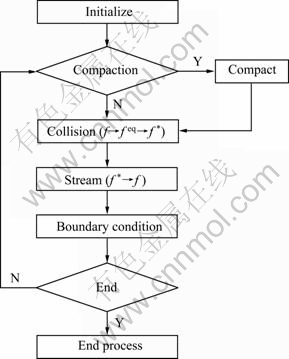
图6  高速压制LBM程序流程图

Fig. 6  Program flowchart of LBM in HVC simulation

流程图中数据的初始化包括参数和离散速度初始化、初始分布和宏观变量的计算、边界条件初始化等。

4.1  圆柱体模具的二维模拟

当粉末高速压制模具的模腔为圆柱体，其模腔纵切面上粉末的流动可假设为方形二维流动，其长和宽均为25 mm。以电解铜粉高速压制为例，其中L_x和L_y分别为模具的长和宽的网格数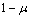，为摩擦因数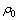，为松装密度，为压制最大理想密度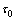，为初始松弛时间，具体参数如表1所列。

图7所示为二维等高方形HVC压制过程1 000时步内的密度场演化过程。从图中可以明显地看到在粉体的致密化过程中存在应力波的传播过程，且在压制初期只在模具顶部产生应力波，并逐渐向下传播。在模拟压制过程中，应力波在粉末中传递并不是以规则的波形向下传播，而是出现一定不规则形状。在step340时，应力波到达模具底部并反射回来继续对粉体进行致密；step600时，应力波到达顶部并与顶部产生的应力波相互叠加，进一步对粉体进行致密；step700时，压制过程停止，但应力波还继续在粉体中传播；step1000时，在应力波反复作用下，使粉体逐渐趋于均匀密度。

表1  电解铜粉高速压制模拟中的主要参数

Table 1  Main parameters of electrolytic copper powder simulation

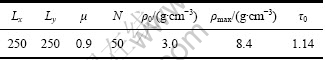
图7  圆柱体二维模拟密度场演化过程

Fig. 7  Density evolution of two-dimension cylinder mould: (a) Step 20; (b) Step 100; (c) Step 200; (d) Step 300; (e) Step 340; (f) Step 400; (g) Step 500; (h) Step 600; (i) Step 700; (j) Step 800; (k) Step 900; (l) Step 1 000

为方便统计和分析密度分布，将压制完成后每个网格上的密度绘出其密度曲面图，如图8所示。

由图8不难看出，其密度分布具有一定的规律：1) 压坯总体密度分布均匀，最大密度差为12 mg/cm³,顶部和底部密度稍大，中间部分密度稍小，在中间部分出现一个大约0.26 mm宽的低密度窄带，可能出现一个密度分层；2) 左右密度基本对称；3) 压制完成后，并没有达到最大理想密度，平均密度为7.948 g/cm³，为最大理想密度的94%左右。所得结果与图9所示的高速压制实验结果^[11]基本相符合。

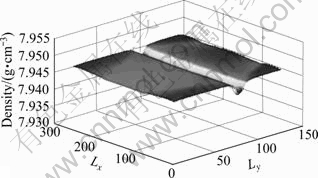
图8  压制完成后密度分布曲面图

Fig. 8  Simulation diagram of density distribution after compaction

图9  电解铜粉采用两种成形方法制备圆柱体的密度分布^[11]

Fig. 9  Density distribution of cylinder made of electrolytic copper powder using two processes^[11]

4.2  单级台阶的圆柱体二维模拟

具有单级台阶的圆柱体模具，其纵切面是一个“凸”形，由于其形状复杂，压制过程要比圆柱体的压制更为复杂，其纵切面示意图如图10所示。

图10  单级台阶的圆柱体纵切面示意图

Fig. 10  Sketch map of vertical section of cylinder mould with single steps

下面同样以电解铜粉高速压制为例，具体参数如表2所列。

表2  单级台阶圆柱体模拟中的主要参数

Table 2  Main parameters of simulation of single steps cylinder mould

图11所示为取上述参数时密度场的演化过程。从图11中可以看出，在单级台阶的圆柱体与不带台阶的圆柱体压制中，应力波的传递过程有较大的区别。在step300时，接近模具底部的粉体侧向流动较为明显；step500时，底部两侧粉体在上下应力波叠加作用下密度快速增大；step700时，底部反射回的应力波与顶部产生的应力波相互叠加，出现一个三角形的波形；step1000时，粉体密度基本均匀。

为考虑单级台阶圆柱体密度分布情况，对图10中的中轴线AB和CD的密度进行分析，得到如图12所示的密度分布曲线。

从图12中可以发现，AB线上的密度左右基本呈对称分布，两底部端角处密度较低，中间部分密度较高，CD线上顶部密度相对较高，接近底部，密度逐渐降低，与圆柱体模具顶部和底部密度较大不同，这应是其单级台阶模具形状造成的，在底部，应力波侧向传播，致密化程度稍低一些。同样压制完成后没有达到最高的理想密度，平均密度为7.84 g/cm³，只有最高理想密度的93%左右。

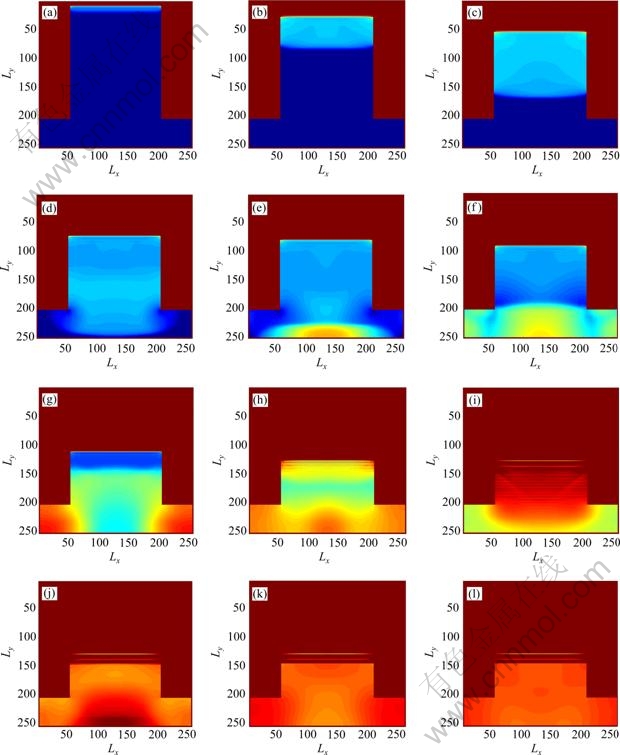
图11  单级台阶圆柱体二维模拟密度场演化过程

Fig. 11  Density evolution in two-dimension of single steps cylinder mould: (a) Step 20; (b) Step 100; (c) Step 200; (d) Step 300;  (e) Step 340; (f) Step 400; (g) Step 500; (h) Step 600; (i) Step 700; (j) Step 800; (k) Step 900; (l) Step 1 000

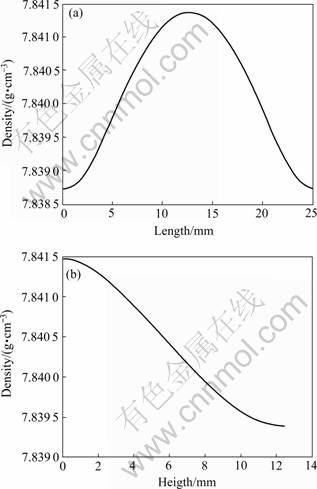
图12  压制完成后中轴线AB和CD上的密度分布

Fig. 12  Density distribution of middle lines AB(a) and CD(b) after compaction

5  结论

1) 针对高速压制过程特性，改变格子Boltzmann方法的边界条件使其能模拟压制过程；根据粉体特性建立松弛函数，实现高速压制过程的动态模拟，验证格子Boltzmann模型的有效性。

2) 对圆柱体和单级台阶的圆柱体模具，再现压制过程中应力波的传播与演化过程。不同模具形状应力波的形状有较大变化，其致密化程度也有所不同，圆柱体的致密化程度比带台阶的圆柱体致密化程度稍高，所以在模具设计时应避免复杂的形状。

3) 对圆柱体模具，压坯最大密度差为12 mg/cm³，密度分布总体均匀，但在中间部分出现一个密度较低的窄带，可能会出现一个分层。为减小密度差，可提高冲锤的冲击能量。

REFERENCES

[1] SKGLUND P. High density P/M components by high velocity compaction[C]//Proceedings of 2001 International Conference on Powder Transmission Components. Ypsilanti: MPIE, 2001: 16-17.

[2] ORBARL. New research directions in powder metallurgy[J]. Romanian Reports in Physics, 2004, 56(3): 505-516.

[3] RICHARD F. HVC punches PM to new mass production limits[J]. Metal Powder Report, 2002, 57(9): 26-30.

[4] 周晟宇, 尹海清, 曲选辉. 粉末冶金高速压制技术的研究进展[J]. 材料导报, 2007, 21(7): 79-81.
ZHOU Sheng-yu, YIN Hai-qing, QU Xuan-hui. Research status of high velocity compaction in powder metallurgy[J]. Materials Review, 2007, 21(7): 79-81.

[5] HAGGBLAD H A, HOCKAUF M, ERIKSSON M, BERGGREN C. Simulation of high velocity compaction of powder in a rubber mould with characterization of silicone rubber and titanium powder using a modified split Hopkinson set-up[J]. Powder Technology, 2005, 154: 33-42.

[6] KUMAR D R, KUMAR R K, PHILIP P K. Simulation of dynamic compaction of metal powders[J]. Journal of Applied Physics, 1999, 85(2): 767-775.

[7] 郑洲顺, 王 爽, 郑 珊, 曲选辉. 基于离散单元法的粉末高速压制流动过程的模拟[J]. 稀有金属材料与工程, 2010, 39(12): 2132-2136.
ZHENG Zhou-shun, WANG Shuang, ZHENG Shan, QU Xuan-hui. Numerical simulation of particle flow for high velocity compaction based on discrete element method[J]. Rare Metal Materials and Engineering, 2010, 39(12): 2132-2136.

[8] 郑洲顺, 于万春子, 诸葛金平, 梁 登. 粉末高速压制成形二维流动的元胞自动机模拟[J]. 系统仿真学报, 2009, 21(21): 6825-6828.
ZHENG Zhou-shun, YUWAN Chun-zhi, ZHUGE Jin-ping, LIANG Deng. CA numerical simulation for two-dimensional flow of HVC[J]. Journal of System Simulation, 2009, 21(21): 6825-6828.

[9] 何雅玲, 王 勇, 李 庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009.
HE Ya-ling, WANG Yong, LI Qing. Lattice Boltzmann method: Theory and applications[M]. Beijing: Science Press, 2009.

[10] 沈元勋, 肖志瑜, 温利平, 潘国如, 李元元. 粉末冶金高速压制技术的原理、特点及其研究进展[J]. 粉末冶金工业, 2006, 16(3): 19-21.
SHEN Yuan-xun, XIAO Zhi-yu, WEN Li-ping, PAN Guo-ru, LI Yuan-yuan. Principle, characteristics and status of high velocity compaction technology in powder metallurgy[J]. Powder Metallurgy Industry, 2006, 16(13): 19-21.

[11] 王建忠. 铁粉和铜粉高速压制成形及致密化规律研究[D]. 北京: 北京科技大学, 2009: 1-161.
WANG Jian-zhong. Study on densifying law and high velocity compaction of iron and copper powders[D]. Beijing: Beijing University of Science and Technology, 2009: 1-161.

[12] TANG Gui-hua, GU Xiao-jun, BARBER R, EMERSON D, ZHANG Yong-hao. Lattice Boltzmann simulation of nonequilibrium effects in oscillatory gas flow[J]. Physical Review E, 2008, 78(2): 026706-026714.

[13] GUO Zhao-li, ZHENG Chu-guang, SHI Bao-chang. Discrete lattice effects on the forcing term in the lattice Boltzmann method[J]. Physical Review E, 2002, 65(4): 046308 1-6.

[14] 果世驹, 迟 悦, 孟 飞, 杨 霞. 粉末冶金高速压制成形的压制方程[J]. 粉末冶金材料科学与工程, 2006, 11(1): 24-27.
GUO Shi-ju, CHI Yue, MENG Fei, YANG Xia. Compaction equation for high velocity compact shaping of powder metallurgy[J]. Materials Science and Engineering of Powder Metallurgy, 2006, 11(1): 24-27.

[15] 郑洲顺, 徐勤武, 朱远鹏, 曲选辉. 金属粉体高速压制成形过程的应力—应变曲线特征分析[J]. 中国有色金属学报, 2011, 21(4): 888-893.
ZHENG Zhou-shun, XU Qin-wu, ZHU Yuan-peng, QU Xuan-hui. Characteristics analysis of stress—strain curves of metal powders during high velocity compaction process[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(4): 888-893.

(编辑 李艳红)

基金项目：国家自然科学基金资助项目(50874123，51174236)；国家重点基础研究发展计划资助项目(2011CB606306)

收稿日期：2011-08-30；修订日期：2012-01-28

通信作者：郑洲顺，教授，博士；电话：0731-88660172；E-mail: 2009zhengzhoushun@163.com