
Mathematical model of electromagnetic elimination in tubule with high frequency magnetic field
GUO Qing-tao(郭庆涛), JIN Jun-ze(金俊泽), LI Ting-ju(李廷举),
WANG Tong-min((王同敏), ZHANG Qi(张 琦), CAO Zhi-qiang((曹志强)
State Key Laboratory of Materials Modification by Laser, Ion and Electron Beams,
School of Materials Science and Engineering, Dalian University of Technology, Dalian 116024, China
Received 10 April 2006; accepted 25 April 2006
Abstract: In order to find the ways to improve the elimination efficiency with high frequency magnetic field, a mathematical model of electromagnetic elimination (EME) in the tubule with high frequency magnetic field was set up. The calculated results show that by ignoring the flow of molten metal, when the surface magnetic induction intensity of the metal (B0) is 0.03 T and the diameter of the tubule is 8 mm, the non-metallic inclusions with 30 μm diameter can be wiped off in 7 s from the center of the molten aluminum, whereas the elimination time of the 5 μm non-metallic inclusions is more than 240 s. When B0 is 0.03 T, the diameter of the tubule is 8 mm and elimination time is more than 30 s, the elimination efficiency of 5μm, 10 μm and 30 μm non-metallic inclusions is about 60%, 90% and 100%, respectively, the elimination efficiency increases with the decreasing diameter of the tubule. It can be concluded that increasing the magnetic induction intensity or decreasing the diameter of the tubule can decrease the elimination time and improve the elimination efficiency in EME with high frequency magnetic field.
Key words: electromagnetic elimination, non-metallic inclusions, elimination time, elimination efficiency
1 Introduction
Electromagnetic elimination(EME) is a well- established industrial method. A wide variety of specific technical application exists, ranging from separation of uranium isotope in the early nuclear era to separation of aluminum cans and other nonferrous metals from household or industrial waste [1]. In recent years, the methods of EME have been proposed and tested in purifying the molten metals, such as induction coil elimination [2-4], traveling magnetic field elimination [5-7] and high magnetic field elimination [8], etc. Because of its convenience, the method of high frequency field elimination has become one of the main research focuses. SHOJI et al [9] have calculated the electromagnetic force in liquid steel flowing in the circular pipe. However, the model can only calculate the force in about 1.5 δ(δ is the skin depth ).
In this paper, a mathematical model of EME in the tubule with high frequency magnetic field was set up. The electromagnetic body force (EMF) that distributes throughout the metal, elimination velocity and elimination time were deduced respectively. The relationships between EMF and B0, EMF and 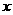 (the distance from the metal surface), elimination time and the diameter of the non-metallic inclusions, elimination efficiency and the diameter of the tubule were also analyzed.
(the distance from the metal surface), elimination time and the diameter of the non-metallic inclusions, elimination efficiency and the diameter of the tubule were also analyzed.
2 Theory calculation of mathematical model of EME
2.1 Principle
The electromagnetic body force can be generated by the interaction between alternating magnetic field and induced current in the molten metal. Because of the different electric resistance between the metal and the non-metallic inclusions, non-metallic inclusions will migrate opposite to the EMF and then can be wiped off. This is the theory of EME. Fig.1 shows the schematic diagram of EME with high frequency magnetic field.
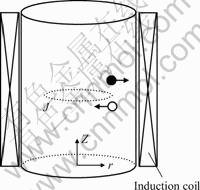
Fig.1 Principle of electromagnetic purification with high frequency magnetic field: ● Non-metallic inclusions;
○ Metal
EMF points to the inner of the molten metal in the direction of  .
.
2.2 Electromagnetic body force
The EMF perpendicular to the surface of strand and pointing to the inner of conductor is described as [10]:
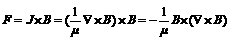 (1)
(1)
where 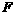 is EMF in radial, N/m3;
is EMF in radial, N/m3; 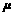 is the magnetic permeability, H/m and
is the magnetic permeability, H/m and 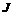 is the electric current density, A/m2. For electromagnetic solenoid,
is the electric current density, A/m2. For electromagnetic solenoid, 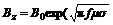 ),
),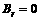 and
and 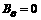 are taken into account, so following equation can be obtained,
are taken into account, so following equation can be obtained,
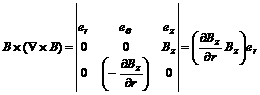 (2)
(2)
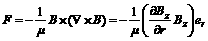 (3)
(3)
Then Eqn.(4) can be obtained,
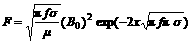 (4)
(4)
where 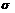 is the electrical conductivity of molten metal and f is the frequency of the electrical source.
is the electrical conductivity of molten metal and f is the frequency of the electrical source.
2.3 Electromagnetic pinch force
Based on the theory of LEENOV et al [11], electromagnetic pinch force can be calculated with the following equation:
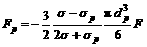 (5)
(5)
where 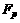 is the electromagnetic pinch force;
is the electromagnetic pinch force; 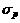 is electrical conductivity of the non-metallic inclusion and
is electrical conductivity of the non-metallic inclusion and 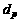 is the diameter of the non-metallic inclusion. Comparing to
is the diameter of the non-metallic inclusion. Comparing to 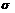 ,
, 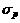 is so little that it can be omitted, Eqn.(6) can be obtained as follows,
is so little that it can be omitted, Eqn.(6) can be obtained as follows,
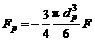 (6)
(6)
It can be seen that the electromagnetic pinch force is in the opposite direction of EMF.
2.4 Viscosity resistance
Viscosity resistance can be calculated with Eqn.(7) [12],
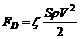 (7)
(7)
where 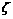 is the damping coefficient;
is the damping coefficient; 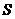 is the area of the inclusions;
is the area of the inclusions; 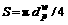 ;
; 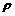 is the density of the inclusions;
is the density of the inclusions; 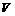 is the relative velocity.
is the relative velocity.
On the assumption that the flow of the molten metal is laminar flow, the inclusion Reynolds number is defined as:
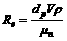 (8)
(8)
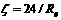 (9)
(9)
where 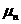 is viscosity of molten metal. Then
is viscosity of molten metal. Then 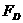 can be described as
can be described as
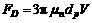 (10)
(10)
2.5 Elimination velocity
When viscosity resistance equals to electromagnetic pinch force, the maximal velocity ( ) of the inclusions in molten metal can be obtained:
) of the inclusions in molten metal can be obtained:
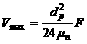 (11)
(11)
Substituting Eqn.(4) into Eqn.(11) and Eqn.(12) can be obtained as
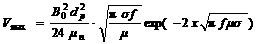 (12)
(12)
2.6 Elimination time
Fig.2 shows the schematic diagram of the movement of the non-metallic inclusion in the molten metal. EMF parallels to the direction of X and the flow of the molten metal is in the direction of Z.
When the inclusion begin to move, V0 approximates to zero so that FD can be ignored, then the acceleration of
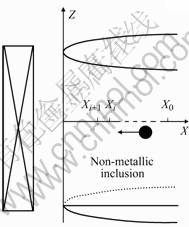
Fig.2 Schematic diagram of movement of non-metallic inclusion in molten metal
the inclusion can be described as
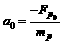 (13)
(13)
The locomotive time of the inclusion from X0 to X1 is:
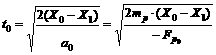 (14)
(14)
If 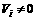 , then
, then
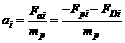 (15)
(15)
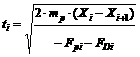 (16)
(16)
In the calculation, we can’t get reasonable results in case of too large Vi it will lead to 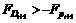 . Then Vi must be calculated once more, as follows:
. Then Vi must be calculated once more, as follows:
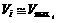 (17)
(17)
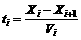 (18)
(18)
The total time is:
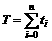 (19)
(19)
3 Calculation results and discussion
Calculation parameters are listed in Table 1.
Fig.3 shows that EMF increases with the increase of B0 and decreases with the increase of the distance from
Table 1 Calculation parameters
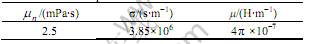
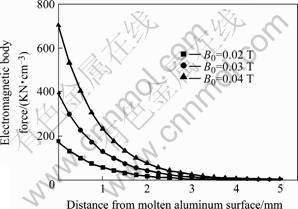
Fig.3 Effects of B0 on distribution of EMF in molten aluminum when f=20 kHz
the molten aluminum surface when f is 20 kHz. Fig.4 shows the distribution of EMF in the molten metal with the varying of frequency when B0=0.03 T. EMF of the metal surface is increased with the increase of the frequency while the skin depth is decreased.
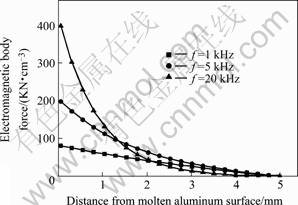
Fig.4 Effects of frequency on distribution of EMF in molten aluminum when B0=0.03 T
Because EMF increases with the increase of B0, higher elimination efficiency can be got if B0 is increased. However with the increase of B0, J is increased, and then the temperature of the molten metal is increased with it. So B0 can’t be increased too much in order to keep the temperature of the metal.
Fig.5 shows the elimination time in molten aluminum with high frequency magnetic field when diameter of the tubule is 8 mm.It can be seen from Fig.5 that elimination time of the inclusions increases with the increase of the distance from the melt surface and decreases with the increase of the diameter of the inclusions. The elimination time of the inclusions with 5 μm diameters near the center of the sample is more than 250 s, but 30 μm inclusions can be eliminated in 7 s when B0 is 0.03 T and f is 20 kHz.
Fig.6 shows the elimination efficiency of the various dimension inclusions with high frequency magnetic field. The elimination efficiency increases with the increase of the diameter of the inclusions and the elimination time. When B0 is 0.03 T, the diameter of the tubule is 8 mm and elimination time is more than 30 s, the elimination efficiency of 5 μm, 10 μm and 30 μm non-metallic inclusions is about 60%, 90% and 100%, respectively.
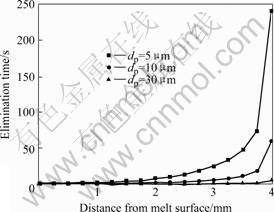
Fig.5 Relationship between elimination time and position of various dimension inclusions in liquid aluminum

Fig.6 Relationship between elimination efficiency and time of various dimension inclusions in aluminum melt(B0=0.03 T)
Fig.7 shows the relationship between elimination efficiency and the diameter of the tubule. It can be seen that elimination efficiency increases with the decrease of the diameter of the tubule. Elimination efficiency is about 100% with 10 μm non-metallic inclusions when the diameter of the tubule is 6 mm and elimination time is 20 s, while it decreases to 65% when the diameter of
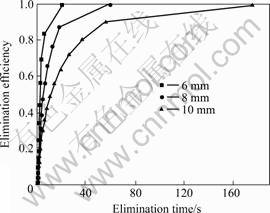
Fig.7 Elimination efficiency in various diameter tubule with high frequency magnetic field when B0=0.03 T and dp=10 μm
the tubule is 10 mm.
TAKASHI et al [13,14] have discussed the effects of the turbulence in the EME. Thin tubule can restrain the turbulence and increase elimination efficiency in EME. With the decrease of the diameter of the tubule, the flux through the tubule can be decreased as well. Therefore a bundle of tubules should be applied in order to increase the flux in the EME.
4 Conclusions
1) Electromagnetic body force increases with the increase of the magnetic induction intensity; the force density of the molten metal surface is increased with the increase of the frequency while the skin depth is decreased.
2) The non-metallic inclusions with the diameter 30 μm can be wiped off in 7 s from the center of the molten aluminum while the elimination time of the 5 μm non-metallic inclusions is more than 240 s when B0 is 0.03 T and the diameter of the tubule is 8 mm.
3) When B0 is 0.03 T, the diameter of the tubule is 8 mm and elimination time is more than 30 s, the elimination efficiency of 5, 10 and 30 μm non-metallic inclusions is about 60%, 90% and 100%, respectively.
References
[1] SERGEY M, REINHOLD L, DIRAN A. Electromagnetic separation techniques in metal casting(Ⅰ). Conventional methods[J]. IEEE Transactions on Magnetics. 2000, 36(4): 2015-2021.
[2] SASSA K, YAMAO H, ASAI S. Separation of inclusions in liquid metal using fixed alternating magnetic field [A]. International symposium on electromagnetic processing of materials [C]. Paris, 1997. 157-161.
[3] KOICHI TAKAHASHI, SHOJI TANIGUCHI. Electromagnetic separation of nonmetallic inclusion from liquid metal by high frequency magnetic field [J]. ISIJ International, 2003, 43(6): 820-827.
[4] LI Ke, SUN Bao-de, LI Tian-xiao, et al. Application of high frequency magnetic field to separate inclusion particles in aluminum melt [J]. Acta Metallurgica Sinica, 2001, 37(4): 405-410.
[5] SHU Da, SUN Bao-de, LI Ke, et al. Continuous separation of non-metallic inclusions from aluminum melt using alternating magnetic field [J]. Materials Letters, 2002, 55: 322-326.
[6] ZHONG Yun-bo, REN Zhong-ming, DENG Kang, et al. Continuously purifying experiment of aluminum base alloy melt by traveling magnetic field [J]. The Chinese Journal of Nonferrous Metals, 2001, 11(2): 167-171.
[7] TANAKA Y, SASSA K, IWAI K, et al. Separation of nonmetallic inclusions from molten metal using traveling magnetic field [J]. Tetsu-to-Hagane, 1995, 81(12): 12-17
[8] NORIHISA W, KENSUKE S, SHIGEO A. Magnetic separation of inclusion in molten metal using a high magnetic field [J]. Tetsu-to-Hagane, 2000, 86(6): 363-369.
[9] SHOJI T, J.KEITH B. Theoretical study on the separation of inclusion particles by pinch force from liquid steel flowing in a circular pipe[J]. Tetsu-to-Hagane, 1994, 80(1): 24-29.
[10] NA Xian-zhao, ZHANG Xing-zhong, GAN Yong. Mathematical analysis and numerical simulation of high frequency electromagnetic field in soft contact continuous casting mold[J]. ISIJ International, 2002, 42(9): 974-981.
[11] LEENOV D, KOLIN A. Theory of Electromagnetophoresis. I. Magnetohydrodynamic Forces Experienced by Spherical and Symmetrically Oriented Cylindrical Particles[J]. Journal of Chemical Physics, 1954, 22(4): 683-688.
[12] DOUGLAS J F, GASIOREK J M, SWAFFIELD J A. Fluid Mechanics [M]. Beijing: Higher Education Press, 1992. (in Chinese)
[13] TAKASHI S, NAGY E. Kinetics of inclusion removal in electromagnetically driven recirculating flows[A]. International symposium on electromagnetic processing of materials[C]. Nagoya ISIJ, 1994.
[14] KOICHI T, SHOJI T. Electromagnetic separation of nonmetallic inclusion from liquid metal by imposition of high frequency magnetic field[J]. ISIJ International, 2003, 43(6): 820-827.
(Edited by ZHAO Jun)
Foundation item: Projects (50474055; 50274018) supported by the National Natural Science Foundation of China; project (20052176) supported by the Natural Science Foundation of Liaoning, China
Corresponding author: GUO Qing-tao; Tel: +86-13604259195; E-mail: mystone_2002@tom.com