Trans. Nonferrous Met. Soc. China 23(2013) 1459-1464

Rigorous back analysis of shear strength parameters of landslide slip

Ke ZHANG¹, Ping CAO¹, Rui BAO^1,2

1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Kunming Prospecting Design Institute of China Nonferrous Metals Industry, Kunming 650000, China

Received 25 April 2012; accepted 21 September 2012

Abstract: A rigorous back analysis of shear strength parameters of landslide slip was presented. Kinematical element method was adopted to determine factor of safety and critical failure surface, which overcomes the disadvantage of limit equilibrium method. The theoretical relationship between the combination of shear strength parameters and stability state was studied. The results show that the location of critical slip surface, F/tan  and F/c depend only on the value of c/tan . The failure surface moves towards the inside of slope as c/tan  increases. According to the information involving factor of safety and critical failure surface in a specific cross-section, strength parameters can be back calculated based on the above findings. Three examples were given for demonstrating the validity of the present method. The shear strength parameters obtained by back analysis are almost consistent with their correct solutions or test results.

Key words: slope stability; back analysis; kinematical element method; shear strength parameter; critical failure surface

1 Introduction

The determination of shear strength for landslide slip is an important research object in slope stability analysis. It is widely accepted that the shear strength parameters obtained by back analysis are more reliable than those by laboratory or in-situ test. However, back analysis is a much more difficult task. Many studies have indicated that it is insufficient to assess shear strength parameters from the information provided by a failure surface. This can be done in two ways [1-3]: one is by assuming one of these parameters; the other is by establishing a set of simultaneous equations involving the information of two cross-sections. The back analysis can also be treated as the optimization problem. Nguyen [4] developed a simple and quick method for the back calculation of slope failures by the secant method. LI et al [5] presented hybrid genetic algorithm, and used the optimization algorithm to identify the shear strength parameters of geotechnical materials. JIANG and YAMAGAMI [6,7] illustrated the theoretical relationship between the strength parameters and the critical slip surface, and produced a new method for back analysis of strength parameters.

One of the key problems of back analysis is to calculate the factor of safety. The limit equilibrium method was adopted in the aforementioned researches, and they assumed that the slip surface is a circular one. Since this method is a statically indeterminate problem, assumptions on the inter-slice shear forces are employed to render the problem statically determinate. It is difficult to assess the accuracy of the limit equilibrium solution.

Kinematical element method (KEM) is an advanced slope limit analysis technology presented by Gussmann [8] with strong theoretical background. Cao and GUSSMANN [9] improved this method, and developed KEM analysis software. Gussmann [10] solved the limit-load problem by the KEM. Li et al [11] used KEM to analyze bottom stability of foundation pit. The main advantages of KEM are as follows: 1) it avoids assumptions of inter-slice forces in limit equilibrium method; 2) no assumption needs to be made on geometry of the slip surface; and 3) the inter-element boundaries do not have to be vertical.

The internal relationship between the combination of shear strength parameters and stability state was studied. Based on the above-mentioned relationship, a rigorous back analysis combining KEM was presented, which provided a practical and rigorous way to determine shear strength parameters of landslide slip. According to the information involving the factor of safety and the critical slip surface in a specific cross- section, strength parameters can be back calculated.

2 Theoretical background of KEM

The theory of KEM includes three parts: kinematics analysis, static analysis and optimization. First, plastic sliding zone is divided into several block elements called kinematical elements (Fig. 1). The normal force and shear force acting on the internal boundary satisfy Mohr– Coulomb failure criterion.

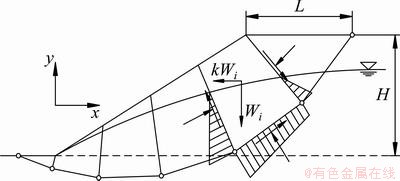
Fig. 1 Slope stability analysis model of KEM

Taking the compatibility condition of movement for elements, kinematics equation is given as

                               (1)

where K represents kinematics coefficient matrix, V represents the vector of unknown displacements of elements, and  represents the known displacements vector on flexible boundary.

After solving the above equations, the directions of relative movement of elements are obtained. The horizontal and vertical force equilibriums for each element are converted into the matrix form, and effective normal force applied on the element is taken as unknown quantity,

                              (2)

where K_s represents the static coefficient matrix, N represents the vector of unknown effective norm stress on the element, and F represents the vector of known force.

The factor of safety is obtained by employing iteration process after solving the static equations. Factor of safety is taken as an objective function, and the coordinates of the points defining the failure surface are taken as the control variables. Optimization algorithm is used to search the minimum factor of safety and critical slip surface.

3 New back analysis

3.1 Theoretical background

In slope stability analysis, the factor of safety F is usually defined as the ratio of the shear strength of the soil to the shear stress necessary to bring the slope into a state of limit equilibrium [12]. The strength of the soil is usually described by Mohr–Coulomb criterion as a function of the cohesion c and friction angle 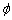. F can be given by

                            (3)

where  and  are the strength parameters necessary only to maintain the slope in limit equilibrium.

In order to demonstrate the internal relationship between the combination of strength parameters and stability state, one may consider a homogeneous slope with shear strength parameters c and 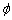. The location of critical slip surface and factor of safety F can be uniquely determined, and  is obtained from Eq. (3). Let another slope be comprised of soil with shear parameters  and   and other parameters remain constant. The location of critical slip surface and factor of safety F' can also be determined. Let , which means that the parameters are all the same under limit equilibrium state. At the moment   and . Based on the definition of factor of safety, F'=wF is obtained. The relationship is given by

                         (4)

Many researchers have developed stability charts of simple homogeneous slopes by the relationship described above [6,12,13].

To demonstrate the theoretical relationship between  and stability state (F/tan , F/c and location of critical slip surface), the multi-step slope from Ref. [14] was selected as the analysis example. The soil parameter values are listed as follows: unit weight γ=18 kN/m³, cohesion c=60 kPa, and friction angle 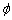=18°. The factor of safety and critical failure surface are obtained by KEM.

Five different combinations of strength parameters (c and ) with the same value of c/tan  were considered. The results are shown in Table 1 and Fig. 2. The location of critical slip surface and the values of F/tan  and F/c remain the same for the constant value of c/tan .

Table 1 F/tan   and F/c with same value of c/tan

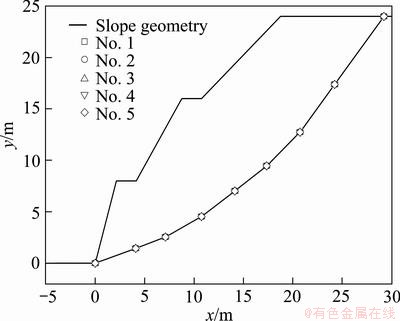
Fig. 2 Location of critical slip surfaces with same value of c/tan

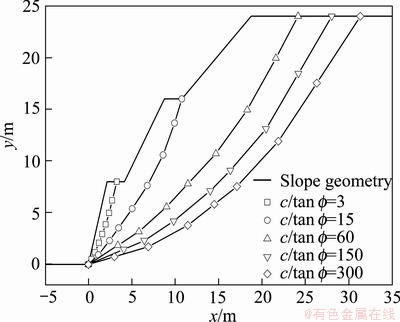
Fig. 3 Location of critical slip surfaces with different values of c/tan

Table 2 F/tan  and F/c with different values of c/tan

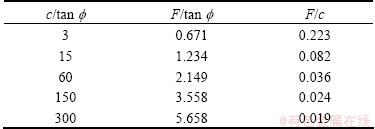
Five different values of c/tan  were also considered. The results are shown in Fig. 3 and Table 2. As c/tan increases, the critical slip surface moves towards the inside of slope and the failure mode changes from shallow slip to deep slip (local slip to global slip). F/tan  increases with the increase of c/tan , but F/c decreases.

3.2 Back analysis procedure

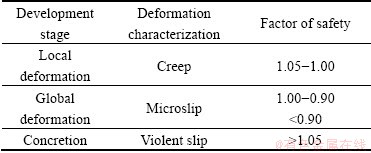
The back analysis is one where average shear strength parameters (c_a and tan _a) are calculated from the known slope geometry, unit weight and factor of safety [15]. It is recommended to select factor of safety for existing landslide based on the developing stage and deformation characteristic of landslide (Table 3) [16].

Table 3 Factors of safety for different development stages of landslide

It has been shown that for a given slope, the location of critical slip surface and value of F/tan  and F/c are related only to c/tan . Different combinations of c and 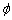 with the same value of c/tan  result in the same location of critical slip surface and value of F/tan  and F/c. We can find a specific value of c/tan  whose critical slip surface is almost consistent with the actual failure surface. This can be treated as a one-dimensional search problem, simpler than multi-variate optimization [4,5]. Bisection method is used to search the value of c/tan. The shear strength parameters of landslide slip can be determined with the known factor of safety and failure surface of existing landslide. In this work, the positional parameter L is defined to describe the position of critical failure surface. L is the horizontal distance from the vertex of the slope to the failure surface at crest, as shown in Fig. 1. The positional parameter of actual landslide L_a can be measured easily by geologic site exploration.

For inhomogeneous slope, the results by the proposed method are average shear strength parameters. If the survey region is mostly made of certain rock or soil, the parameters calculated therefore can be regarded as those of this rock or soil.

The flow chart of back analysis procedure is shown in Fig. 4. Back analysis procedure is as follows.

1) The positional parameter of landslide L_a and factor of safety F_a are obtained according to geologic site exploration.

2) One of unknown shear strength parameters is assumed as an initial value, and  is selected in this work.

3) c/tan  is searched by the bisection method, and corresponding factor of safety F and positional parameter of critical slip surface L are obtained by KEM.

4) If |L–L_a|/L_a<ε, go to step 5; otherwise, go to step 3.

5) The corresponding value of F/tan  is calculated.  is obtained based on the above finding. The friction angle of existing landslide is hence the cohesion is  

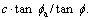
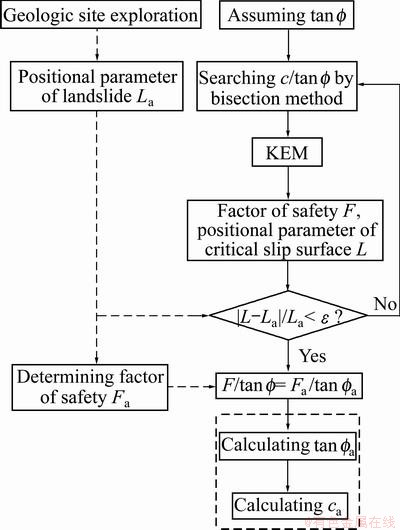
Fig. 4 Flow chart of back analysis of shear strength parameters

4 Example analysis

4.1 Example 1

The first example is a China clay pit slope shown in Fig. 5. LEY [17,18] investigated the stability of this slope, which was considered to be potentially unstable.

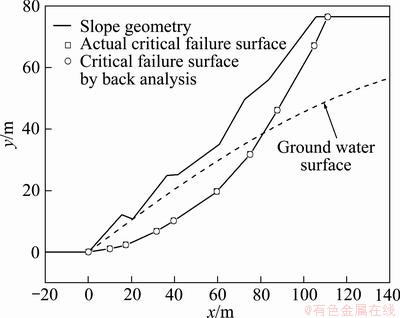
Fig. 5 Slope geometry and critical failure surface by back analysis for example 1

The properties of the material, a heavily kaolinized granite, based on direct shear tests, are listed as follows: unit weight γ=21.5 kN/m³, cohesion c=6.9 kPa, friction angle =37°. The position of groundwater surface is plotted in Fig. 5.

The location of critical failure surface obtained by KEM is shown in Fig. 5, and the corresponding factor of safety is 0.96. The accuracy of the new back analysis is verified based on a theoretical failure surface and its factor of safety by KEM. This slope is treated as a post-failure problem in which the critical failure surface and factor of safety (F_a=0.96) are known but shear strength parameters are assumed to be unknown.

The back analysis is now performed as follows. Assume =0.30, and the range of cohesion c is fixed as [0, 10 kPa]. Searching c/tan  by the bisection method, we obtain c=2.81 kPa (i.e., =9.37) and the corresponding factor of safety F=0.38. As F_a=0.96, the friction angle and cohesion of landslide slip can be determined, =0.30×0.96/0.38=0.76 (i.e., = 37.23°) and c_a=9.37×0.76=7.12 kPa. The shear strength parameters by the proposed method agree well with their correct solution with an error of less than 2%.

4.2 Example 2

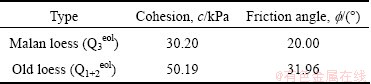
The failure accident, called Dongfeng landslide, occurred on 24 July 2003 in the right bank of Jing River, with L of 19 m [19]. The cross-section was reproduced, as shown in Fig. 6. The slope is comprised of loess, whose unit weight=18.5 kN/m³. Drill hole sampling has been carried out at crest. There are three layers in this slope, Malan loess in the upper part and old loess in the lower part. The average mechanical parameters of different soil strata based on laboratory tests are summarized in Table 4.

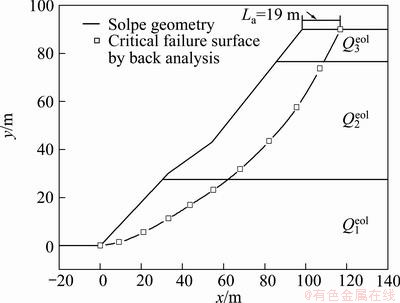
Fig. 6 Slope geometry and critical failure surface by back analysis for example 2

Table 4 Mechanical parameters of different soil strata for example 2

We assume an initial value of tan =0.35, and the range of cohesion c is fixed as [0, 100 kPa]. c=31.25 kPa (i.e., c/tan=89.28) and the corresponding factor of safety F=0.68 are obtained by the bisection method. The factor of safety at failure can be considered to be equal to unity (F_a=1.0), thus we obtain 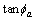=0.35×1/0.68 =0.51 (i.e., =27.02°), and c_a=89.28×0.51=45.53 kPa. The shear strength parameters by back analysis are slightly smaller than those of old loess, demonstrating the validity of the proposed method.

4.3 Example 3

Landslide is located in an open pit mining slope, with slip mass height of 112 m, slope angle before failure of 42°, and L_a of 10 m. The cross-section was reproduced, as shown in Fig. 7. Unit weight of slip mass is taken as 18 kN/m³.

Assume 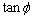=0.30, and the range of cohesion c is fixed as [0, 50 kPa]. The bisection method converges within 5 iterations, and the iterative procedure is shown in Fig. 8. The result illustrates that the proposed method has good converging speed. We obtain that c=14.06 kPa (i.e., c/tan =46.87) and the corresponding factor of safety F=0.47. The factor of safety at failure can be considered to be equal to unity (F_a =1.0), thus we obtain tan _a=0.30×1/0.47=0.64 (i.e., _a=32.62°), and c_a=46.87× 0.64=30.00 kPa.

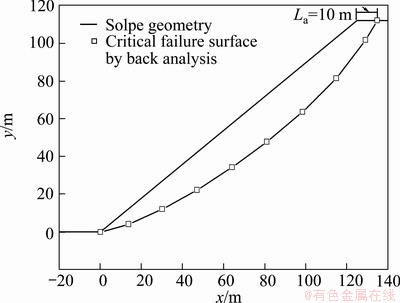
Fig. 7 Slope geometry and critical failure surface by back analysis for example 3

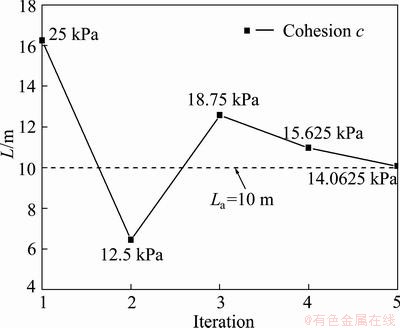
Fig. 8 Iterative process

5 Conclusions

1) When the slope geometry, unit weight and working conditions in a slope are given, the location of the critical slip surface and the value of  and  are related only to the value of .

2) A rigorous back analysis combining KEM was presented with strong theoretical background. The shear strength parameters of landslide slip can be back calculated according to the known positional parameter L and the factor of safety in a specific cross-section.

3) Three examples were given for demonstrating the validity of the new technique. The shear strength parameters obtained by back analysis are almost consistent with their correct solutions or test results.

References

[1] YAMAGAMI T, UETA Y. Back analysis of average strength parameters for critical slip surfaces [C]//BALASUBRAMANIAM A S. Proceedings of the Computer and Physical Modelling in Geotechnical Engineering. Rotterdam: Balkema, 1989: 53-67.

[2] DUNCAN J M, STARK T D. Soil strengths from back analysis of slope failures [C]//RAYMOND B S, ROSS W B. Proceedings Specialty Conference Stability and Performance of Slopes and Embank-II. Berkeley: ASCE, 1992: 890-904.

[3] WESLEY L D, LEELARATNAM V. Shear strength parameters from back-analysis of single slips [J]. Geotechnique, 2001, 51(4): 373-374.

[4] NGUYEN V U. Back calculation of slope failure by the secant method [J]. Geotechnique, 1984, 34(3): 223-227.

[5] LI Shou-ju, SHANGGUAN Zi-chang, LIU Ying-xi. Identification procedure for shear strength parameters of geotechnical materials using hybrid genetic algorithm [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 676-680. (in Chinese)

[6] JIANG J C, YAMAGAMI T. Charts for estimating strength parameters from slips in homogeneous slopes [J]. Computers and Geotechnics, 2006, 33: 294-304.

[7] JIANG J C, YAMAGAMI T. A new back analysis of strength parameters from single slips [J]. Computers and Geotechnics, 2008, 35: 286-291.

[8] GUSSMANN P. Kinematical elements for soils and rocks [C]// EISENSTEIN Z. Proceedings of 4th International Conference on Numerical Methods in Geomechanics. Edmonton: Balkema, 1982: 47-52.

[9] CAO Ping, GUSSMANN P. Kinematical element method and slope stability analysis [J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(6): 663-666. (in Chinese)

[10] GUSSMANN P. Effective KEM solutions for the limit load and the slope stability problem [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(14): 1061-1077.

[11] LI Feng, WANG Xiao-rui, LUO Xiao-hui, GUO Yuan-cheng. Assessment methods of chance constrained on bottom stability of foundation pit [J]. Rock and Soil Mechanics, 2010, 31(12): 3867-3874. (in Chinese)

[12] MICHALOWSKI R L. Stability charts for uniform slopes [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2002, 128(4): 351-355.

[13] BELL J M. Dimensionless parameters for homogenous earth slopes [J]. Journal of Soil Mechanics and Foundation Engineering Division, ASCE, 1966, 92(5): 51-65.

[14] SHI Wei-min, YE Xiao-ming, ZHENG Ying-ren. Stability analysis of step-shaped slope [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(5): 698-701. (in Chinese)

[15] DUNCAN J M, WRIGHT S G. Soil strength and slope stability [M]. Hoboken: John Wiley & Sons, 2005.

[16] XU Han-bin, WANG Jun. Selection of landslide stability factor in inverse calculation [J]. Acta Geologica Sichuan, 1999, 19(1): 86-89. (in Chinese)

[17] LEY G M M. The properties of hydrothermally altered granite and their application to slope stability in open cast mining [D]. London: London University, 1972.

[18] DUNCAN C W, CHRISTOPHER W M. Rock slope engineering [M]. Oxon: Spon Press, 2005.

[19] ZHANG Chang-liang. Study on the three-dimensional limit equilibrium of slope [D]. Xi’an: Chang’an University, 2008. (in Chinese).

边坡滑带抗剪强度参数的严格反分析方法

张 科¹，曹 平¹，保 瑞^1,2

1. 中南大学 资源与安全工程学院，长沙 410083；

2. 中国有色金属工业昆明勘察设计研究院，昆明 650000

摘  要：提出一种边坡滑带抗剪强度参数的严格反演方法。采用运动单元法求解安全系数和临界滑动面以克服极限平衡法的不足。研究抗剪强度参数组合与稳定状况间的理论关系。结果表明，c/tan 控制滑动面位置、F/tan 和F/c。随着c/tan 的增大，滑动面位置向坡内移动。基于上述研究结果，根据某个剖面的已知安全系数和滑动面位置，可快速反算滑带抗剪强度参数。将提出的方法应用于3个计算实例，用于证明本方法的有效性。反分析所得的抗剪强度参数与理论精确解和实验结果很接近。

关键词：边坡稳定；反分析；运动单元法；抗剪强度参数；临界滑动面

(Edited by Hua YANG)

Foundation item: Project (51174228) supported by the National Natural Science Foundation of China; Project (CX2012B069) supported by Hunan Provincial Innovation Foundation for Postgraduate; Project (201003) supported by Transportation Science and Technology Projects of Hunan Province, China

Corresponding author: Ke ZHANG; Tel: +86-13467530581; E-mail: zhangke_csu@163.com

DOI: 10.1016/S1003-6326(13)62617-5