文章编号：1004-0609(2016)-10-2093-09

厚壁钛管轴向压缩塑性的应力-应变关系

刘  静^{1, 2}，李兰云¹，李  霄¹，李渊博¹

(1. 西安石油大学 材料科学与工程学院，西安 710065；

2. 西北工业大学 凝固技术国家重点实验室，西安 710072)

摘  要：基于环形试样轴压实验、有限元模拟、回归分析和遗传算法相结合的反求方法对厚壁钛管压缩状态下的塑性材料参数进行快速识别，利用试验方法研究机床弹性变形时TA18厚壁钛管不同圆环压缩试样高度下试样鼓肚率和机床弹性变形的变化情况，并在此基础上确定了试样高度范围，获得了试验力-位移曲线。利用反求方法确定了其压缩应力应变关系，并将其应用在不同高度钛管环形试样轴压模拟中，与试验进行对比，以发现反求获得的应力-应变曲线可以较好地预测钛管轴向压缩变形行为，对压缩试样变形后最大直径和载荷的预测误差分别不超过1.5%和11%。

关键词：厚壁钛管；圆环压缩试样；反求方法；压缩应力状态；应力-应变关系

中图分类号：TG115　　           文献标志码：A

厚壁钛合金管零件由于具有高强重比、优越的耐蚀性及抗疲劳性，在航空航天等领域得到了广泛应用^[1-3]。塑性成形工艺获得的厚壁钛合金管件具有塑性好、强度高等特点(如挤压、旋压、拉拔)，已成为加工钛合金管材零件的主要手段^[4-5]。对管材塑性变形行为分析是确保管材精确塑性成形的前提和基础，而变形分析的可靠性往往取决于材料在变形时的力学性能，尤其是塑性应力-应变关系。由于材料的塑性应力应变关系与其所受的应力状态有关，因此，要根据具体成形过程中材料受力状态选择合适的试验方法进而确定材料的塑性参数^[6]。对于以压缩变形为主的厚壁钛管塑性成形过程，如旋压和挤压，需要确定其在压缩状态下的应力应变关系。然而由于管材的中空结构，传统的圆柱试样轴向压缩试验方法难以用来确定管材的压缩力学性能。因此，如何准确确定厚壁钛管压缩状态下的应力-应变关系已成为精确分析厚壁钛管塑性变形行为的一个关键问题。

目前，对于压缩状态下的管材材料塑性参数确定方法主要有直接试验法和反求法两种。试验法是将局部切块试样、圆环整体试样或弧形堆叠试样进行轴向压缩^[7]，由载荷位移曲线直接计算获得管材轴向的应力应变关系。其中，局部切块压缩试样在管壁上直接截取试样，受管材壁厚的影响较大，且压缩过程中容易失稳。弧形堆叠试样适用于薄壁管材，其原理与切块试样相同。区别于切块和堆叠压缩试验，整体环形试样轴向压缩试验稳定性较好，与管材塑性成形过程中的真实应力状态更为接近，得到了广泛的应用。然而，受摩擦的影响，整体环形试样在压缩过程中沿径向会发生不均匀变形，出现鼓肚现象。而管材的中空结构使得难以对试样外形进行去鼓形修整。因而，采用该试验方法时，仅能获得鼓肚发生之前小应变范围材料的压缩应力应变关系，鼓肚发生后，计算获得的应力、应变数据与实际值相差较大。而管材的塑性成型一般都属于大变形过程，需要大应变范围的应力应变关系曲线。

针对上述问题，一些学者^[8-13]提出通过将试验与解析公式(或有限元)及优化算法相结合的反求方法确定材料的应力应变关系。反求法的实质是通过试验获得力-位移曲线，然后输入假设的虚拟材料参数进行同样试验过程，获得有限元解或解析解，并将计算解与试验结果进行对比，通过算法迭代，使得计算解与试验结果满足误差要求，从而反求出材料参数。余海燕等^[8]利用单向拉伸试验结合数值模拟反求出了5052铝合金材料失效参数。肖罡等^[9]采用温热压缩实验和解析法确定6013铝合金热变形流变应力本构模型中的材料常数。孙志超等^[10]采用圆环轴压试验，结合解析法，通过反算确定铝合金管强化方程中的强度系数和应变硬化指数。该方法在建立材料参数与力-位移曲线解析关系过程中过多采用假设条件，因而其解析表述准确性对材料参数的识别精度有很大的影响。LANG等^[11]和PATHAK等^[12]分别采用深拉伸实验和圆环热轴压试验获得载荷-位移曲线，基于有限元数值模拟和反求方法获得了铝和钢的材料参数。HABRAKEN等^[13]综合利用环形试样压缩试验、有限元模拟和优化算法确定了旋转锻造空心铝棒的Hollomon硬化材料参数。上述反求方法因需要将有限元与优化方法结合计算，因此材料参数反求的效率极大程度上依赖于有限元模拟计算的时间及迭代次数。因此，一些学者提出用人工神经网络和回归分析的方法代替有限元以提高计算效率。AGUIR等^[14]和ABOUHAMZE等^[15]提出了一种基于有限元模拟、神经网络和遗传算法的混合的材料参数识别方法，并与传统的反求方法进行了对比，发现用ANN替代有限元与优化算法耦合求解目标函数后，计算时间可以显著减小。殷为洋等^[16]利用解耦型数据分组处理方法反求获得了动态载荷作用下车身的材料参数。然而，利用神经网络进行参数反求时，样本空间的大小及形式对训练结果影响较大，并且隐含层的层数和节点数较难确定^[17]。与神经网络方法相比，回归分析可以建立输入与输出之间显示的表达式，实现材料参数-宏观变形量的快速响应。LI等^[18]采用数值模拟、凸模胀形试验、克里金模型、多岛遗传算法相结合的优化方法对铝合金板材Hill’90中的各向异性材料参数进行了识别，其用克里金模型代替有限元与遗传算法进行迭代求解，从而大大提高了材料参数反求的计算效率。LIU等^[19]提出一种基于管侧压实验、数值模拟、回归分析、遗传算法相结合的反求方法来确定薄壁管材压缩应力应变关系。在该方法中，首先基于数值模拟和回归分析，建立宏观变形量和材料参数之间的显式表达式，然后采用遗传算法对材料参数进行反求迭代，直到收敛，经过与实验对比该方法预测精度和效率均比传统的反求方法高。因此可采用该反求方法确定厚壁钛管应力应变关系。然而管侧压实验中管段变形区外侧呈现拉应力状态，内侧为压应力状态，用该实验反求出的材料参数不能完全反应管材压缩状态下的应力应变关系。

因此，对厚壁钛管，需要采用圆环轴压实验进行材料参数反求。实验中发现，圆环轴压过程中由于摩擦的影响，会出现鼓肚现象，使得不同试样不同位置应力分布差别较大，为了获得较为均匀的压缩应力状态，需要选取合理的试样尺寸。CETINARSLAN^[20]和APPA等^[21]在镦粗试验时发现，增大试样的高径比可以有效的降低试样变形后的鼓肚现象。但是在管材试样轴向压缩中发现，试样高度越大鼓肚越大。这是因为对于管材压缩试样，试样与压头接触面积小，摩擦对不均匀变形的作用有限，试样鼓肚的大小主要由试样的抗失稳能力决定，而试样高度越大，试样的稳定性越差，鼓肚越明显。所以，对于管材压缩试验而言，为了降低鼓肚率并提高试验结果的准确性，需要降低试样的高度。然而，当试样高度太小时，试样鼓肚率下降，整体屈服困难，所需试验力增加。机床弹性变形占显示总变形的比例与大试样高度的情况相比会大大增加，尤其对屈服硬化指数较高的材料，机床弹性变形对试验结果的影响不容忽视。因此，在轴向压缩试验时，需要考虑机床的弹性变形。可以说，确定合适的环形试样高度是获得准确的管材压缩应力应变曲线的前提和基础。

因此，本文作者采用环形试样轴压实验、有限元模拟、回归分析和遗传算法相结合的方法对厚壁钛管压缩状态下的塑性材料参数进行快速识别。首先设计了不同高度的圆环压缩试样，分析了考虑机床弹性变形下，不同圆环压缩试样高度时机床弹性变形和鼓肚的变化情况，确定了合理的压缩试样高度范围；在该范围内，选取特定高度的试样，利用多个相同试样进行了不同压下量的压缩试验，获得了厚壁钛管的压缩载荷、最大直径；然后利用虚拟正交试验及回归分析建立了材料参数与载荷之间的显式关系，实现了管轴压载荷的快速预测；最后结合管轴压试验结果，采用遗传算法反求出了TA18厚壁钛管压缩状态下的应力应变关系，并进行试验验证。

1  实验

针对厚壁钛管压缩成形下的变形特点，本文作者提出了相对简单的实验方法，建立了基于物理模拟-正交数值模拟-回归分析-遗传算法反求获取其高精度本构关系的方法。具体步骤如下。

1) 进行不同高度圆环试样轴向压缩实验，综合考虑机床弹性变形及试样形状变化，确定合理的圆环压缩试样高度范围。

2) 选取合适高度的圆环试样进行轴向压缩实验，获得载荷-位移曲线。

3) 进行单向拉伸试验，确定应力强化类型及需要识别的参数。

4) 基于正交数值模拟和回归分析，建立宏观变形量(载荷-位移曲线)和应力应变关系中材料参数之间的显式表达式。

5) 采用遗传算法对材料参数进行反求迭代，直到收敛。

6) 确定管材压应力状态下的应力应变关系。

具体研究思路如图1所示。

1.1  试样高度范围的确定

实验选用的材料为d 14 mm×1.35 mm(外径×壁厚)的TA18中强厚壁钛管。压缩试验在材料万能试验机CMT5205上进行(最大载荷200 kN)。从管坯上截取圆环试样，将试样置于试验机平行压头之间以1 mm/min的速度进行匀速压缩，为减小摩擦，试样端面与压头之间采用拉伸油进行充分润滑，摩擦因数为0.1。

为了确定一个合适的试样高度，选取高厚比H₀/t₀={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}的环形试样，即高度H₀={1.35, 2.7, 4.05, 5.4, 6.75, 8.1, 9.45, 10.8, 12.15, 13.5} mm，进行压缩试验(见图2)，本试验中考虑机床变形。在相同的名义压下率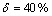(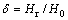)下，测量各试样的鼓肚率δ_b和机床变形率δ_m。δ_b和δ_m分别表示为

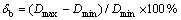                (1)

式中：D_max和D_min分别是试样变形后的最大外径和最小外径。

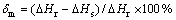                 (2)

式中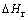：是试验机记录的压下量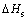；是试样的高度减小值。

鼓肚率和机床变形率随试样高度的变化如图3所示。由图3可见，在相同的名义压下率下，鼓肚率随试样高度的增大而增大。从试样均匀变形的角度讲，鼓肚率越小越好，即试样高度越小越好。然而，在试验中发现，当试样高厚比小于3 mm时，在压缩过程中，试样变形很小，很大一部分为机床变形。这是由于试样的刚度与高度有关，试样高度越小，则试样的刚度越大，抵抗变形的能力越强，此时变形主要集中在机床系统。当试样高度为1.35 mm时，机床弹性变形所占总变形的比例高达96%。而H₀/t₀＞6时，试样鼓肚情况较为严重，又很容易发生失稳，两种情况下均无法获得反求所需的足够实验数据。因此，综合考虑，针对本研究中规格为d 14 mm×1.35 mm的TA18厚壁钛管，试样高度范围为4.05~6.75 mm(高厚比H₀/t₀为3~5)时，鼓肚较小，压缩时可以获得准确、足够的实验数据，可以用来进行材料参数反求。

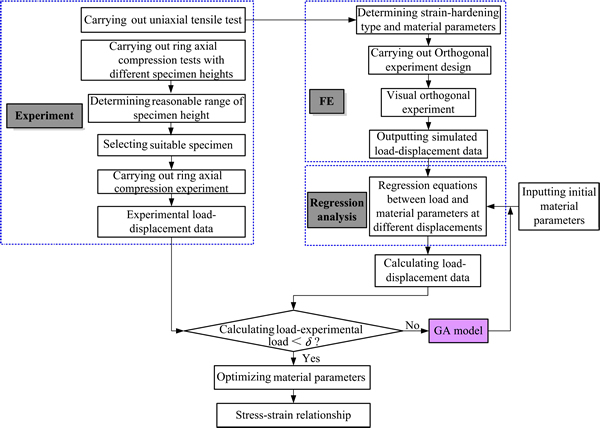
图1  厚壁钛管压应力状态下应力-应变关系建立方法分析流程图

Fig. 1  Analysis schematic diagram of research method for determining stress-strain relationship of thick-walled titanium alloy tubes

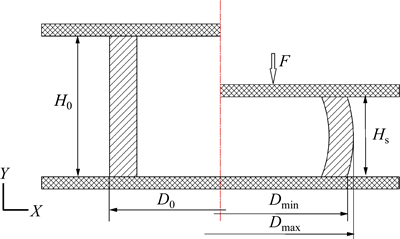
图2  圆环试样压缩变形示意图

Fig. 2  Schematic diagram of ring sample compression test

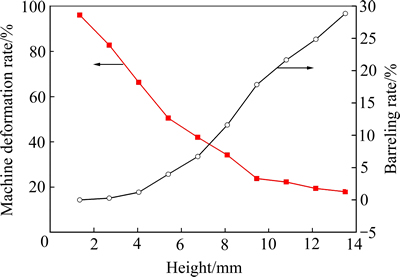
图3  机床变形率及鼓肚率随试样高度的变化

Fig. 3  Change machine deformation and barreling with sample height

1.2  压缩实验载荷变形量确定

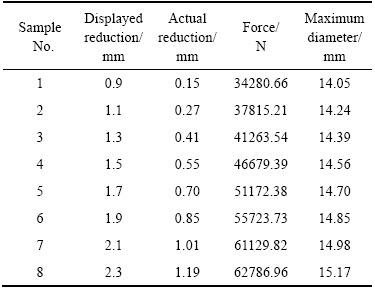
由于试验机记录的压下量并非试样的实际压缩量，因此不能直接确定各试样的压缩高度。为确定每个试样的显示压下量，首先将一个试样压缩至断裂，输出载荷位移曲线，记录塑性变形的起始点(d_p, F_p)和载荷最大值点(d_m, F_m)，然后将位移在(d_p, d_m)范围内进行离散，由此即可确定出均匀塑性变形范围内各试样的显示压下高度。根据2.1节的研究结果，选取高度为5.4 mm的环形试样进行压缩实验。试样塑性变形起始点到载荷最大点的变形量范围为0.9~2.3 mm，将位移在该范围内离散成8个等距的位移点，取8个同高度的试样分别压下相应的变形量，实验测量的压下量、载荷、最大直径如表1所列。

表1  高度5.4 mm的圆环试样的压缩实验结果

Table 1  Experiment results of TA18 tube with 5.4 mm height specimen in compression test

2  钛管压缩应力-应变关系反求

根据文献[19]参数反求方法，对于d 14 mm×1.35 mm的TA18厚壁钛管，首先进行整管单向拉伸试验，获得单拉应力状态下的应力应变，拟合后发现应力应变关系符合Swift强化方程，即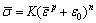，单拉应力状态材料参数分别为K=991.91，n=0.0877, 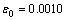。因此，TA18钛管压缩状态下强化模型为Swift强化类型，需要识别的参数包括强度系数K、应变硬化指数n和初始应变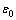。根据单拉实验结果确定的TA18管反求材料参数变化范围及水平如表2所示。对于三因素四水平的正交实验选用L₁₆(4⁵)正交表。

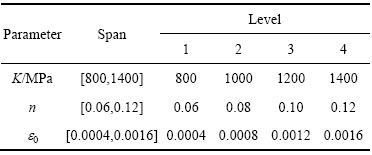
表2  TA18管材料参数选取范围及水平

Table 2  Spans and levels of material parameters for TA18 tube

基于ABAQUS/Explicit平台建立圆环轴向压缩有限元模型，试样高度为5.4 mm(见图4)。材料满足Mises各向同性屈服准则。由于管壁较厚，采用实体单元C3D8R进行离散；将模具视为刚体，采用刚体壳单元R3D4进行离散。试样与压头接触面之间满足库伦摩擦模型，摩擦系数为0.1。在压头的几何中心设置参考点，上压头参考点的自由度完全约束，下压头参考点仅开放y方向的自由度。进行虚拟正交试验，模拟获得的不同材料参数组合下的16组载荷-变形曲线如图5所示。可以发现实验数据点在模拟载荷变形曲线范围内，因此正交试验安排合理。按照表1中的实验压下量，在位移d_k (k=0.15, 0.27, …, 1.19)处，可以获得8组载荷-材料参数数据。

 

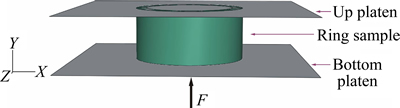
图4  厚壁钛管轴向压缩有限元模型

Fig. 4  FE model for thick-walled tube axial compression

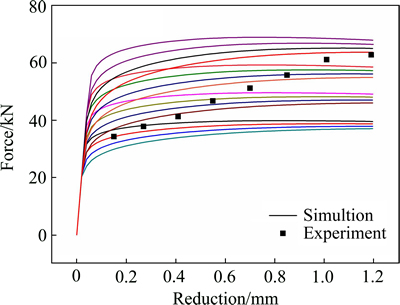
图5  虚拟正交试验获得的载荷-变形曲线

Fig. 5  Load-reduction curves obtained by virtual orthogonal test

根据虚拟正交试验结果建立载荷-材料参数之间的回归方程。首先进行极差分析，通过考察影响参数对载荷的水平响应，发现K的水平响应近似满足线性关系，n和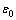均近似满足二次抛物线性质，如图6所示。

因此，对K取一次项，对n和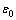取二次项，同时，考虑两两参数之间的交互作用，位移d_k处的载荷与材料参数之间的关系可表示为如下形式：

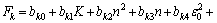
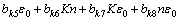            (3)

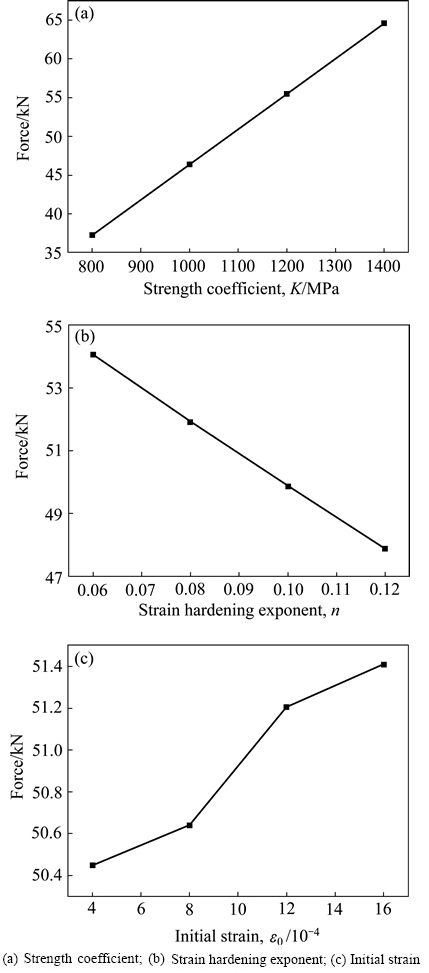
图6  影响参数对载荷的水平响应 (实际压下量0.55 mm处)

Fig. 6  Visual representation of orthogonal parameters on force (actual reduction 0.55 mm)

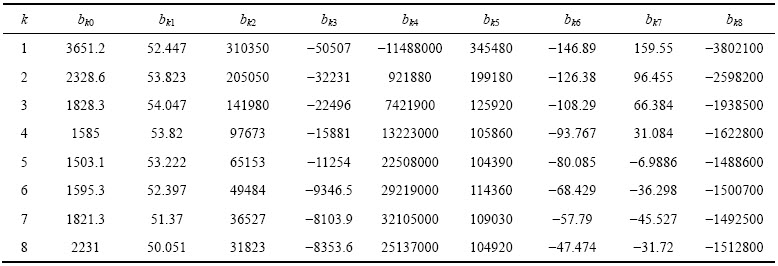
利用正交表中的模拟数据，采用基于Matlab编译的多元非线性回归程序进行拟合，获得方程(3)中的各回归系数，如表3所列。

为了进一步验证回归模型的可靠性，另取4组不同于正交表中的材料参数组合(见表4)进行模拟实验。图7所示为模拟及回归模型获得的载荷-压下量曲线。

表3  TA18钛管载荷-材料参数回归方程系数

Table 3  Coefficients of load-material parameter regression equations of TA18 tube

由图7可见，回归方程的预测误差小于0.21%。因此，回归方程精度较高，可以用于管材环形试样轴向压缩实验的载荷预测。

将上述实验值输入到载荷预测回归方程中，用Matlab的GA工具箱对回归公式中的材料参数进行反求。GA模型的参数为：种群大小200，迭代次数500，交叉率0.95，变异率0.01。采用GA算法反求出的优化的材料参数如表5所列。

表4  TA18钛管载荷-材料参数回归方程检验数据

Table 4  Testing database for load-material parameter regression equation of TA18 tube

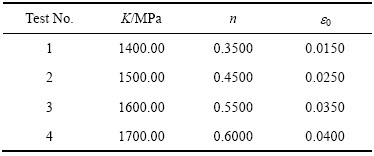
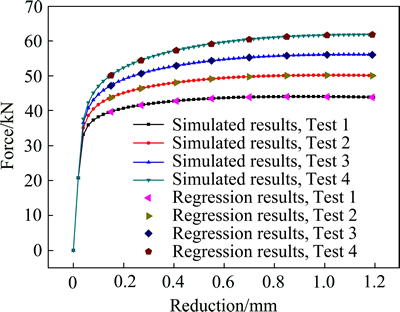
图7  模拟结果与回归方程计算结果对比

Fig. 7  Comparison of simulated and regression results

表5  识别的TA18钛管压缩应力状态下的材料参数

Table 5  Identified material parameters of TA18 tube under compressive stress state

为了验证所识别参数的准确性，利用反求出的材料参数进行圆环轴向压缩有限元模拟，并将模拟获得的载荷及试样最大直径与实验值进行对比，如图8所示。由图8可以看出，预测载荷与实验值的误差小于9.0%，模拟最大直径与实验值最大误差为0.8%。因此，反求出的材料参数精度较高，认为其可以反映材料在压缩状态下的力学性能。

为进一步考察所确定的钛管压缩应力应变关系的准确性及适应性，将反求获得的材料参数用于高度为4.05 mm和6.75 mm的圆环试样压缩模拟，并将变形后的试样轮廓、最大直径、载荷与实验值进行了对比。

图9所示为不同压下量下模拟和试验获得的试样轮廓。由图9可见，在不同的塑性变形程度下模拟获得的压缩试样轮廓与试验非常接近。并且由模拟压缩试样的应力分布云图可见，随着塑性变形的增大，应力分布不均匀程度增大，导致试样的鼓肚现象变得更加明显。

图10所示为模拟和试验测得的试样最大直径随压下量的变化曲线。由图10可见，随着压下量的增大，试样最大直径呈线性增大，模拟与试验获得的不同压下量的最大直径非常接近。对于高度为4.05 mm和6.75 mm的试样，最大误差分别为0.8%和1.5%，且均出现在压下量较大时，因此，确定的材料参数能准确反映圆环在压缩过程中的直径变化。

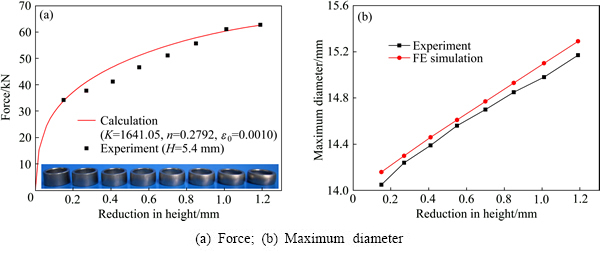
图8  模拟及实验获得的TA18钛管环形试样轴压结果对比

Fig. 8  Comparison of simulated and experimental results for TA18 ring sample axial compression

图9  模拟及试验的压缩试样轮廓对比

Fig. 9  Comparison of simulated and experimental sample profiles at different reductions

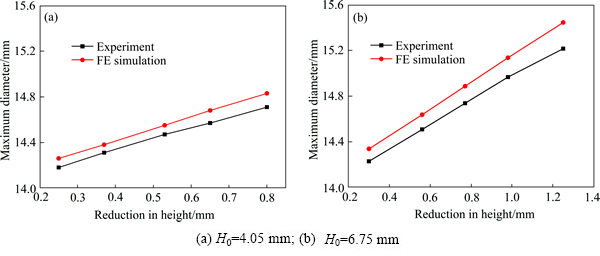
图10  不同压缩量下模拟及试验的压缩试样最大直径对比

Fig. 10  Comparison of maximum diameters of deformed ring sample obtained by simulation and experiment

图11所示为模拟及实验的圆环压缩载荷-位移曲线对比。由图11可见，模拟与实验获得的载荷-位移曲线比较接近。对于高度为4.05 mm的试样，载荷的最大预测误差为6.2%。对于6.75mm高的试样，由于高度较大，容易发生鼓肚，随着压下量的增大，误差逐渐增大，但最大误差仍小于11%。

由以上分析可知，反求出的材料参数可以比较准确地描述厚壁钛管压缩状态下的变形行为，且该研究方法在确定厚壁管材压缩状态下应力应变关系方面具有普适性。

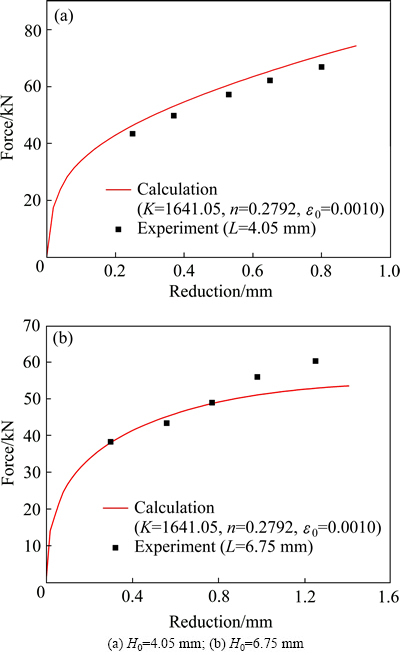
图11 模拟及实验获得的圆环压缩载荷-位移曲线对比

Fig. 11  Comparison of simulated and experimental load- displacement curves

3  结论

1) 利用实验方法研究了圆环压缩实验中试样高度对鼓肚和机床弹性变形的影响，确定了规格为d 14 mm×1.35 mm的TA18厚壁钛管环形压缩试样高度范围。

2) 利用环形试样压缩实验结合有限元模拟、回归分析和遗传算法确定了TA18管的压缩状态下的Swift强化方程中的材料参数。将该材料参数用于不同高度环形试样轴向压缩过程模拟，并与试验进行了对比，发现试样压缩后最大直径的预测误差小于1.5%，载荷的预测误差小于11%。

REFERENCES

[1] ADIB A M L, BAPTISTA A R P, BARBOZA M J R, HAGA C, MARQUES C C F. Aircraft engine bleed system tubes: Material and failure mode analysis[J]. Engineering Failure Analysis, 2007, 14: 1605-1617.

[2] BOYER R R. An overview on the use of titanium in the aerospace industry[J]. Materials Science and Engineering A, 1996, 213: 103-114.

[3] 金和喜, 魏克湘, 李建明, 周建宇, 彭文静. 航空用钛合金研究进展[J]. 中国有色金属学报, 2015, 25(2): 280-292.

JIN He-xi, WEI Ke-xiang, LI Jian-ming, ZHOU Jian-yu, PENG Wen-jing. Research development of titanium alloy in aerospace industry[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 280-292.

[4] YANG H, ZHAN M, LIU Y L, XIAN F J, SUN Z C, LIN Y, ZHANG X G. Some advanced plastic processing technologies and their numerical simulation[J]. Journal of Materials Processing Technology, 2006, 177: 192-196.

[5] ZHAN Mei, ZHAI Hua-dong, YANG He. Springback mechanism and compensation of cryogenic Ti alloy tube after numerically controlled bending[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S2): s287-s293.

[6] KUWABARA T. Advances in experiments on metal sheets and tubes in support of constitutive modeling and forming simulations[J]. International Journal of Plasticity, 2007, 23: 385-419.

[7] AZHIKANNICKAL E, JAIN M, BRUHIS M. Test methods for the determination of the stress-strain behaviour of oriented polypropylene (OPP) tubes in uniaxial compression[J]. Polymer Testing, 2007, 26: 195-201.

[8] 余海燕, 王 友. 5052铝合金冲压成形过程中韧性断裂的仿真研究[J]. 中国有色金属学报, 2015, 25(11): 2975-2981.

YU Hai-yan, WANG You. Bulging simulation of ductile fracture of 5052 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(11): 2975-2981.

[9] 肖 罡, 李落星, 叶 拓. 基于材料参数修正的铝合金热变形本构模型优化[J]. 中国有色金属学报, 2014, 24(6): 1393-1400.

XIAO Gang, LI Luo-xing, YE Tuo. Optimization of constitutive equation during hot deformation of 6013 aluminum alloy based on modified material parameters[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1393-1400.

[10] 孙志超, 杨 合, 蔡 旺, 林 艳. 一种确定管材塑性本构关系的反算法[J]. 重型机械, 2000(3): 43-46.

SUN Zhi-chao, YANG He, CAI Wang, LIN Yan. An inverse method for determining plastic constitutive relationship of tubes[J]. Heavy Machinery, 2000(3): 43-46.

[11] LANG Li-hui, LI Tao, ZHOU Xian-bin, KRISTENSEN B E, DANCKERT J, NIELSEN K B. Optimized constitutive equation of material property based on inverse modeling for aluminum alloy hydroforming simulation[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(6): 1379-1385.

[12] PATHAK K K, KOTWAL C P, NARAYAN S P, RAMAKRISHNAN N. Reverse engineering of a hot ring compression test using FEM[J]. Indian Journal of Engineering and Materials Sciences, 2004, 11: 189-192.

[13] HABRAKEN A M, BOUFFIOUX C, CARTON M, LECOMTE-BECKERS J. Study of a 2024 aluminium rod produced by rotary forging[J]. Journal of Materials Processing Technology, 2007, 184: 19-26.

[14] AGUIR H, BELHADJSALAH H, HAMBLI R. Parameter identification of an elasto-plastic behaviour using artificial neural networks-genetic algorithm method[J]. Materials and Design, 2011, 32: 48-53.

[15] ABOUHAMZE M, SHAKERI M. Multi-objective stacking sequence optimization of laminated cylindrical panels using a genetic algorithm and neural networks[J]. Composite Structures, 2007, 81: 253-263.

[16] 殷为洋, 王 琥, 冯 慧, 汤 龙. 基于解耦型GMDH的车身材料参数反求[J]. 中国机械工程, 2015, 26(9): 1215-1221.

YIN Wei-yang, WANG Hu, FENG Hui, TANG Long. Inverse determination of material parameters based on decoupled GMDH algorithm[J]. China Mechanical Engineering, 2015, 26(9): 1215-1221.

[17] KAPOOR R, PAL D, CHAKRAVARTTY J K. Use of artificial neural networks to predict the deformation behavior of Zr-2.5Nb-0.5Cu[J]. Journal of Materials Processing Technology, 2005, 169: 199-205.

[18] LI Xiao-qiang, HE De-hua. Identification of material parameters from punch stretch test[J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1435-1441.

[19] LIU Jing, YANG He, LI Hong-wei, LI Heng, ZHU Shuai. A new hybrid identification method for determining the material parameters of thin-walled tube under compressive stress state[J]. Materials and Design, 2013, 44: 49-58.

[20] CETINARSLAN C S. Effect of aspect ratio on barreling contour and variation of total surface area during upsetting of cylindrical specimen[J]. Materials and Design, 2007, 28: 1907-1913.

[21] APPA R J, BABU R J, KAMALUDDIN S, SARCAR M M M, BHARGAVA N R M R. Studies on cold workability limits of pure copper using machine vision system and its finite element analysis[J]. Materials and Design, 2009, 30: 2143-2151.

Plastic stress-strain relationship of thick-walled titanium alloy tube under compressive stress state

LIU Jing^{1, 2}, LI Lan-yun¹, LI Xiao¹, LI Yuan-bo¹

(1. School of Materials Science and Engineering, Xi’an Shiyou University, Xi’an 710065, China;

2. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract: An inverse method for fast and accurate identifying the material parameters of thick-walled titanium alloy tube under compressive stress state was developed combing ring axial compression test, FE method, regression analysis and genetic algorithm. Considering the evitable elastic deformation of testing machine, the specimen barreling and machine elastic deformation were examined in testing thick-walled TA18 tube specimen with varying heights. Then, a reasonable range of specimen height and the experimental load-displacement curves were determined accordingly. Employing the curves, the material parameters of tube were obtained by using the inverse method. In order to verify the reliability of the identified parameters, FE simulations of ring compression tests were carried out using the determined material parameters and compared with experiments. Comparison results show that the obtained stress-strain curves can describe the compressive deformation behaviors of tube material with prediction errors of maximum diameter, and the load deviates from the experiments less than 1.5% and 11%, respectively.

Key words: thick-walled titanium alloy tube; ring compression specimen; reverse method; compressive stress state; stress-strain relationship

Foundation item: Project(51405386) supported by the National Natural Science Foundation of China; Project (2014JQ7237) supported by the Natural Science Basic Research Plan in Shaanxi Province, China; Projects(14JK1565, 15JK1575) supported by the Scientific Research Program Funded by Shaanxi Provincial Education Department, China; Project(SKLSP201403) supported by the State Key Laboratory of Solidification Processing in Northwestern Polytechnical University, China; Project(2015QNKYCXTD02) supported by the Young Innovation Research Team in Xi’an Shiyou University, China

Received date: 2015-12-28; Accepted date: 2016-04-10

Corresponding author: LIU Jing; Tel: +86-13720455151; E-mail: jingliu@xsyu.edu.cn

(编辑  李艳红)

基金项目：国家自然科学基金资助项目(51405386)；陕西省自然科学基础研究计划项目(2014JQ7237)；陕西省教育厅专项科研计划项目(14JK1565，15JK1575)；西北工业大学凝固技术国家重点实验室开放课题资助项目(SKLSP201403)；西安石油大学青年科研创新团队资助项目(2015QNKYCXTD02)

收稿日期：2015-12-28；修订日期：2016-04-10

通信作者：刘  静，讲师，博士；电话：029-88382607；E-mail: jingliu@xsyu.edu.cn