J. Cent. South Univ. Technol. (2009) 16: 1014-1021

DOI: 10.1007/s11771-009-0168-2

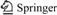
Effect of vertical load difference on cracking behaviors in

multistory masonry buildings and numerical simulation

CHEN Da-chuan(陈大川), SHANG Shou-ping(尚守平), ZHANG Cheng-qiang(张成强)

 (College of Civil Engineering, Hunan University, Changsha 410082, China)

Abstract: To investigate the causes of cracks in multistory masonry buildings, the effect of vertical load difference on cracking behaviors was investigated experimentally by testing and measuring the displacements at the testing points of a large sized real masonry U-shaped model. Additionally, the cracking behaviors in U-shaped model were analyzed with shear stress and numerical simulated with ANSYS software. The experimental results show that the deformation increases with the increase of the vertical load. The vertical load results in different deformation between the bearing wall and non-bearing wall, which leads to cracking on the non-bearing wall. The rapid deformation happens at 160 kN and cracks occur firstly at the top section of non-bearing wall near to the bearing wall. New cracks are observed and the previous cracks are enlarged and developed with the increase of vertical load. The maximum crack opening reaches 12 mm, and the non-bearing wall is about to collapse when the vertical load arrives at 380 kN. Theoretical analysis indicates that the shear stress reaches the maximum value at the top section of the non-bearing wall, and thus cracks tend to happen at the top section of the non-bearing wall. Numerical simulation results about the cracking behaviors are in good agreement with experiments results.

Key words: vertical load difference; cracking; deformation; multistory masonry building

1 Introduction

Masonry building has been a kind of mainly building structure in the past decades, which is used for residence, school, administration, hospital and hotel in China. Cracking occurred in masonry building has been arisen lots of attention all over the world. Cracks in masonry structure affect the appearance of buildings, and more importantly, the safety of building and human life. Thus, lots of work has been done to study the cracking behaviors and related mechanisms. MASSART et al[1] investigated the damage and failure phenomenon with mathematic models and simulation, and found that damage orientations masonry structures are intimately related to the initial periodic structure of the material. Some simulation methods and numerical analyses on the structure of masonry walls were proposed in Refs.[2-3]. PINTUCCHI and ZANI[4] investigated the effects of material and geometric non-linearity on the collapse of masonry structure. The influences of load on the stability and cracking behavior of masonry structures were considered in Refs.[5-7] and some experiments were done for this purpose[8-9]. Most literatures indicate that the cracks in masonry buildings are resulted from temperature variation, improper design, and subsidence[10-13]. However, most of researchers considered meso-structure of masonry wall or investigated the cracks and cracking behavior with a small-sized real masonry model. So far, there has been no experimental investigation on a large-sized real masonry structure, and the investigation on cracks related to the bearing of the structure is limited. However, in the practical engineering, it is found that cracking happens even without the influence of temperature and design, especially in the multistory masonry structures. This suggests that there must have been some other causes for cracking and failure of masonry structures. In fact, in the construction and operation process, the loads on the bearing and the non-bearing walls are different. The load on the non-bearing wall only bears the load from the walls of upper stories. But the load on the bearing wall includes the load from the walls of upper stories, the gravity of floors and living load in the construction and application. The difference increases with the increase of the height of masonry buildings. Therefore, in this work, a large-sized real U-shaped masonry model was established to study the deformation and cracking behaviors in multistory masonry buildings with the influence of different vertical loads. In addition, the maximum shear stress in U-shaped model was theoretically analyzed. Numerical simulation was also carried out to compare with the experiments.

2 Experimental

In contrast to previous work[1-4], a large-sized real U-shaped masonry model with a wall height of 4.2 m was made in order to present the practical engineering situation more accurately. Fig.1 illustrates the outline of the U-shaped model, the force loading and deformation measuring system. The large-sized real U-shaped masonry model was composed of three walls. The left and right side walls were the no-bearing walls. The bearing wall was between the two non-bearing walls and connects with non-bearing walls. A vertical load was applied to the bearing wall with an oil jack to simulate the load from the structure as mentioned above. It was worth mentioning that, to meet the building code on the ratio of height to width of masonry structure, reinforced concrete slab with a thickness of 60 mm was built crossing the two non-bearing walls at a height of 2.1 m

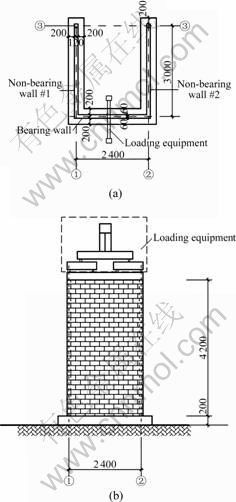
Fig.1 Plane plot of U-shaped masonry model (a) and elevation of bearing wall (b) (Unit: mm)

from the ground.

In experiments, the vertical load was gradually applied to the bearing wall. The initial load was 40 kN, and was kept 40 kN increments at each step until the loads reached 200 kN. Then, the load gradually increased with an increment of 50 kN. The loading test was continued till severe cracks occurred on the two non-bearing masonry walls, and then terminated when the non-bearing wall was about to collapse. The loads were picked up from the load cell in the actuator, while the deformation on the bearing wall and non-bearing walls was measured using displacement transducers. The testing points were reasonably distributed on the bearing wall and non-bearing walls, as shown in Fig.2. Three testing points S1, S2, and S3 were placed at the top of the bearing wall. Three testing points R1, R2, and R3 were placed at the top of the non-bearing wall #1, and three testing points T1, T2, and T3 were located at the top of the non-bearing wall #2. The others were located at the center and base of the bearing and non-bearing masonry walls, among which twelve were placed at the center of the masonry wall. The displacements of the testing points were monitored during the step-loading test.

Fig.2 Testing points and their distribution on U-shaped masonry model (·—Testing points)

The U-shaped masonry model was built up with clay bricks and mortar. The clay brick was the widely used standard brick with a size of 240 mm×115 mm×53 mm. The brick strength at factory was MU10. The mortar was the mixed cement and lime with sand in certain proportion according to the Chinese traditional process. The way of laying bricks for the model was to alternate brick layers with one in transverse direction and another in longitudinal direction. Both of mortar mixing and brick laying methods met the requirements of current Chinese building design and construction codes. 10 pieces of bricks were chosen for the strength test, and the tested average strength was 9.26 MPa. 12 mortar cubes (70.7 mm×70.7 mm×70.7 mm) were made for the mortar strength test. The average mortar strength was 5.1 MPa. All the strengths were tested according to the National Materials Testing Code of GBJ129—90.

3 Results and discussion

The load—displacement curves of testing points at the top of bearing wall are listed in Table 1. The displacement increases with the increase of the load at all the testing points. From the comparison, it is found that the tested displacements at S1, S2, and S3 exhibit a small difference at the beginning of loading. However, when the applying load reaches 160 kN, the displacements at S1 and S2 rapidly go up, especially the displacement at test point S2 is about as twice as that at 120 kN. When the applying load reaches 200 kN, the displacement at testing point S3 exhibits large variation. The displacement increases from 0.28 (160 kN) to 0.58 mm (200 kN). These results suggest that cracks may happen when a rapid increase of displacement happens at a specific load. And the rapid increase of the deformation firstly happens at the ends of the bearing wall, which are connected to the non-bearings. When the load is more than 200 kN, the deformation at testing points S1 and S3 is larger than that of testing point S2. This indicates that the deformation at the cross section of bearing wall and non-bearing wall is larger than that of the middle section of the bearing wall.

Table 1 Load—displacement data of testing points at top of thebearing wall

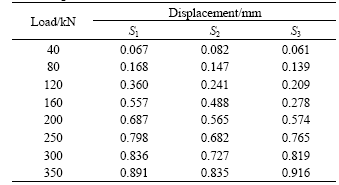
Table 2 lists the recorded loads and the relevant vertical displacements of the testing points at the top of the non-bearing walls #1 and #2. It is found that the displacement increases with the increase of load at all the testing points. The largest displacement always occurs at the testing points near the bearing wall at each load level. It is clear that the increasing rate at 160 kN of T2 is larger (see Table 2), which indicates that displacement varies rapidly and cracks on the non-bearing wall may occur at this load. The rapid increase of the displacement of testing point R2 happens at 200 kN. There are some negative values of displacement at testing points T1 and R1 because one side of the U-shaped model is open.

Table 2 Load—displacement data of testing points at top of non-bearing walls #1 and #2.

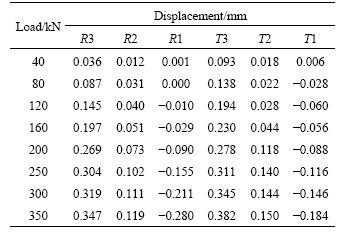
Comparing the displacement results of the bearing wall to that of the non-bearings walls, it is easy to find that the deformation resulting from the vertical load difference on the bearing and non-bearing walls are quite different. The deformation on the bearing wall is bigger than that on the non-bearing wall at the same load level. The deformation difference on bearing and non-bearing walls will result in a down-side drawing force (tensile stress) on the non-bearing walls, and finally lead to the cracking on the non-bearing walls. It is also interesting to find that the rapid displacement happens at testing points S3 and T2 under the same load of 160 kN, and the rapid displacement happens at testing points S1 and R2 under the same load of 200 kN. This suggests that the first crack may happen on the non-bearing wall #2, and the cracking site should be between testing points S3 and T2. This is confirmed by the tested cracking behavior and development processes on the non-bearing walls #1 and #2.

Figs.3 and 4 illustrate the cracking behavior and development processes on the non-bearing walls #1 and #2 based on the load—deformation data of the testing points distributed on the non-bearing walls. It is clearly seen that the first crack on non-bearing wall #2 occurs at the load of 160 kN. It is confirmed by the load—displacement result of testing point S1 on the bearing wall, where the displacement rapidly increases to 0.558 mm. When the load reaches 200 kN, cracking appears on the non-bearing wall #1, while new cracks appear on the non-bearing wall #2. The displacement at S3 (0.569 mm)

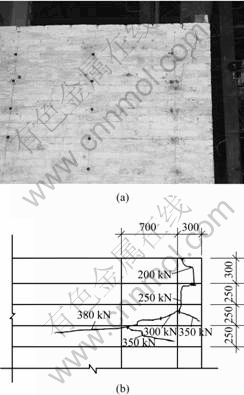
Fig.3 Cracks and crack development with loads on non-bearing wall #1: (a) Cracks on non-bearing wall #1; (b) Crack development with loads on non-bearing wall #1

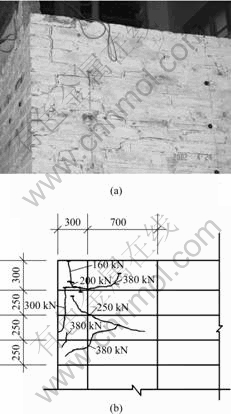
Fig.4 Cracks and crack development with loads on non-bearing wall #2: (a) Cracks on non-bearing wall #2; (b) Crack development with loads on non-bearing wall #2

happens to be identified with the value of S1 (0.558 mm) when the first crack on non-bearing wall #2 appears. The critical deformation is about 0.56 mm. It can be found from Fig.3 and Fig.4 that the deformation goes further along the direction from the top to the bottom within a width of 300 cm. When the vertical load increases to 250 kN, the first crack develops into two cracking lines. And when the load increases to 300 and 350 kN, respectively, new cracks are developed from previous cracks like tree branch. The developing direction of cracks is from top to the center and bottom of the non-bearing walls, and from the side near the bearing wall to the opposite side. The cracking area of deformation is more than 1 m².

Figs.3(a) and 4(a) indicate that the two non-bearing walls will collapse when the applied vertical load increases up to 380 kN, while the cracks are enlarged and developed further from the top to the center and bottom of the non-bearing walls. The maximum crack opening reaches 12 mm. Meanwhile, no cracks were observed on the bearing wall. But the bearing wall moved outward slightly.

4 Modeling and theoretical analysis

Based on the experiments mentioned above, it is clear that the vertical load difference between the bearing and non-bearing walls plays an important role on the cracks and crack development in multistory masonry building. Therefore, a mathematical model is proposed for the theoretical study on the established real U-shaped masonry.

The mathematical model is composed of two ideal walls q₁ and q₂ as bearing wall and non-bearing wall respectively (see Fig.5). The thicknesses of q₁ and q₂ are t₁ and  t₂. The widths of q₁ and q₂ are l₁ and l₂, the heights of q₁ and q₂ are H, and the bearing vertical loads are F₁ and F₂, respectively.

For the simplicity, the following assumptions are made.

(1) The cross-section of the vertical interface of q₁ and q₂ is an ideal friction plane.

(2) The vertical loads on q₁ and q₂ are homogeneous.

(3) On the ideal friction plane, shear stress τ is proportional to the vertical displacement difference u, and τ is given by Eq.(1)[14], where c_y is the friction coefficient in the vertical direction, and is decided by the construction materials.

τ=-c_yu                                     (1)

Taking a unit of d_y at the height of y from the ideal friction plane as shown in Fig.6, we obtain

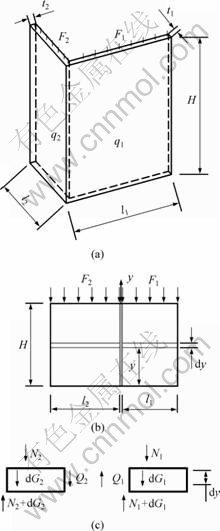
Fig.5 Mathematical model and mechanics analysis of unit: (a) Mathematical model; (b) Calculation-analysis model; (c) Analytical unit

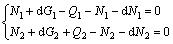              (2)

where  dG₁ and dG₂ are the self-weights of cells G₁ and G₂; Q₁ and Q₂ are shear stresses of units 1 and 2; N₁ and N₂ are forces applied on units 1 and 2, respectively.

Defining dG₁=l₁?ρ₁?t₁?dy, dG₂=l₂?ρ₂?t₂?dy, Q₁=τ₁?t₁?dy, Q₂=τ₂?t₂?dy, dN₁=l₁?t₁?dσ_1y, and dN₂=l₂?t₂?dσ_2y, where ρ₁, ρ₂ are the densities of G₁ and G₂, respectively.

Substituting the corresponding parameters into Eq.(2), we obtain

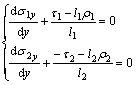                   (3)

Defining u₁ and u₂ as the displacements of q₁ and q₂ at the height of y, respectively, then we have

τ=-c_y(u₁-u₂)                                 (4)

According to the strain-stress relationship[15], 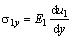 and 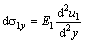, and substituting Eq.(4) into Eq.(3), we obtain

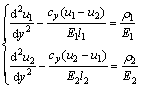                     (5)

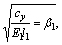
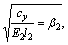
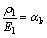
Defining 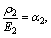and substituting them into Eq.(5), then the solutions of u₁ and u₂ are given as

(6)

where  c₁ and c₂ are coefficients, and ,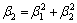

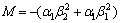
Based on the following boundary conditions, it is found that:

(1) when y=0, u₁=u₂=0, τ=0;

(2) when y=H, 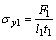,,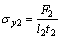 then we obtain

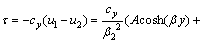
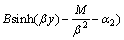                        (8)

In practical engineering, the construction materials of bearing and non-bearing walls in masonry buildings are the same, so, ρ₁=ρ₂, E₁=E₂. Meanwhile, because f(y)=cosh(βy), g(y)=sinh(βy) are monotonous increasing functions within [0, h], Hence, Eq.(8) reduces to

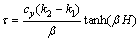                      (9)

Eq.(9) indicates that shear stress τ increases with the increase of height H. When y=H，shear stress τ reaches τ_max. τ_max is as follows:

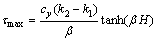                   (10)

The theoretical analyses indicate that shear stress τ reaches the maximum value at the roof section of a masonry building due to the vertical load difference between bearing and non-bearing walls. Therefore, cracking tends to firstly happen at the roof section. This is in a good agreement with the experimental results as shown in Figs.3 and 4, as well as the phenomena in practical engineering.

5 Numerical simulations

In this work we also adopted ANSYS software to simulate the load-displacement behavior of U-shaped model. The geometric parameters of the calculation model are the same as those of the U-shaped model of experiments (see Fig.2). For the simplicity, the following assumptions are made.

(1) The whole U-shaped model is regarded as an objective. The materials property (strain—stress relation- ship) of the calculation unit is the same as that of the U-shaped model, which is measured and decided by the experiments.

(2) The calculation unit is a four-point elastic shell143 as shown in Fig.6. The cracking should occur at the location with the maximum shear stress. The crack development direction is along the direction of the maximum stress.

Fig.6 Schematic diagram of plane of shell143

The calculation mesh of the U-shaped model is projection meshed, as shown in Fig.8. In the calculation, the load is applied to the top of the bearing wall as the experiments, and the applied load is uniformly distributed. The strain—stress relationship for cal- culation is given as follows:

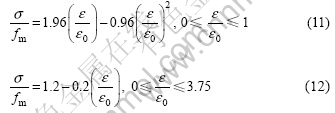
where  f_m is 3.466 MPa tested from experiment result,  Poisson ratio is 0.15, and the tensile strength of the model is of 0.38 MPa. In the calculation, the load is applied to the bearing wall as the experiments.

Fig.7 Mesh of U-shaped model

The numerical simulation results are shown in Fig.8. It can be seen from Fig.8 that the first crack on non-bearing wall #2 will occur when the load reaches  160 kN. The first crack on non-bearing wall #2 is enlarged and developed with the increase of the vertical load. The cracks are developed further downward on the non-bearing walls from the side near the bearing wall to the opposite side of the bearing wall. This indicates that the ANSYS analysis is in a good agreement with the experiment, and the established numerical model is reasonable and practical.

6 Conclusions

(1) To study the deformation and cracking behaviors in multi-story masonry buildings under the influence of different vertical load between the bearing and non-bearing walls a large sized real U-shaped masonry model is established. In the U-shaped real masonry structure, vertical load applied on the bearing wall leads to the deformation difference between the bearing and non-bearing walls. The deformation on the bearing wall is larger than that of the non-bearing walls. This results in cracking in multistory masonry buildings when the vertical load reaches a critical load and the displacement is about 0.56 mm. Therefore, vertical load difference plays an important role in cracking and crack development of multistory masonry building besides the

Fig.8 Displacement and deformation (mm) of U-shaped model at different loads: (a) 40 kN; (b) 80 kN; (c) 100 kN; (d) 150 kN;    (e) 200 kN; (f) 250 kN; (g) 300 kN; (h) 350 kN

effects of temperature variation, improper design, and subsidence.

(2) The cracking tends to happen at the roof section of the non-bearing wall, especially at the position near the bearing wall because at the roof section the shear stress reaches the maximum as theoretical analysis. Cracks are enlarged and developed with the increase of vertical load. The crack developing direction is from top to the center and bottom of the non-bearing walls, and from the side near the bearing wall to the opposite side. The maximum crack opening reaches 12 mm and the non-bearing walls will collapse when the vertical load arrives at 380 kN.

(3) Numerical simulation is in a good agreement with the experimental work. This suggests that the proposed numerical model is reasonable and practical, and helpful for the better and reliable design of multistory masonry structure.

Acknowledgement

The authors would like to thank Mr. WANG Xiang-jun for his kind help during the experiments.

References

[1] MASSART T J, PEERLINGS R H J, GEERS M G D. An enhanced multi-scale approach for masonry wall computations with localization of damage[J]. International Journal for Numerical Methods in Engineering, 2007, 69(5): 1022-1059.

[2] SPENCE S M J, GIOFFR? M, GRIGORIU M D. Probabilistic models and simulation of irregular masonry walls[J]. Journal of Engineering Mechanics, 2008, 134(9): 750-762.

[3] WU Cheng-qing, HAO Hong. Derivation of 3D masonry properties using numerical homogenization technique[J]. International Journal for Numerical Methods in Engineering, 2006, 66(11): 1717-1737.

[4] PINTUCCHI B, ZANI N. Effects of material and geometric non-linearities on the collapse load of masonry arches[J]. European Journal of Mechanics, A Solids, 2009, 28(1): 45-61.

[5] WANG Shu-hong, TANG Chun-an, ZHU Fu-sheng. Numerical modeling and analysis of masonry micro-cracks[J]. Journal of Building Structure, 2003, 24(2): 64-69.(in Chinese).

[6] MILANI G, LOURENCO P, TRALLI A. Homogenization approach for the limit analysis of out-of-plane loaded masonry walls[J]. Journal of Structural Engineering, 2006, 32(10): 1650-1663.

[7] POPHN J R B, SCHULZ A E, LU M, STOLARSKI H K, OJARD N J. Influence of transverse loading on the stability of slender unreinforced masonry walls[J]. Engineering Structures, 2008, 30(10): 2830-2839.

[8] BAQI A, BHANDARI N M, TRIKHA D N. Experimental study of pre-stressed masonry flexural elements[J]. J Struct Eng, ASCE, 1999, 125(3): 245-254.

[9] NARAINE K, SHINA S N. Behavior of brick masonry under cyclic compressive loading[J]. J Struct Eng, ASCE, 1989, 115(6): 1432-1445.

[10] RICE J R, RUDNICKI J W. A note on some features of the theory of localization of deformation[J]. Int J Sol Struct, 1980, 16: 597-605.

[11] SMIT R J M. Toughness of heterogeneous polymeric systems: A modeling approach[D]. Netherlands: Eindhoven University of Technology, 1998.

[12] STRVROULAKIS G E. On the static behavior of cracked masonry walls[J]. European Journal of Mechanics, A Solids, 1990, 9(4): 341-358.

[13] MASSART T J, PEERLINGS R H J, GEERS M G D. Structural damage analysis of masonry walls using computational homogenization[J]. International Journal of Damage Mechanics, 2007, 16: 199-226.

[14] WANG Meng-tie. Cracking controlling in engineering structure[M]. Beijing: Chinese Construction Industry Press, 1997. (in Chinese).

[15] SUN Xun-fang, FANG Xiao-shu, GUAN Lai-tai. Materials mechanics[M]. Beijing: Higher Education Press, 1994. (in Chinese).

(Edited by YANG You-ping)

Foundation item: Project(50778067) supported by the National Natural Science Foundation of China

Received date: 2009-03-25; Accepted date: 2009-07-06

Corresponding author: CHEN Da-chuan, Associate professor; Tel:+86-731-88822276; E-mail: 13707311929@139.com