J. Cent. South Univ. Technol. (2010) 17: 612-620
DOI: 10.1007/s11771-010-0530-4 
2D FEM analysis for coupled thermo-hydro-mechanical-migratory processes in near field of hypothetical nuclear waste repository
ZHANG Yu-jun(张玉军)1, ZHANG Wei-qing(张维庆)2
1. Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China;
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: In order to consider the influence of temperature and stress fields on the migration of radioactive nuclide with underground water movement, an elastoplastic model and a 2D FEM code for analysis of coupled thermo-hydro-mechanical (THM) processes in saturated and unsaturated porous media were extended and improved through introducing the percolation and migration equation, so that the code can be used for solving the temperature field, flow field, stress field and nuclide concentration field simultaneously. The states of temperatures, pore pressures and nuclide concentrations in the near field of a hypothetical nuclear waste repository were investigated. The influence of the half life of the radioactive nuclide on the temporal change of nuclide concentration was analyzed considering the thermo-hydro-mechanical-migratory coupling. The results show that, at the boundary of the vitrified waste, the concentration of radioactive nuclide with a half life of 10 a falls after a period of rising, with the maximum value of 0.182 mol/m3 and the minimum value of 0.181 mol/m3 at the end of computation. For a half life of 1 000 a, the concentration of radioactive nuclide always increases with the increase of the time during the computation period; and the maximum value is 1.686 mol/m3 at the end of the computation. Therefore, under the condition of THM coupling, the concentration of radioactive nuclide with a shorter half life will decrease more quickly with water flow; but for the radioactive nuclide with a longer half life, its concentration will keep at a higher level for a longer time in the migration process.
Key words: radioactive nuclide; concentration; thermo-hydro-mechanical-migratory coupling; 2D FEM analysis
1 Introduction
After the stainless steel canisters filled with the high-level radioactive nuclear wastes are placed in a drift at the depth of 500-1 000 m beneath the ground surface, a multi-barrier system composed of vitrified waste, overpack, buffer material and rockmass is formed, which will hinder the leakage and migration of the radioactive nuclides. However, after a very long time, the underground water will penetrate through the buffer by permeation and reach the canister. In a very complicated physical, chemical and mechanical environment, the canister will be damaged finally, so that the radioactive nuclides can diffuse into the surrounding rockmass together with the flow of underground water, and even enter into the biosphere and affect the safety of lives [1-3].
For the interaction among temperature field, stress field, seepage field and solute migration in porous medium, a number of multi-field coupling problems have been studied. For instance, considering the effect on concentration contribution of nuclides due to variable- density groundwater flow, LIANG et al [4] developed a coupled numerical model describing the transportation of radionuclides in matrix-fracture media. Based on the differential control equations of the coupled thermo- hydro-mechanical (THM) processes of dual media, ZHAO et al [5] presented a three-dimensional coupled model of dual media to study the coupled THM processes in fractured rock masses, and a three- dimensional FEM code for analysis of coupled THM processes of dual media was developed. LIU et al [6] established an iterative computation model for the analysis of water flow coupled with stress, adopting the element-by-element (EBE) finite element parallel computation method for numerical simulation. Taking the fracture as a very important permeability channel in the theoretical research on percolation of medium, FENG et al [7] put forward the research method on percolation of more general porous and fractured double-medium. In addition, adopting a double structure approach based on two superimposed domains, OLIVELLA and GENS [8] presented the THM analyses to simulate the drift scale test (DST) performed at Yucca Mountain. Developing a program TOUGH-FLAC in which a double permeability model is used to simulate the rock mass consisting of matrix continuum and fractured continuum, RUTQVIST et al [9] conducted a coupled THM analysis to evaluate the impact of coupled THM processes on the performance of a potential nuclear waste repository at Yucca Mountain. SONNENTHAL et al [10] performed thermo-hydro-chemical simulations using TOUGHREACT code, which includes the coupling among heat, water and vapor flow; aqueous and gaseous species transport; kinetic and equilibrium mineral-water reactions; and feedback of mineral precipitation/dissolution on porosity, permeability and capillary pressure. LIU et al [11] developed and applied a coupled hydrological-mechanical-chemical (HMC) model to explain the spontaneous changes of permeability within the fractures in limestone in in-situ conditions. RUTQVIST et al [12] analyzed air-permeability data by numerical modeling of thermally induced stress and moisture movements and their impact on air permeability in the highly fractured rock. Their analyses showed that changes in air permeability were caused by the combined effects of thermo-mechanically induced stress on fracture aperture and thermo-hydraulically induced changes in fracture moisture content. However, all these researches are limited to hydro-migratory coupling, hydro- mechanical coupling, thermo-hydro-migratory (chemical) coupling, and thermo-hydro-mechanical coupling, the fully coupled thermo-hydro-mechanical-migratory model has not been developed for geological disposal of high-level radioactive nuclear wastes, namely the influence of temperature field and stress field on the migration of radioactive nuclide with underground water has seldom been studied [13-16].
Therefore, in this research, the elastoplastic model for analysis of coupled thermo-hydro-mechanical processes in saturated and unsaturated porous media developed by the author previously will be extended by introducing the percolation-migration equation, thus the model can be also used to describe the transport of radioactive nuclides. The 2D FEM code was improved so that the temperature field, flow field, stress field and nuclide concentration field can be solved simultaneously. The distributions and changes of temperature, pore pressure and nuclide concentration in the near field of a hypothetical nuclear waste repository were investigated. The influence of the half life of radioactive nuclide on the change of nuclide concentration with time was analyzed under the condition of thermo-hydro- mechanical-migratory coupling.
2 Model for thermo-hydro-mechanical- migratory coupling
An isotropic, uniform and continuous porous geological material in the saturated and unsaturated states is assumed in the development of the model considering the effects of the swelling pressure. According to the theories [17-18] concerned, nonisothermal deformable porous media can be simulated utilizing the equilibrium equation and the governing equations of heat and water flow. The main governing equations can be derived and introduced as follows [19-20].
2.1 Incremental stress equilibrium equation
The incremental stress equilibrium equation is
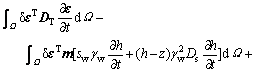
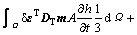
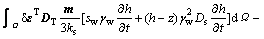
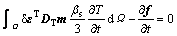(1)
where DT is the tangential matrix, ε is the total strain vector; m is a vector with member equal to unity for the normal stress component and zero for the shear stress component; sw is the degree of saturation of the water phase; γw is the unit weight of the water; h is the total water head; z is the water head above a certain arbitrary stratum; Ds is the moisture capacity and is defined as Ds= ?sw/?pw, and pw is the pore water pressure; A is the computation term for swelling pressure and is defined as
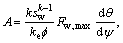k is an empirical constant, ke is the bulk modulus of the porous media, 
is the porosity, Fw,max is the maximum swelling stress which is determined with experiment, θ is the volumetric water content, and 
is the water pressure head; ks is the bulk modulus of the solid;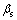 
is the thermal coefficient of solid; T is the temperature; and f is the external force.
According to Ref.[21], the computation formula for the saturation is taken as follows:
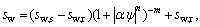
(2)
where m is a constant and is defined as m=1-1/n (0＜ m＜1, n＞1); sw,s and sw,r are the maximum degree of saturation and the minimum degree of saturation, respectively.
2.2 Continuity equation for groundwater
On the basis of the principle of mass balance, the water volume flowing into an object during a time interval ?t is equal to the rate of water accumulated within the object. Assuming that the seepage of water can be expressed with Darcy’s law, after some derivations, the continuity equation for groundwater can be given as follows:
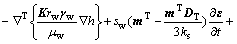
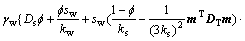
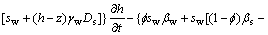
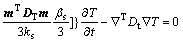(3)
where 
is the Hamilton operator; K is the intrinsic permeability matrix; rw is the relative permeability which is a function of the degree of saturation sw; μw is the dynamic viscosity of water; kw is the bulk modulus of water; βw is the thermal coefficient of water; and Dt is the thermal water diffusivity.
2.3 Conservative equation for heat energy
In accordance with the principle of energy conservation, the rate of heat flow into an object equals the increase of the internal energy within the object. After some derivations, the energy conservation equation is obtained as follows:
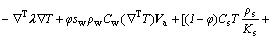
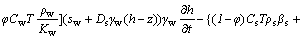
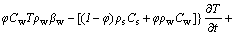
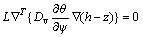(4)
where Cw is the specific heat capacity of water; Cs is the specific heat capacity of solid;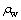 
is the density of water; 
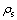is the density of solid; 
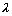is the thermal conductivity matrix of the composite consisting of water and solid; 
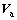is the apparent velocity vector of water; L is the latent heat of water vapor per unit volume; and Dv is the isothermal vapor diffusivity.
2.4 Percolation-migration equation
According to Ref.[22], the percolation-migration equation can be expressed as
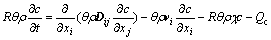(5)
where R is the retardation coefficient and is defined as
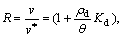v is the apparent velocity of groundwater, v* is the transport velocity of radioactive nuclide, 
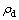is the dry density of geological material, and Kd is the distribution coefficient for saturated porous media; θ is the volumetric water content; Dij is the diffusion tensor; c is the concentration of solute; vi is the apparent velocity of groundwater in direction i; xi and xj are the coordinates in directions i and j, respectively;
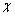is the radioactive decay constant; and Qc is the source term.
The diffusion tensor can be given as
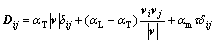(6)
where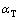 
is the dispersivity in the transversal direction; 
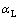is the dispersivity in the longitudinal direction; |v| is the absolute value of the apparent flow velocity;
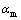is the molecular diffusion coefficient;
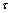is the tortuosity coefficient; and
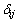is the Kronecker’s delta.
2.5 Yielding functions
Three yielding functions are used in the FEM code. They are: (1) criterion for Mohr-Coulomb model; (2) criterion for modified Cam clay model; and (3) criterion for critical state model.
3 Establishment of FEM solutions
3.1 Discretization in spatial domain
Applying Galerkin’s method, the finite element discretization in spatial domain is carried out for the four governing equations mentioned above and yields
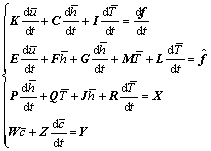(7)
where
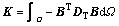
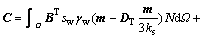
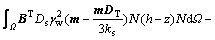
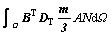
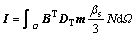
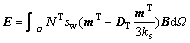
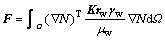
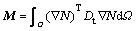
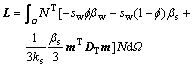
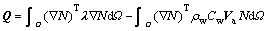
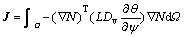
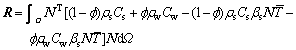
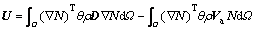
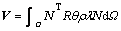
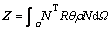
and
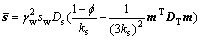
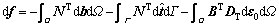
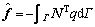
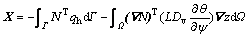
3.2 Temporal discretization
Using the monolithic augmentation approach,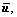 
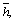
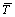and 
are approximated with a linear variation within each time step, ?t, So, Eq.(7) becomes the following form solved with step-by-step method:
?
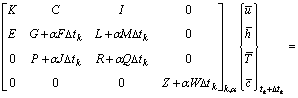
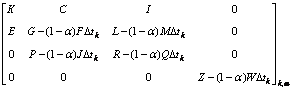(8)
Since the coefficient matrix in Eq.(8) is no longer symmetric, a non-symmetric solver is required.
3.3 Elastoplastic analysis
At every time step, firstly an elastic analysis for the computation domain is made, and the effective stresses of every element are obtained. Then, the effective stresses are substituted into the yield criterion for judgment. If the element enters the plastic state, the relative effective stresses are adjusted iteratively toward the yielding surface; and at the same time, the ‘surplus stresses’ are transformed into the equivalent node forces for the computation at next time step until conversion is reached.
4 Computation example
As shown in Fig.1, it is assumed that a canister filled with the vitrified radioactive nuclear waste is disposed at the depth of 500 m beneath the ground surface, and the unsaturated buffer material is packed around the canister. As an approximate simplification, it is treated to be a plane strain problem. A computation region with a horizontal length of 4 m and a vertical length of 8 m is taken. There are 800 four-nodded elements and 861 nodes in the mesh (Fig.2). The water head at the upper boundary of the computation domain is 100 m, and the rock mass is a saturated medium. After a long time, because of the infiltration of groundwater from the surrounding rock mass, the buffer material reaches the saturated state and unfortunately the canister is damaged by corrosion so that the radioactive nuclides begin to leak out into the near field with the constant concentration and rate from the canister. The time when the nuclides begin to leak out is taken as the starting point of the computation. Let the initial temperature of the region be 20℃ at the beginning (uniform distribution). The vitrified waste is the source term with a diffusive mass flux Qc/ρw=7.0×10-4 mol/(m3·s), and it radiates heat continuously with a power of 500 W. The fixed temperature of 20 ℃ and the fixed hydrostatic total heads are applied at the upper and bottom boundaries. The side boundaries are adiabatic and impermeable. The stress redistribution and the head change duo to excavation are not considered, and the thermal water diffusivity, Dt, as well as the isothermal vapor diffusivity, Dv, is not taken into account. The main physico-mechanical parameters of the rock mass, the vitrified waste and the buffer material are presented in Table 1.
Referring to Ref.[22], the parameters used in the computation concerned with the percolation-migration of some
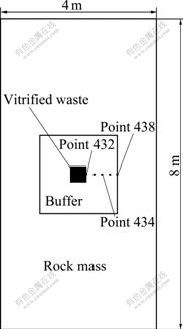
Fig.1 Computation region
Fig.2 Finite element mesh
kinds of nuclide in the near field are supposed as follows: the tortuosity coefficient τ=0.4, the dispersivity in the longitudinal direction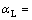 
1.0 m, the dispersivity in the transversal direction 
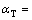0.1 m, the molecular diffusion coefficient
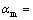20.0×10-10 m2/s, the distribution coefficient kd=80.1 mL/g (for buffer) and 8.3 mL/g (for rockmass), and the radioactive decay constant λ=ln 2/Thalf, where Thalf is the half life of the nuclide which is taken sequentially as 10, 100 and 1 000 a in the computation.
The time simulated in the computation is 1 150 d (during this period the power of the vitrified waste is unchanged).
Under the condition of thermo-hydro-mechanical- migratory coupling, the temperature contours in the near field at 1 000 d are shown in Fig.3(a). It can be seen that the temperature contours are symmetrically distributed around the vitrified waste basically. The temperature variations with the time at some special points in Fig.1 are plotted in Fig.3(b). It can be seen that temperature changes with time almost linearly. When a computation stops, the temperatures reach 23.48, 23.37, 23.31, 23.28 and 23.28 ℃ for points of 432, 433, 434, 435 and 436, respectively. Because of the thermal effects, the flow state in the near field also produces some changes, and the water head contours are presented in Fig.4. It can be seen that the water heads increase due to the effect of temperature gradient, but they rise more quickly at about 500 d of the early stages and then the rising rates slow down. The total heads versus time at some special points in Fig.1 are plotted in Fig.4(b). At the end of the computation, the water heads reach 106.1, 105.3, 104.5, 103.4 and 103.2 m for points of 432, 433, 434, 435 and 436, respectively.
When the decay constant is determined using the half life of 10 a, the contours of nuclide concentration in the near field at 150 d are illustrated in Fig.5(a), which are primarily concentric circles around the vitrified waste. The relationships between concentration and time at some special points in Fig.1 are plotted in Fig.5(b). It can be seen that, because the half life is shorter, the nuclide concentrations of these points increase initially; but the rates of increasing decrease with the time; and after some periods of time, the nuclide concentrations begin to drop. For instance, the nuclide concentration at point 432 reaches the maximum value of 0.182 mol/m3 at 870 d; yet at 1 150 d the concentration reduces to 0.181 mol/m3. The nuclide concentration at point 433 reaches the maximum value of 0.016 1 mol/m3 at 100 d; but at 310 d the concentration reduces to 0 mol/m3.
Table 1 Main computation parameters of medium
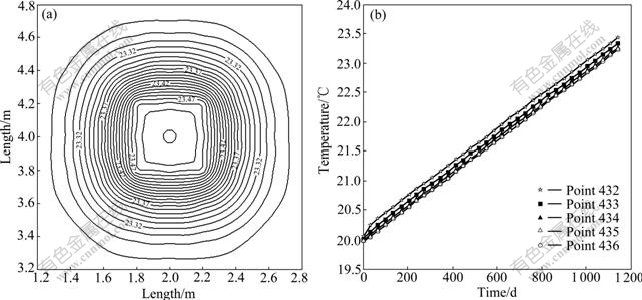
Fig.3 Temperature (℃) contours at 1 000 d around waste (a) and temperature vs time plots at different nodes (b)
Fig.4 Water head (m) contours at 1 000 d around waste (a) and water head vs time plots at different nodes (b)
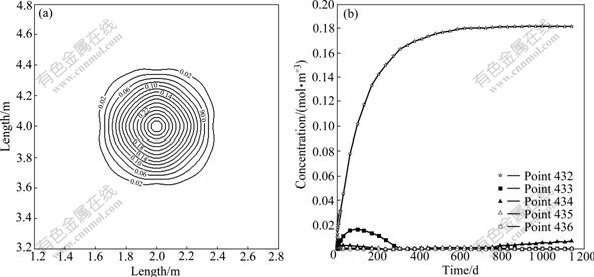
Fig.5 Concentration (mol/m3) contours of nuclide at 150 d around waste (a) and concentration vs time plots at different nodes for nuclide (b) with half life of 10 a
When the decay constant is determined using the half life of 100 a, the contours of nuclide concentration in the near field at 1 000 d are shown in Fig.6(a). The relationships between concentration and time at some special points in Fig.1 are plotted in Fig.6(b). From these figures, it can be known that, because the half life is longer, the increasing rate of the nuclide concentration dropping with the time is smaller than that in the first case. For example, the nuclide concentration at point 432 rises until the end of the computation and reaches the maximum value of 1.099 mol/m3. The nuclide concentration at point 433 reaches the maximum value of 0.120 mol/m3 at 670 d; but at 1 150 d the concentration drops to 0.081 mol/m3.
When the decay constant is determined using the half life of 1 000 a, the contours of nuclide concentration in the near field at 1 000 d are shown in Fig.7(a), and the relationship between concentration and time at some special points in Fig.1 are plotted in Fig.7(b). From these figures, it can be seen that, since the half life is longer than that in the second case, the increasing rate of the nuclide concentration dropping with the time is smaller than that in the second case. For instance, the nuclide concentrations at points 432 and 433 reach 1.686 mol/m3 and 0.295 1 mol/m3 at 1 150 d, respectively, and the nuclide concentration in every point increases monotonously during the computation period. The phenomena described above tell that, if the nuclear waste disposed leaks out, for the radioactive nuclides with the shorter half lives, the nuclide concentrations in groundwater will decrease more quickly, which may be harmless to the biosphere. However, for the radioactive nuclides with the very long half lives, the nuclide concentrations in groundwater will keep at higher level for a very long time, which may endanger the ecological environment.
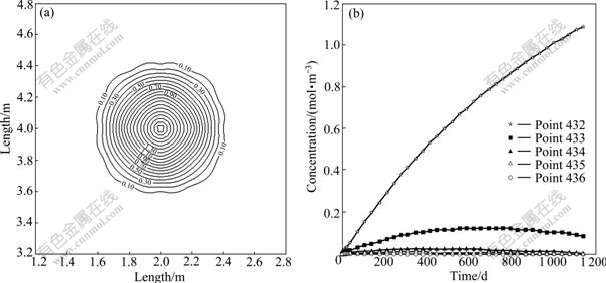
Fig.6 Concentration (mol/m3) contours of nuclide at 1 000 d around waste (a) and concentrations vs time plots at different nodes for nuclide (b) with half life of 100 a
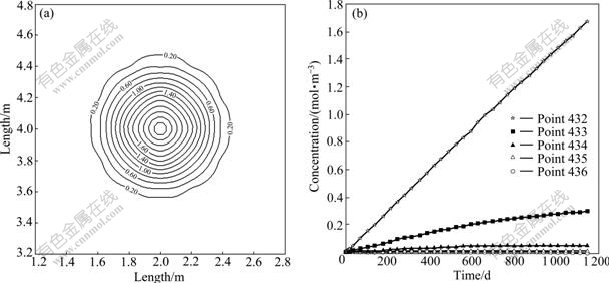
Fig.7 Concentration (mol/m3) contours of nuclide at 1 000 d around waste (a) and concentration vs time plots at different nodes for nuclide (b) with half life of 1 000 a
As mentioned above, the coupled thermo-hydro- mechanical-migratory model and the corresponding FEM code can be used for solving the temperature field, flow field, stress field and nuclide concentration field simultaneously, and the influence of half life of radioactive nuclide on the change of nuclide concentration with time is mainly analyzed.
5 Conclusions
(1) The promoting factors for migration of the radioactive nuclides in geological material are the groundwater convection, molecular diffusion and mechanical dispersion (representative parameters are flow velocity and diffusion coefficient (tensor)); and the hindering factors are the adsorption and nuclide decay (representative parameters are retardation coefficient and decay constant). Among them, the convection, diffusion and retardation are related to the movement of groundwater closely. Under the special conditions of the geological disposal of nuclear waste, the groundwater movement, the stress field and the temperature field in rock mass influence each other and act simultaneously.
(2) In order to accurately simulate the migration of radioactive nuclides, it is necessary to analyze the temperature field, the flow field, the stress field and the nuclide concentration field with a coupled method. For this reason, the momentum equilibrium equation, the continuity equation for water, the heat energy balance equation, the percolation-migration equation and the elastoplastic matrix are established or introduced.
(3) Using the Galerkin’s method, all the governing equations are discretized in the spatial and temporal domains, respectively, leading to the development of a two-dimensional FEM code for elastoplastic analysis of coupled thermo-hydro-mechanical-migratory processes in saturated and unsaturated porous media.
(4) Through a numerical computation of a hypothetical nuclear waste repository, the distributions and changes of temperatures, pore pressures and concentrations of nuclides with different half lives in the near field are investigated. The computed results show that, when the other conditions are the same, the concentration of radioactive nuclide with a shorter half life in groundwater will decrease more quickly in the transport process; and for the radioactive nuclide with a longer half life, the concentration will keep at a higher level in the transport process for a longer period. This conclusion is identified with the practical case qualitatively.
References
[1] CHIJIMATSU M, NGUYEN T S, JING L, JONGE J, KOHLMEIER M, MILLARD A, REJEB A, RUTQVIST J, SOULEY M, SUGITA Y. Numerical study of the THM effects on the near-field safty of a hopothetical nuclear waste repository—BMT1 of the DECOVALEX III Project. Part 1: Conceptualization and characterization of the problems and summary of results [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 720-730.
[2] MILLARD A, REJEB A, CHIJIMATSU M, JING L, JONGE J, KOHLMEIER M, NGUYEN T S, RUTQVIST J, SOULEY M, SUGITA Y. Numerical study of the THM effects on the near-field safty of a hopothetical nuclear waste repository—BMT1 of the DECOVALEX III Project. Part 2: Effects of THM coupling in continuous and homogeneous rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 731-744.
[3] RUTQVIST J, CHIJIMATSU M, JING L, MILLARD A, NGUYEN T S, REJEB A, SUGITA Y, TSANG C F. Numerical study of the THM effects on the near-field safety of a hopothetical nuclear waste repository—BMT1 of the DECOVALEX III Project. Part 3: Effects of THM coupling in sparsely fractured rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 745-755.
[4] LIANG Bing, LIU Lei, XUE Qiang, SUN Wei-ji. Study on numerical simulation of nuclides leakage for groundwater pollution [J]. Journal of System Simulation, 2007, 19(2): 261-311. (in Chinese)
[5] ZHAO Yan-lin, CAO Pong, ZHAO Yang-sheng, LIN hang, WANG Yi-xian. Dual media model for thermo-hydro-mechanical coupling and 3D numerical simulation [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S2): 4024-4031. (in Chinese)
[6] LIU Yao-ru, YANG Qiang, HUANG Yan-song, LI Xiao-qin. Parallel numerical analysis of coupled fluid flow and stress based on dual porosity media model [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 705-711. (in Chinese)
[7] FENG Zeng-chao, ZHAO Yang-sheng, L? Zhao-xing. Study on percolation law of 2D porous and fractured double-medium [J]. Acta Physica Sinica, 2007, 56(5): 2796-2801. (in Chinese)
[8] OLIVELLA S, GENS A. Double structure THM analyses of a heating test in a fractured tuff incorporating intrinsic permeability variations [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 667-679.
[9] RUTQVIST J, BARR D, DATTA R, GENS A, MILLARD A, OLIVELLA S, TSANG C F, TSANG Y. Coupled thermal- hydrological-mechanical analyses of the Yucca Mountain Drift Scale Test—Comparison of field measurements to predictions of four different numerical models [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 680-697.
[10] SONNENTHAL E, ITO A, SPYCHER N, YUI M, APPS J, SUGITA Y, CONRAD M, KAWAKAMI S. Approaches to modeling coupled thermal, hydrological, and chemical processes in the drift scale heater test at Yucca Mountain [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 698-719.
[11] LIU J, SHENG J, POLAK A, ELSWORTH D, YASUHARA H, GRADER A. A fully-coupled hydrological-mechanical-chemical model for fracture sealing and preferential opening [J].International Journal of Rock Mechanics and Mining Sciences, 2006, 43(1): 23- 36.
[12] RUTQVIST J, FREIFELD B, MIN K B, ELSWORTH D, TSANG Y. Analysis of thermally induced changes in fractured rock permeability during 8 years of heating and cooling at the Yucca Mountain Drift Scale Test [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(8): 1373-1389.
[13] ZHU W C, BRUHNS O T. Simulating excavation damaged zone around a circular opening under hydromechanical conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 815-830.
[14] IVARS D M. Water inflow into excavations in fractured rock—A three-dimensional hydro-mechanical numerical study [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(5): 705-725.
[15] MIN K B, RUTQVIST J, TSANG C F, JING L. Thermally induced mechanical and permeability changes around a nuclear waste reposity—A far-field study based on equivalent properties determined by a discrete approach [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 765-780.
[16] YUAN S C, HARRISON J P. Development of a hydro-mechanical local degradation approach and its application to modelling fluid flow during progressive fracturing of heterogeneous rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(7/8): 961-984.
[17] LEIWS R W, SCHREFLER B A. The finite element method in the deformation and consolidation of porous media [M]. New York: John Wiley, 1987.
[18] CHIJIMATSU M, FUJITA T, KURIKAMI H, ITO A, SUGITA Y. Subtask BMT1-B: Implication of THM coupling on the near-field of a nuclear waste repository in a homogeneous rock mass [R]. DECOVALES III-Task3-Bench Mark Test 1(BMT1)- 2002: 1-43.
[19] ZHANG Yu-jun. Coupled thermo-hydro-mechanical model and 2D FEM analysis for FEBEX in situ test [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 313-318. (in Chinese)
[20] ZHANG Yu-jun. Coupled thermo-hydro-mechanical model and relative numerical analysis for near field of conceptual nuclear waste repository [J]. Rock and Soil Mechanics, 2007, 28(1): 17-22. (in Chinese)
[21] KURIKAMI H. Study on modeling for coupled thermo-hydro- mechanical phenomena in rock mass [D]. Kyoto: Kyoto University, 2003. (in Japanese)
[22] NISHIGAKI M. Density dependent transport analysis saturated- unsaturated porous media—3. Dimensional Eulerian Lagrangian method [R]. Okayama University, 2001.
Foundation item: Project(2010CB732101) supported by the National Basic Research Program of China; Project(SKLQ 008) supported by the Research Fund of State Key Laboratory of Geomechanics and Geotechnical Engineering of China
Received date: 2009-07-31; Accepted date: 2010-01-23
Corresponding author: ZHANG Yu-jun, PhD; Tel: +86-27-87198482; E-mail: yjzhang@whrsm.ac.cn
(Edited by YANG Bing)
