Simulation of interphase boundary of Ni75AlxV25-x alloys using microscopic phase-field method

LI Yong-sheng(李永胜), CHEN Zheng(陈 铮), LU Yan-li(卢艳丽),WANG Yong-xin(王永欣)

Department of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 22 April 2005; accepted 26 August 2005

Abstract: The evolution of ordered interphase boundary (IPB) of Ni₇₅Al_xV_25-x alloys was simulated using the microscopic phase-field method. Based on the atomic occupation probability figure on 2D and order parameters, it was found that the IPB formed by different directions ofθ phase has great effect on the precipitation of phase. The  phase precipitated at the IPB that is formed by 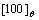 direction where the  plane is opposite, and then grows up and the shape is strap at final. The IPB structure between phase andθ phase is the same. There is no  phase precipitate at the IPB where the  and  planes are opposite, the ordered IPB is dissolved into disordered area. There is  phase precipitation at the IPB formed by the 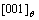 and 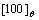 directions, and the IPB structure is different between  phase and the different directions ofθ phase. 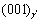The IPB where  and  plane opposite does not migrate during the  phase growth, and  phase grows along 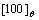direction.

Key words: Ni₇₅Al_xV_25-x alloy; microscopic phase-field method; ordered interphase boundary; simulation

1  Introduction

The phase transformation is affected on great degree by the interphase boundary(IPB) structure and migration, the component, structure and migration cha- racteristic of IPB have been of scientific interest for many years. With the methods of scanning tunneling microscopy(STM), high-resolution transmission electron microscopy(HRTEM) and atom probe-field ion microscopy(AP-FIM), the studies of IPB on atomic-scale have made great progress[1—3]. But the study about migration behavior on atomic-scale is still less. The computer simulation technique could obtain the microscopic message of IPB during phase transformation[4—6]. It has important theoretic value to investigate the IPB microscopic structure on improving the alloy capability and optimize the alloy system.

Based on the Ginzburg-Landau or Onsage dynamic equation, Khachaturyan[7] found the microscopic phase-field dynamic model. The simulation on atomic-scale for the diffusion phase transformation of crystal materials was realized. This model has been successfully used in the precipitation process of binary and ternary alloy system[8—10]. With the improved eular method, the equation was solved in reciprocal space through Fourier transformation. In this paper, the Ni₇₅Al_xV_25-x alloys were studied, which undergo the eutectoid reaction at 1 281 K, and precipitate two ordered phases (Ni₃Al, L1₂) and (Ni₃V, D0₂₂)[11—13]. The nickel-based intermetallics Ni₃X which have topological close packed structure, have their own characteristic properties as high temperature structure and chemical materials. In this paper, the IPB structure was focused on that were formed by  phase and the migration direction of  phase precipitated at the IPB, and the atom replacing process during two phases transform.

2 Microscopic phase-field model

Microscopic phase-field dynamic equation was based on the Ginzburg-Landua equation, the atomic structure and alloy morphological were described by a single-site occupation probability function x(r, t), which was the probability that a given lattice site r was occupied by an atom at time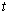. The change rate of these probabilities are linearly proportional to the thermodynamics driving force:

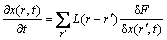                 (1)

where  F is the function of free energy of, is the symmetry matrix of microscopic kinetic related to the probability of an atom jump from site r to r' per unit of time.

The ternary system microscopic was developed by CHEN[14]. For ternary system, the atomic configurations and morphologies are described by single-site occupation probability functions P_A(r, t), P_B(r, t) and P_C(r, t), which represent the probability of finding an A, B or C atom at a given lattice siteand at a given time step t. P_A(r, t)+P_B(r, t)+P_C(r, t)=1, only two equations are independent at each lattice site. In order to describe the initial thermal fluctuations such as the nucleation, a random noise item to the right-hand side of the equation was added, then the microscopic Langevein equation of ternary system was obtained:

      (2)

where 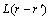 is a constant related to the exchange probabilities of a pair of atoms, αand β, at lattice site r and  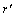per unit time; α,β(A, B or C).  is assumed to be Gaussian-distributed with the average value of zero, which is uncorrelated with space and time. It obeys the so-called fluctuation dissipation theory[15], F is the total free energy of the system, Based on mean-field approximation , F is given by the following equation:

     (3)

where   is the interaction energy between αandβat the lattice site of 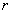and .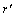

For there are three kinds of atoms migrating and arranging in ternary system, the fourth–nearest neighbor interchange energies are adopted which can describe the free energy more  accurate. If  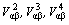 are the first, second, and the ith-nearst neighbor effective interchange interaction energies, then

 　       (4)

The relation between the reciprocal lattice vectors and 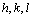 are

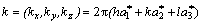              (5)

where 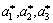 are the unit reciprocal lattice vectors of the fcc lattice along [100], [010] and [001] directions.

3 Results and discussion

The simulated pictures are depicted with different grey levels, if the occupation probability of vanadium is 1.0, then that site is white, so  phase is white, if occupation probability of nickel is 1.0, then that site is black, so the matrix is black, the color of  phase is grey. The ordered phases structures are shown in Fig.1. In order to depict the IPB relations, the different atomic planes in the projection figure of D0₂₂ were prescribed. As shown in Fig.1(b), if all the sites are nickel atoms in a plane of D0₂₂, then this plane is (002), if nickel and vanadium atoms both exist in the plane, the plane is (001). The simulation is performed with 256×256 mesh points, a periodical boundary condition is imposed along both dimensions. The initial condition for the simulation is a homogeneous disordered supersaturated solid solution. The time increment 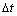is 0.000 2, and the thermal fluctuations are removed after nucleation, then the system chooses dynamic path automatically.

3.1 Interphase boundary formed by [100]_θ direction

Fig.2 shows the microscopic structure evolution of Ni₇₅Al_4.3V_20.7 alloy during precipitation at 1 185 K. Fig.2(a) shows the state at t=36 000, the θ phase has  precipitated and some  phases have formed ordered IPB. The IPB that are labeled with arrow A in Fig.2(a) is formed by the [100]_θ direction. The atomic structure schematic diagram is shown in Fig.3(a). The IPB is narrower, the distance is about 2－3 atoms, which has the crystal lattice characteristic of D0₂₂, so the IPB is continuous in the schematic diagram, although the occupation probability is lower at there.  The  plane is opposite at the IPB, so the orientation of ordered phases and atomic plane matching are same for this state. 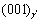As the precipitation progress, the Al atoms begin to migrate to the IPB and form  phase, where the  plane is opposite to , as shown in Fig.2(b). As the Al atoms precipitate continuously, the V atoms at one  plane of D0₂₂ are replaced by Al atoms, the Ni and V atoms at another  plane of D0₂₂  are replaced by Al and Ni atoms respectively, but the  plane does not change, then the transformation of two phases is finished. 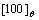The  phase grows along the direction, the  phase IPB migrates to its interior, so  phase continuously decreases, as shown in Figs.2(b)－(d). There form the IPB between two phases of  and , and the IPB structure at two sides of  are the same, the magnified atomic figure for the IPB is shown in Fig.2(a^′). The  phase grows up along the IPB, so they are distributed among  phases and have the shape of strap (Fig.2(d)).

Fig.1 Ordered phases structures: (a) D0₂₂  crystal structure;  (b) Projection of D0₂₂; (c) L1₂ crystal structure; (d) Projection of L1₂

Fig.2 Microstructure evolution of Ni₇₅Al_4.3V_20.7 alloy at 1 185 K: (a) t=3 600; (b) t=45 000; (c) t=60 000; (d) t=100 000; (a^′)－(d^′) Magnified atomic structure figure for arrows A, B, C and D in (d)

The other case is that the opposite atomic planes are  and  at the IPB formed by 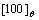 direction, which are labeled with arrow B in Fig.2(a). The atomic structure schematic diagram is shown in Fig.3(b). There is not  phase precipitate at this kind of IPB, as shown in Figs.2(b)-(d). As the precipitation process progress, the ordered IPB begins to dissolve and becomes wider, there forms the order-disorder area at last (Fig.2(b^′)). The reason for this is that the  phase is nonstoichiometric at initial, as the precipitation process progress, the V atoms migrate from the IPB to the interior, therefore the  phase attains the stoichiometric. Fig.4 shows the order parameter of  phase. The composition order parameter (Fig.4(b)) rises slowly and the width is invariable, which has the characteristics of spinodal decomposition. When the composition order parameter attains the maximum, it becomes narrower. This corresponds to the disorder of the IPB. The long range order (LRO) parameter has the same variety tendency (Fig.4(a)). So the ordered IPB is disordered gradually by means of the spinodal decomposition of  phase. However, the  phase does not precipitate at the IPB, the Ni atoms migrate to the IPB. It can be seen that the opposite relationship of atomic planes at the IPB is disadvantageous for  phase precipitate. If γ' phase precipitates at the IPB, and grows along  the 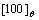 direction, besides the V atoms on (100)_θ planes need to exchange with Ni atoms, Ni atoms on the  plane need to exchange with Al atoms in order to realize the L1₂ structure. This needs to overcome more potential for atoms jump, so the  phase does not precipitate.

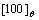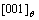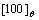Fig.3 Atomic structure schematic diagrams of  phase IPB: (a), (b)  direction; (c)  and  directions;      (d)  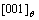direction

In order to show the evolution of the IPB, the order parameter of  phase and the disorder area between the  phases are calculated. Fig.5(a) shows the LRO of  phase that are labeled with arrow A in Fig.2(d). The LRO has the cupped value at t=24 000 as shown in Fig.5(a). This shows that the  phase IPB is formed. At t=35 000, the curve begins to rise and takes on the distribution of higher at middle and lower at side, which shows that the  phase begins to precipitate at the IPB, and the new heterophase IPB forms between the two phases. As the precipitation process progress, the LRO reaches the maximum and the width does not change, this process corresponds to the  nucleation and growth of  phase, the  phase changes from nonstoichiometric to stoichio- metric. Then the LRO becomes wider, which corres- ponds to the farther growth of  phase. Compared with the order parameter of  phase, it can be seen that the variety of two phases order parameter is opposite at later stage. This demonstrates that  phase grows to the  phase, which makes the  phase become smaller continuously.

It is not the same with the  phase IPB where  phase precipitates. Fig.5(b) shows the order parameter of the disorder area between the  phases that are labeled with arrow B in Fig.2(d). It can be seen that the order parameters have the tendency of degression. At t＝18 000，the LRO is the minimum, then it begins to rise slowly and the shape is concavity. At t＝23 000, the LRO does not rise, the curve is narrower, this shows that the  phase encounters and form the order IPB. Then the order parameter falls  continuously and becomes wider until attains the minimum. This process corresponds to the disorder of the  phase IPB.

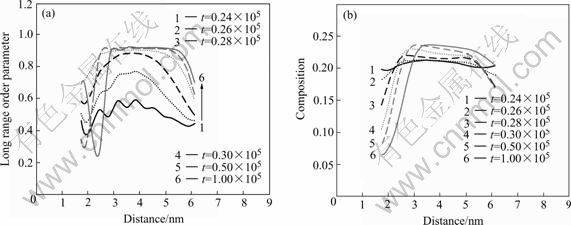
Fig.4 Order parameter curves of  phase at different time steps: (a) Long range order parameter; (b) Composition parameter

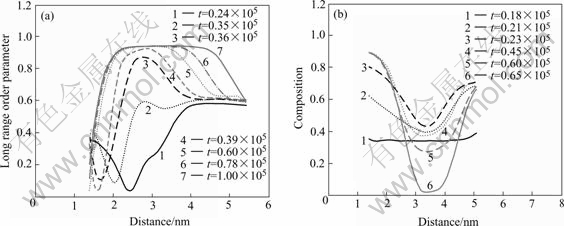
Fig.5 Long range order parameter curves of γ' phase(a) and composition parameter of IPB of  phase(b) at different time steps

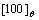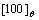It can be concluded from the discussion mentioned above that there is no  phase precipitates at the IPB formed by  direction and the and  planes are opposite, the ordered IPB is dissolved into disordered area. The  phase precipitates at the IPB formed by  direction where the  plane are opposite, and then grows up. From the analogical structure of the  and  phases, it can be known that the same atom planes opposite offer the advantage of two phases transformation, the Ni atoms of  don’t need to migrate during two phases transformation. If the  and  planes are opposite, the V and Ni atoms on the two planes all need to exchange with Al atoms, the jump potential of atoms is greater than that of the first transformation quomodo. So this kind of IPB is disadvantage for two phases transformation.

3.2 Interphase boundary formed by [001]_θ and  [100] _θ  directions

The IPB labeled with arrow C in Fig.2(a) is formed by the 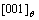and 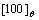 directions，the atomic structure schematic diagram is shown in Fig.3(c). At t＝45 000,  phase has precipitated. It can be seen from Figs.2(b)－(d) that the  phase grows along the 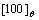 direction, the IPB formed by  phase and  phase at initial keeps fixed，where the (001) and  planes are opposite. It is labeled with arrow A in Fig.2(c^′), in where the atom occupation probability reaches the equilibrium value. The IPB labeled with arrow B in Fig.2(c^′) is moveable during two phases transformation. 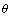There form two different heterophase IPBs between  and  phases.

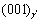At the direction of  phase growth, the  plane is opposite to the two  planes respectively, namely the planes containing Al atoms are opposite to that of V atoms, the remnant planes only contain Ni atoms. During the transformation of two phases, the Al atoms replace the V atoms of one  plane, and the Ni atoms replace V atoms of the other  plane and Al atoms replace the Ni atoms of this plane, the  planes do not change. Compared with the 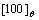 direction where  planes are opposite, it can be known that the precipitation quomodo and growth direction are the same for the two kinds of IPB, although the structures are different. The atom jumps along the planes and directions that have the minimum potential.

In the simulation, the  phase don’t precipitate at the IPB formed by 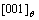 direction, as shown in Figs.2(a) and (d) labeled with arrow D, the atomic structure schematic diagram is shown in Fig.3(d). This kind of IPB has the same characteristics as that are formed by  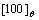direction where the  and  planes are opposite. So they are the fixed IPBs. Fig.2(d^′) shows the magnified atomic figure of final state.

4 Conclusions

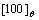1) The  phase precipitates at the IPB formed by  direction where the  planes are opposite, and distribute between  phases and have the shape of strap at final. The IPB structure between  phase and  phase is the same. There is no  phase precipitated at the IPB where the  and  planes are opposite, the ordered IPB dissolves into disordered area.

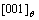2) There is  phase precipitation at the IPB formed by the  and 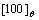 directions, and the IPB structure is different between  phase and the different directions of 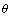 phases. The IPB where  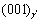and  planes are opposite does not migrate during the  phase growing, and  phase grows along 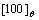 direction.

3) Through the spinodal decomposition, the  phase transforms from nonstoichiometric to stoichiometric, and the IPB formed by θ phase either precipitates the  phase or dissolves into disordered area.

4) The IPB formed by 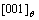direction is fixed during the precipitation process, where no  phase precipitates.

References

[1] PING D H, LI D X, HUANG J Y, HE L L. Interphase Boundary Research of Advanced Materials: Interphase Boundary Structure and Characteristics of Materials[M]. Beijing: Science Press, 1999. 64－92. (in Chinese)

[2] Sakata T, Yasuda H Y, Umakoshi Y. Effect of coherency on interphase boundary sliding in NiAl(β) bicrystals with film-like Ni₃Al() precipitate along boundary[J]. Scripta Materialia, 2003, 48: 749－753.

[3] Jezierska E, Morniroli J P. Antiphase boundaries in Ni₃Al ordered intermetallic-application of the CBED method[J].Materials Chemistry and Physics, 2003, 81: 443－447.

[4] Bursik J. Monte Carlo simulation of ordering in fcc-based stoichiometric A₃B and AB solid solutions[J]. Materials Science and Engineering A, 2002, 324: 16－22.

[5] Bishop C M, Carter W C. Relating atomistic grain boundary simulation results to the phase-field model[J]. Computational Materials Science, 2002, 25: 378－386.

[6] ZHOU Long-guang, HE Lian-long, YE Heng-qiang. Computer simulations on grain boundary in TiAl and its comparison with experimental observations[J]. Journal of Chinese Electron Microscopy Society, 2002, 21(3): 240－246.

[7] Khachaturyan A G. Theory of Structural Transformation in Solids[M]. New York: Wiley, 1983. 129.

[8] WANG Yong-xin, CHEN Zheng, LIU Bing, MA Liang, TANG Li-ying, ZHAO Yu-hong. Computer simulation on precipitation mechanism of phase in early stage in external energy field[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(2): 255－262. (in Chinese)

[9] LI Yong-sheng, CHEN Zheng, WANG Yong-xin, LU Yan-yi. Computer simulation of and phases precipitation of Ni-Al-V alloy using microscopic phase-field method[J]. Trans Nonferrous Met Soc China, 2005, 15(1): 57－63.

[10] Poduri R, Chen L Q. Computer simulation of morphological evolution and coarsening kinetics of precipitations in Al-Li alloys[J]. Acta Mater, 1998, 46(11): 3915－3928.

[11] Zapolsky H, Pareige C, Marteau L, BLAVETTE D. Atom probe analyses and numerical calculation of ternary phase diagram in Ni-Al-V system[J]. Calphad, 2001, 25(1): 125－134.

[12] Pareige C, Blavette D. Simulation of the FCC→FCC+L1₂+DO₂₂ Kinetic Reaction[J]. Scripta Mater, 2001, 44: 243－247.

[13] Marteau L, Pareige C, Blavette D. Imaging the three orientation variants of the D0₂₂ phase by 3D atom prob microscopic[J]. Journal of Microscopy, 2001, 204(3):247－251.

[14] Chen L Q. A computer simulation technique for spinodal decomposition and ordering in ternary systems[J]. Scripta Metall Mater, 1993, 29: 683－688.

[15] Lifshitz E M, Pitaevski L P. Statistical Physics[M]. Oxford: Pergamon Press, 1980. 363.

Foundation item: Project (50071046) supported by the National Natural Science Foundation of China; Project (2002AA331051)supported by the National Hi-Tech Research and Development Program of China

Corresponding author: LI Yong-sheng; Tel: +86-29-88474095; E-mail: ysli@mail.nwpu.edu.cn

(Edited by LI Xiang-qun)