J. Cent. South Univ. Technol. (2011) 18: 1178-1183

DOI: 10.1007/s11771-011-0820-5

Consensus tracking protocol and formation control of multi-agent systems with switching topology

NIAN Xiao-hong(年晓红), SU Sai-jun(苏赛军), PAN Huan(潘欢)

School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: Consensus tracking control problems for single-integrator dynamics of multi-agent systems with switching topology are investigated. In order to design effective consensus tracking protocols for a more general class of networks, which are aimed at ensuring that the concerned states of agents converge to a constant or time-varying reference state, new consensus tracking protocols with a constant and time-varying reference state are proposed, respectively. Particularly, by contrast with spanning tree, an improved condition of switching interaction topology is presented. And then, convergence analysis of two consensus tracking protocols is provided by Lyapunov stability theory. Moreover, consensus tracking protocol with a time-varying reference state is extended to achieve the formation control. By introducing formation structure set, each agent can gain its individual desired trajectory. Finally, several simulations are worked out to illustrate the effectiveness of theoretical results. The test results show that the states of agents can converge to a desired constant or time-varying reference state. In addition, by selecting appropriate structure set, agents can maintain the expected formation under random switching interaction topologies.

Key words: multi-agent system; consensus protocols; formation control; switching topology

1 Introduction

Motivated by diverse research topics, such as coordination, flocking and formation of groups of mobile autonomous agents, the consensus problem for multi-agent systems has attracted more and more attention in recent years. Consensus protocols are distributed control policies based on local information that allows the coordination of multi-agent systems. Coordination of agents is an important task in several applications including cooperative control of unmanned air vehicles, formation flight control [1-5], distributed sensor networks [6] and congestion/flow control in communication networks [7].

In the past decade, consensus problem has been investigated from different perspectives and with different assumptions. The work in Ref.[8], as one of the pioneer work in this area, proposed linear and nonlinear consensus protocols for a network of dynamic agents with integrator dynamics and undirected information flow graphs. And it was further assumed that the directed topology is balanced and strongly connected. In Ref.[9], REN and BEARD extended the results of Refs.[8, 10] and presented some improved conditions for state agreement under dynamically changing directed topology, which must have a directed spanning tree. Existing consensus protocols in Refs.[10-15] needed to change controllers time by time with switching topologies. Moreover, tools from algebraic graph theory were used to prove the formation stability [10-11]. Graph Laplacians and their spectral properties play a crucial role in convergence analysis of consensus and alignment algorithms [8, 10-11, 16]. However, the stability of graph Laplacians is a kind of critical stability condition, which is not available in application. Finally, the consensus equilibrium [10-11, 17-18] is a weighted average of the initial information states of all agents, hence it is a constant. This constant consensus equilibrium, which depends on the interaction topology, might be a priori unknown. The assumption of constant consensus equilibrium might not be appropriate when the information state evolves over time of each agent, as that occurring in formation control problems. To guarantee the formation to track a time-varying reference state, current approach proposed by REN relies on the assumption that all switching interaction topologies have a directed spanning tree [19-22], which, generally speaking, cannot be satisfied in application with the random switching.

To overcome these difficulties, we follow the work in Refs.[20-21] and consider some new consensus tracking protocols for a more general class of networks. Firstly, consensus tracking protocols with a constant and time-varying reference state are proposed. Then, asymptotic convergence analysis of consensus problems is provided by introducing a Lyapunov function. In this case, consensus tracking protocol ensures that the information states converge to a desired, or reference states. Finally, we experimentally implement a consensus tracking protocol on a formation control problem in the case of dynamically switching topologies. According to the formation structure set, each agent can track its individual desired trajectory. To verify the effectiveness of theoretical results, simulations are performed.

2 Problem formulation

Let G=(V, ε, A) be a directed generalized graph with the set of nodes V={v₁, …, v_n}, set of edges εv×v, and a weighted adjacency matrix A=[a_ij]R^n×n with non-negative adjacency elements a_ij, where a_ij>0 means that node i receives information from node j. The node indexes belong to a finite index set ⊥={1, 2, …, n}. An edge of G is denoted by e_ij=(v_i, v_j), e_ijεa_ij>0. The set of neighbors of node v_i is denoted by N_i={v_jV|(v_i, v_j) ε}. Particularly, if node v­_iV has a self-feedback controller, then a_ii>0. The union of directed graph G(t) with constant vertex set across time interval [t⁰, t⁰+T] is a directed graph with the same vertex set as G(t) and the

edge set  The union of directed graph G(t) on the time set {t₀, t₁, …, t_k, …} is a directed graph with constant vertex set as  and the edge set  The in-degree and out-degree of node v_i are defined as

In a multi-agent system, each agent can be considered as a node in a generalized graph, and the information flow between two agents can be regarded as a directed path between the nodes. Thus, the interconnection topology in a multi-agent system can be described by a directed graph G=(V, ε, A). Let x_i denote the value of node v_i. We refer to G_x=(G, x) with x=(x₁, x₂, …, x_n)^T as a network (or algebraic graph) with value x and topology G. The value of a node might represent various physical quantities such as attitude, position, temperature, and voltage.

3 Consensus tracking protocols

Suppose that n agents in a team and the information states with single-integrator dynamics is given by

                                                       (1)

where x_i(t)R is the information state of the i-th agent and u_i(t)R is the control input.

The objective of this work is to propose and analyze consensus protocols to ensure that each agent in the team reaches consensus on a constant or time-varying consensus reference state under directed switching interaction topologies.

Consider that the consensus reference state, denoted by φ(t), satisfies

                                                          (2)

where f(?, ?) is continuously differentiable. The consensus tracking problem with a consensus reference state is solved if x_i(t)→φ(t), i⊥ as t→∞.

The following definition and lemma play an important role in the proof of the main results.

Definition 1 [23]: Let Z denote the set of square matrices whose off-diagonal elements are non-positive, that is,

Then, matrix A is called a non-singular (or singular) M-matrix if AZ and if all its principal minors are positive (or non-negative).

Lemma 1 [23]: If matrix AR^n×n is diagonally dominant (strictly diagonally dominant), i.e.,

then, eigenvalues of A have non-negative (positive) real parts. Additionally, if AZ, matrix A is a singular (non-singular) M-matrix.

3.1 Constant consensus reference state

The case of consensus reference state φ(t) as a constant is considered, i.e., f(t, φ)≡0 in Eq.(2). For information state with single-integrator dynamic in Eq.(1), a consensus tracking protocol with a constant consensus reference state is given as

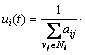
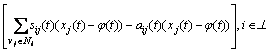  (3)

where φ(t)R is a constant target value. The time sequence of topology varying is T={t₀, t₁, …, t_k, …}. In time interval [t_k-1, t_k), the neighbor set of node v_i is denoted as  In this case, the weighted adjacency element s_ij(t) is a time-varying function:

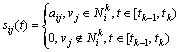                              (4)

Denote the union of G_x(t) on time set T as  and a_ij, i⊥ is the adjacency element of A in the digraph

 Noticing the property of a_ij

that a_ij>0 if and only if v_jN_i, Eq.(3) is equivalent to

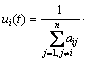
  (5)

Then, system under consensus protocol could be rewritten as

                               (6)

Information-exchange topologies are often dynamic. For example, communication links among agents might be unreliable due to multipath effects and other disturbances. Therefore, conditions under which consensus tracking is achieved over random switching of the communication topologies are investigated.

Theorem 1: Suppose  i.e. deg_in(v_i)>0,

i⊥ for directed graph  then consensus tracking problem with a constant consensus reference state is solved with protocol Eq.(5), i.e.,

                                      (7)

Proof: Let  Then, Eq.(7) is equivalent to  Notice that φ(t) is a constant. Therefore,

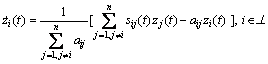       (8)

Define a vector Lyapunov function as

             (9)

where sign(z_i(t)) is a signum function. The time derivative of V(z(t)) along any trajectory of system Eq.(8) is

Thus, the following differential inequality holds:

where

From Lemma 1, it is easy to see that -S is a singular M-matrix with rank of (n-1), so S is a stable matrix. By using the vector comparison theorem, the system Eq.(8) is stable. The proof is completed.

3.2 Time-varying consensus reference state

Assume that the consensus reference state might be a time-varying exogenous signal or evolve according to certain nonlinear dynamics.

Consider the linear multi-agent systems under the following protocol:

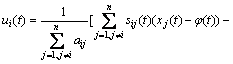
            (10)

where φ(t)R is a smooth and bonded target trajectory. The network dynamic is summarized as

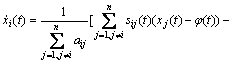
                     (11)

Theorem 2: Suppose  i.e. deig_in(v)>,

0,  for directed graph  then the consensus tracking problem with a time-varying consensus reference state is solved with protocol Eq.(10).

Proof: Define  Then, Eq.(7) is equivalent to  Notice that

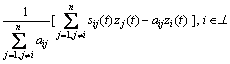  (12)

Therefore, an argument similar to that in the proof of Theorem 1 shows that x_i(t)→φ(t) as t→∞.

Using Theorem 2, multi-agent systems Eq.(11) can track any given time-varying reference state.

Remark 1: In contrast to the strategy in Ref.[20], where the switching topologies including a constant or time-varying consensus reference state are restricted to have a spanning tree, protocols in this work take into account of the general case where switching may be random and unknown in application. It is worthwhile to mention that consensus reference states are available to all agents to overcome the random switching.

3.3 Formation control

The formation control problems which are widely applied in unmanned air vehicles and multiple robots systems are discussed. In fact, the team of agents is required to establish certain formation, where they should keep separation with each other in application. Here, apply one of the consensus tracking protocols to a formation control problem under switching topologies.

In a distributed formation control architecture, trajectory tracking strategies can be employed for each agent. As a result, if each agent can track its desired position accurately, then the desired formation shape can be preserved accurately.

In this type of formation control problem, the target trajectory of the agent i is defined by  where  is constant and  i, j  denotes the desired constant separation between agent i and j. Define the set

as a structure set of formation control.

Consider the linear multi-agent systems under the consensus protocol with a time-varying consensus reference state:

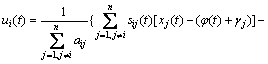
          (13)

The network dynamic is summarized as

             (14)

The following theorem shows that the consensus problem of the formation control of multi-agents is achieved.

Theorem 3: Suppose  i.e. deig_in(v_i)>,

0,  for directed graph  then the formation control problem is solved with protocol Eq.(13), i.e.,

                                (15)

Proof: Define  Note that γ_i is a constant,  Therefore, an argument similar to that in the proof of Theorem 2 shows that  as  The proof of Theorem 3 is completed.

Using Theorem 3, we can design a consensus protocol such that multi-agent system tracks any given trajectory with stable formation. It should be noted that the structure set plays a key role in formation control of multi-agent systems by selecting appropriate structure parameter γ_i.

4 Examples and simulation results

Some simulations of a network with weight of 0-1 are provided to illustrate the effectiveness of this approach.

Example 1: Consider a network with n=6 nodes. In this case, some of the existing communication links fail and some of them are created due to the moving of the agents, as shown in Fig.1. In Fig.2(a), a finite automaton is shown with the set of states {G_a, G_b, G_c, G_d} representing the discrete-states of a network with switching topology as a hybrid system. The hybrid system starts at the discrete-state G_a and switches every t=0.2 s to the next state according to the state machine. Figure 2(b) represents  Choose a_ij= 1 if  and a_ij=0 otherwise, the in-degree of  can be represented as [3, 5, 2, 3, 2, 2].

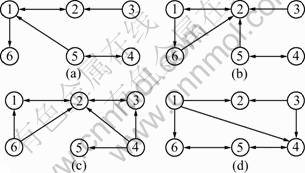
Fig.1 Switching interaction topologies among six agents: (a) G_a; (b) G_b; (c) G_c; (d) G_d

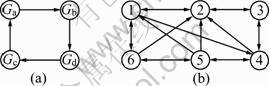
Fig.2 Finite automaton with four states representing discrete- states of network with switching topology (a);    (b)

Supposing that G(t) switches among the set shown in Fig.1, it can be obtained that

The consensus reference state is selected as φ(t)=1 and x(0)=[3, 4, 6, -1, -5, -4] ^T.

Figure 3 shows that the network associated with state switching machine reaches a consensus asymptotically for switching signal t=0.2 s. It is clear that all x_i(t) converge to φ(t) under the consensus protocol.

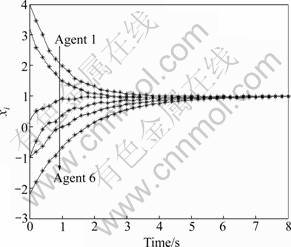
Fig.3 Consensus tracking with constant reference state of six agents

Example 2: Suppose that there is a network with six agents, whose switching topologies are described in

Example 1. Let  with φ(0)=1,

According to Theorem 2, the agents will move asymptotically along the trajectory described by φ(t). And Fig.4 illustrates that the tracking behaviors are quite smooth.

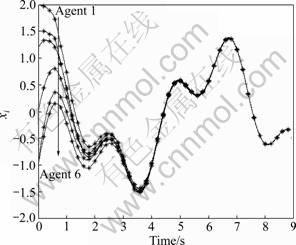
Fig.4 Consensus tracking with time-varying consensus reference state of six agents

Example 3: In the following simulation, chose a network also described in Example 1, maintaining a specific formation during the tracking movement. Set  with φ(0)=3 and x(0)=[3, 4, 6, -1, -5, -4] ^T. According to Theorem 3, six agents will move asymptotically along the target trajectory in the desired formation with switching signal t=0.4 s.

Figure 5 shows that the six agents from arbitrary initial points aim at establishing a specific formation. It is noted that the formation is performed and maintained perfectly during tracking movement.

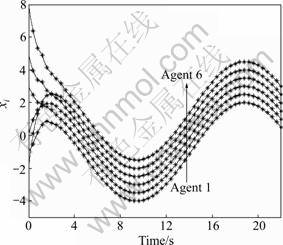
Fig.5 Consensus tracking with time-varying reference state of six agents in formation

5 Conclusions

1) New consensus tracking protocols with a constant and time-varying reference state of multi-agent systems have been proposed. And the convergence analysis of consensus protocols is derived by Lyapunov stability method.

2) The consensus tracking protocol is extended to solve formation control problem.

3) Compared with the existing works, this approach is very simple and effective to solve group formation control and desired trajectory tracking simultaneously. Moreover, this kind of protocol can be used widely in a network of single-integrator under randomly switching topology, which has no requirement of spanning tree in all the dwell time.

References

[1] EREN T, BELHUMEUR P N, MORSE A S. Closing ranks in vehicle formations based on rigidity [C]// Proceedings of the 41st IEEE Conference on Decision and Control. New Haven, CT, USA, 2002: 2959-2964.

[2] VIDAL R, SHAKENIA O, SASTRY S. Formation control of nonholonomic mobile robots with omnidirectional visual servoing and motion segmentation [C]// Proceedings of IEEE Conference on Robotics and Automation. Berkeley, CA, USA, 2003: 584-589.

[3] FAX A, MURRAY R M. Information flow and cooperative control of vehicle formations [J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476.

[4] FOX D, BURGARD W, KRUPPA H, THRUN S. A probabilistic approach to collaborative multi-robot localization [J]. Automatic on Robots, 2000, 8(3): 325-344.

[5] TANNER H G, LOIZOU S G, KYRIAKOPOULOS K J. Nonholonomic navigation and control of multiple mobile manipulators [J]. IEEE Transactions on Robot Automation, 2003, 19(1): 53-64.

[6] YU Wen-wu, CHEN Guang-rong, WANG Zi-dong, YANG Wen. Distributed consensus filtering in sensor networks [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2009, 39(6): 1568-1577.

[7] LOW S H, PAGANINI F, DOYLE J C. Internet congestion control [J]. IEEE Control System Magazine, 2002, 22(1): 28-43.

[8] OLFATI SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays [J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.

[9] REN Wei, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies [J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.

[10] JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules [J]. IEEE Transactions on Automatic Control, 2003, 48(9): 988-1001.

[11] OLFATI SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-agent systems [C]// Proceedings of the IEEE. Hanover, NH, 2007: 215-233.

[12] ZHANG Ya, TIAN Yu-ping. Consentability and protocol design of multi-agent systems with stochastic switching topology [J]. Automatica, 2009, 45(5): 1195-1201.

[13] XIAO Feng, WANG Long. Asynchronous consensus in continuous-time multi-agent systems with switching topology and time-varying delays [J]. IEEE Transactions on Automatic Control, 2008, 53(8): 1804-1816.

[14] LIU Bo, CHEN Tian-ping. Consensus in networks of multiagents with cooperation and competition via stochastically switching topologies [J]. IEEE Transactions on Neural Networks, 2008, 19(11): 1967-1973.

[15] XIAO Feng, WANG Long. Consensus protocols for discrete-time multi-agent systems with time-varying delays [J]. Automatica, 2008, 44(1): 2577-2582.

[16] XIAO Feng, WANG Long and JIA Ying-min. Fast information sharing in networks of autonomous agents [C]// Proceedings of the 2008 American Control Conference, Beijing, 2008: 4388-4393.

[17] SUN Yuan-gong, WANG Long, XIE Guang-ming. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays [J]. Systems and Control Letters, 2008, 57(2): 175-183.

[18] LIN Peng, JIA Ying-min. Average consensus in networks of multi-agents with both switching topology and coupling time-delay [J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(1): 303-313.

[19] REN Wei, BEARD R W, ATKINS E M. Information consensus in multivehicle cooperative control [J]. IEEE Control Systems Magazine, 2007, 27(2): 71-82.

[20] REN Wei. Consensus tracking under directed interaction topologies: Algorithms and experiments [J]. IEEE Transactions on Control Systems Technology, 2010, 18(1): 230-237.

[21] REN Wei, BEARD R W. Distributed consensus in multi-vehicle cooperative control: theory and applications [M]. London: Springer-Verlag, 2008: 55-73.

[22] LI Zhong-kui, DUAN Zhi-sheng, CHEN Guang-rong and HUANG Lin. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint [J]. IEEE Transactions on Circuits and Systems, 2010, 57(1): 213-224.

[23] QU Zhi-hua. Cooperative control of dynamic systems: applications to autonomous vehicles [M]. London: Springer-Verlag, 2009, 167- 172.

(Edited by YANG Bing)

Foundation item: Projects(61075065, 60774045) supported by the National Natural Science Foundation of China; Project supported by the Graduate Degree Thesis Innovation Foundation of Central South University, China

Received date: 2010-07-13; Accepted date: 2010-10-15

Corresponding author: NIAN Xiao-hong, Professor, PhD; Tel: +86-13549668182; E-mail: xhnian@mail.csu.edu.cn