T应力对岩石断裂韧度及扩展路径的影响
周绍青,郭少华,李显方
(中南大学 土木建筑学院,湖南 长沙,410083)
摘 要:为了准确预测岩石类材料复合断裂韧度及裂纹扩展路径,提出结合T应力的修正最大周向应力断裂判据。该修正最大周向应力断裂判据是采用双参数模型(应力强度因子K和T应力)来描述岩石断裂的行为,对岩石类材料复合断裂进行理论计算和实验。结果表明:软岩半圆盘实验所得断裂韧度与传统最大周向应力断裂判据预测结果有较大误差,而修正最大周向应力断裂判据预测结果和实验结果相吻合;当T应力为正并且超过某一定值时,裂纹的扩展路径将发生偏折;T应力对脆性材料断裂试件的断裂韧度和裂纹扩展路径有影响。
关键词:岩石断裂;修正断裂判据;T应力
中图分类号:TU452 文献标识码:A 文章编号:1672-7207(2009)03-0797-06
T-stress’s impact on rock’s fracture toughness and propagation path
ZHOU Shao-qing, GUO Shao-hua, LI Xian-fang
(School of Civil and Architectural Engineering, Central South University, Changsha 410083, China)
Abstract: In order to predict the fracture toughness and propagation of the mixed mode fracture of rocks, the modified MTS (Maximum tangential stress) criterion combined with T-stress was presented. The modified MTS criterion uses a two-parameter model (stress intensity factor K and T-stress) to describe the rock’s fracture. The results show that the soft rock with semi-circular specimens is inconsistent with that of the traditional MTS criterion. The modified criterion can provide accurate predictions for the experimental results. The crack will turn when the T-stress becomes positive and at a considerably high value. The T-stress can influence the cracked specimens’s fracture toughness and the direction of crack’s propagation.
Key words: rock fracture; the modified fracture criterion; T-stress
在断裂力学中,按裂纹的扩展方式分为张开型、滑移型和撕裂型3种,其强度因子分别用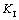 ,
,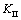 和
和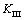 来表示。应力强度因子是一个描述脆性材料裂纹的重要断裂参数。然而,实验结果证明[1-2],除了应力强度因子外,平行于裂纹表面的非奇异应力项即T应力能影响裂纹的发展方向和材料的断裂韧性。Larrsson等[3]认为,在载荷作用下,非奇异应力项的正负和大小与裂尖塑性区的大小和形状密切相关。Rice[4]用有限元法研究了小范围屈服条件下的紧凑拉伸、弯曲、双边裂纹和中心裂纹4种试件的裂尖应力场,发现4种试件的裂面位移、正应力和塑性区尺寸的有限元结果与测试结果之间的相对误差达10%~20%,而引入第2个裂尖参数即T应力,该误差可以消除。Ayatollahi等[5]计算了岩石类材料主裂纹前端的T应力并且提出了裂纹发展方向的判据。但是,对岩石类材料来说,无论是压缩断裂,还是传统Ⅰ,Ⅱ和Ⅲ型断裂,裂纹尖端区域的应力集中是一个普遍存在的客观现象。由于应力集中所引发的裂纹尖端区域的材料局部损伤在微观实验中可以观察到,它通常以微细裂纹的形态存在,这样,在主裂纹前存在微小的分支裂纹[6-9]。目前,人们对裂纹扩展的稳定性研究要么只涉及应力强度因子,要么只涉及主裂纹尖端处的T应力进行分析,而没有考虑裂纹扩展正前方裂尖处的T应力,为了更准确地分析裂纹扩展的路径方向,有必要考虑主裂纹前端的分支微裂纹处的应力强度因子和T应力对裂纹扩展的影响。在此,本文作者采用格林函数求解微裂纹前端应力强度因子和T应力,并对最大周向应力断裂判据(传统MTS判据)进行修正,提出采用双参数(应力强度因子K和T应力)的断裂判据(修正MTS判据)。
来表示。应力强度因子是一个描述脆性材料裂纹的重要断裂参数。然而,实验结果证明[1-2],除了应力强度因子外,平行于裂纹表面的非奇异应力项即T应力能影响裂纹的发展方向和材料的断裂韧性。Larrsson等[3]认为,在载荷作用下,非奇异应力项的正负和大小与裂尖塑性区的大小和形状密切相关。Rice[4]用有限元法研究了小范围屈服条件下的紧凑拉伸、弯曲、双边裂纹和中心裂纹4种试件的裂尖应力场,发现4种试件的裂面位移、正应力和塑性区尺寸的有限元结果与测试结果之间的相对误差达10%~20%,而引入第2个裂尖参数即T应力,该误差可以消除。Ayatollahi等[5]计算了岩石类材料主裂纹前端的T应力并且提出了裂纹发展方向的判据。但是,对岩石类材料来说,无论是压缩断裂,还是传统Ⅰ,Ⅱ和Ⅲ型断裂,裂纹尖端区域的应力集中是一个普遍存在的客观现象。由于应力集中所引发的裂纹尖端区域的材料局部损伤在微观实验中可以观察到,它通常以微细裂纹的形态存在,这样,在主裂纹前存在微小的分支裂纹[6-9]。目前,人们对裂纹扩展的稳定性研究要么只涉及应力强度因子,要么只涉及主裂纹尖端处的T应力进行分析,而没有考虑裂纹扩展正前方裂尖处的T应力,为了更准确地分析裂纹扩展的路径方向,有必要考虑主裂纹前端的分支微裂纹处的应力强度因子和T应力对裂纹扩展的影响。在此,本文作者采用格林函数求解微裂纹前端应力强度因子和T应力,并对最大周向应力断裂判据(传统MTS判据)进行修正,提出采用双参数(应力强度因子K和T应力)的断裂判据(修正MTS判据)。
1 分支微裂纹应力强度因子和T应力
对于图1所示的平面裂纹中的无限小支裂纹,Cotterell等[7]给出了其尖端Ⅰ和Ⅱ型应力强度因子的近似计算公式:

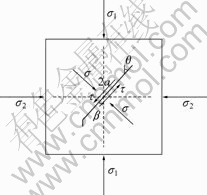
图1 双向压应力中心斜裂纹
Fig.1 Central oblique crack subjected to biaxial compressive loading
主裂纹尖端的应力场方程为[10]:

图2所示为微裂纹尖端的T应力计算简图。其中,微裂纹尖端的T应力采用格林函数求解。
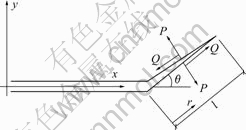
图2 微裂纹受力分析示意图
Fig.2 Geometrical data of a branched crack
Fett等[11]得出的裂纹前端T应力计算公式为:
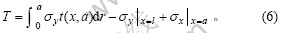
方程(6)只适用于简单的裂纹模式,而不适用于复杂的裂纹如斜裂纹。因此,为描述图2所示的复杂裂纹模式,将方程(6)修正为:

2 T应力对微裂纹断裂路径的影响
2.1 T应力对开裂角的影响
最大周向应力判据最先由Erdogan等[12]提出。该理论指出,裂纹沿着最大周向应力的方向发展和裂纹扩展是由于最大周向应力达到了某一临界值而产生。传统最大周向应力判据仅考虑式(3)中的奇异项。为了更准确地分析裂纹扩展的路径方向,本文作者提出修正最大周向应力判据,该判据除考虑奇异项外,同时考虑T应力的影响。微裂纹尖端应力分布见图3。
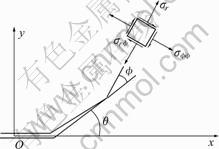
图3 微裂纹尖端应力
Fig.3 Configuration describing near-kink-tip stresses
对于图3所示的裂纹构造和坐标系统,包含T应力的应力展开式可用下式表示:

由此可见,T应力对裂纹的扩展角有较大影响。
对于二维复合断裂模型,在确定参数rc,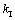 ,
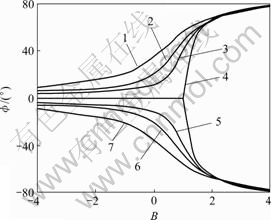
,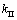 和T时,代入式(10)可求出裂纹扩展角。图4所示为复合断裂模型在
和T时,代入式(10)可求出裂纹扩展角。图4所示为复合断裂模型在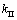 /
/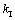 不同时理论预测开裂角与无量
不同时理论预测开裂角与无量
纲B(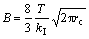 )的关系。
)的关系。
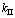 /
/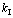 : 1— -0.4; 2— -0.2; 3— -0.1; 4—0; 5—0.1; 6—0.2; 7—0.4
: 1— -0.4; 2— -0.2; 3— -0.1; 4—0; 5—0.1; 6—0.2; 7—0.4
图4 采用最大周向正应力理论预测开裂角
Fig.4 Predicted propagation angle obtained by maximum tangential stress theory
2.2 T应力对断裂韧度的影响
根据最大周向应力断裂判据:
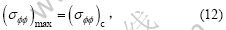
结合式(8)和(12),得到:

式(14)是加入T应力项的最大周向应力断裂判据。若在式(14)中不考虑T应力的影响,则得到传统的最大周向应力断裂判据。
为研究T应力对微裂纹扩展的影响,取主裂纹倾斜角β=30?,围压比为5?1。
修正的最大周向应力断裂判据考虑了复合断裂模型中T应力对断裂韧度的影响。引入无量纲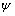 参数,
参数,
 ,其值为0~1。根据方程(14),微裂纹从纯Ⅱ型(
,其值为0~1。根据方程(14),微裂纹从纯Ⅱ型(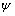 =0)到纯Ⅰ型(
=0)到纯Ⅰ型(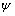 =1)的
=1)的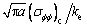 曲线如图5所示。图5中A是关于T应力的无量纲参数,
曲线如图5所示。图5中A是关于T应力的无量纲参数,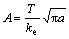 。
。
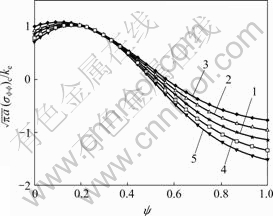
A: 1—0; 2—0.2; 3—0.4; 4— -0.2; 5— -0.4
图5 A不同时周向应力和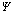 关系图
关系图
Fig.5 Relationship between normalized tangential stress and θ for different A
从图5可以看到,在复合断裂下,T应力的正负和大小对断裂韧度ke有影响。负T应力可以增加复合断裂模型的断裂韧度,而正T应力可以减少其断裂韧度。因此,在复合断裂模型情况下,若改变主裂纹前端的微裂纹角度(即改变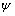 ),就可以相应地改变T应力对断裂韧度ke的影响。在实际工程中,通过改变几何特征和加载情况,增加T应力对复合断裂韧度的影响,便可降低能耗,使T应力有助于裂纹扩展,从而使岩石迅速断裂。
),就可以相应地改变T应力对断裂韧度ke的影响。在实际工程中,通过改变几何特征和加载情况,增加T应力对复合断裂韧度的影响,便可降低能耗,使T应力有助于裂纹扩展,从而使岩石迅速断裂。
3 断裂实验中T应力的影响
Lim等[13]用软岩半圆盘试件测试了在复合断裂模型下的断裂韧度。在该实验中,其断裂韧度普遍低于用传统最大周向应力断裂判据预测的结果。用修正最大周向应力断裂判据预测软岩断裂韧度时,取临界距离rc=3.6 mm能较好地与软岩的断裂韧度相符合。Schmidt[14]给出了临界距离rc计算公式:
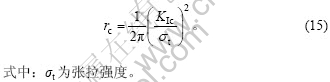
Lim的实验软岩中,参数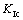 = 2.2 MPa?mm1/2,σt=0.435 MPa。将其代入方程(15),得到该软岩rc为4.07 mm,这与理论值(3.60 mm)非常 接近。软岩半圆盘试件复合Ⅰ/Ⅱ型断裂韧度如图6 所示。
= 2.2 MPa?mm1/2,σt=0.435 MPa。将其代入方程(15),得到该软岩rc为4.07 mm,这与理论值(3.60 mm)非常 接近。软岩半圆盘试件复合Ⅰ/Ⅱ型断裂韧度如图6 所示。
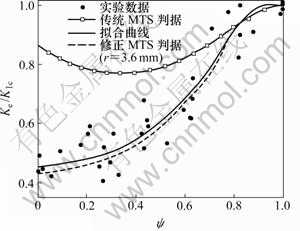
图6 软岩半圆盘试件复合Ⅰ/Ⅱ型断裂韧度
Fig.6 Mixed mode Ⅰ/Ⅱ fracture toughness of semi-circelar specimen made of soft rock
从图6可以看到,当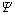 <0.6时,传统最大周向应力断裂判据预测结果和实验结果有较大差距,而采用本文的修正最大周向应力断裂判据所得结果与实验结果相符合。
<0.6时,传统最大周向应力断裂判据预测结果和实验结果有较大差距,而采用本文的修正最大周向应力断裂判据所得结果与实验结果相符合。
采用修正最大周向应力断裂判据也能较好地预测其他材料脆性破坏时的断裂韧度。例如,Ayatollahi等[15]用PMMA半圆盘试件做复合断裂实验。该半圆盘试件半径为50 mm,厚度为5 mm。PMMA的临界距离rc=0.065 mm。图7所示为Ayatollahi[15]的实验结果。可见,传统最大周向应力断裂判据预测结果普遍高于实验值。
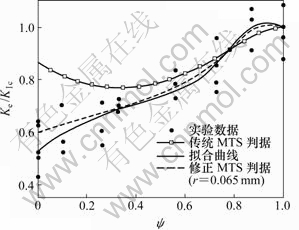
图7 PMMA半圆盘试件复合Ⅰ/Ⅱ型断裂韧度
Fig.7 Mixed mode Ⅰ/Ⅱ fracture toughness of semi-circelar specimen made of PMMA
由于传统最大周向应力断裂判据预测结果误差较大,Lim等[13]在实验中用经验判据和数学方程拟合实验结果。该经验断裂判据如下:

Lim等[13]根据大量实验结果,认为λ=μ=2.25时最符合实验结果。但是,根据经验判据得到的复合断裂韧度在很大程度上依赖于试件的几何特征和加载情况,因此,用修正最大周向应力断裂判据可以不依赖于试件的几何特征和加载情况,而从理论上预测复合断裂韧度。
T应力的正负和数值由试件的几何特征和加载情况确定。当裂纹试件承受复合Ⅰ/Ⅱ模型荷载时,虽然应力强度因子能描述裂纹尖端的应力奇异性,但是,T应力的正负和大小也能够影响其断裂过程。例如,Cotterell等[16-18]指出,在纯Ⅰ断裂模型下,脆性断裂的裂纹扩展路径与T应力的正负有关,T应力为负时裂纹的扩展是稳定的,但当T应力为正时,裂纹的扩展将发生偏转。
Selvarathinam等[19]对裂纹的扩展进行了实验研究,在对PMMA板复合断裂实验中发现,当T应力为正并且超过某一定值时,裂纹的扩展路径将发生偏折,如图8所示。可见,在区域Ⅰ内,裂纹扩展不发生偏折;区域Ⅱ为过渡区;在区域Ⅲ中,裂纹则发生偏折,这说明T应力影响了裂纹的扩展路径。
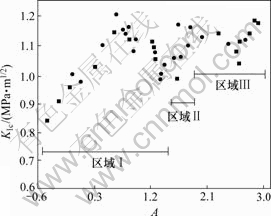
图8 PMMA板中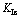 随函数A的变化
随函数A的变化
Fig.8 Relationship between 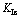 and A for PMMA
and A for PMMA
4 结 论
a. 传统的最大周向应力判据仅考虑奇异项,即裂纹尖端应力场中的Williams特征展开式中仅保留了第1项。为了更准确地分析裂纹扩展的路径方向,提出修正最大周向应力判据除考虑展开式中奇异项外,同时考虑常数项(即T应力)的影响。
b. 实验结果中的断裂韧度低于传统最大周向应力断裂判据预测结果。特别是当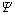 <0.6时,传统最大周向应力断裂判据预测结果与实验结果存在较大的误差。并且在PMMA板复合断裂实验中发现,当T应力为正并且超过某一定值时,裂纹的扩展路径将发生偏折,说明T应力影响脆性材料的断裂韧度和裂纹扩展路径。而本文提出的修正最大周向应力断裂判据由于考虑了T应力的影响,因此,用该判据所得预测结果与实验结果相吻合。
<0.6时,传统最大周向应力断裂判据预测结果与实验结果存在较大的误差。并且在PMMA板复合断裂实验中发现,当T应力为正并且超过某一定值时,裂纹的扩展路径将发生偏折,说明T应力影响脆性材料的断裂韧度和裂纹扩展路径。而本文提出的修正最大周向应力断裂判据由于考虑了T应力的影响,因此,用该判据所得预测结果与实验结果相吻合。
参考文献:
[1] Williams J G, Ewing P D. Fracture under complex stress–the angled crack problem[J]. International Journal of Fracture, 1984, 26(4): 346-351.
[2] Ueda Y, Ikeda K, Yao T. Characteristics of brittle fracture under general combined modes including those under bi-axial tensile loads[J]. Engineering Fracture Mechanics, 1983, 18(6): 1131-1158.
[3] Larrsson S G, Carlsson A J. Influence of non-singular term and specimen geometry on small-scale yielding at crack tips in elastic-plastic materials[J]. Journal of Mechanics and Physics and Solids, 1973, 21(4): 263-277.
[4] Rice J R. Limitations to the small scale yielding approximation for crack tip plasticity[J]. Journal of Mechanics and Physics and Solids, 1974, 22(1): 17-26.
[5] Ayatollahi M R, Aliha M R M. Fracture toughness study a brittle rock subjected to mixed mode Ⅰ/Ⅱ loading[J]. Rock Mechanics and Mining Sciences, 2007, 44: 617-624.
[6] 郭少华, 孙宗颀, 谢晓晴. 压缩条件下岩石断裂模式与断裂判据的研究[J]. 岩石力学与工程学报, 2002, 24(3): 304-308.
GUO Shao-hua, SUN Zong-qi, XIE Xiao-qing. Research on mode and criterion of rock fracture under compressive loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 24(3): 304-308.
[7] Cotterell B, Rice J R. Slightly curved or kinked cracks[J]. Int J Fracture, 1980, 16(1): 155-169.
[8] 赵延林, 曹 平, 文有道. 渗透压作用下压剪岩石裂纹损伤断裂机制[J]. 中南大学学报: 自然科学版, 2008, 39(4): 838-844.
ZHAO Yan-lin, CAO Ping, WEN You-dao. Damage fracture failure mechanism of compressive-shear rock cracks under seepage pressure[J]. Journal of Central South University: Science and Technology, 2008, 39(4): 838-844.
[9] 郭少华, 孙宗颀. 压应力下脆性椭圆型裂纹的断裂规律[J]. 中南工业大学学报: 自然科学版, 2001, 32(5): 383-388.
GUO Shao-hua, SUN Zhong-qi. Fracture law of an elliptical brittle crack under compressive loading[J]. Journal of Central South University of Technology: Natural Science, 2001, 32(5): 383-388.
[10] 匡震邦, 马法尚. 裂纹端部场[M]. 西安: 西安交通大学出版社, 2001.
KUANG Zhen-bang, MA Fa-shang. Crack tip field[M]. Xi’an: Xi’an Jiaotong University Press, 2001.
[11] Fett T, Rizzi G. Weight functions for stress intensity factors and T-stress for oblique cracks in a half-space[J]. Int J of Fract, 2005, 132(1): 9-16.
[12] Erdogan F, Sih G C. On the crack extension in plates under plane loading and transverse shear[J]. J Basic Eng ASME, 1963, 85: 519-525.
[13] Lim I L, Johnston I W, Choi S K, et al. Fracture testing of a soft rock with semi-circular specimens under three-point bending[J]. Int J Rock Mech Min Sci Geomech Abstr, 1994, 31(3): 199-212.
[14] Schmidt R A. A microcrack model and its significance to hydraulic fracturing and fracture toughness testing[C]// Proceedings of 21st US Symposium Rock Mechanics. 1980: 581-590.
[15] Ayatollahi M R, Aliha M R M, Hassani M M. Mixed mode brittle fracture in PMMA: an experimental study using SCB specimen[J]. Mater Sci Eng A, 2006, 417(1/2): 348-356.
[16] Cotterell B, Rice J R. Slightly curved or kinked cracks[J]. Int J Fract, 1980, 16(2): 159-169.
[17] JIE Tong. T-stress and its implications for crack growth[J]. Engineering Fracture Mechanics, 2002, 69(12): 1325-1337.
[18] Ayatollahi M R, Aliha M R M. Wide range data for crack tip parameters in two disc-type specimens under mixed mode loading[J]. Computational Materials Science, 2007, 38(4): 660-670.
[19] Selvarathinam A S, Goree J G. T-stress based fracture model for cracks in isotropic materials[J]. Engineering Fracture Mechanics, 1998, 60(5/6): 543-561.
收稿日期:2008-06-15;修回日期:2008-08-29
基金项目:国家自然科学基金资助项目(10672189)
通信作者:周绍青(1975-),男,湖南永州人,博士,从事岩石力学研究;电话:0731-8877400;E-mail: zsq425100@163.com