基于变形元件的节理岩体压缩损伤本构模型
刘红岩1, 2,黄妤诗1,吕淑然3,张吉宏4, 5
(1. 中国地质大学(北京) 工程技术学院,北京,100083;
2. 西藏大学 工学院,西藏 拉萨,850000;
3. 首都经济贸易大学 安全与环境工程学院,北京,100026;
4. 长安大学 地质工程与测绘学院,陕西 西安,710064;
5. 中国有色金属工业西安勘察设计研究院,陕西 西安,710054)
摘要:为研究节理岩体在压缩荷载作用下的力学响应,基于岩体结构力学观点,把节理岩体在压缩荷载作用下的变形视为岩块变形与节理面变形的叠加,分别采用基于统计损伤模型的弹性损伤变形元件和考虑节理面闭合及滑动的变形元件计算岩块和节理面在压缩荷载作用下的变形,进而建立相应的节理岩体压缩损伤本构模型。并利用该模型讨论节理面弹性模量、最大闭合应变及剪切刚度等对计算结果的影响规律。最后利用该模型对含单条贯通节理的岩体在压缩荷载作用下的应力-应变曲线进行分析计算。研究结果表明:对于可能沿节理面发生剪切滑移的岩体而言,节理面剪切刚度对计算结果的影响最为显著。对本算例而言节理岩体的峰值强度仅为完整岩体的51.5%,反映节理对岩体强度的弱化效应。同时利用该模型得出岩体强度随节理倾角呈现出抛物线变化规律,即当节理倾角在50°~60°之间时,岩体强度最低,该结论与目前的理论及试验研究结果相吻合,从而说明该模型的合理性。
关键词:节理岩体;岩体结构;宏观缺陷;微观缺陷;变形元件;压缩损伤本构模型
中图分类号:TU452 文献标志码:A 文章编号:1672-7207(2014)06-2014-07
A compression damage constitutive model of jointed rock mass based on deformation components
LIU Hongyan1, 2, HUANG Yushi1, L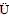 Shuran3, ZHANG Jihong4, 5
Shuran3, ZHANG Jihong4, 5
(1. College of Engineering & Technology, China University of Geosciences (Beijing), Beijing 100083, China;
2. School of Engineering, Tibet University, Lasha 850000, China;
3. School of Safety and Environment Engineering, Capital University of Economics and Business, Beijing 100026, China;
4. School of Geology Engineering and Geomatics, Chang’an University, Xi’an 710064, China;
5. Xi’an Engineering Investigation and Design Research Institute of
China National Non-ferrous Metals Industry, Xi’an 710054, China)
Abstract: In order to study the mechanical response of the jointed rock mass under compression load, the deformation of jointed rock mass under compression load was regarded as the summation of rock block deformation and joint face deformation according to the viewpoint of rock structure mechanics. And the deformation laws of rock block and joint face under compression load were described with the elastic damage deformation component based on the statistical damage model and the joint closure and slippage deformation component, respectively. Then, the corresponding compression damage constitutive model of the jointed rock mass was established. The effect laws of such joint parameters as elastic modulus, maximum closure strain and shear stiffness on the calculation results were discussed with this model. Finally, the stress-strain curve of the rock mass with one single continuous joint under compression load was calculated with this model. The results show that the effect of the joint shear stiffness on the calculation results is the largest to the rock mass which can possibly slip along the joint face. The climax strength of jointed rock mass in this calculation example is only 51.5% of intact rock, which perfectly reflects the deterioration effect of the joint on rock mass strength. Meanwhile, the parabola change law of rock mass strength with the joint dip angle is obtained with this model, which shows that the rock mass strength is minimum when the joint dip angle is between 50°-60°. This conclusion fits very well with the current experimental and theoretical results, which indicates the rationality of this model.
Key words: jointed rock mass; rock mass structure; macroscopic defect; microscopic defect; deformation components; compression damage constitutive model
研究[1-2]表明岩体是一种复杂的天然损伤地质体,其内部包含着从微观到宏观的多尺度缺陷,这些缺陷将对岩体在外力作用下的力学响应产生显著影响。Tang等[3-7]也分别从微观、细观及宏观等角度研究了不同尺度缺陷对岩体力学特性的影响规律,得出了许多有意义的结论。但是,由于岩体本身结构的复杂性,导致现有研究成果仍与实际情况存在一定差距,其中一个重要原因就是对岩体内部缺陷的考虑。众所周知,岩体是一种既包含微裂纹、微孔洞等微观缺陷又包含节理、裂隙等宏观缺陷的地质体,而目前关于岩体本构模型的研究大都仅考虑节理等宏观缺陷对其力学特性的影响[8-9],杨圣奇等[10]通过对含断续预制裂隙脆性大理岩的单轴压缩试验,发现节理裂隙岩体的破坏并非都是沿已有节理裂隙面产生,而可能发生在被节理面切割而成的岩石块体内部,而这种破坏形式正是由于微观缺陷的发展、演化造成的。因此,如何更客观地反映宏、微观两类不同尺度缺陷对岩体力学特性的共同影响则是目前亟待解决的一个重要课题。在这方面,唐春安[11-12]进行了大量的研究工作,把存在于岩体内的节理、裂隙看作是弹性模量极低的一种特殊介质,而把被节理切割而成的岩块看作是由众多强度服从随机分布的细观单元所组成的集合体,进而用连续介质力学方法来处理非连续性问题,获得了良好效果。除此之外,目前很少见到有同时考虑宏、微观缺陷对岩体力学特性影响的文献,为此,本文作者在孙广忠等[13]提出的岩体结构控制论的基础上,综合考虑宏、微观缺陷对岩体力学特性的共同影响,提出一种基于变形元件的节理岩体压缩损伤本构模型。
1 基于变形元件的岩体压缩变形机制及本构方程
20世纪60年代,古德振[14]提出了“岩体结构”概念,提供了将复杂岩体抽象为科学的结构类型分类依据。孙广忠等[13]于20世纪80年代进一步提出“岩体结构控制论”的观点,全面、系统地以“岩体结构控制论”为基础研究了岩体变形、破坏及力学性质的基本规律;提出岩体变形系由岩体材料变形和岩体结构变形共同贡献的,从而建立了较完整的岩体力学结构体系。此后,不少学者根据上述观点把岩体看作是由岩体材料和岩体结构元件两类单元经多种不同方式组合而成,以研究岩体本构模型,如反映岩体蠕变变形的西原模型就是通过5个变形元件(2个弹簧元件、2个黏性元件和1个错动元件)的组合来反映岩体的变形规律[15]。
按照岩体结构控制论的观点,岩体变形主要是由以下2部分组成:一是材料变形包括岩体材料体积单元胀缩变形和形状改变,即岩块的弹性变形;二是岩体结构元件位移和形状改变,即节理面的闭合变形。
(1) 结构体(岩块)的弹性变形机制元件。其变形基本规律可用一种岩石力学元件——弹簧来表示,采用胡克定理来描述,即
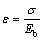 (1)
(1)
式中:ε为应变;σ为应力;Eb为结构体弹性模量。
(2) 结构面(节理面)的闭合变形机制元件。其基本变形规律可用一种岩体结构面闭合变形元件来表示,并遵循衰减法则,即
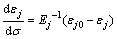 (2)
(2)
式中:d εj为偏结构面应变;d σ为偏应力;Ej为结构面弹性模量;εj0为结构面最大闭合应变;εj为结构面应变。
对式(2)积分可求得[13]
 (3)
(3)
(3) 节理岩体的压缩变形本构方程。在压缩荷载作用下节理岩体的总变形是由岩块的竖直压缩变形和结构面的闭合变形组成,即可把节理岩体看作是由结构体(岩块)的弹性变形元件和结构面的闭合变形元件串联而成。由此可得节理岩体在垂直方向上的压缩变形本构方程为
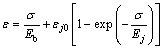 (4)
(4)
虽然式(4)可以反映岩块的弹性变形效应及结构面在压缩荷载作用下的闭合效应,但却存在以下2个明显缺陷:(1) 由于岩体不但包含节理、裂隙等宏观缺陷,而且还包含微裂隙、微孔洞等微观缺陷,而且从微观结构上来看,岩体是由众多强度不等的细观单元所组成,即在较小的应力作用下岩体中也会有少量细观单元会发生破坏,而由式(4)可以看出,由于岩块弹性模量Eb和结构面弹性模量Ej均被视为定值,那么当σ→∞时,岩体总应变也趋于无穷大。该模型是把岩块作为强度无穷大的弹性介质,即认为在任何外力作用下,岩石都不会发生破坏,显然,这种处理方法是不恰当的,外力越大且误差也就越大。(2)式(4)中的节理面闭合变形指的是压缩荷载与节理面垂直时的闭合变形,而实际岩体中的节理面延伸方向并非都与外荷载相垂直。因此,针对上述2个问题必须对式(4)进行修正,以反映岩石微元强度的随机分布特征和节理倾角对岩体压缩变形的影响。
2 综合考虑宏微观缺陷分布特征的岩体单轴压缩变形本构方程
下面分别从岩体微观缺陷分布规律及倾斜节理面受力特征出发,分别研究岩块及节理面的变形计算方法进而对式(4)进行修正,以得出更为合理的节理岩体压缩变形本构方程。
2.1 考虑微观缺陷的岩块变形本构方程
由前述可知,岩块虽然不含有节理、裂隙等宏观缺陷,但是总不可避免地含有微裂隙、微孔洞等微观缺陷。组成岩石的微元强度服从统计分布规律[16],随着外力增加,岩石微元将逐渐发生破坏,进而从宏观上表现出一定的塑性变形特征。若假定微元强度服从Weibull分布,则其变形可表示为[11]
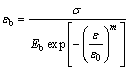 (5)
(5)
式中:Eb为岩块初始弹性模量。在外力作用下岩块弹性模量将随微元的破坏而逐渐减小。
2.2 倾斜节理面压缩变形本构方程
式(4)所反映的节理面垂直于压缩荷载,而在实际工程中并非所有的节理面延伸方向都与外载相垂直,这时节理面在外载作用下不仅产生压缩变形,而且会产生滑移。因此,分析倾斜节理面在压缩荷载作用下的变形更具有普遍性。图1所示为含倾斜节理面的岩体。由图1可见:岩体含1条倾角为α的节理AB,在压缩荷载作用下,节理面上的正应力σα和剪应力τα分别为:
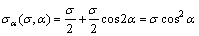 (6)
(6)
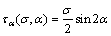 (7)
(7)
那么节理面在外力σ下产生的轴向应变为:
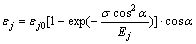 (8)
(8)
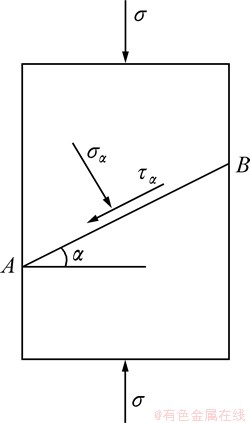
图1 含倾斜节理面的岩体
Fig. 1 Rock mass with one incline joint
综合考虑上述2种情况,可得考虑一般节理岩体在单轴压缩荷载作用下的本构方程为

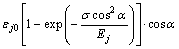 (9)
(9)
式中:Eb和Ej分别为岩块初始弹性模量和节理面弹性模量(也称为节理面闭合模量);m和ε0为拟合系数;εj0为节理面最大闭合应变;α为节理面倾角;σ和ε分别为轴向应力和应变。
由上述分析可以看出,式(9)所表示的轴向应变中不包含节理岩体可能发生的沿节理面剪切滑移而导致的轴向应变,也就是说该式仅适用于半无限大的节理岩体,即在外力作用下仅有轴向应变而没有横向应变。显然,这与大多数实际节理岩体试件的受力情况并不一致,下面将根据实际节理岩体的受力及破坏特征对式(9)进行修正。由节理试件的压缩试验可知,当节理倾角在某一范围内时,试件将沿节理面发生剪切滑移破坏,那么,节理面在剪切滑移过程中将产生剪切位移,进而对试件轴向总应变产生影响,因此,在试件轴向应力应变关系中应考虑其沿节理面产生的剪切位移。根据节理在剪切荷载作用下的本构关系,有[17]
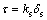 (10)
(10)
式中:ks为节理面切向刚度,Pa/m。
据此,可对式(9)进行修正:

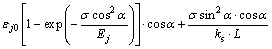 (11)
(11)
其中:L为试件在平面内的高度。
式(11)表明:作用在节理面上的剪应力将使节理面上部试件沿着节理面发生剪切滑移,进而导致整个试件的轴向变形增加。可以看出,在轴向应变计算过程中,不但需要岩块的弹性模量等参数,而且还需要节理面的弹性模量、切向刚度等参数,也即是说节理岩体的强度与变形不但与岩块的参数有关,而且还与节理面的参数有关,这与目前的研究结论是一致的。由于式(11)两端都含有应变,因此,需要采用迭代求解。
3 算例分析
为了说明上述本构模型的合理性,以文献[18]的试验资料为例进行说明。岩石弹性模量Eb=6 949 MPa,m=3.335 2,ε0=0.012 8。含有如图2所示的45°节理,由于没有对实际节理参数进行测试,这里参照有关文献[13]取Ej=1978 MPa,εj0=0.023,ks=20 000 MPa/m,L=0.1 m,则由式(11)可得压缩荷载下的轴向应力-应变曲线如图3所示。由图3可以看出:当岩体内含有节理等宏观缺陷时,其力学性质明显软化,表现为在产生同样的轴向应变时,所需应力大大减小。完整岩体的峰值强度约为46.36 MPa,而相应的节理岩体峰值强度则仅为23.88 MPa,约为完整岩体的51.5%。这说明节理存在大大削弱了岩体强度,降低了其刚度,增大了其柔性。
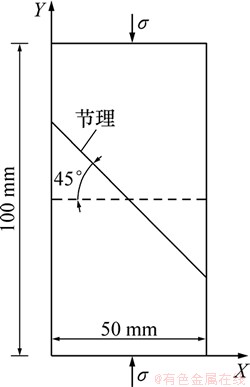
图2 计算模型示意图
Fig. 2 Calculation model
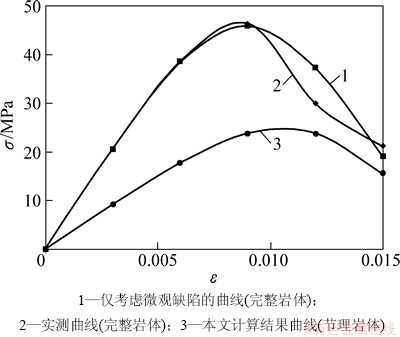
图3 计算应力-应变曲线
Fig. 3 Calculation stress-strain curves
3.1 节理力学参数对计算结果的影响分析
由式(11)可以看出:节理面参数如节理面弹性模量、最大闭合应变及剪切刚度等对计算结果均有一定影响,下面对上述参数对计算结果的影响规律进行探讨。这里仍以图2所示的计算模型为例,假定当某一参数变化,其他2个参数均保持不变,结果如图4~6所示。由图4可以看出:试件应力-应变曲线随节理面最大闭合应变变化不大,而且试件峰值强度与其呈线性关系,这也可由式(11)看出。当节理面最大闭合应变由0.005增加到0.023时,试件最大峰值由24.09 MPa下降到23.88 MPa,下降幅度约为0.87%,因此下降幅度很小,可以认为在本算例中节理面最大闭合应变对计算结果影响很小。但应指出的是,由于本算例中节理倾角为45°,故在压缩荷载作用下试件主要发生沿节理面的滑移破坏,而垂直压缩变形相对很小,因此节理面最大闭合应变对计算结果的影响就相对较小,可以推断当节理走向与荷载垂直时,其对计算结果的影响程度则会相对较大。同样由图5可以看出节理弹性模量对试件应力-应变曲线的影响也呈现出类似的规律。随节理面弹性模量的增加,试件峰值强度逐渐趋于某一定值,这说明当节理面弹性模量增加到一定程度后,其对试件力学特性的影响就不甚明显。由图6可以看出:随节理面剪切刚度增加,试件应力-应变曲线包括峰值强度及峰值应变均有明显变化,即随着节理面剪切刚度增加,试件峰值强度明显增加,对应的实际物理过程为随着节理面剪切刚度增加,在同样的轴向荷载作用下试件沿节理面的滑移变形就越小,进而提高其轴向抗压强度。随着节理面剪切刚度增加,试件峰值强度的变化幅度逐渐减小,这也说明当节理面剪切刚度增加到一定程度后,其对试件力学特性的改善程度不甚明显。
3.2 节理倾角对岩体强度的影响分析
计算模型仍如图2所示,取节理倾角分别为0°,30°,45°,60°及90°。所用计算参数为:b=0.05 m,L=0.1 m,Eb=6 949 MPa,m=3.335 2,ε0=0.012 8,Ej= 6 000 MPa,εj0=0.005,ks=20 GPa/m。需要说明的是这里εj0取值较小。其主要原因是为了和上述计算结果进行对比分析,总应变仍取为0.015,这样岩块变形在整个试件总变形中所占的比例就会增加,进而可以更好地研究岩块及节理面对整个试件的总体变形及强度的影响。由图7可以看出:由式(11)得出的应力-应变曲线及强度变化规律与Jaeger等[19]的试验结果十分类似,即随着节理倾角在0~90°变化,试件单轴峰值抗压强度呈开口向上的抛物线规律变化,当节理倾角约为60°时,其单轴抗压峰值强度最低,而0°和90°时的峰值强度基本相等。这也从另一侧面说明了该模型的正确性。
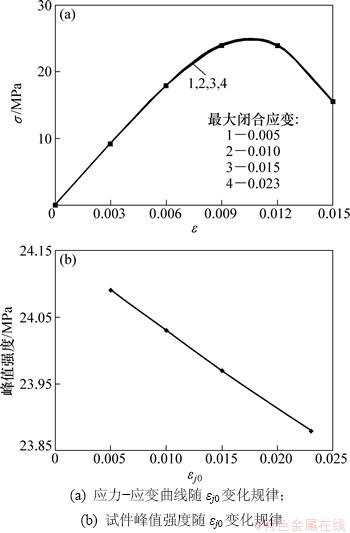
图4 εj0对试件力学特性的影响规律
Fig. 4 Effect of εj0 on sample’s mechanical property
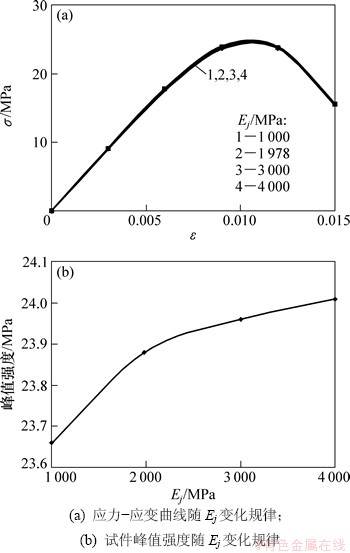
图5 Ej对试件力学特性的影响规律
Fig. 5 Effect of Ej on sample’s mechanical property
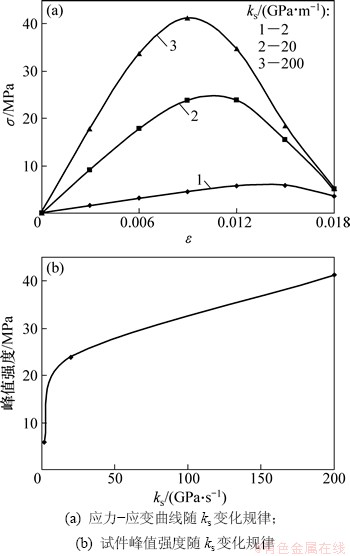
图6 ks对试件力学特性的影响规律
Fig. 6 Effect of ks on sample’s mechanical property
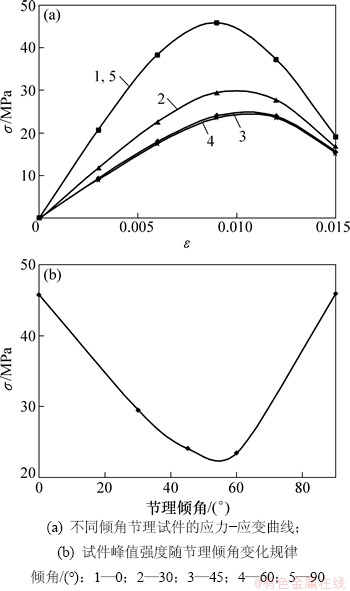
图7 不同倾角节理试件的力学特征
Fig. 7 Samples’ mechanical property with different joint dip angles
4 结论
(1) 所提出的节理岩体压缩损伤本构模型同时考虑了岩体内部存在的宏、微观两类不同缺陷对岩体力学特性的影响。基于岩体结构力学观点,把岩体变形视为岩块变形与节理面变形之和,并分别采用基于统计损伤模型的弹性损伤变形元件和考虑节理面闭合及滑动的变形元件描述岩块和节理面在压缩荷载作用下的变形规律。
(2) 宏观节理的存在大大削弱了岩体强度,对本算例而言,节理岩体的峰值强度仅为相应完整岩体的51.5%。对可能发生沿节理面滑动的岩体而言,节理面剪切刚度对计算结果的影响最大。
(3) 利用该模型对含不同倾角节理的岩体强度进行了分析计算,得出了节理岩体峰值抗压强度随节理倾角呈抛物线的变化规律,这与相关试验结果和已有理论分析结果较一致,说明了该模型的合理性。该模型的提出有望为节理岩体强度及变形计算提供一种新思路。
参考文献:
[1] 易顺民, 朱珍德. 裂隙岩体损伤力学导论[M]. 北京: 科学出版社, 2005: 1-7.
YI Sunmin, ZHU Dezhen. Introduction of cracked rock mass damage mechanics[M]. Beijing: Science Press, 2005: 1-7.
[2] Krajcinovic D. Damage mechanics[J]. Mechanics of Materials, 1989(8): 117-197.
[3] Tang C A. Numerical studies of the influence of microstructure on rock failure in uniaxial compression-PartⅠ: Effect of heterogeneity[J]. Int J Rock Mech Min Sci, 2000, 37: 555-569.
[4] Zhou J W, Xu W Y, Yang X G. A microcrack damage model for brittle rocks under uniaxial compression[J]. Mechanics Research Communications, 2010, 37: 399-405.
[5] Xie N, Zhu Q Z, Xu L H, et al. A micromechanics-based elastoplastic damage model for quasi-brittle rocks[J]. Computers and Geotechnics, 2011, 38: 970-977.
[6] Hamdi E, Romdhane N B, Le Cleach J M. A tensile damage model for rocks: Application to blast induced damage assessment[J]. Computers and Geotechnics, 2011, 38: 133-141.
[7] Paliwal B, Ramesh K T. An interacting micro-crack damage model for failure of brittle materials under compression[J]. Journal of the Mechanics and Physics of Solids, 2008, 56: 896-923.
[8] WANG T T, Huang T H. A constitutive model for the deformation of a rock mass containing sets of ubiquitous joints[J]. Int Journal of Rock Mechanics & Mining Sciences, 2009(46): 521-530.
[9] Swoboda G, Shen X P, Rosas L. Damage model for jointed rock mass and its application to tunneling[J]. Computers and Geotechnics, 1998, 22(3/4): 183-203.
[10] 杨圣奇, 戴永浩, 韩立军, 等. 断续预制裂隙脆性大理岩变形破坏特性单轴压缩试验研究[J]. 岩石力学与工程学报, 2009, 28(12): 2391-2404.
YANG Shengqi, DAI Yonghao, HAN Lijun, et al. Uniaxial compression experimental research on deformation and failure properties of brittle marble specimen with pre-existing fissures[J]. Chinese Journal of Rock mechanics and Engineering, 2009, 28(12): 2391-2404.
[11] 唐春安. 岩石破裂过程中的灾变[M]. 北京: 煤炭工业出版社, 1993: 20-27.
TANG Chunan. Catastrophe in rock unstable failure[M]. Beijing: Coal Industry Press, 1993: 20-27.
[12] TANG Chunan. Numerical simulation of progressive rock failure and associated seismicity[J]. Int J Rock Mech Min Sci, 1997, 34(2): 249-261.
[13] 孙广忠,孙毅. 岩体力学原理[M]. 北京: 科学出版社, 2011: 44-50.
SUN Guangzong, SUN Yi. Principle of rock mass mechanics[M]. Beijing: Science Press, 2011: 44-50.
[14] 谷德振. 岩体工程地质力学基础[M]. 北京: 科学出版社, 1983: 222-240.
GU Dezheng. Fundamentals of rock engineering geomechanics[M]. Beijing: Science Press, 1983: 222-240.
[15] 陶波, 伍法权, 郭改梅, 等. 西原模型对岩石流变特性的适应性及其参数确定[J]. 岩石力学与工程学报, 2005, 24(17): 3165-3171.
TAO Bo, WU Faquan, GUO Gaimei, et al. Flexibility of visco-elastoplastic model to rheological characteristics of rock and solution of rheological parameter[J]. Chinese Journal of Rock mechanics and Engineering, 2005, 24(17): 3165-3171.
[16] Krajcinovic D, Silva M A G. Statistical aspects of the continuous damage theory[J]. Int J Solids Structures, 1982, 18(7): 55-562.
[17] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002: 133-140.
XIA Caichu, SUN Zongqi. Engineering rock mass joint mechanics[M]. Shanghai: Tongji University Press, 2002: 133-140.
[18] 凌建明, 孙钧. 脆性岩石的细观裂纹损伤及其时效特征[J]. 岩石力学与工程学报, 1993, 12(4): 304-312.
LING Jianming, SUN Jun. On mesocrack damage of brittle rocks and its time-dependent characteristics[J]. Chinese Journal of Rock mechanics and Engineering, 1993, 12(4): 304-312.
[19] Jaeger J, Cook N. Fundamentals of rock mechanics[M]. London: Chapman and Hall LTD, 1969: 100-105.
(编辑 陈爱华)
收稿日期:2013-08-06;修回日期:2013-11-10
基金项目:国家自然科学基金资助项目(41002113,41162009);教育部科学技术研究重点项目(211175);中央高校基本科研业务费专项资金资助项目(2010ZY45);2011年度北京市属高等学校人才强教深化计划人才创新团队项目(PHR201107143)
通信作者:刘红岩(1975-),男,河南扶沟人,博士,教授,从事岩石力学研究;电话:13718521906;E-mail:lhyan1204@126.com