J. Cent. South Univ. (2016) 23: 3262-3272

DOI: 10.1007/s11771-016-3392-6

Mode of overlying rock roofing structure in large mining height coal face and analysis of support resistance

WU Feng-feng(吴锋锋), LIU Chang-you(刘长友), YANG Jing-xuan(杨敬轩)

School of Mines, Key Laboratory of Deep Coal Resource of Mining of Ministry of Education

(China University of Mining & Technology), Xuzhou 221116, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: The mining space of large mining height coal face is large, the range of movement and caving of rock strata is large and the stability of supports at coal face is low and damage rate of supports is high, which significantly affects the safe and efficient production of coal mines. By similar simulation experiment and theoretical analysis, the mode of fractured roofing structure of large mining height coal face and the method of determination of reasonable support resistance of the support was evaluated. Analysis shows that the structural mode of “combined cantilever beam – non-hinged roofing – hinged roofing” of the large mining height coal face appears at the roofing of large mining height coal face. The supporting factor of caved gangue at the gob is introduced, the calculating equations of the fractured step distance of roofing were derived and conventional calculating method of caved height of roofing was corrected and the method of determination of the length and height of each structural area of the roofing was provided. With reference to the excavating conditions at Jinhuagong coal mine in Datong minefield, the dimensions of structural areas of the roofing of the coal face were determined and analyzed, and reasonable support resistance of the height coal face was acquired. By selecting Model ZZ13000/28/60 support and with procedures of advanced pre-cracking blasting, the safe production of large mining height coal face was assured.

Key words: large mining height; roof structure; roof model; roof fracturing distance; support resistance

1 Introduction

The coal reserves in China are abundant. The thickness of coal seam in numerous minefields is more than 3.5 m, i.e. Xingtai and Kailuan minefields in Hebei Province, Xuzhou minefield in Jiangsu Province, Longkou and Yanzhou minefields in Shandong Province, Huaibei minefield in Anhui Province, Fuxin minefield in Liaoning Province, Shuangyashan minefield in Heilongjiang Province, Yima minefield in Henan Province, Xishan, Datong, Luan, Jincheng and Yangquan minefields in Shanxi Province as well as Tongchuan minefield in Shaanxi Province [1-3]. Therefore, the excavating techniques of coal seam with large mining height determine the development of technological level and the utilization of economic benefit of the entire coal mining industry in China [4-8]. Due to the advantages of high resource recovery and small amount of gas discharge of the excavation of coal seam with large mining height, it has become the direction of development and primary technical approach of the safe and efficient excavation of minefields in China [9-10]. In recent decades, significant breakthrough had been achieved in the development of associated equipment for the excavation of minefield with large mining height which significantly accelerated the development of excavating techniques for thick coal seam with large mining height [4-5]. However, in-situ measurement and abundant theoretical studies showed that with the increase of mining height of the coal seam and the height of support, the stability of the surrounding rock support system weakened and the accident rate exceeded 19% [11-12]. Common incidents of run over and damage of support occurred due to insufficient working resistance of support at the coal face [12]. For example, Jinhuagong coal mine is one of the large scale minefields owned by Datong Coal Mine Group in China which locates at 12.5 km to the west of Datong City. The area of minefield is 41 km², the designed production capacity is 4.5×10⁶ per year and the average mining height of coal seam is 5.7 m. The lithological character of the roofing is mainly sandy strata with high hardness. During the back stoping period of the coal face, a total of three support crushing incidents occurred and a total 21 d normal production was affected [13].

Due to the complexity of the conditions of occurrence as well as the specialty of the excavating techniques for large mining height coal seam, when guided by conventional mining pressure and strata control theory, it is likely that the activity of coal face roofing is unclear and the mechanism of mining pressure appearance is unknown, thus hindering the efficient and safe production of the coal mine. Therefore, it is of great theoretical significance and practical value to evaluate in depth the pattern of fracturing and destabilization overlying rock strata of coal face with large mining height and the structure of the roof structure, reveal the relationship between support and surround rocks in large mining height coal face and thus provide effective and rational roof control techniques.

2 Similar simulation experiment and roof structural model at large mining height coal face

2.1 Similar simulation experiment and analysis of large mining height coal face

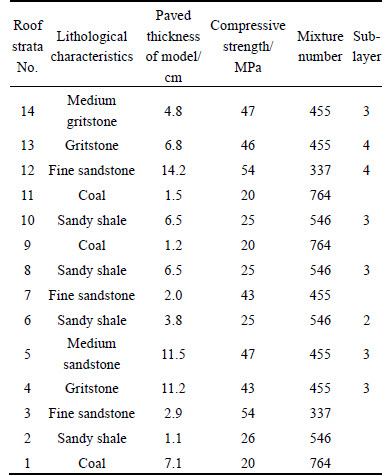
In order to evaluate the characteristics of movement and structural mode of overlying rock roofing in large mining height condition, large mining height coal face 8218 at Jinhuagong coal mine was selected as a background to conduct physical similar simulation experiment. 2D plane stress experimental station was used to conduct similarity analysis. The selection of similarity constants as well as the physical and mechanical parameters and mixture are shown in Tables 1 and 2 [14].

The experiment shows the following results.

1) During the advancement of 20 m of the coal face, the immediate roof fractured in a periodic order and act directly on the support of the minefield in the mode of combined cantilever beam structure. The overlying rock strata above the immediate roof remained intact. With the increase of distance of advancement, different amount of settlement of the sub-layers of the overlying rock strata led to the delamination of the sub-layers.

2) When the coal face advanced to 70 m, the collapsed height at the gob increased. The caving gangue gradually filled the space of the gob to support the fractured blocks of the overlying rock strata. However, as the caving gangue was in the initial extrusion stage, the compactness was low and the amount of extrusion was large; the settlement of roofing exceeded the ultimate allowable settlement between the fractured blocks and thus hinged rock-beam structure could not be formed between the blocks. Instead, non-hinged rock-beam structure existed.

Table 1 Primary similarity constants of similar simulation experiments

Table 2 Physical and mechanical parameters of coal seam with large mining height

3) When the coal face advanced to 120 m, the space of overlying rock strata reduced and the amount of extrusion of the caving gangue at the gob became was limited. The allowable settlement of the fractured roofing was smaller than the ultimate amount of rotation of the overlying rock strata. In addition, large extrusion existed between the fractured blocks. As a result, masonry beam structure was formed between the fractured blocks of the high roofing.

2.2 Proposal of structural model of large mining height roofing

Affected by the gob space of large mining height coal face, the fractured structure of roofing of the gob has the following characteristics:

1) During the initial mining period of the coal face, the immediate roofing existed in the form of combined cantilever beam structure. Affected by the lithological characteristics of the roofing, there is a certain amount of difference in the suspended length of the combined cantilever beam structure. For normal soft roofing, such as mud stone, shale and sandy shale, the fracturing line lies on the tail beam of the support and the support of the coal face mainly carries the weight of the overlying rock. For harder roofing, such as sandstone, limestone and glutenite, the fracturing line normally lies behind the tail beam of the support by a certain distance and cantilever structure is formed. In this case, apart from sustaining the weight of the collapsed roofing, the support is also subjected to the moment of the cantilever roofing.

Fig. 1 Damage mode of overlying rock during advancement of coal face:

2) The blocks of the non-hinged roofing structure are regularly arranged and there is no compressive action between the blocks. For normal soft roofing, such as mud stone, shale and sandy shale, the non-hinged roofing structure transforms to combined cantilever beam structure. For harder roofing, such as sandstone, limestone and glutenite, the fractured dimensions of the non-hinged roofing structure are large and the supporting action from the gangue in the gob increases. As a result, the effect on the underneath combined cantilever beam structure is reduced.

3) When the hard rock strata above the non-hinged roofing fractures, the allowable settlement is limited and the fractured blocks forms hinged roofing structure due to mutual extrusion. Unconnected fracturing appears on the overlying roofing and the roofing is primarily subjected to bending settlement.

The “combined cantilever beam structure – non-hinged roofing structure – hinged roofing structure” model for the overlying roofing of large mining height coal face is shown in Fig. 2.

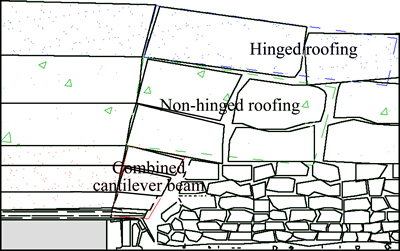
Fig. 2 Model for overlying roofing of large mining height coal face

3 Determination of structural area for large mining height coal face roofing structure

3.1 Determination of collapsed height of roofing in gob

On the basis of the structural mode of the roofing of large mining height coal face, it is an important premise of selecting the type of coal face support to reasonably determine the area of different roofing structure. Thus, different roofing structures of the large mining height coal face are discussed and relevant criterion of determination is provided.

It is known that when the following relation is met, the ith sub-layer of the roofing will stop fracturing upward [15].

                            (1)

where i and j are the numbers of sub-layers of the roofing; κ_j is the residual bulking factor of the jth sub-layer of the fractured roofing; h_j is the thickness of the jth sub-layer of roofing; h_m is the mining height of coal seam.

When the calculated sub-layers of roofing meets Eq. (1), the sub-layers of the overlying roofing will stop fracturing and the collapsed height of the roofing at the gob will be:

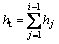                                  (2)

where h_t is the collapsed height of the gob of large mining height coal face.

3.2 Determination of area of combined cantilever beam structure of roofing

1) Determination of length of cantilever beam structure of roofing

When the roofing of large mining height coal face is in the mode of cantilever beam, the step distance of the periodic fracturing of the roofing [15-16] is

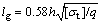                            (3)

where l_g is step distance of the periodic fracturing of the roofing sub-layers; h is the thickness of the sub-layers; [σ_t] is the ultimate tensile strength of the roofing; q is the load on the roofing.

It is evident that the equation matches favorably with the analytical results of conventional mining pressure theory [16]. Therefore, the length of the combined cantilever structure of the roofing can be determined as

L_z=max(l_gi)                                  (4)

where L_z is the length of the combined cantilever beam; l_gi is the step distance of the periodic fracturing of the ith sub-layer of the roofing.

Due to the support of underneath roofing, the sub-layers of the overlying roofing will not fracture and the step distance of fracturing of the overlying roofing sub-layers mainly depends on the maximum suspended dimensions of the underneath sub-layers. Therefore, the combined cantilever beam structure appears to be inverted trapezoidal in overall shape.

2) Determination of thickness of cantilever beam structure of roofing

The condition of gob filled with caved gangue at large mining height coal face is selected as the criterion of determination of the thickness of cantilever beam structure of the roofing:

                                  (5)

where H_z is the thickness of the combined cantilever structure of the roofing; h_i is the thickness of the sub-layers of the combined cantilever structure.

In Eq. (5), h_i needs to meet the condition as

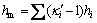
where 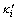is the bulking factor of fractured roofing sub-layers. In the condition that the lithological characteristics of the roofing is similar, the bulking factor of the fractured roofing blocks which caved to the gob is basically identical. Thus, the height of the combined cantilever beam structure is

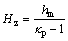                                 (6)

where κ_p is the average bulking factor of the fractured roofing sub-layers.

The relationship between the height of combined cantilever beam of the roofing, the mining height of the coal seam and the bulking factor of the gangue at the gob is demonstrated in Fig. 3.

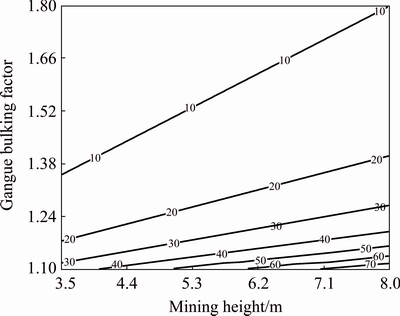
Fig. 3 Relationship between mining height of coal seam and bulking factor of gangue at gob

It is clear from Fig. 3 that under the same bulking factor of the caved gangue at the gob, the height of the combined cantilever beam structure of the roofing increased with the increase of mining height of the coal seam. Furthermore, when the bulking factor of the gangue is small, with the increase of mining height, the height of the combined cantilever beam of the roofing increases at the faster rate. The smaller the bulking factor of the gangue, the larger the gradient of increase of the height of the combined cantilever beam of the roofing with the increase of the mining height of the coal seam.

3.3 Determination of area of non-hinged roofing structure

1) Determination of length of non-hinged roofing structure

Non-hinged roofing structure is a type of transitional structural form between cantilever structure and hinged roofing structure. Due to the supporting effect of the caved gangue at the gob, the effect of gangue support should be considered during the calculation of periodic fractured dimensions of the roofing. Therefore, the fractured dimension of the roofing structure [16] is

, 0≤λ<0.5                    (7)

where l_f is the periodic fracturing dimension of non-hinged roofing structure; λ is the support factor of the gangue at the gob.

Equation (7) shows that when subjected to a certain amount of load on the roofing, the dimensions of the fractured blocks depend on the thickness of occurrence of the roofing as well as the degree of support of the gangue at the gob. The larger the mining height is, the stronger the supporting effect of the gangue at the gob provides and the larger the periodic fractured dimensions of the roofing are. As the degree of support provided by the gangue at the gob is limited by the mining height of the coal seam, the periodic fracturing dimension of the non-hinged roofing structure is also indirectly affected by the mining height of the coal seam.

The effect of mining height of coal seam can be directly reflected on the support factor of caved gangue at the gob. Therefore, the experimental result of uniaxial extrusion of gangue is referred to and it is assumed that there is logarithmic relationship between the support factor of the caved gangue at the gob and the mining height of the coal seam [17-18], i.e.

h_m=m₁lnλ+n₁                                 (8)

where m₁ and n₁ are respectively constant parameters to be determined by experiment. It was determined by experimental analysis that m₁ is -2.21 and n₁ is 0.46 [18-19].

As a result, the relationship between the support factor of the caved gangue at the gob and the mining height of the coal seam is shown in Fig. 4.

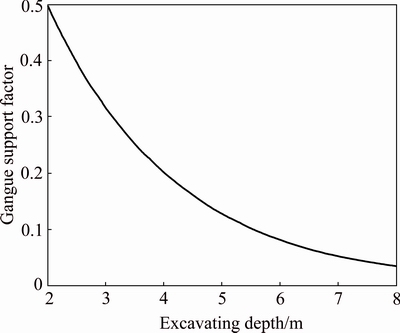
Fig. 4 Relationship between support factor of caved gangue at gob and mining height of coal seam

It is clear from Fig. 4 that the larger the mining height of the coal seam is, the harder the gob space after large mining height excavation to be filled on time is, and thus the smaller the supporting effect of gangue is provided for the non-hinged roofing structure.

Correlating Eq. (7) and Eq. (8), the relationship between the periodic fracturing dimensions of the non-hinged roofing structure and the mining height of the coal seam is demonstrated in Fig. 5.

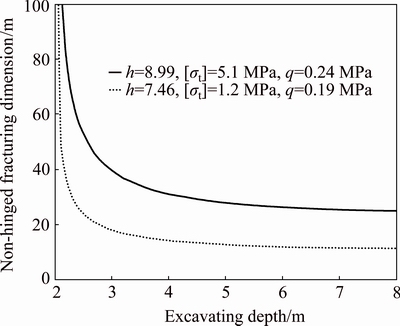
Fig. 5 Relationship between fracturing dimensions of non-hinged roofing structure and mining height of coal seam

It is clear from Fig. 5 that with the increase of mining height of the coal seam, the periodic fracturing dimensions of the non-hinged roofing structure reduced. In particular, for the excavation of coal seam with large mining height, the fractured dimension of the non-hinged roofing structure is basically stable. For the excavation of medium-thick coal seam, with the reduction of mining height of the coal seam, the periodic fracturing dimensions of the roofing increased significantly. The above phenomenon is due to the fact that the gob space under large mining height excavation is large and the caved gangue is able to fill the gob space only when the roofing caves to a certain height. At such moment, affected by large caving height of the roofing, the compactness of the gangue is relatively small and the load-carrying capacity of the caved gangue under the loading effect of overlying rock roofing is low. As a result, the fracturing dimension of the roofing is small. In contrary, when the mining height of the coal seam is small, the gob space can be fully filled when the roofing caved to a smaller height. The caved gangue at the gob soon possesses high supporting effect under the rotation and compaction of the overlying rock roofing and thereby delays the fracturing of the overlying rock roofing. As a result, large periodic fracturing dimension is produced by the non-hinged roofing structure. The length of the non-hinged roofing structure can be therefore determined as

L_f=max(l_fi)                                  (9)

where L_f is the length of the non-hinged roofing structure; l_fi is the step distance of the periodic fracturing of the ith sub-layer of the non-hinged roofing.

2) Determination of thickness of non-hinged roofing structure

Non-hinged roofing structure is defined with comparison to the overlying hinged roofing structure. Therefore, it is determined that the indicator of non-hinged roofing structure is the condition of destabilization of the hinged roofing structure.

The stability of the hinged roofing structure is affected not only by the load of surround rock, condition of occurrence as well as the physical and mechanical characteristics of the rock strata, but also the limitation of gob space. Apparently, if the gob space is small, the rotational deformation of the hinged structure of the overlying rock roofing is limited and the load of overlying rock is large. In this condition, the hinged structure of the roofing is not easy to destabilize. Therefore, the condition of transformation of the hinged structure of the roofing under certain load depends on the gob space. In other words, the determination indicator of the thickness of the non-hinged roofing structure is required to meet the following equation:

△H>w_g                                    (10)

where △H is the compressive deformation of the gangue at the gob; w_g is the ultimate rotational settlement of the hinged structure of the roofing. It is known that the ultimate rotational settlement of the hinged structure of the roofing can be represented by [2-3]

w_g=l_gsinβ                                  (11)

where l_g is the periodic fracturing dimension of the hinged roofing; β is the rotational angle of the fractured blocks.

With reference to the condition of rotational critical destabilization of the roofing, the determination relationship of the ultimate rotational angle of the fractured blocks of the hinged roofing is given as

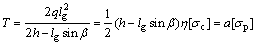    (12)

where T is the compressive force between the blocks of the hinged roofing; η is an experimental constant; a is the length of compressive contact area of the blocks; [σ_c] is the compressive strength of the roofing; [σ_p] is the extrusion strength of the roofing.

The ultimate rotational angle of the hinged roofing can be calculated by Eq. (12) as

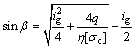                     (13)

where i_g is the block ratio of the fractured blocks of the hinged roofing with a value of h/l_g.

Experimental analysis showed that Hooke’s law applies between the compressive deformation of the caved gangue at the gob and the load [20], thus

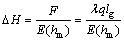                       (14)

where E(h_m) is the compressive modulus of the caved gangue at the gob calculated as a function of mining height h_m of the coal seam.

Correlating Eq. (10) to Eq. (14), the condition of the transformation of the ith sub-layer of the hinged roofing towards non-hinged roofing structure is

                       (15)

where λ_i is the support factor of the gangue at the gob of the ith sub-layer of the roofing; η_i is the experimental extrusion constant of the ith sub-layer of the hinged roofing; [σ_ic] is the compressive strength of the ith sub-layer of the hinged roofing; q_i is the load of the ith sub-layer of the hinged roofing; h_i is the thickness of the ith sub-layer of the hinged roofing; l_gi is the fractured block dimensions of the ith sub-layer of the hinged roofing.

According to the uniaxial compression experimental results of the gangue blocks, it is similarly deemed that logarithmic relationship exists between the compressive modulus of the caved gangue at the gob and the mining height of the coal seam [17-18], thus

E=m₂+lnh_m+n₂                              (16)

where m₂ and n₂ are relevant constants to be experimentally determined. Experimental analysis showed that m₂ is -361.7 and n₂ is 842.8 [18-19].

As a result, the relationship between the compressive modulus of the caved gangue at the gob and the mining height of the coal seam is shown in Fig. 6.

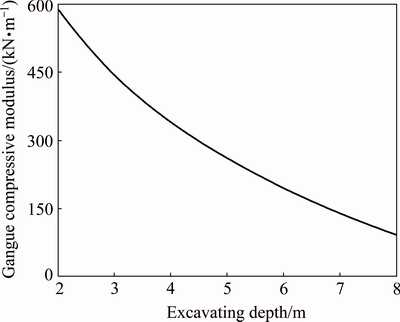
Fig. 6 Relationship between compressive modulus of caved gangue at gob and mining height of coal seam

Correlating Eq. (8), Eq. (15) and Eq. (16) and with reference to the characteristics of the fractured blocks of the roofing sub-layers, it can be determined if the hinged structure of the ith sub-layer of the roofing transforms to non-hinged roofing structure. Accordingly, the overlying sub-layers of the roofing above the combined cantilever beam structure is determined bottom-up until the condition in Eq. (15) does not meet by the (n+1)th sub-layer, when the thickness of the non-hinged roofing structure can be acquired as

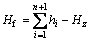                             (17)

where H_f is the thickness of the non-hinged roofing structure.

3.4 Determination of area of hinged roofing structure

1) Determination of length of hinged roofing

Due to extrusion force between the blocks, the normal stress at the complete roofing section is increased and the tensile strength of the blocks of the roofing is improved. From the perspective of equivalent improvement of the compressive strength of the rocks and with consideration of the effect of support of gangue at the gob, the fractured block dimension of the hinged roofing is calculated as [16]

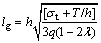, 0≤λ<0.5                  (18)

Correlating Eq. (12) and Eq. (18), the implicit equation about the fractured blocks of the hinged roofing is:

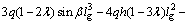
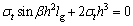                 (19)

The theoretical analytical solution of Eq. (19) is extremely complex. Matlab software was used to analyze the equation and the relationship between the fractured dimensions of the roofing and the support factor of the gangue at the gob under a certain amount of load on the rock strata is calculated and demonstrated in Fig. 7.

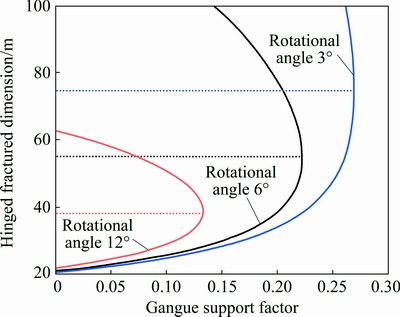
Fig. 7 Relationship between fractured dimensions of roofing and support factor of gangue at gob

The meaningless negative and complex roots of the equations are excluded from the perspective of factual physical significance and the physical true solution is demonstrated as the bottom colored bold dash line in Fig. 7. It is clear that the smaller the rotational angle of the roofing and the larger the support factor of the gangue at the gob, the larger the periodic fractured dimension of the roofing. With the increase of collapsed height of the roofing, the caved gangue gradually fills the gob space, the allowable rotation and settlement of the roofing are reduced and the supporting effect of the gangue at the gob increases. Therefore, the hinged structure of higher overlying rocks normally possesses outstanding fractured block dimensions.

Similarly, when logarithmic relationship exists between the support factor of the gangue at the gob and the mining height of the coal face, by correlating Eq. (8) and Eq. (9), the relationship between the fractured dimensions of the roofing and the mining height of the coal seam is shown in Fig. 8.

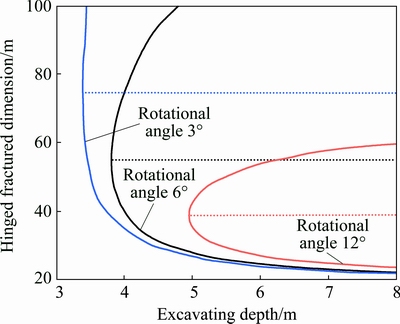
Fig. 8 Relationship between fractured dimensions of roofing and mining depth of coal seam

Similar with the effect of support factor of the gangue at the gob on the fractured dimension of the hinged roofing, it is clear from Fig. 8 that the smaller the rotational angle of the roofing and the mining height of the coal seam are, the larger the periodic fractured dimension of the roofing is. With the reduction of the mining height of the coal seam, the variation of increase rate of the dimensions of the fractured blocks of the roofing is smooth. Within the range of relevant critical excavating height, the dimensions of the fractured blocks of the roofing increase significantly. With the increase of rotational angle of the roofing, the variation gradient of the dimensions of the fractured blocks of the roofing is not obvious and the effect of rotational angle on the fractured block dimensions is not significant.

2) Determination of thickness of hinged roofing structure

According to Eq. (2), the calculating equation of the collapsed height of the roofing at the gob as well as the equations for the calculation of the thickness of combined cantilever beam as well as non-hinged roofing structure, the thickness of hinged roofing can be calculated as

H_g=h_t-H_z-H_f                                             (20)

where H_g is the thickness of the hinged roofing structure at the gob.

3.5 Calculating example of large mining height roofing

Large mining height coal face 8218 at Jinhuagong coal mine in Datong minefield was selected as background and area division was conducted of the roofing structure at the coal face. In order to evaluate the relationship between the support of coal face and surrounding rocks, the support resistance of the coal face was calculated to provide basis.

1) Collapsed height of roofing

According to prior analysis, the collapsed height of the roofing of large mining height coal face at Jinhuagong coal mine met the following relationship:

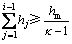                               (21)

where κ is the average residual bulking factor of the fractured blocks of the roofing.

Due to long term compression, the residual bulking factor of the caved gangue at the gob became stabilized. In this occasion, the residual bulking factor of the fractured sandy hard rock roofing was taken as 1.05-1.08 [2]. The condition of determination of the collapsed height of the gob of large mining height coal face can be calculated according to Eq. (21) as

                       (22)

The determination criterion of the caved height of roofing at the gob of Jinhuagong coal mine was acquired as shown in Table 3.

It is clear from Table 3 that the collapsed height of roofing at the gob of large mining height coal face 8218 at Jinhuagong coal mine was approximately 48.8 m.

2) Combined cantilever structure of roofing

The caved gangue at the gob underneath the combined cantilever beam of the roofing became stable and balanced due to the self-weight. The caved gangue remained at initial swell mode and the bulking factor of the gangue was relatively high. The average bulking factor of the caved gangue at the gob at that stage was 1.20 [2-3]. According to Eq. (6), the thickness of the combined cantilever structure of the roofing was calculated as 26 m.

3) Non-hinged structure of roofing

In the condition that logarithmic relationship existed between the support factor of the gangue at the gob and compressive modulus and the mining height of the coal seam, the support factor of the caved gangue at the gob and the compressive modulus with respect to the large mining height coal seam at Jinhuagong coal mine were taken as 0.2 and 0.33 MN, respectively. The component of the non-hinged roofing at the large mining height coal face at Jinhuagong coal mine can be determined according to Eq. (15), as shown in Table 4.

It is clear from Table 4 that the thickness of the non-hinged structure of the roofing at the gob of large mining height coal face at Jinhuagong coal mine was 12.6 m.

Table 3 Determination of collapsed height of roofing

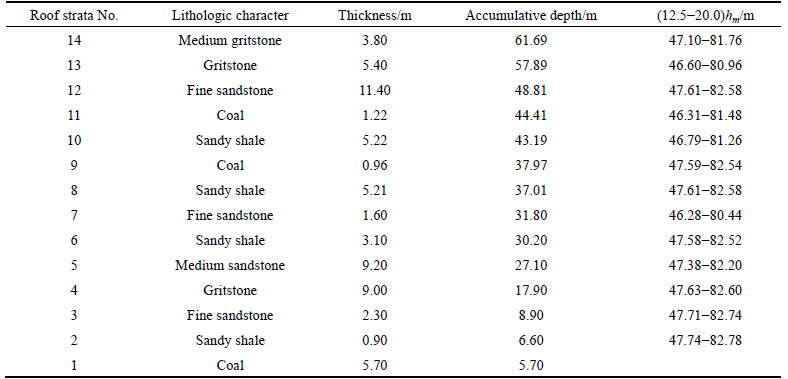
Table 4 Constituents of non-hinged roofing at large mining height coal face

4) Hinged structure of roofing

The thickness of overlying rock hinged roofing structure was calculated according to Eq. (20) as 10 m and the thickness of overlying No.11 rock stratum above the coal seam was 11.4 m. It is clear that hinged structure will form when the roofing fractures under the supporting effect of caved bulking of underneath rock stratum.

4 Calculation of support resistance at large mining height coal face

In the condition of large mining height, the working mode of the support and the supporting quality affect the stability of the combined cantilever structure and the non-hinged roofing structure, and the stability of the later reacts to the support. Due to the existence of the combined cantilever roofing at the coal face and the supporting effect of the caved gangue at the gob on the non-hinged roofing structure, the interacting medium between the support and the hinged roofing structure cannot be simplified as the immediate roof in the conventional mining pressure theory, and the pattern of interaction between the support and surrounding rocks needs to be confirmed. Therefore, according to the characteristics of the roofing structure at large mining height coal face, the model of “support – caved gangue – combined cantilever beam – non-hinged roofing – hinged roofing” system is proposed in this work [16, 21-22], as shown in Fig. 9.

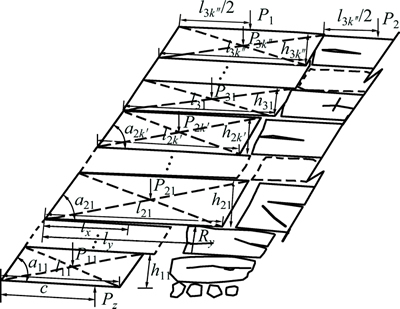
Fig. 9 Model of large mining height roofing system

In order to solve the mechanical model of the roofing system, the effect of combined beam at the roofing on the support at the coal face is first analyzed [16, 21]. It is known that the effect of combined cantilever beam structure on the support resistance depends on the weight, thickness, fractured angle, and fractured dimensions of the roofing sub-layers as well as the location of the action point of the support resistance. Among the abovementioned factors, the thickness and the fractured dimensions of the roofing sub-layers of the combined cantilever beam structure are the key factors. In view of the fact that the height of the combined cantilever beam structure of the roofing of coal face 8218 was 26 m, it was determined that the combined cantilever structure consisted of the 1st to 6th sub-layers above the coal seam, as shown in Table 5.

According to the physical and mechanical parameters of the combined cantilever beam roofing in Table 5, the variation of support resistance at the coal face with the fractured angle of roofing is shown in Fig. 10.

It was measured that the fractured angle of the sandy rock roofing at coal face 8218 was about 85°. With consideration of only combined cantilever beam structure, the support resistance of the coal face was about 12 MN.

Secondly, the loading of support of the coal face under the effect of non-hinged roofing structure was analyzed [16]. Similarly, analysis showed that the non-hinged roofing structure of coal face 8218 consisted of the 7th to 10th sub-layers of the roofing, as shown in Table 6.

Actual measurement and analysis showed that the hinged roofing structure was relatively stable and the fractured angle of non-hinged roofing was 85° to 90°. The support resistance of the coal face under the effect of combined cantilever beam and non-hinged roofing structure was calculated as 12 to 13 MN.

Finally, the effect of hinged roofing structure on the support resistance of the support of the coal face was analyzed [2-3,16]. Prior analysis showed the physical and mechanical characteristics of the 11th sub-layer of the roofing above the coal seam, which was the hinged structure of the roofing of coal face 8218, as given in Table 7.

Table 5 Physical and mechanical characteristics of combined cantilever beam structure of coal face 8218

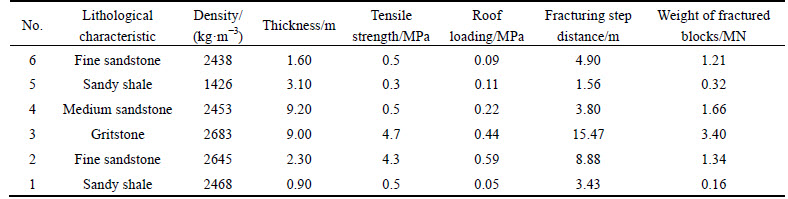
Table 6 Physical and mechanical characteristics of non-hinged roofing structure of roofing of coal face 8218

Table 7 Physical and mechanical characteristics of hinged roofing structure of coal face 8218

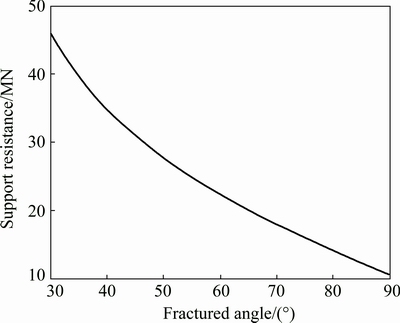
Fig. 10 Relationship between support resistance of support and fractured angle of combined cantilever beam roofing

According to the parameters, it was calculated that the support resistance of the support at coal face 8218 was about 13 to 15 MN. With consideration of the existing condition of instrumentation at the minefield, Model ZZ1300/28/60 support and shield type hydraulic support manufactured by Shanxi Pingyang Industry Machinery Co., Ltd. (the primary technical parameters are listed in Table 8) was selected at Jinhuagong coal mine. With the supplement of the roofing control technique of advanced blasting and pre-cracking [23], the requirements of safe excavation of large mining height coal face were basically met.

5 Conclusions

1) The gob space of large mining height coal face is large. The caving of immediate roof is hard to fill the gob on time and exists in the form of combined cantilever beam structure. While the caved gangue fills the gob space gradually, the compactness of gangue increases and the compressible deformation reduces, leading to the transformation of fractured blocks of roofing from non-hinged rock beam structure to hinged rock beam structure. Finally, the structural mode of “combined cantilever beam – non-hinged roofing – hinged roofing” of the large mining height coal face is formed.

2) With consideration of the supporting effect of gangue at the gob of large mining height coal face, supporting factor of gangue at the gob is introduced to represent the supporting capacity of the caved gangue. The calculating equations of the fractured step distance of roofing in large mining height excavating condition is derived and conventional calculating method of caved height of roofing is corrected and the main factors of the roof caving calculation of large mining height coal face are acquired. The method of determination of the length and height of each structural area of the roofing is theoretically provided.

3) According to the loading condition of the roofing structure of large mining height coal face, the interaction model between the support and roofing structural system is established. With reference to the excavating conditions of large mining height coal face at Jinhuagong coal mine in Datong minefield, the dimensions of structural areas of the roofing of the coal face are theoretically determined and reasonable support resistance of the coal face is provided. By selecting Model ZZ13000/28/60 support and shield type hydraulic support and with procedures of advanced blasting and pre-cracking of roofing, the safe production of large mining height coal face is assured.

Table 8 Primary parameters of Model ZZ13000/28/60 hydraulic support

References

[1] CHEN Yang-guang, QIAN Ming-gao. Strata control around coal face in China [M]. Xuzhou: The Publishing House of China University of Mining and Technology, 1994. (in Chinese)

[2] QIAN Ming-gao, SHI Ping-wu, XU Jia-lin. Mine pressure and strata control [M]. Xuzhou: The Publishing House of China University of Mining and Technology, 2010. (in Chinese)

[3] QIAN Ming-gao, XU Jia-lin. Dominant stratum theory for control of strata movement [M]. The Publishing House of China University of Mining and Technology, 2000. (in Chinese)

[4] WANG Jin-hua. Present status and development tendency of fully mechanized coal mining technology and equipment with high cutting height in China[J]. Coal Science and Technology, 2006, 34(1): 4-7. (in Chinese)

[5] NIN Yu. Techniques and instruments of large mining height mechanized excavation in China [M]. Beijing: Coal Industry Press, 2012. (in Chinese)

[6] XU Yong-qi. Coal mining technology [M]. Xuzhou: The Publishing House of China University of Mining and Technology, 1999. (in Chinese)

[7] HE Fu-lian, QIAN Ming-gao, LIU Chang-you. High production and efficiency support-surrounding rock protection system of coal face [M]. Xuzhou: The Publishing House of China University of Mining and Technology, 1997. (in Chinese)

[8] YASITLI N E, UNVER B. 3D numberical modeling of long wall mining with top-coal caving [J]. International Journal of Rock Mechanics & Mining sciences, 2005, 42: 219-315.

[9] MAO De-bing, KANG Li-jun. Longwall top coal caving mining with higher mining height and its feasibility [J]. Coal Mining Technology, 2003(1): 11-14.

[10] LIU Quan-ming, MAO De-bing. Research on adaptability of full-mechanized caving mining with large [J]. Mining-height Original Research Article Procedia Engineering, 2011, 26: 652-658.

[11] GONG Pei-lin. Theory of surrounding rock control of large mining height stope and its application [M]. Beijing: Coal Industry Press, 2006. (in Chinese)

[12] GONG Pei-lin, JIN Zhong-ming, HAO Hai-jin. Research on stability test for fully mechanized mining support with large mining height [C]//Proceedings of the Second International Symposium on Mining Technology, Jixi, Heilongjiang, China: Science Press, 2001: 246-251.

[13] HUANG Qing-xiang, LIU Wen-gang, TIAN Yin-su. Observation on the law of strata behavior in shallow seam and high mining height face [J]. Ground Pressure and Strata Control, 2003(3): 58-59.

[14] LI Hong-chang. Similar experiment of mining pressure [M]. Xuzhou: The Publishing House of China University of Mining and Technology, 1988. (in Chinese)

[15] WU Feng-feng, YANG Jing-xuan, LIU Chang-you. Determination of the roof caving heights of thick and extra thick coal seams [J]. Journal of China University of Mining & Technology, 2014, 43(5): 765-772. (in Chinese)

[16] WU Feng-feng. Study on the law of roof broken and instability and the control of large mining height fully mechanized mining in thick coal seam [D]. Xuzhou: China University of Mining & Technology, 2014. (in Chinese)

[17] LI Xian-wei. Mechanical properties of rocks [M]. Beijing: Coal Industry Press, 1983. (in Chinese)

[18] LIU Chang-you, CAO Shen-gen. Relationship between the support and surrounding rocks of the stope and the monitoring and control [M]. Xuzhou: The Publishing House of China University of Mining and Technology, 2003. (in Chinese)

[19] SHI Qian, ZENG Ya-wu. Rock mechanics experiment [M]. Wuhan: Wuhan University Press, 2010. (in Chinese)

[20] YANG jing-xuan, LIU Chang-you, YANG Pei-ju. Research on roadside packing technology for end zone of steep inclined coal seam face [J]. Rock and Soil Mechanics, 2014, 35(2): 543-550.

[21] LIU Chang-you, YANG Jing-xuan, YU Bin. Support resistance determination of fully mechanized top-coal caving face in extra thick seam under multi-layered hard strata [J]. Journal of Mining & Safety Engineering, 2015, 32(1): 7-13.

[22] UNVER B, YASITLI N E. Modelling of strata movement with a special reference to caving mechanism in thick seam coal mining [J]. International Journal of Coal Geology, 2006(66): 227-252.

[23] SINGH R. Staggered development of a thick coal seam for full height working in a single lift by the blasting gallery method [J]. International Journal of Rock Mechanics & Mining Sciences, 2004(41): 745-759.

(Edited by DENG Lü-xiang)

Foundation item: Project(51174192) supported by the National Natural Science Foundation of China; Project(BRA2010024) supported by “333” Training Foundation of Jiangsu Province, China; Projects(2011QNB03, 2014ZDPY21, 2014QNB30) supported by the Fundamental Research Funds for the Central Universities, China; Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions, China; Project(2015M581896) supported by China Postdoctoral Science Foundation

Received date: 2015-08-18; Accepted date: 2015-12-15

Corresponding author: LIU Chang-you, PhD; Tel: +86-516-83590002; E-mail: cyliucumt@163.com