DOI: 10.11817/j.issn.1672-7207.2018.02.005
除雾器中细颗粒物湍流扩散模型研究
蔡新剑,袁竹林
(东南大学 能源与环境学院,江苏 南京,210096)
摘要:为了研究细颗粒物在除雾器中的运动扩散规律以提高除雾器细颗粒物脱除效率的计算精度,研究粒径小于15 μm的雾滴在除雾器中的运动。分别采用欧拉法和拉格朗日方法计算气相场和雾滴轨迹;分别耦合连续随机轨道(CRW)模型和离散随机轨道(DRW)模型对不同粒径(3~15 μm)的细颗粒物的脱除效率进行计算,并与实验值进行对比;采用大涡模拟方法(LES)对除雾器中细颗粒物的运动进行进一步对比分析。研究结果表明:2种随机轨道模型能够在一定程度上提高除雾器中细颗粒物脱除效率的计算精度,其对细颗粒物的扩散预测在各向同性的湍流中较准确,而在各向异性湍流中结果并不理想。
关键词:数值模拟;气液两相流;除雾效率;湍流扩散;随机轨道模型
中图分类号:TQ021.4 文献标志码:A 文章编号:1672-7207(2018)02-0290-10
Research on the turbulent particle dispersion model in baffle demisters
CAI Xinjian, YUAN Zhulin
(School of Energy and Environment, Southeast University, Nanjing 210096, China)
Abstract: To research the particle dispersion regularity in eliminators and improve the calculation accuracy of the droplets separation efficiency, the movement of droplets smaller than 15 μm in diameter in baffle demister was studied. The gas phase flow field was determined with Eulerian method and the droplet trajectories were computed by applying the Lagrangian method. Two turbulent dispersion models, i.e., discrete random walk (DRW) model and the continuous random walk (CRW) model, were used to predict the turbulent dispersion of the droplets. The separation efficiencies of the droplets (3 to 15 μm in diameter) were calculated and compared with the experiment results. Large eddy simulation (LES) was also used to predict the motion of droplets for further comparative analysis. The results show that the two turbulent dispersion models can improve the accuracy of the droplets separation efficiency computation. The stochastic trajectory models can predict the particle dispersion in homogeneous isotropic turbulent flows well while they have not good performance in inhomogeneous turbulent flows.
Key words: numerical simulation; gas-liquid flow; demister efficiency; turbulent dispersion; random walk model
除雾器是湿法脱硫(WFGD)[1]系统的重要设备,若其在运行过程中效率降低,则会造成排烟中携带大量雾滴,形成“石膏雨”现象[2]。目前,随着我国PM2.5排放标准愈加严格,提高除雾器对细颗粒物的脱除效率已经迫在眉睫。过去,人们主要通过数值模拟与实验结合的方式对除雾器进行研究。B RKHOLZ等[3-4]对折形板和波纹板除雾器的性能特点进行了测试,其研究结果表明:影响除雾器性能的主要因素包括气流速度、叶片倾斜角、除雾器级数和板间距。VERLAAN[5]研究了液滴粒径在20~90 μm范围内的除雾效率,发现液膜在波纹板上的溢流会造成除雾器叶片捕集液滴能力下降。郝雅洁等[6]利用流体动力学计算方法对湿法脱硫折流板除雾器内气液两相流动进行数值模拟,分析了除雾器叶片间距、板型及流速对不同粒径雾滴的分级除雾效率和总除雾效率的影响,获得了不同粒径雾滴的运动和捕集规律。AL-FULAIJ等[7]针对除雾器在不同气速和不同温度下的性能表现进行模拟研究,并将其与实验数据进行对比,二者结果较吻合。上述研究表明,目前主要通过欧拉-拉格朗日法[8]对除雾器进行数值模拟研究。通过雷诺平均方法(RANS)计算除雾器的流场,并通过耦合曳力模型对雾滴在除雾器中的运动进行统计,可以得出较准确的结果。然而,过去对除雾器的研究主要集中于粒径大于20 μm的雾滴,由于惯性较大,该粒径范围内的雾滴受湍流脉动的影响较小。而对于粒径小于20μm的雾滴,由于其对气相场的跟随性能较好,因此,更容易受到流场中湍流脉动对细颗粒物的扩散作用,但在RANS耦合曳力模型的方法中往往忽略了这一因素。KAVOUSI等[9]对带钩折流板进行研究,其结果表明:不考虑湍流扩散计算雾滴的脱除效率时,3~10 μm粒径雾滴的模拟结果与实验结果偏差较大。因此,在除雾器脱除性能的数值模拟中,如何考虑湍流扩散对细颗粒物的影响以使模拟达到更好的精度,对研究除雾器优化改进以适应国家新的排放标准有着重要意义。本文作者以带钩折流板模型[10](简称为ESFAKHRSAR模型)为模拟对象,采用2种主流的湍流扩散模型,即连续随机轨道(continuous random walk, CRW)模型和离散随机轨道(discrete random walk,DRW)模型[11]来研究雾滴在除雾器中的湍流扩散。气相场的计算采取雷诺应力模型,计算不同粒径(3~15 μm)的雾滴在除雾器中的脱除效率。将所得结果与ESTAKHRSAR模型的实验结果进行对比分析。同时,采用大涡模拟对除雾器内不同位置的雾滴运动特性进行进一步分析。通过比较不同模型条件下雾滴的浓度分布和速度脉动强度,分析2个湍流扩散模型的对雾滴扩散的预测特性和适用范围。
RKHOLZ等[3-4]对折形板和波纹板除雾器的性能特点进行了测试,其研究结果表明:影响除雾器性能的主要因素包括气流速度、叶片倾斜角、除雾器级数和板间距。VERLAAN[5]研究了液滴粒径在20~90 μm范围内的除雾效率,发现液膜在波纹板上的溢流会造成除雾器叶片捕集液滴能力下降。郝雅洁等[6]利用流体动力学计算方法对湿法脱硫折流板除雾器内气液两相流动进行数值模拟,分析了除雾器叶片间距、板型及流速对不同粒径雾滴的分级除雾效率和总除雾效率的影响,获得了不同粒径雾滴的运动和捕集规律。AL-FULAIJ等[7]针对除雾器在不同气速和不同温度下的性能表现进行模拟研究,并将其与实验数据进行对比,二者结果较吻合。上述研究表明,目前主要通过欧拉-拉格朗日法[8]对除雾器进行数值模拟研究。通过雷诺平均方法(RANS)计算除雾器的流场,并通过耦合曳力模型对雾滴在除雾器中的运动进行统计,可以得出较准确的结果。然而,过去对除雾器的研究主要集中于粒径大于20 μm的雾滴,由于惯性较大,该粒径范围内的雾滴受湍流脉动的影响较小。而对于粒径小于20μm的雾滴,由于其对气相场的跟随性能较好,因此,更容易受到流场中湍流脉动对细颗粒物的扩散作用,但在RANS耦合曳力模型的方法中往往忽略了这一因素。KAVOUSI等[9]对带钩折流板进行研究,其结果表明:不考虑湍流扩散计算雾滴的脱除效率时,3~10 μm粒径雾滴的模拟结果与实验结果偏差较大。因此,在除雾器脱除性能的数值模拟中,如何考虑湍流扩散对细颗粒物的影响以使模拟达到更好的精度,对研究除雾器优化改进以适应国家新的排放标准有着重要意义。本文作者以带钩折流板模型[10](简称为ESFAKHRSAR模型)为模拟对象,采用2种主流的湍流扩散模型,即连续随机轨道(continuous random walk, CRW)模型和离散随机轨道(discrete random walk,DRW)模型[11]来研究雾滴在除雾器中的湍流扩散。气相场的计算采取雷诺应力模型,计算不同粒径(3~15 μm)的雾滴在除雾器中的脱除效率。将所得结果与ESTAKHRSAR模型的实验结果进行对比分析。同时,采用大涡模拟对除雾器内不同位置的雾滴运动特性进行进一步分析。通过比较不同模型条件下雾滴的浓度分布和速度脉动强度,分析2个湍流扩散模型的对雾滴扩散的预测特性和适用范围。
1 数学模型
1.1 气相场输运方程
气相场均采用雷诺应力模型(Reynolds-stress model,RSM)进行计算。RSM模型属于高雷诺数模型,与k—ε模型相比,避免了同性的涡黏性假设,同时也需要占用CPU更多的时间和内存。RSM模型适用于复杂的3D流动,能够较好地预测管道中的二次流。RSM模型的基本方程如下:
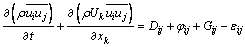 (1)
(1)
式中: 为雷诺应力项;ρ为流体密度;
为雷诺应力项;ρ为流体密度;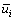 和
和 分别为i和j方向的脉动速度;t为时间;xk为笛卡尔坐标分量;Uk为速度时均分量;Dij为扩散项;φij为压力应变项;Gij为产生项;εij为耗散项。
分别为i和j方向的脉动速度;t为时间;xk为笛卡尔坐标分量;Uk为速度时均分量;Dij为扩散项;φij为压力应变项;Gij为产生项;εij为耗散项。
1.2 拉格朗日路线下离散液滴的控制方程
液滴在除雾器内主要受曳力与重力作用,液滴运动满足牛顿第二定理,其运动方程如下:
 (2)
(2)
Vt=V0+at (3)
 (4)
(4)
式中:mp为液滴的质量;up为液滴的速度;FD和Fg分别为液滴受到的曳力和重力;V0为雾滴初始速度;a为加速度;Vt为液滴在加速度a作用下经历时间t后的速度;s为液滴在t时间内的运动距离。
 (5)
(5)
式中:μ为动力黏度;CD和Re分别为曳力系数和颗粒Reynolds数;u,dp和ρp分别为气流速度、液滴直径和液滴密度。
 (6)
(6)
式中:ρq为气体密度。

1.3 湍流扩散模型
1.3.1 离散随机轨道模型
流场的运动扩散速度ug,通常由时均速度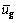 和脉动速度
和脉动速度 组成[12]:
组成[12]:
 (8)
(8)
离散随机轨道模型(DRW)通过随机方法来获得雾滴运动轨迹中的瞬时流场脉动速度。在离散随机轨道模型中,涡的存在通过随机脉动速度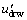 和涡的存在时间τe来描述。随机脉动速度在每一个涡旋的存在时间内维持不变,其值利用高斯分布随机产生:
和涡的存在时间τe来描述。随机脉动速度在每一个涡旋的存在时间内维持不变,其值利用高斯分布随机产生:
 (9)
(9)
式中:ξ为服从高斯分布的随机值。DRW模型中的涡存在时间的定义可以分为随机涡存在时间和恒定涡存在时间2种观点。在恒定涡存在时间的观点中,τe被定义为
 (10)
(10)
式中:TL为拉格朗日时间尺度,可被近似估计为
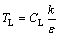 (11)
(11)
而在随机涡存在时间的观点中, 被定义为在TL周围的随机值:
被定义为在TL周围的随机值:
 (12)
(12)
1.3.2 连续随机轨道模型
CRW模型通常建立在郎之万方程[11]的基础上。相比DRW模型,CRW模型通常可以提供更加符合实际情况的湍流颗粒扩散预测。图1所示为DRW模型与CRW模型中脉动速度随时间变化的对比图[13]。
通过朗之万方程定义颗粒轨迹中的脉动速度,标准的郎之万方程在流动边界层范围内按第i个方向可以写成以下形式[14]:
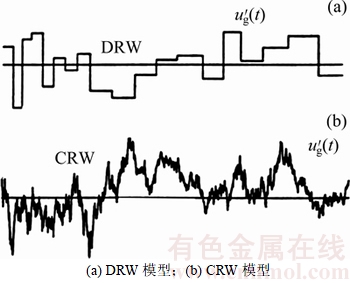
图1 DRW模型与CRW模型脉动速度随时间变化的对比图[13]
Fig. 1 Comparison of the velocity fluctuation time histories for the DRW and CRW models
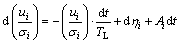 (13)
(13)
式中:ui为流体脉动速度;σi为速度的均方根; dηi为一系列不相干的随机应力项;Ai为平均漂移修正项[11],用来保证惯性较小近似流体的颗粒群可以随时间推移而能够较好地混合。
1.4 大涡模拟数学模型
大涡模拟(LES)的主要原理如下:将湍流分解为可解尺度湍流运动和不可解尺度湍流运动,并且认为大尺度运动几乎包含所有的能量,而小尺度运动主要起能量耗散作用,几乎不受流场边界形状或平均运动的影响,近似认为是各向同性的[15]。对小尺度涡旋采取湍流模型求解而对可解尺度运动则直接进行数值求解。物理空间的滤波过程可表示如下:
 (14)
(14)
式中: 为滤波后的函数;D为滤波空间;G(x) 为滤波函数。上述滤波过程可以选用不同的滤波函数,常用的主要有盒式滤波器、傅氏截断滤波器和高斯滤波器。滤波后的控制方程为
为滤波后的函数;D为滤波空间;G(x) 为滤波函数。上述滤波过程可以选用不同的滤波函数,常用的主要有盒式滤波器、傅氏截断滤波器和高斯滤波器。滤波后的控制方程为
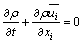 (15)
(15)
 (16)
(16)
其中: 为时间压力;σij为分子黏性引起的应力张量;τij为亚格子应力张量,
为时间压力;σij为分子黏性引起的应力张量;τij为亚格子应力张量,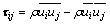 ,需要用亚格子涡模型进行模拟。本文采用Smagorinsky-Lilly亚格子涡模型[16]进行计算。
,需要用亚格子涡模型进行模拟。本文采用Smagorinsky-Lilly亚格子涡模型[16]进行计算。
1.5 雾滴碰撞模型
雾滴在除雾器内运动,会发生相互碰撞、聚并、破裂等现象。由于本研究的雾滴粒径较小,因此,只考虑雾滴与雾滴的聚并现象,而忽略雾滴的破碎现象。
要判断2个雾滴是否碰撞,最简单的办法就是比较其球心距离与半径之和。当球心距离小于其半径之和时,2个雾滴发生碰撞。这种方法需要对空间内任意的2个雾滴进行判断比较,计算效率非常低。本文采用硬球模型,通过计算概率的方式来判断2个雾滴是否发生碰撞,可以有效控制碰撞模拟所需的计算量并在统计上达到相似的结果。
首先由计算机产生1个[0, 1]之间的随机数R,候选雾滴的编号j=int[RN]+1,其中N为所需计算的真实颗粒数量[17]。若R>j/N-pij,则满足雾滴i与雾滴j在Δt内发生碰撞的要求。
雾滴i和j发生碰撞的概率pij计算公式如下:
pij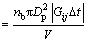 (17)
(17)
式中:Dp为雾滴的直径;Gij为雾滴i与j的相对速度,Gij=Vi-Vj;nb为样本颗粒与真实颗粒数目的比值,nb=n/N;V为流场网格所占的空间体积。
碰撞后2个雾滴融合成1个新的雾滴,其质量m与速度v遵循质量守恒定律与动能守恒定律。
m=mi+mj (18)
mv=mivi +mjvj (19)
2 数值计算与分析
2.1 计算条件
本文选取文献[10]中折流板模型进行模拟计算,如图2所示。将所得的实验数据与文献[10]中实验数据进行对比分析。图3所示为该折流板的物理模型示意图。其中角度α为45°,折角长度λ为118.5 mm,管道垂直厚度S为25.0 mm。

图2 计算采用的折流板三维模型
Fig. 2 Three-dimensional model of baffle demisters for calculation

图3 除雾器几何尺寸
Fig. 3 Vane demister geometry
该折流板除雾器在3个拐角的位置增加了3个直角沟板,以提高对细颗粒物的脱除效率,其位置如图4所示。直角勾板的具体尺寸包含3个参数:弯折角θ、高度A和长度B。本文采取的尺寸方案为:高度A为流道宽度的50%,长度B为流道宽度的34%,弯折角度θ被设定为90°。

图4 流道几何参数
Fig. 4 Drainage channel geometry parameters
本文采用六面体结构网格对模型进行网格划分,并对靠近壁面的区域采取边界层网格加密,如图5所示。经过一定的网格数量无关性测试,RSM模型最终采取的网格总数量大约为23万,大涡模拟要求网格尺寸处于惯性子区尺度范围内,对网格要求较高,因此,并未采用与RSM模型相同的网格划分。其最终采取的方案网格数量约为150万,边界层内首层网格高度y+为0.01 mm,网格高度递增比例约为1.2,进一步提高网格密度。计算结果的变化小于3%。

图5 板计算网格
Fig. 5 Vane computational grids
图6所示为在3种气速下,采取2种不同的网格划分方案的LES模型计算得出的压降与RSM模型以及文献[10]中同一模型的结果对比。图中d/D为非壁面区域网格的尺寸与流道宽度的比值,其中1/100为本文最终选定的网格方案。由图6可知:LES(d/D= 1/100)与RSM模型得出的压降和文献[10]中的结果基本一致;而当采用更稀疏的网格(d/D=1/25)时,其压降略低于其他3种方案的压降,同时有着更少的流场涡旋。

图6 不同网格模型条件下的压降对比
Fig. 6 Comparison of pressure drop in different mesh conditions
由于网格数量不同,LES模型的计算时长要远长于RSM模型的计算时长。在同样设定时间步长为1×10-4 s,运行5×103步的条件下,RSM模型需要大约18h完成计算,而LES模型则需要70 h左右。
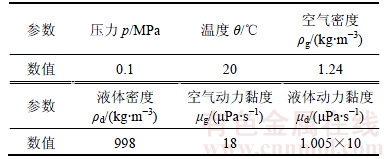
计算所用的环境物性参数如表1所示。计算的入口条件按照文献[10]中测定的湿度将入口雾滴的质量分数设定为9%,流速为3~5 m/s。雾滴的粒径范围为3~15μm,不同粒径的雾滴数量比例服从R-R分布。
表1 两相流动的物性参数
Table 1 Physical property parameters of the two phase flow
2.2 计算结果与分析
2.2.1 不同模型除雾效率对比分析
分别采用CRW模型、DRW模型和None模型(即不采用湍流扩散模型)对该折流板除雾器内的雾滴运动进行模拟计算,粒径除雾效率为该粒径壁面吸收的雾滴数量除以进入除雾器的雾滴数量。
图7所示为在3种入口气速条件下,3种不同的计算条件下所得出的不同粒径雾滴的在折流板内的脱除效率与实验数据的对比。由图7可知:在不同的计算条件下,整体雾滴的脱除效率随粒径的增大而增大,当粒径为10 μm时,脱除效率达到99.9%。

图7 不同模型的除雾效率与实验数据对比
Fig. 7 Comparisons of demisting efficiency of experiment model and simulation models with different methods
而对10 μm以下粒径的雾滴,不同计算条件下所得出的除雾效率均不相同。无论是在哪种气速下,不采用湍流扩散模型所得出的脱除效率均明显低于采取湍流扩散模型计算结果和实验结果。由此可见,由于缺乏对雾滴随湍流脉动扩散的考虑,低于10 μm粒径的雾滴计算出的脱除效率往往小于实际的脱除效率。分析其原因,由于惯性的影响,粒径越小的雾滴跟随气流的松弛时间越短,气流跟随性越好,受到湍流脉动的影响也越明显。因此,缺乏湍流扩散的考虑造成计算误差随着雾滴粒径的减小而增大。
相比于None模型,CRW模型与DRW模型的计算结果与实验结果更吻合。在雾滴粒径约6 μm以下,CRW模型的计算结果整体低于实验结果,而DRW模型的计算结果则高于实验结果;在雾滴粒径7~10 μm范围内,2个模型结果具有较高的一致性,均略低于实验结果。
2.2.2 大涡模型计算结果对比分析
采用大涡模拟对除雾器流场进行非稳态计算。相比于雷诺平均方法,由于大涡模拟保留了流场中的涡旋和速度脉动信息,可以在没有额外扩散模型的条件下体现出湍流场速度脉动对雾滴的扩散作用。为验证大涡模拟结果的准确性,本文同样采取3种气速条件对雾滴的脱除效率进行计算。
图8所示为在3种气速下采用LES模型计算雾滴的脱除效率与实验结果的对比。由图8可知:计算结果与实验结果的吻合度非常高。为更加准确地比较不同模型的优劣,本文将模拟结果与实验结果中不同粒径的最大误差和平均误差进行统计,如表2所示。由表2可知:LES模型误差分析结果均明显优于DRW模型,CRW模型和None模型的结果。这从一定程度上可以说明LES模型对除雾器流场的湍流脉动还原较准确。
为进一步对比不同计算条件下雾滴的扩散,本文选取粒径为3 μm的雾滴在某一时刻除雾器中的位置分布进行对比,如图9所示。由图9可知:在没有考虑湍流扩散的作用时,雾滴运动的轨迹较整齐,雾滴群的边缘与周围有着明显的分界线;同时,由于雾滴仅受到气相场曳力作用,在拐角处低速区有着明显的雾滴无法进入的死区。相比而言,加入湍流扩散模型后,雾滴的在空间中运动的分布范围更大,甚至能进入速度较低的边角区域,雾滴群轨迹范围没有明显的边界存在。None模型、DRW模型和CRW模型均存在着大多数雾滴分布在流速较高的主流区的现象,而在LES模型的条件下,雾滴较为均匀地弥散在整个流道内,其扩散范围与采取RANS方法下的结果差别很大。
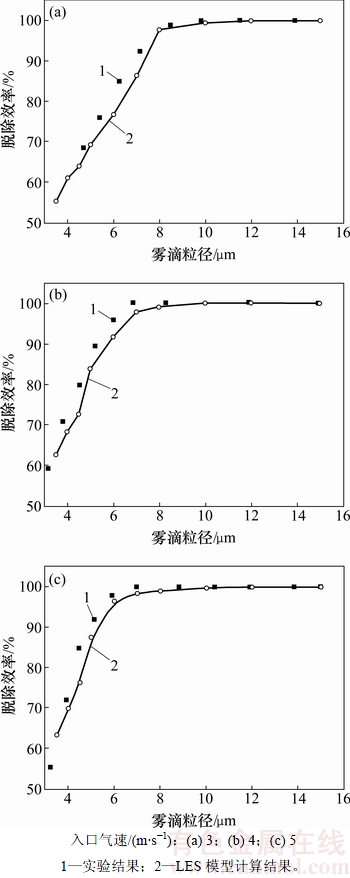
图8 LES模型除雾效率与实验结果对比
Fig. 8 Comparison of demisting efficiency of experiment and simulation with LES model
表2 不同模型除雾效率的误差分析
Table 2 Error analysis of different models


图9 不同模型下雾滴在除雾器中的位置分布
Fig. 9 Position distribution of droplets in demister under different models
为进一步探究造成以上现象的原因,本文选取LES模型和RSM模型所计算流场的速度云图和涡量分布云图进行对比。
由图10可知:在2种不同的湍流模型下,除雾器的入口段和第1段流量和涡量云图分布基本一致。分歧出现在第一段末尾处勾板以后的位置。由于勾板的阻滞作用和流体本身惯性的影响,流场在勾板的正后方拐角内侧形成了一道长长的低速区,空气流量集中于拐角靠外侧的部分并形成高速区。整个流道因此形成流速一边高一边低的速度梯度。RANS方法由于有着较大的涡黏性,即使在非稳态计算下,流场随时间也几乎不发生变化,流道内的流线几乎与流道方向平行,其垂直于流道的速度分量很小,如同层流一般。因此,雾滴在流场中运动时,由于惯性的作用位置大多集中于一边的高速流域,很少有雾滴能横向扩散到低速区域。

图10 RSM和LES模型下的流场流速、涡量比较
Fig. 10 Predicted velocity and vortex contours at eliminator with RSM and LES approaches
相比之下,在大涡模拟条件下,流场拐角的勾板后面产生连续涡街。涡街脱落前进的轨迹覆盖主流高速区域的边缘和整个低速区,形成强烈的流场扰动。当雾滴在其中运动时,由于大尺度涡旋的带动,高流速区域边缘的雾滴不断地被携带到另一侧的低流速回流区,从而整体形成强烈的垂直于流道方向的扩散,使雾滴弥散在整个流道范围内。
2.2.3 雾滴扩散特性统计分析
为对除雾器中不同流场状态下湍流模型的扩散特性进行进一步量化分析,选取前2段的中间截面,对经过的雾滴位置和速度信息进行统计分析,截面位置如图11所示。

图11 截面C和D位置
Fig. 11 Positions of face C and D
根据前面的流场计算结果,截面C代表除雾器中流场较为均匀的各项同性的湍流位置,而截面D则代表各向异性湍流的位置。将截面按速度梯度最大方向划分为等分的10个区域(分别编号1~10),分别统计相同时间内经过截面的雾滴速度方差和雾滴数量分布。入口速度取4 m/s,选取粒径分别为3和7 μm的雾滴。
图12~13所示分别为C截面的雾滴统计结果。粒径为3 μm和7 μm时,在C位置DRW模型和CRW模型下雾滴的数量分布与速度方差均与大涡模拟的结果基本一致。这与文献[18]中采用LES和RANS方法模拟折流板雾滴扩散研究中的折流板相似位置的结果相符合。
图14~15所示分别为D截面的雾滴统计结果。由图12~15可知:3种计算条件下雾滴数量分布有着较大的差别。在大涡模拟流场下,同一位置雾滴的速度方差远远高于DRW模型与CRW模型的方差(见图15)。这说明在D位置2个随机模型模拟出的速度脉动强度跟实际值相差较大,从而导致流场内雾滴弥散区域存在很大差别。
综合上面2个截面雾滴运动的统计结果可知: CRW与DRW模型可以较好地模拟各向同性湍流中的小尺度涡旋的速度脉动,但无法模拟各向异性湍流中大尺度涡旋引起的雾滴脉动扩散,从而会造成较大的计算误差。CRW模型产生的雾滴脉动强度分布较为均匀连续,而DRW模型产生的雾滴脉动强度具有较强的波动跳跃性,这是由于它们产生随机速度的机理不同。

图12 不同模型下C截面不同区域的雾滴数占比
Fig. 12 Quantity distribution of droplets through Face C with different models
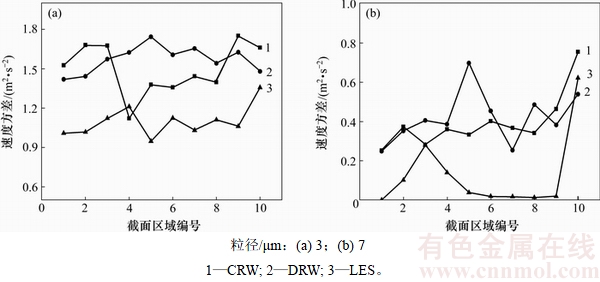
图13 不同模型下C截面通过雾滴的速度方差
Fig. 13 Velocity variance of droplets through Face C with different models

图14 不同模型下雾滴在D截面不同区域的雾滴数占比
Fig. 14 Quantity distribution of droplets through Face D with different models
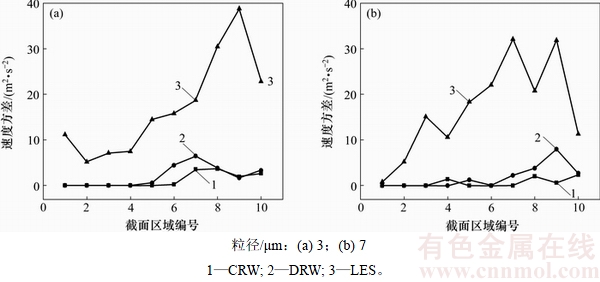
图15 不同模型下D截面通过雾滴的速度方差
Fig. 15 Velocity variance of droplets through face D with different models
3 结论
1) 传统的RANS流场结合曳力模型的方法由于没有考虑湍流扩散的影响,计算得出雾滴的脱除效率整体低于实验值,雾滴的粒径越小,产生的偏差越大。
2) 大涡模拟可以有效地预测流场的脉动和涡旋分布,利用LES模型计算流场并与雾滴相进行耦合计算,其得出的脱除效率与实验值偏差很小。
3) 相比于None模型,采用CRW和DRW模型预测雾滴在除雾器中的湍流扩散,可以有效地提高小粒径(<10 μm)雾滴的脱除效率计算的准确度。2种随机轨道模型在各向同性湍流中对雾滴的速度和脉动预测较准确,而在各向异性湍流中其结果并不理想。
4) CRW模型在相同条件下计算得出的雾滴脱除效率比DRW模型的低,其产生的速度脉动强度在空间中的分布较为连续、均匀,而DRW模型产生的速度脉动则具有一定的波动跳跃性。
5) 对粒径较小(<15 μm)的细颗粒物进行数值模拟时,有必要考虑湍流扩散的作用。LES方法准确性高于RANS方法,但是对计算能力要求较高,花费时间较长。
参考文献:
[1] 杨林军, 颜金培, 沈湘林. 蒸汽相变促进燃烧源PM2.5凝并长大的研究现状及展望[J]. 现代化工, 2005, 25(11): 22-26.
YANG Linjun, YAN Jinpei, SHEN Xianglin. Research status and prospect of vapor phase transformation to promote PM2.5 condensation and growth of combustion sourse[J]. Modern Chemical Industry, 2005, 25(11): 22-26.
[2] 曹作旺, 李云涛. 燃煤电厂湿式电除尘技术[J]. 科技创新与应用, 2014(19): 47-48.
CAO Zuowang, LI Yuntao. wet electric dust removal technology in coal fired power plant[J]. Technology Innovation and Application, 2014(19): 47-48.
[3] B RKHOLZ A. Droplet Separation[M]. New York: VCH Publishers, 1989: 75-79.
RKHOLZ A. Droplet Separation[M]. New York: VCH Publishers, 1989: 75-79.
[4] USHIKI K, NISHIZAWA E, BENIKO H, et al. Performance of a droplet separator with multistage rows of flat blades[J]. Journal of Chemical Engineering of Japan, 1982, 15(4): 292-298.
[5] VERLAAN C C J. Performance of Novel Mist Eliminators[D]. Mekelweg, Nederland: Delft University of Technology, 1991: 152-153.
[6] 郝雅洁, 刘嘉宇, 袁竹林, 等. 除雾器内雾滴运动特性与除雾效率[J]. 化工学报, 2014, 12(12): 4669-4677.
HAO Yajie, LIU Jiayu, YUAN Zhulin, et al. Movement characteristics of droplets and demisting efficiency of mist eliminator[J]. Journal of Chemical Industry and Engineering, 2014, 12(12): 4669-4677.
[7] AL-FULAIJ H, CIPOLLINA A, GIORGIO M, et al. Eulerian– lagrangian modeling and computational fluid dynamics simulation of wire mesh demisters in msf plants[J]. Desalination, 2016, 385(7): 148-157.
[8] YUAN Zhulin. Gas-Solid Two-Phase Flow and Numerical Simulation [M]. Nanjing: Southeast University Press, 2012: 81-92.
[9] KAVOUSI F, BEHJAT Y, SHAHHOSSEINI S. Optimal design of drainage channel geometry parameters in vane demister liquid–gas separators[J]. Chemical Engineering Research & Design, 2013, 91(7): 1212-1222.
[10] ESTAKHRSAR M H H, RAFEE R. Effects of wavelength and number of bends on the performance of zigzag demisters with drainage channels[J]. Applied Mathematical Modelling, 2015, 40(2): 685-699.
[11]  A, ARCEN B. Prediction of a particle-laden turbulent channel flow: Examination of two classes of stochastic dispersion models[J]. International Journal of Multiphase Flow, 2014, 60(2): 1-10.
A, ARCEN B. Prediction of a particle-laden turbulent channel flow: Examination of two classes of stochastic dispersion models[J]. International Journal of Multiphase Flow, 2014, 60(2): 1-10.
[12] RYBALKO M, LOTH E, LANKFORD D. A Lagrangian particle random walk model for hybrid RANS/LES turbulent flows[J]. Powder Technology, 2012, 221(221): 105-113.
[13] MACINNES J M, BRACCO F V. Stochastic particle dispersion modeling and the tracer-particle limit[J]. Physics of Fluids A, 1992, 4(12): 2809-2824.
[14] DEHBI A. Validation against DNS statistics of the normalized Langevin model for particle transport in turbulent channel flows[J]. Powder Technology, 2010, 200(1): 60-68.
[15] 张晓龙, 张楠, 吴宝山. 壁面涡旋结构与湍流脉动压力的大涡模拟研究[J]. 船舶力学, 2014, 18(8): 871-881.
ZHANG Xiaolong, ZHANG Nan, Wu Baoshan. Computation of tunnel wall pressure fluctuations using large eddy simulation[J]. Journal of Ship Mechanics, 2014, 18(8): 871-881.
[16] SMAGORINSKY J. General circulation experiments with primitive equations[J]. Monthly Weather Review, 1963, 91(3): 99-164.
[17] 樊水冲, 杨学忠, 郭 勇. 波纹板除雾器流场与效率的数值计算[J]. 炼油与化工, 2006, 17(2): 5-10.
FAN Shuichong, YANG Xuezhong, GUO Yong. Numerical computation on flow filed and efficiency of wave-plate[J]. Refining and Chemical Industry, 2006, 17(2): 5-10.
[18] RUIZ J, KAISER A S, ZAMORA B, et al. CFD analysis of drift eliminators using RANS and LES turbulent models[J]. Applied Thermal Engineering, 2016, 105: 979-987.
(编辑 伍锦花)
收稿日期:2017-03-30;修回日期:2017-05-29
基金项目(Foundation item):国家自然科学基金资助项目(51576046);江苏省科技计划项目(BY2015070-15)(Project(51576046) supported by the National Natural Science Foundation of China; Project (BY2015070-15) supported by the Scientific Research Project of Jiangsu Province)
通信作者:袁竹林,博士,教授,从事于气固两相流相关研究;E-mail: zlyuan@seu.edu.cn