DOI: 10.11817/j.issn.1672-7207.2017.06.001

富硼渣MgO-B₂O₃-SiO₂-FeO体系表面张力计算

许继芳¹，陈栋¹，翁文凭¹，盛敏奇¹，张捷宇²，吕凡¹

(1. 苏州大学 沙钢钢铁学院，江苏 苏州，215021；

2. 上海大学 省部共建高品质特殊钢冶金与制备国家重点实验室，上海，200072)

摘要：基于熔渣结构离子与分子共存理论和Butler方程建立MgO-B₂O₃-SiO₂-FeO体系表面张力计算模型，计算该体系及其子体系的表面张力，考察熔渣组元和温度对表面张力的影响。研究结果表明：本模型计算的相关体系熔渣表面张力与文献实验值吻合较好，模型平均相对误差为11.85%。含B₂O₃体系熔渣中，B₂O₃组元能够显著降低熔渣表面张力，纯氧化物表面张力与形成氧化物的阳离子静电势及氧化物中离子键分数有关。MgO-B₂O₃-SiO₂-FeO体系表面张力随B₂O₃含量增加和温度升高而显著降低，随着MgO/SiO₂质量比的增加而逐渐增大；当B₂O₃质量分数为17%~19%时，表面张力随FeO含量的变化规律发生改变，当B₂O₃含量较低时，熔渣表面张力随着FeO含量的增加而增大，当B₂O₃含量较高时，表面张力随着FeO含量的增加而降低。

关键词：MgO-B₂O₃-SiO₂-FeO熔渣；B₂O₃含量；表面张力；共存理论；计算模型

中图分类号：TF01             文献标志码：A         文章编号：1672-7207(2017)06-1413-07

Evaluation of surface tension for MgO-B₂O₃-SiO₂-FeO boron-rich slag

XU Jifang¹, CHEN Dong¹, WENG Wenping¹, SHENG Minqi¹, ZHANG Jieyu², L Fan¹

(1. Shagang School of Iron and Steel, Soochow University, Suzhou 215021, China;

2. State Key Laboratory of Advanced Special Steel, Shanghai University, Shanghai 200072, China)

Abstract: Based on the coexistence theory of ions and molecules of molten melt structure and Butler’s equation, a thermodynamic model was developed to establish the surface tension of MgO-B₂O₃-SiO₂-FeO system and its sub-system. The relationship between the composition and temperature and surface tension of molten slag was investigated. The results indicate that the calculated values for related systems show good agreements with the literature data, and the average error is about 11.85%. The surface tension of molten slag decreases with increasing the B₂O₃ content significantly in molten slag binary system. The surface tension value of pure oxide is related to the electrostatic potential of cations and the ion bond percentage in oxide. The surface tension in MgO-B₂O₃-SiO₂-FeO system decreases significantly with increasing temperature and the B₂O₃ content, and increases with increasing the mass ratio of MgO to SiO₂. While the B₂O₃ content is 17%-19%, the trends that surface tension varied with the FeO content, are changed. When the B₂O₃ content is low, surface tension of slag increases with the increase of the FeO content; when the B₂O₃ content is high, the surface tension decreases with the increase of the FeO content.

Key words: MgO-B₂O₃-SiO₂-FeO slag; B₂O₃ content; surface tension; coexistence theory; calculating model

我国硼铁矿资源丰富，硼及其化合物应用领域广泛，开发利用硼铁矿资源具有重要价值。富硼渣提硼是硼铁矿“火法”路线综合利用的关键环节^[1]，富硼渣主要由B₂O₃，MgO，SiO₂和少量CaO和Al₂O₃组成，可看作MgO-B₂O₃-SiO₂准三元系^[2]。富硼渣熔体物性对铁硼分离提取具有显著影响，其中表面张力对渣金反应、渣铁分离等过程具有决定作用^[3]。硼铁矿高炉铁硼分离生产含硼生铁及富硼渣过程中，少量Fe进入熔渣中，渣中氧化铁属于表面非活性组分，可提高熔渣的表面张力，但渣中氧化铁能在钢液中存在，使熔渣与钢液之间界面结构趋于一致，降低表面质点之间的失配，从而降低渣金界面张力，因此有必要开展含FeO多元渣系表面张力研究。目前有文献测量了含硼渣的表面张力^[4-10]，但主要研究含B₂O₃连铸保护渣^[6-7]和硼酸盐玻璃体系^[8-10]，MgO-B₂O₃-SiO₂准三元系的富硼渣体系熔渣表面张力研究较少。崔传孟等^[5]测量了低CaO含量和Al₂O₃含量的MgO-B₂O₃-SiO₂- 6CaO-8Al₂O₃体系熔渣表面张力，研究了熔渣成分对表面张力的影响。鉴于熔渣表面张力测定的实验难度和成本，利用模型对多元熔渣体系表面张力进行计算和预测是解决含硼渣基础物性数据缺乏的有效途径。基于表面张力Butler方程，成国光等^[11]依据熔渣结构离子和分子共存理论中结构的合理假设，提出了一个热力学模型计算熔渣的表面张力，该模型简单且适用性强，在多组元熔渣体系表面张力计算中得到广泛验证和推广^[12-13]。因此，本文作者基于含B₂O₃熔渣结构的离子与分子共存理论和熔体表面张力Butler方程，建立MgO-B₂O₃-SiO₂-FeO体系表面张力的计算模型，并将计算结果与对应的实验测量值进行对比，以验证模型的准确性；在此基础上，计算1 873 K下MgO-B₂O₃-SiO₂-FeO体系及其子体系的熔渣表面张力，研究熔渣成分与表面张力的关系，探索FeO含量对富硼渣表面张力的影响，以期为富硼渣调控、优化提供参考。

1  MgO-B₂O₃-SiO₂-FeO体系熔渣结构单元的确定

熔渣结构单元中离子、简单分子和复杂分子的确定是熔渣结构离子与分子共存理论的关键环节。B₂O₃-MgO二元体系相图中确定存在3MgO·B₂O₃和2MgO·B₂O₃复杂化合物，但对是否存在MgO·B₂O₃以及MgO·2B₂O₃物相是否稳定存在尚存争议^[14-16]，本研究确定高温下稳定存在的主要物相为3MgO·B₂O₃和2MgO·B₂O₃。B₂O₃-FeO二元体系相图中确定的主要物相为3FeO·B₂O₃，2FeO·B₂O₃和FeO·B₂O₃^[4]。MgO-SiO₂二元体系相图中确定的主要物相为2MgO·SiO₂和MgO·SiO₂^[4]。SiO₂-FeO二元体系相图中确定的主要物相为2FeO·SiO₂和FeO·SiO₂^[4]。B₂O₃-SiO₂和MgO-FeO二元体系相图中无复杂化合物^[4]。MgO-B₂O₃-SiO₂三元体系相图和MgO-SiO₂-FeO三元体系相图中不存在三元复杂化合物^{[4, 17-18]}。MgO-B₂O₃-FeO三元体系、B₂O₃-SiO₂-FeO体系和MgO-B₂O₃-SiO₂-FeO四元体系相图未有相关报道。综上所述，本研究确定MgO-B₂O₃-SiO₂-FeO体系熔渣中存在的结构单元包括Mg²⁺，Fe²⁺和O^2- 3种离子，B₂O₃和SiO₂ 2种简单分子以及上述9种复杂化合物分子。

2  MgO-B₂O₃-SiO₂-FeO体系熔渣表面张力模型的建立

Butler方程通过化学势和表面能推出表面张力与热力学的关系，建立熔体表面张力计算模型。在本文表面张力计算模型中，主要假设如下：1) 熔渣表面相与体相都遵守熔渣结构离子与分子共存理论，即组元结构都由离子、分子和复合分子组成，熔渣表面相和体相中形成的复合分子都遵守反应动力学平衡和质量守恒；2) 熔渣体相和表面相中各组元的质量作用浓度和熔渣表面张力符合Butler方程：

           (1)

式中：σ_i^pure为纯组元i(i=MgO，B₂O₃，SiO₂和FeO)的表面张力；A_i为纯组元i的摩尔表面积(A_i=L·N₀^1/3·V_i^2/3，其中L为校正因子，熔渣中氧化物混合物通常设为1.091；N₀为阿伏伽德罗常数，V_i为组元i的摩尔体积)；R和T分别为摩尔气体常数和热力学温度；N_i^Surf和N_i^Bulk分别为组元i在表面和体内的质量作用浓度。

据熔渣离子与分子共存理论假设^[19]及上述分析可确定MgO-B₂O₃-SiO₂-FeO熔渣中存在的结构单元。对于MgO-B₂O₃-SiO₂-FeO体系，定义熔渣中成分分别为：b₁=∑n_MgO，b₂=∑n_FeO，a₁=∑n_B2O3和a₂=∑n_SiO2。结构组元质量作用浓度表示为：N₁=n_MgO，N₂=n_B2O3，N₃=n_SiO2，N₄=n_FeO，N₅=n_3MgO·B2O3，N₆=n_2MgO·B2O3，N₇=n_2MgO·SiO2，N₈=n_MgO·SiO2，N₉=n_3FeO·B2O3，N₁₀=n_2FeO·B2O3，N₁₁=n_FeO·B2O3，N₁₂=n_2FeO·SiO2和N₁₃=n_FeO·SiO2。所有结构组元总平衡摩尔数可表示为∑n_i。MgO-B₂O₃-SiO₂-FeO渣系中各组分的作用浓度表达式为：N₁=2n₁/∑n_i，N₂=n₂/∑n_i，N₃=n₃/∑n_i，N₄=2n₄/∑n_i。在1 623~1 873 K范围内，渣系中各组元形成复杂分子的反应式及其达到平衡时的标准Gibbs自由能(以纯物质为标准态)和质量作用浓度表达式如表1所示，所有反应的平衡常数可通过关系式进行计算。

表1  MgO-B₂O₃-SiO₂-FeO渣系中复杂分子的化学反应及标准Gibbs自由能和质量作用浓度的表达式

Table 1  Formulas of mass action concentrations, standard Gibbs free energies and chemical reactions of complex molecules in MgO-B₂O₃-SiO₂-FeO slag system

MgO-B₂O₃-SiO₂-FeO体系中质量平衡公式如下：

b₁=Sn_i·(0.5N₁+3N₅+2N₆+2N₇+N₈)       (2)

b₂=Sn_i·(0.5N₄+3N₉+2N₁₀+N₁₁+2N₁₂+N₁₃)    (3)

a₁=Sn_i·(N₂+N₅+N₆+N₉+N₁₀+N₁₁)        (4)

a₂=Sn_i·(N₃+N₇+N₈+N₁₂+N₁₃)         (5)

N₁+N₂+N₃+N₄+…+N₁₃=1          (6)

表1和式(2)~(6)是建立的计算MgO-B₂O₃-SiO₂- FeO体系中结构组元和离子对的作用浓度N_i的控制方程，其中N₅~N₁₃可由N₁~N₄表示。在一定温度条件下，熔渣成分代入该方程组，经过线性化处理后，采用迭代法即可计算出所有结构组元和离子对的作用浓度。

对于MgO-B₂O₃-SiO₂-FeO体系，根据Bulter方程，其表面张力可分别表示为：

          (7)

          (8)

          (9)

         (10)

通过本文模型计算出MgO-B₂O₃-SiO₂-FeO体系表面张力，首先，基于熔渣结构离子与分子共存理论，通过熔渣成分的摩尔分数和熔渣结构单元形成复合分子的化学平衡计算得出N_i^Bulk。然后，根据已知量N_i^Surf，σ_i^pure和A_i，利用方程(6)~(8)可计算出σ和N_i^Surf。MgO-B₂O₃-SiO₂-FeO体系中σ_i^pure和A_i见表2和表3^[20-21]。

表2  纯组元摩尔体积和表面张力与温度的关系

Table 2  Temperature dependence of surface tension and molar volume of pure components

3  计算结果及讨论

3.1  表面张力的计算值与文献实测值对比

为了验证本模型计算结果的可靠性，需将计算结果与实验数据进行对比。但MgO-B₂O₃-SiO₂-FeO体系表面张力实验数据未见报道，只有相关的MgO-SiO₂体系、SiO₂-FeO体系、MgO-SiO₂-FeO体系^[4]及低CaO含量和Al₂O₃含量的MgO-B₂O₃-SiO₂-6CaO-8Al₂O₃体系^[5]的表面张力实验数据的报道。本文计算了上述体系的表面张力计算值，并与文献实验数据进行了对比，对比结果如图1所示。本模型总的平均相对误差约为11.85 %，熔渣表面张力的实验误差为5%~10%，因此，本模型计算的熔渣表面张力与实验值基本吻合。其中MgO-SiO₂体系的计算值与实验值较一致，MgO-B₂O₃-SiO₂-6CaO-8Al₂O₃体系的计算值比实验值略大，这可能与本体系模型中未考虑CaO和Al₂O₃组元对表面张力的影响，而仅仅将CaO和Al₂O₃含量归入MgO含量有关。由于CaO和Al₂O₃纯物质的表面张力偏大，因此，MgO-B₂O₃-SiO₂熔渣中加入CaO和Al₂O₃组元将提高熔渣的表面张力^[4]。SiO₂-FeO体系和MgO-SiO₂-FeO体系的表面张力计算值与实验值也有偏差，这可能与模型选取的FeO纯物质表面张力有关，本模型FeO纯物质表面张力文献值中未考虑熔渣气氛对渣中Fe²⁺/Fe³⁺摩尔比的影响，而Fe₂O₃组分含量将影响熔渣表面张力。因此，模型参数的选择和准确的熔渣组元结构决定模型计算结果精度。

图1  MgO-B₂O₃-SiO₂-FeO体系相关渣系表面张力计算值与实验数据的比较

Fig. 1  Comparison between calculated values with measured values for MgO-B₂O₃-SiO₂-FeO related system

3.2  含B₂O₃二元体系熔渣表面张力变化

采用本模型计算1 873 K下含B₂O₃二元体系熔渣表面张力，考察B₂O₃含量对熔渣表面张力的影响。MgO-B₂O₃体系中，1 873 K时，在富MgO区(B₂O₃质量分数＜28%)，存在MgO相和液相的固液两相区(液相II+MgO)，在富B₂O₃区(B₂O₃质量分数＞70%)存在两液相不互溶区(液相I+液相II)，且该区处于亚稳态，有关该亚稳态区，其边界、体系热力学性质等研究尚不清楚，因此本文虽然计算了MgO-B₂O₃渣系全浓度范围内的表面张力变化情况，但仅B₂O₃质量分数在28%~70%范围内熔渣处于单一液相区(液相II)^[22]。FeO-B₂O₃体系中，在富B₂O₃区同样存在两液相不互溶区。1 873 K时，在富FeO区(B₂O₃质量分数＜13%)，存在FeO相和液相的固液两相区(液相II+FeO)，在富B₂O₃区(B₂O₃质量分数＞69%)存在两液相不互溶区(液相I+液相II)，且该区处于亚稳态，因此本文虽然计算了FeO-B₂O₃渣系全浓度范围内的表面张力变化情况，但仅B₂O₃质量分数在13%~69%范围内熔渣处于单一液相区(液相II)^[4]；B₂O₃-SiO₂体系中，熔渣液相区(液相)范围比较大，仅富SiO₂区(B₂O₃质量分数＜3%)存在方英石相和液相的固液两相区(液相+方英石相) ^[4]。含B₂O₃二元体系熔渣表面张力计算结果如图2所示。结果表明，作为表面活性物质，B₂O₃组元能够显著降低熔渣表面张力。熔渣表面张力随着B₂O₃含量的增加而显著降低。MgO-B₂O₃体系和FeO-B₂O₃体系中，随着酸性氧化物B₂O₃含量的增加，熔渣中阴离子结构将复杂化，聚合程度提高，对阳离子的静电引力减弱，从而降低了熔渣体系的表面张力^[23]。B₂O₃-SiO₂体系，B₂O₃对表面张力的降低作用，可能与硼氧阴离子团与硅氧阴离子团之间的差异有关^[5]。

图2  1 873 K下含B₂O₃二元熔渣表面张力

Fig. 2  Surface tension of molten binary system containing B₂O₃ at 1 873 K

纯氧化物表面张力主要与其内部离子间的键能有关，由于O^2-的半径比阳离子半径大，氧化物表面主要被O^2-所占据，表面张力的变化由表面O^2-与邻近阳离子的作用力决定。形成氧化物的离子的静电势(Z/r)大，氧化物中离子键分数越高，则氧化物的表面张力越大^[24]。纯组分氧化物静电势和离子键分数如图3所示^[9]。纯液态B₂O₃为表面活性物质，1 873 K时其表面张力约为0.104 N/m，仅为相同温度下MgO，FeO和SiO₂纯物质表面张力的1/6~1/3。Si⁴⁺和B³⁺虽然静电势很高，但其离子键分数较低(＜50%)，易形成共价键高、静电势小的络离子，从而其表面张力较小；Mg²⁺和Fe²⁺虽然静电势较小，但离子键分数较高，从而具有较高的表面张力。

3.3  含B₂O₃三元体系熔渣表面张力

1 873 K时含B₂O₃三元体系等温相图及液相线如图4所示。由于三元体系中存在的液-液相不互溶区的亚稳态区域，且含B₂O₃多元体系物相关系及热力学性质的缺乏，相关相图也需要进一步优化^[17]，因此，本文计算了1 873 K时含B₂O₃三元体系完全液相区内熔渣表面张力，计算结果如图4所示。结果表明，在MgO-B₂O₃-SiO₂体系1 873 K完全液相区范围内，熔渣表面张力在0.15~0.45 N/m范围内；由于熔渣中FeO将扩大熔渣液相区范围，因此B₂O₃-SiO₂-FeO体系1 873 K完全液相区范围比较大，熔渣表面张力在0.10~0.60 N/m范围内。在1 873 K完全液相区范围内，随着B₂O₃含量的增加，表面张力显著降低；随着SiO₂含量、MgO含量和FeO含量的增加，熔渣表面张力逐渐增大，但MgO含量和FeO含量对表面张力的影响更加显著。

3.4  MgO-B₂O₃-SiO₂-FeO体系中组分含量对熔渣表面张力的影响

采用本模型计算了1 873 K时MgO-B₂O₃-SiO₂- FeO体系表面张力，考察温度和组分含量对典型富硼渣表面张力的影响，计算结果如图5所示。图5(a)所示为渣中FeO质量分数为5%和B₂O₃质量分数为15%时，熔渣表面张力与MgO/SiO₂质量比(1.0~2.5)和温度(1 673~1 873 K)的关系。计算结果显示，熔渣表面张力随着MgO/SiO₂质量比的增加而逐渐增大，但变化的幅度逐渐降低；熔渣表面张力随着温度的增加而逐渐减小，且随着MgO/SiO₂质量比的增加，温度对表面张力的影响更加显著。

图3  1 873 K下纯氧化物的表面张力、离子键分数和阳离子静电势(Z/r)

Fig. 3  Surface tension, ion bond percentage and electrostatic potential of cations for pure oxide at 1 873 K

图4  1 873 K时含B₂O₃三元系等表面张力线的计算结果

Fig. 4  Calculated iso-surface tension lines of ternary system containing B₂O₃ at 1 873 K

图5(b)所示为1 873 K时渣中MgO/SiO₂质量比为1.5时，熔渣表面张力与FeO质量分数(1%~10%)和B₂O₃质量分数(分别为10%，15%，17%，18%，19%，20%和25%)的关系。结果显示，B₂O₃含量的增加将改变表面张力与FeO含量的变化关系。当B₂O₃质量分数＜17%时，熔渣表面张力随着FeO含量的增加而增大，当B₂O₃质量分数＞19%时，熔渣表面张力随着FeO含量的增加而降低，且FeO含量对表面张力的影响不如B₂O₃含量对表面张力的影响显著。1 873 K时纯组分FeO的表面张力大于MgO，B₂O₃和SiO₂纯物质表面张力，当B₂O₃含量较少时，熔渣表面张力随着FeO含量的增加而增加；当B₂O₃含量较大时，熔渣表面张力则主要受B₂O₃含量变化的影响，且MgO/SiO₂质量比和B₂O₃含量恒定情况下，随着熔渣中FeO含量的增加，B₂O₃质量分数相对增加，因此表面张力逐渐减少。

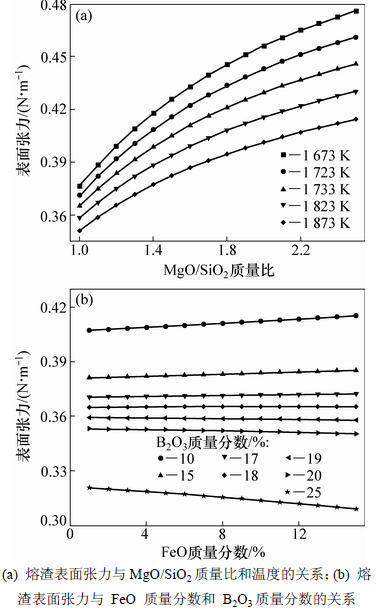
图5  MgO-B₂O₃-SiO₂-FeO体系熔渣表面张力与组分含量、温度的关系

Fig. 5  Relationship between surface tension of MgO-B₂O₃-SiO₂-FeO system with composition and temperature

4  结论

1) 基于熔渣结构的离子与分子共存理论和Butler方程建立了MgO-B₂O₃-SiO₂-FeO体系表面张力计算模型，相关体系模型计算结果与文献实验值吻合较好。

2) 含B₂O₃体系熔渣中，B₂O₃组元能够显著降低熔渣表面张力，纯氧化物表面张力与形成氧化物的阳离子静电势及氧化物中离子键分数有关。

3) MgO-B₂O₃-SiO₂-FeO体系表面张力随着B₂O₃含量增加和温度升高而显著降低，随着MgO/SiO₂比值的增加而逐渐增大。B₂O₃含量的增加将改变表面张力与FeO含量的变化关系，当B₂O₃质量分数＜17%时，熔渣表面张力随着FeO含量的增加而增大，当B₂O₃质量分数＞19%时，熔渣表面张力随着FeO含量的增加而降低。

参考文献：

[1] FU Xiaojiao, ZHAO Jiaqi, CHEN Shuangyin, et al. Comprehensive utilization of ludwigite ore based on metallizing reduction and magnetic separation[J]. J Iron Steel Res Int, 2015, 22: 672-680.

[2] SUI Zhitong, ZHANG Xianpeng, Yamauchi C. Precipitation selectivity of boron compounds from slags[J]. Acta Mater, 1999, 47: 1337-1344.

[3] MILLS K C, KEENE B J. Physical properties of BOS slags[J]. International Materials Reviews, 1987, 32(1/2): 1-120.

[4] Verein Deutscher Eisenhuttenleute. Slag atlas[M]. 2nd ed. Düsseldorf: Verlag Stahleisen GmbH, 1995: 50-88.

[5] 崔传孟，徐秀光，张显鹏，等. B₂O₃-MgO-SiO₂-Al₂O₃ -CaO系渣组成对熔体物性的影响[J]. 金属学报, 1996, 32(6): 637-641.

CUI Chuanmeng, XU Xiuguang, ZHANG Xianpeng, et al. Effect of composition of B₂O₃-MgO-SiO₂-Al₂O₃-CaO slag system on physical properties of melt[J]. Acta Metallurgica Sinica, 1996, 32(6): 637-641.

[6] YANG Lili, WANG Hongming, ZHU Xiang, et al. Effect of boron mud and CaF₂ on surface tension and density of CaO-SiO₂-B₂O₃ ternary slag systems[J]. J Iron Steel Res Int, 2014, 21(8): 745-748.

[7] KINGERY W D. Surface tension of some liquid oxides and their temperature coefficients[J]. J Am Ceram Soc, 1959, 42(1): 6-10.

[8] FUJINO S, HWANG C, MORINAGA K. Surface tension of PbO-B₂O₃ and Bi₂O₃-B₂O₃ glass melts[J]. Journal of Materials Science, 2005, 40(9/10): 2207-2212.

[9] HWANG C, RYUA B K, FUJINO S. Surface tension of bismuth borosilicate melts[J]. Thermochim Acta, 2012, 531: 70-74.

[10] 李建强，张晓瑞，陆平. 低膨胀硼硅酸盐玻璃熔体密度和表面张力测量[J]. 稀有金属材料与工程, 2009, 38(S2): 792-794.

LI Jianqiang, ZHANG Xiaorui, LU Ping. Surface tension and density of molten borosilicate glass measured by sessile drop method[J]. Rare Metal Materials and Engineering, 2009, 38(S2): 792-794.

[11] CHENG Guoguang, LIAO Nengbin. Calculation model for surface tension of slag melt[J]. J Iron Steel Res Int, 1999, 6(2): 17-20.

[12] 吴铖川, 成国光, 马琦琦. CaF₂-CaO-Al₂O₃-MgO-SiO₂渣系表面张力计算模型[J]. 上海金属, 2014, 36(3): 33-36.

WU Chenchuan, Cheng Guoguang, Ma Qiqi. Calculating model on the surface tension of CaF₂-CaO-Al₂O₃-MgO-SiO₂ slag system[J]. Shanghai Metals, 2014, 36(3): 33-36.

[13] CHENG Guoguang, LIAO Nengbin. Calculation model for surface tension of slag melt[J]. T Nonferr Metal Soc, 1998, 8(3): 5-10.

[14] TOROPOV N A, KONOVALOV P F. Binary system magnesium oxide-boric anhydride[J]. Zhurnal Fizicheskoi Khimii, 1940, 14(3): 1103-1109.

[15] MIYAGAWA S, HIRANO S, SOMIYA S. Phase relations in the system MgO-B₂O₃ and effects of boric oxide on grain growth of magnesia[J]. Journal of the Ceramic Association Japan, 1972, 80(2): 53-63.

[16] MUTLUER T, TIMUCIN M. Phase equilibria in the system MgO-B₂O₃[J]. J Am Ceram Soc, 1975, 58(5/6): 196-197.

[17] SUNKAR A S, MORITA K. Thermodynamic Properties of the MgO-BO_1.5, CaO-BO_1.5, SiO₂-BO_1.5, MgO-BO_1.5-SiO₂ and CaO-BO_1.5-SiO₂ slag systems at 1873K[J]. ISIJ Int, 2009, 49(11): 1649-1655.

[18] HUANG X M, ASANO K, FUJISAWA T, et al. Thermodynamic properties of the MgO-BO_1.5-SiO₂ system at 1723K[J]. ISIJ Int, 1996, 36(11): 1360-1365.

[19] ZHANG Jian. The application of the law of mass action in combination with the coexistence theory of slag structure to the multicomponent slag systems[J]. Acta Metallurgica Sinica (English Edition), 2001, 14(3): 177-190.

[20] NAPOLITANO A, MACEDO P B, HAWKINS E. Viscosity and density of boron trioxide[J]. J Am Ceram Soc, 1965, 48(12): 613-616.

[21] NAKAMOTO M, KIYOSE A, TANAKA T, et al. Evaluation of the surface tension of ternary silicate melts containing Al₂O₃, CaO, FeO, MgO or MnO[J]. ISIJ Int, 2007, 47(11): 38-43.

[22] 王广, 王静松, 薛庆国, 等. MgO-B₂O₃二元系熔渣质量作用浓度计算模型[J]. 中国有色金属学报, 2011, 21(12): 3144-3148.

WANG Guang, WANG Jinsong, XUE Qinguo, et al. Mass action concentration calculation model for MgO-B₂O₃ slag melt[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(12): 3144-3148.

[23] MILLS K C. The influence of structure on the physico-chemical properties of slags[J]. ISIJ Int, 1993, 33(11): 148-155.

[24] DUFFY J A, INGRAM M D. An interpretation of glass chemistry in terms of the optical basicity concept[J]. Journal of Non-Crystalline Solids, 1976, 21(3): 373-410.

(编辑  赵俊)

收稿日期：2016-06-14；修回日期：2016-09-04

基金项目(Foundation item)：江苏省自然科学基金资助项目(BK20130308; BK20140337)；国家自然科学基金资助项目(50874072; 51504155)；中国博士后科学基金资助项目(2014M561710)(Projects(BK20130308; BK20140337) supported by the Natural Science Foundation of Jiangsu Province; Projects(50874072; 51504155) supported by the National Natural Science Foundation of China; Project(2014M561710) supported by the China Postdoctoral Science Foundation)

通信作者：许继芳，博士，副教授，从事资源综合利用方面的研究；E-mail：xujifangsuda@163.com