基于粗糙集降维和相关向量机的长期用电需求预测方法
郭晓鹏1,杨淑霞1,杨里2
(1. 华北电力大学 经济与管理学院,北京,102206;
2. 福建省电力科学研究院,福建 福州,350007)
摘要:提出基于粗糙集降维的相关向量机用电量预测模型。选取1996—2010年北京市的GDP作为输入值,对应的全社会用电量作为输出值进行分析验证。研究结果表明:相关向量机是一种新的监督学习方法,与支持向量机相比,它更加稀疏,泛化能力更强且不需要设置惩罚因子,而粗糙集降维被用于从多个相关因素中筛选出适用于RVM回归模型的输入向量集,进而提高算法效率;基于相关向量机的用电量预测模型比经过优化参数后的支持向量机预测模型更优。
关键词:粗糙集;相关向量机;RVM回归模型;预测;用电需求
中图分类号:TU457;TU413.6 文献标志码:A 文章编号:1672-7207(2013)12-5133-06
Long-term electricity demand forecasting method based on rough set reduction and relevance vector machine
GUO Xiaopeng1, YANG Shuxia1, YANG Li2
(1. School of Economics and Management, North China Electric Power University, Beijing 102206, China;
2. Fujian Electric Power Research Institute, Fuzhou 350007, China)
Abstract: The electricity demand forecasting model based on the rough set and relevance vector machine was studied. To verify the validity of the model, the GDP and the electricity consumption data of Beijing from 1996 to 2010 were selected and analyzed with the GDP data was selected as input data, and the electricity consumption data used as output data. The results show that the relevance vector machine is a new supervising learning method. Compared with the support vector machine, it is sparser, with more generalization abilities and does not need to set the penalty factor. Rough set reduction is used to filter out the input vector for RVM regression model from a number of related factors, thus improving the efficiency of the algorithm. The electricity demand forecasting model based on the relevance vector machine is better than the support vector machine prediction model based on particle swarm optimization parameters.
Key words: rough set; relevance vector machine; RVM regression model; forecasting; electricity demand
用电量与城市、地区和国家的经济发展密切相关,作好用电量预测对电力规划、运行调度及电力市场交易等方面具有重要指导作用。近年来,与用电量需求和电力负荷等相关的预测方法多集中于智能算法方面,如将BP神经网络与马尔科夫链相结合预测中国电力需求[1],组合GM(1,1)和支持向量机(support vector machine,简称SVM)的电量预测模型[2]以及将粗糙集和SVM组合应用进行电力需求预测的模型[3]均具有较好的成果。在电力负荷预测方面,基于粒子群优化BP神经网络[4]以及经过混沌理论和粒子群优化的支持向量机[5-7]等预测模型效果良好。此外,通过引入遗传算法或粒子群优化算法来改进支持向量机参数选择的预测模型能够有效地改进传统支持向量机算法容易陷入局部极值、过学习等不足之处,取得了很好的效果[6-7]。近年来,相关向量机(relevance vector machine,简称RVM)[8]由于具有不需要对惩罚因子进行设置、更加稀疏和泛化能力更强等优点而受到关注,并在电力负荷预测[9]方面取得了较好的效果。在进行长期用电量预测时,需要充分考虑当地的GDP、居民用电和产业结构等多个因素。为了消除信息冗余,精简结构,取得较好的预测效果,本文作者构建基于粗糙集降维的相关向量机长期用电量预测模型,并结合具体的数据进行分析和探讨。
1 相关向量机回归预测模型
相关向量机常用于解决分类和回归等问题。其算法依据是在贝叶斯框架下进行回归估计获得预测值的分布,并得到基于核函数的稀疏解[10]。RVM的模型训练基于快速序列稀疏贝叶斯学习算法,训练速度比较快[11],能适用于多元回归和多类分类等问题。
利用RVM的稀疏贝叶斯回归模型来求解电量预测问题。假设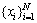 是训练集的输入值集合,
是训练集的输入值集合, 为输出值集合,则输入值和目标值之间的对应关系为
为输出值集合,则输入值和目标值之间的对应关系为
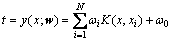 (1)
(1)
其中:w为权重向量;K(x,xi)为核函数;ω为对应的权重。与SVM不同的是,RVM还要从概率的角度出发考虑目标值的误差。在稀疏贝叶斯框架里,假定这个误差服从独立零均值的Gauss分布,即
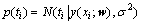 (2)
(2)
假设ti相互对立,则可得到训练集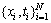 的似然估计为
的似然估计为
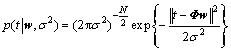 (3)
(3)
其中: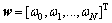 ;Φ为由各输入值代入核函数之后形成的矩阵,
;Φ为由各输入值代入核函数之后形成的矩阵,
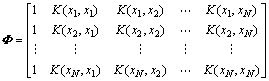
式(3)中的参数较多,容易陷入过拟合。为了解决这个问题,为权重向量w赋予零均值Gauss先验分布:
 (4)
(4)
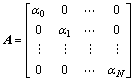
其中:α为N+1维的超参数(hyper parameters)向量。根据式(4)即可建立权重与超参数之间的一一对应关系来控制先验分布对超参数的影响,进而确保RVM的稀疏性。
根据前面的分布公式,结合贝叶斯原理,可得出参数的后验概率分布:

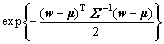 (5)
(5)
其中: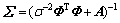 ;
;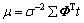 ;
; 。
。
式(5)中需要求得α和σ2的最可能(most-probable)解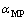 和
和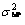 。从式(5)求取最可能解的过程比较复杂,最好采用数值计算中的迭代逼近算法来求取最佳的近似值,计算公式为:
。从式(5)求取最可能解的过程比较复杂,最好采用数值计算中的迭代逼近算法来求取最佳的近似值,计算公式为:
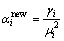 (6)
(6)
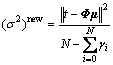 (7)
(7)
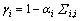 (8)
(8)
式中:μi为第i个后验平均权;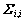 为
为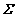 矩阵中第i项在对角线上的元素。若给定输入值x,则其对应的输出概率分布服从Gauss分布:
矩阵中第i项在对角线上的元素。若给定输入值x,则其对应的输出概率分布服从Gauss分布:
 (9)
(9)
预测值为
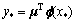 (10)
(10)
其中: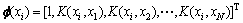 ,为Φ中的第i行向量。此时,求得的y*即为t*的预测值。
,为Φ中的第i行向量。此时,求得的y*即为t*的预测值。
相关向量机基于贝叶斯理论的回归预测过程见文献[8]。
2 粗糙集降维
粗集理论由Pawlak提出,是一种处理模糊和不确定知识的数学工具,用于分析和处理不精确、不一致或不完整的信息,并揭示潜在的规律。
通过粗糙集理论筛选用电量需求预测指标,其本质是约去多余的或意义不大的指标因素,同时保留对预测有重要影响的指标,即保留粗糙集的核集,这个过程实质上是求得预测指标集的最佳归约集[11-12]。
属性归约是指假设属性 是C的一个归约,当且仅当POSB(D)=POSc(D)时,B中的每个属性对于D都是不可缺少的。属性归约记为red(B,D),其步骤为:首先,求出属性归约集的核心;然后,运用归约算法计算归约集,并根据某种评判标准确定最佳归约集。
是C的一个归约,当且仅当POSB(D)=POSc(D)时,B中的每个属性对于D都是不可缺少的。属性归约记为red(B,D),其步骤为:首先,求出属性归约集的核心;然后,运用归约算法计算归约集,并根据某种评判标准确定最佳归约集。
根据条件属性C={c1,c2,…,cm}和决策属性D={d1,d2,…,dm}及对应的值V,来计算各条件属性对于决策属性的重要性。设条件属性为ci(i=1,2,…,m),决策属性为dj(j=1,2,…,n),则决策属性dj对于条件属性ci的相依度为
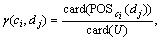 0≤γ(ci,dj)≤1 (11)
0≤γ(ci,dj)≤1 (11)
其中: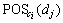 为条件属性ci对于决策属性dj的正区;card(·)为计算区域的基。设另有
为条件属性ci对于决策属性dj的正区;card(·)为计算区域的基。设另有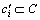 ,则
,则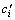 对于决策属性dj的重要度SGF为
对于决策属性dj的重要度SGF为
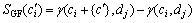 (12)
(12)
该算法首先计算每个条件属性即各影响因素对于决策属性的重要性,并根据每个条件属性的重要性排序,并按重要性从大到小将条件属性依次加入属性集redU,并考察属性集redU与决策属性之间的依赖程度,由此属性集redU将包含起重要作用的条件属性。然后,从属性集redU中按重要性从小到大均去掉属性。若去掉属性会造成依赖度变化,则恢复该属性,最后剩下的属性集就是最佳归约集。
3 粗糙集降维及相关向量机回归预测的流程
采用粗糙集降维和RVM进行预测的基本处理流程如下。
Step 1 初始化训练集。例如,对输入值和输出值进行标准化处理,以增大预测的精度。
Step 2 用粗糙集方法对处理后的数据集进行降维,选择恰当的相关向量。
Step 3 设置精度要求、迭代次数、超时时间等控制参数。
Step 4 根据训练集数据进行适应度学习,得到权重向量。训练过程要根据Step 2的控制参数来判断是否满足迭代中止条件。
Step 5 根据训练得到的模型,得到预测结果。
粗糙集降维及相关向量机预测流程如图1所示。
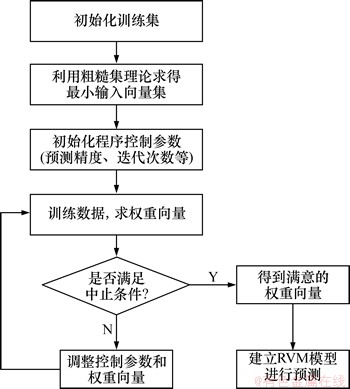
图1 粗糙集降维及相关向量机预测流程示意图
Fig. 1 Flow chart of RS-RVM forecasting model
4 实例分析
本文所涉及的预测过程全部采用Matlab编程实现。在程序的具体编码处理过程中,与RVM相关的预测算法主要借助了SPARSEBAYES Matlab Toolbox 2.0[13]。
另外,将基于粗糙集降维的RVM预测方法(简记为RVM)所得预测结果与SVM回归模型的预测结果进行对比,其中SVM的预测算法实现借助了LibSVM[14]工具包。利用SVM模型进行预测时,参数选择对最终的结果影响较大。为了避免根据经验指定参数可能导致的误差,用粒子群优化算法(particle swarm optimization,PSO)选择SVM参数,并在此基础上构建SVM预测模型,这使得本文中的预测方法与SVM预测方法之间的预测结果对比分析更有实际意义。
4.1 预测数据的选择与预处理
本文选取北京市1996—2010年全市用电量及北京市GDP、第一产业、第二产业、第三产业、城乡居民用电量比例等数据集进行分析。首先通过粗糙集对相关因子降维,最终选择采用GDP与全社会用电量进行分析验证。其中,GDP为RVM模型中的输入值,全社会用电量则作为输出值,这样,即可建立GDP与用电量之间的RVM回归预测模型。
本文从所有数据集中选取1996—2005年所对应的2组数据作为训练数据,据此进行适应度训练,从而建立RVM预测模型。模型建立后,再用2006—2010年的数据进行预测和验证。另外,为了获得算法更好收敛效果,将训练结果和预测结果进行[0,1]之间的归一化预处理。该预处理过程为
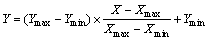
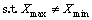 (13)
(13)
其中:X为原始数据集;Xmax为原始数据中的最大值;Xmin为原始数据中的最小值;Y为处理后的数据集;Ymax为处理后数据的最大值(取值为1);Ymin为处理后数据的最小值(取值为-1)。当Xmax =Xmin时,Y=X。
RVM模型训练数据之后,可得到如图2和表1所示的拟合结果。
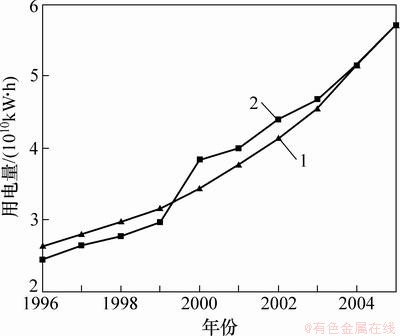
图2 RVM预测模型的拟合情况
Fig. 2 RVM forecasting model’s fitness chart
表1 RVM预测模型的拟合情况分析
Table 1 RVM forecasting model's fitness analysis
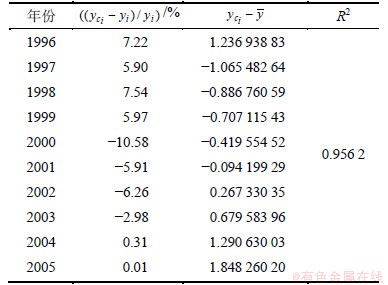
表1中: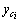 为第i个预测值;yi为第i个实际值;
为第i个预测值;yi为第i个实际值; 为实际数据的平均值。R2的计算公式为
为实际数据的平均值。R2的计算公式为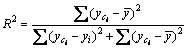 。由R2=0.956 2可知,本文预测模型的拟合效果很好。
。由R2=0.956 2可知,本文预测模型的拟合效果很好。
4.2 预测结果分析
预测完成后,要分析预测结果与实际结果之间的误差,同时,还要分析预测结果的均方根相对误差yRMSRE:
 (14)
(14)
其中: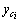 为第i个预测值;yi为对应的第i个实际值。
为第i个预测值;yi为对应的第i个实际值。
表2所示为真实用电量、RVM预测结果和基于PSO优化参数的SVM预测结果,并分别列出了各自的相对误差和均方根相对误差。其中,相对误差和均方根相对误差是预测效果的重要评价指标,其值越小,则模型的预测效果越好。
表2 北京市2006—2010年用电量及预测结果分析
Table 2 Electricity consumption data and predicted results of Beijing from 1996 to 2010 1010kW·h
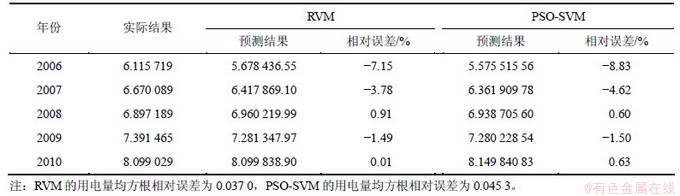
原始结果、RVM预测结果和PSO-SVM预测结果的对比如图3所示;RVM预测误差和PSO-SVM预测误差之间的对比如图4所示。
根据经验,相对误差的绝对值小于3%的预测结果是比较理想的。由表2可知:基于RVM和PSO-SVM预测模型所产生的5个相对误差中,后3年的都小于3%;在2个预测模型中,出现最大误差的点均为2006年的用电量,其相对误差分别为-7.15%和-8.83%;2007年的预测误差接近3%。这表明RVM预测模型和PSO-SVM模型的预测效果都比较好。就本文的预测结果而言,RVM预测模型在预测精度上略比PSO-SVM预测模型的高(RVM预测的5个预测数据中只有1个误差比PSO-SVM预测模型的高,但该相对误差也仅为0.91%)。

图3 原始数据、RVM预测结果和PSO-SVM预测结果对照图
Fig. 3 Comparison among original results,RVM predicted results and PSO-SVM predicted results

图4 RVM预测结果和PSO-SVM预测结果的误差对比图
Fig. 4 Comparison ofa predicted results’ relative errors between RVM and PSO-SVM
从均方根相对误差(表2)看,RVM为0.037 0,而PSO-SVM为0.045 3,预测结果都比较理想。按照本文的试验结果,RVM的预测效果比 PSO-SVM的好。
另外,未经优化的SVM算法在参数选择上受经验影响较大,会直接影响预测精度。若参数选择不当,则预测误差会很大。为了取得最好的SVM预测结果,本文采用粒子群优化算法来获取SVM预测模型的最佳参数。从算法实现的难易程度而言,RVM未与其他启发式算法或智能算法相结合,编程实现较简单。
5 结论
(1) RVM回归预测模型基于贝叶斯原理,与SVM相比更为稀疏,其训练时间更短。另外,RVM进行回归预测时,无需对惩罚因子进行设置,能有效避免过学习等问题。RVM的参数设置比SVM更加简单,其算法的编程实现更加简洁、直观。
(2) 通过粗糙集降维可筛选出输入相关向量最佳规约集,从而在提高RVM长期用电量预测模型效率的同时,能够确保其预测精度。
(3) 本文采用的RVM预测模型在预测用电量方面具有良好的效果,其预测精度也略比经过PSO寻参优化后的SVM模型高,证明了RVM模型的有效性。
(4) 本文没有涉及RVM模型与其他智能算法相结合等方面的优化等问题。事实上,RVM在处理小样本数据之时效果较好,但涉及大量的训练数据时处理性能较差,这些问题有待进一步研究。
参考文献:
[1] LI Cunbin, WANG Kecheng. A new grey forecasting model based on BP neural network and Markov chain[J]. Journal of Central South University of Technology, 2007, 14(5): 713-718.
[2] 宋晓华, 祖丕娥, 伊静, 等. 基于改进GM(1,1)和SVM的长期电量优化组合预测模型[J]. 中南大学学报: 自然科学版, 2012, 43(5): 1803-1807.
SONG Xiaohua, ZU Pie, YI Jing, et al. An optimally combined forecast model for long-term power demand based on improved grey and SVM model[J]. Journal of Central South University: Science and Technology, 2012, 43(5): 1803-1807.
[3] YANG Shuxia, CAO Yuan, LIU Da, et al. RS-SVM forecasting model and power supply-demand forecast[J]. Journal of Central South University of Technology, 2011, 18(6): 2074-2079.
[4] 崔吉峰, 乞建勋, 杨尚东. 基于粒子群改进BP 神经网络的组合预测模型及其应用[J]. 中南大学学报: 自然科学版, 2009, 40(1): 190-194.
CUI Jifeng, QI Jianxun, YANG Shangdong. Combined forecasting model based on BP improved by PSO and its application[J]. Journal of Central South University: Science and Technology, 2009, 40(1): 190-194.
[5] NIU Dongxiao, WANG Yongli, MA Xiaoyong. Optimization of support vector machine power load forecasting model based on data mining and Lyapunov exponents[J]. Journal of Central South University of Technology, 2010, 17(2): 406-412.
[6] HE Yongxiu, HE Haiying, WANG Yuejin, et al. Forecasting model of residential load based on general regression neural network and PSO-Bayes least squares support vector machine[J]. Journal of Central South University of Technology, 2011, 18(4): 1184-1192.
[7] LI Yanbin, ZHANG Ning, LI Cunbin. Support vector machine forecasting method improved by chaotic particle swarm optimization and its application[J]. Journal of Central South University of Technology, 2009, 16(3): 478-481.
[8] Tipping M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001, 13(1): 211-244.
[9] 黄帅栋, 卫志农, 高宗和, 等. 基于非负矩阵分解的相关向量机短期负荷预测模型[J]. 电力系统自动化, 2012, 36(11): 62-66.
HUANG Shuaidong, WEI Zhinong, GAO Zonghe, et al. A short-term load forecasting model based on relevance vector machine with nonnegative matrix factorization[J]. Automation of Electric Power Systems, 2012, 36(11): 62-66.
[10] 杨国鹏, 周欣, 余旭初. 稀疏贝叶斯模型与相关向量机学习研究[J]. 计算机科学, 2010, 37(7): 225-228.
YANG Guopeng, ZHOU Xin, YU Xuchu. Research on sparse bayesian model and the relevance vector machine[J]. Computer Science, 2010, 37(7): 225-228.
[11] XIE Gang, ZHANG Jinlong, Lai K K, et al. Variable precision rough set for group decision-making: An application[J]. International Journal of Approximate Reasoning, 2008, 49(2): 331-343.
[12] QIAN Yuhua, LIANG Jiye, Pedrycz W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174(9/10): 597-618.
[13] Tipping M E. Sparse Bayesian Models (& the RVM)[EB/OL]. [2013-11-14]. http://www.miketipping.com/sparsebayes.htm.
[14] Chang C C, Lin C J. LIBSVM: A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 1-27.
(编辑 陈灿华)
收稿日期:2012-12-03;修回日期:2013-03-02
基金项目:国家自然科学基金资助项目(71071054);中央高校基本科研业务费专项资金资助项目(11QR34)
通信作者:郭晓鹏(1979-),男,河南济源人,博士,讲师,从事电力经济等方面的研究;电话:13520328997;E-mail:guoxp2004@gmail.com