J. Cent. South Univ. Technol. (2009) 16: 0851-0856
DOI: 10.1007/s11771-009-0141-0

Numerical analysis on Joule heating of double-loop channel induction furnaces
ZHAO Tao(赵 涛)1, ZHOU Jie-min(周孑民)1, XIONG Jia-zheng(熊家政)2, LI Yong(李 勇)2
(1. School of Energy Science and Power Engineering, Central South University, Changsha 410083, China;
2. Zhuzhou Torch Industrial Furnace Limited Company, Zhuzhou 412005, China)
Abstract: In order to investigate Joule heating power, a three-dimensional finite element model (FEM) was developed to predict Joule heating power in the channels of double-loop inductor. The simulated results were compared with experimental data from low load trials for a 400 kW inductor. The results, such as power factor and Joule heating power, show reasonable correlation with experimental data, and Joule heating rate reaches the maximum at the corners and the minimum at the centre of the cross-section area. With increasing relative permeability of iron core, length of coils, current frequency and resistivity of metal melt, the power factor and Joule heating power change. It is concluded that current frequency, the resistivity and length of the coil play a critical role in determining the power factor and Joule heating power, whereas relative permeability of the magnetic core shows no significant influence on them.
Key words: numerical simulation; channel induction furnace; Joule heating; power factor
1 Introduction
Twin-channel induction furnaces are extensively used for melting and holding metals and alloys in many processing industries. This is due to their high overall efficiency, good degassing and homogenization of the melt, low oxide and slag formation and low energy cost [1-2]. It is generally accepted that the function of the inductor is to induce high current densities in the channels and heat the metal through Joule heating [3-4]. The principle of a double channel induction furnace is based on the effect of electromagnetic induction, and significant axial flows along the channels axes are detected [5-7].
The Joule heating in the channel has been investigated mainly by simplified analytical models and full-scale finite element analysis (FEA). Unfortunately, the application of analytical models is limited because they are complex and costly. For further studies, the most commonly used tool is the finite element method. RAPPAZ and SWIERKOSZ [8] conducted mathematical modeling and simulation of induction heating processes. BODART et al [9] performed numerical investigation of optimal control of induction heating process.
It is evident that the coupled physical phenomena involved in the function of the channel induction furnaces are not fully understood and experimental investigations using cold mercury or Wood’s metal are inadequate and unrealistic. In the present work, an attempt was made to predict Joule heating rate of double-loop channel and the power factor in a 400 kW inductor using the finite element analysis software.
2 3D model
2.1 Analysis software
The channel induction furnace is a good example of multi-field coupling engineering system, which explains its complexity and difficulty in predicting the behavior of the molten metal under normal and abnormal operating conditions. In induction furnaces, electricity, electromagnetism, gravitational phenomena, fluid flow and heat transferring continuously interact in a non-linear fashion [7-9]. Computer modeling of such a system will ideally require direct coupling of all these phenomena, preferably in a single software package. However, this is still impractical for the following reasons: there is no software package which is capable of coupling all the above-mentioned physical phenomena simultaneously; because modeling of all coupled phenomena is inefficient, computing time can be very long and software cost may be very high [10-11]; modelers of high level of skill in different fields are required.
For engineering purpose it might be adequate to model using an electromagnetic package with carefully selected boundary conditions [12-13]. In current work the finite element analysis software is used, which can investigate in electromagnetic field and predict Joule heating rate in the double-channel of an inductor. The software is ANSYS 8.0, which possesses graphical modeler and can be used as 3D interactive pre- and post-processor. The process to predict Joule heating and power factor is shown in Fig.1.
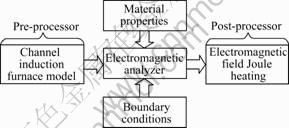
Fig.1 Analysis scheme of Joule heating rate
2.2 Meshing and boundary condition
Fig.2 shows the 3D model of 400 kW inductor generated by the graphical modeler. The model is used to predict the electromagnetic regime and Joule heating rate of the molten metal in the channel of double-loop channel inductor. Because of the strong magnetic coupling in the system, the magnetic boundary condition on the outer surface of refractory is imposed
n×A=0 (1)
where n is the unit normal vector to the boundary, and A is the magnetic vector potential.

Fig.2 Diagram of 400 kW inductor model without refractory
2.3 Input data
The input data required for the solution included the material properties, such as relative permeability and resistivity, when the load was given as current density. Material properties were obtained from published data and were assumed to be constant, temperature dependent or temperature difference dependent [14]. In this work, the properties were assumed to be constant. The molten metal was taken as molten zinc and the refractory as alumina. The only physical field involved in this solution was the electromagnetic field and the load was expressed as current density.
 (2)
(2)
where Js is the current density on the cross-section area of the coils, I is the current passing through the primary coils, and A1 is the cross-section area of the coils.
3 Results and discussion
3.1 Geometrical convergence
First, the geometrical convergence of the 3D model was tested. For this purpose, the model was recalculated for several different discretizations that differed mainly in meshing of the channel area. Variations of the total heating power and total current through the channel were observed. The dependence of the heating power and current through the channel on the maximum edge size of elements in the subdomains representing the channel is displayed in Table 1.
Table 1 Dependence of meshing of channel on heating and current through inductor
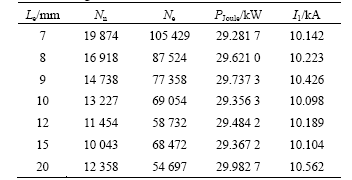
In Table 1, Le is the maximum element edge size in the area of the channel, Nn is the number of nodes, Ne is the number of elements, PJoule is the Joule heating power, and I1 is the inducted current passing through the channels. It can be concluded that the fluctuations of the Joule heating power and current in the inductor are small and can be neglected.
In order to verify the reliability of 3D model, simulation results of magnetic flux density (B) in the cross section area of the central channel below 0.3 m of the inlet were compared with the measurements by small coil method [15], as shown in Fig.3.
The simulated and measured results of low load trial for 400 kW inductor are shown in Table 2. In Table 2, P is the power of the coils, I2 is the current of the coils,  is the measurement of power factor, and
is the measurement of power factor, and is the predicted result of power factor. It can be seen that although there is inaccuracy, the simulated results agree reasonably with the measured results when the boundary
is the predicted result of power factor. It can be seen that although there is inaccuracy, the simulated results agree reasonably with the measured results when the boundary
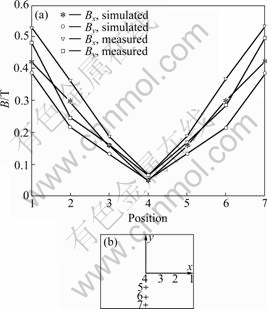
Fig.3 Comparison of magnetic flux density (a) at different positions of cross section area (b) by measurement and simulation at input voltage of 150 V and frequency of 50 Hz
Table 2 Simulated and measured results for 400 kW inductor
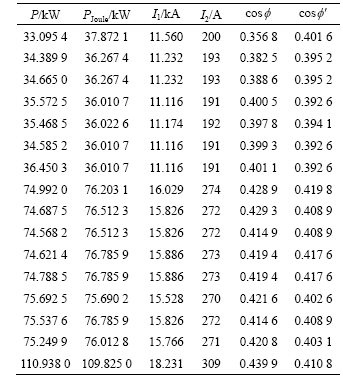
conditions and parameters are set correctly.
3.2 Electromagnetic distribution
The model was then applied to test the electromagnetic distribution in the channel. The problem was solved on a mesh consisting of 362 450 nodes, and 190 538 elements and the maximum edge in the channel area was set as 7 mm. The input current of coils was 190 A and the current frequency was 50 Hz.
Fig.4 shows the electromagnetic contours of magnetic field strength in the channel. The Joule heating power is 32.163 7 kW and the current passing through the channel is 11.032 kA. Fig.5 shows the inducted current densities, the magnetic field strength and Joule heating rate contours of molten zinc in the cross-section area of the channel. The cross-section area is located below the inlet of central channel 0.30 m. The inducted current densities, magnetic field strength and Joule heating rate reach the maximum at the interface and the minimum at the centre of the cross-section area. The magnetic field acts primarily in the planes perpendicular to the axes of the channels and the magnetic field strength (H) in the cross-sectional area exhibits vortex pattern resulted from the interaction of the stray primary magnetic field and the magnetic field of the inducted current in the melt loops [16].
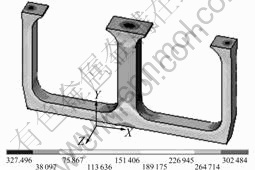
Fig.4 Magnetic field strength contours in channel (Unit: A/m)
3.3 Relative permeability
The model with rectangular cross-section of the channel was used to compute relative permeability (μr) of the magnetic core increasing from 5 000 to 10 000. The input current of coils was 190 A and the current frequency was 50 Hz. Table 3 shows the simulated results. The eddy loss of iron core is not considered.
A slight increase of the power factor, the inducted current and Joule heating power are observed. They are small in contrast with the improvement of relative permeability. For example, Joule heating power is respectively 32.163 7 and 32.321 8 kW, the inducted current is respectively 11.032 and 11.139 kA in two cases: low (5 000) and high (10 000) relative permeability.
These results indicate that the relative permeability is not the main factor influencing Joule heating power of channel in this work. The magnetic field is canalized by the high permeable laminated core, the leakage flux and, in turn, the corresponding losses of electrical energy caused by the Joule effect in the surrounding conductors are attenuated. For the eddy loss of iron core cannot be estimated by the codes used in this work, further research

Fig.5 Inducted current density (a), magnetic flux density (b) and Joule heating rate (c) contours of pure zinc in cross-section area of channel
is required to analyze the influence of relative permeability of the magnetic core on inductors.
3.4 Height of coils
The same value of relative permeability (μr=5 000) was used to investigate the influence of height of coils (L) on Joule heating rate and power factor. Table 4 shows the results when L changes from 451.5 to 551.5 mm. The input current of coils is taken as 667.5 A and the current frequency as 50 Hz.
Table 3 Results when relative permeability changes from 5 000 to 10 000
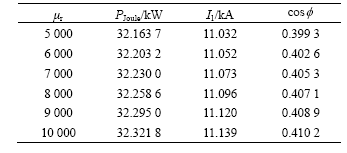
Table 4 Results while length of coils changes from 451.5 to 551.5 mm
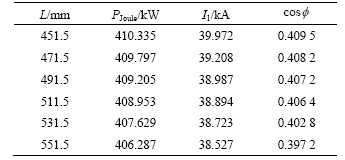
Joule heating power and power factor decrease with increasing L. For example, Joule heating power is respectively 410.335 and 406.287 kW, the power factor is respectively 0.409 5 and 0.397 2 in two cases: short (451.5 mm) and long (551.5 mm).
These results indicate that the height of coils play a role in determining Joule heating power and power factor. Because changes in height or thickness of the primary coil affect the coil resistance and inductance, the power factor and electricity efficiency also change. Tight coils can canalize the magnetic coupling in the system and reduce the leakage flux.
3.5 Current frequency
The model was used to compute current frequency (f) varying from 50 to 500 Hz to investigate the influence of frequency on Joule heating rate and power factor. The input current of coils is 190 A. Table 5 shows the simulated results when current frequency varies from 50 to 500 Hz.
Table 5 shows that Joule heating power is improved obviously with increasing current frequency. When frequency increases from 50 to 500 Hz, the Joule heating power rises from 32.164 to 68.734 kW and the increase rate is 114.0%. The power factor decreases quickly with the increasing current frequency. For example, the power factor is respectively 0.398 6 and 0.037 8 in two cases:
Table 5 Results when current frequency (f) varies between 50 and 500 Hz
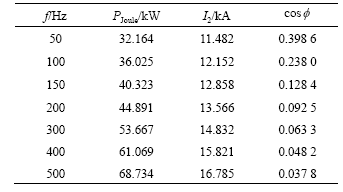
low (50 Hz) and high (500 Hz).
These results indicate that current frequency plays a critical role in determining the Joule heating rate and power factor due to electromagnetic induction. Because the increase in current frequency enhances the energy and energy convey of electromagnetic field, it requires more energy reserves to convey electromagnetic waves in space. As a result, the impendence and reactive power in the system increase, and the power factor decreases. With increasing current frequency, the output power density increases obviously and the power factor decreases because of increasing resistance in the system influenced by the current frequency. Further research is required to choose the suitable frequency for a particular design if efficiency and energy conversion issues of inductors are to be addressed.
3.6 Resistivity of molten metal
The model was used to compute the resistivity (ρ) of molten metal varying between 0.01×10-6 and 1.36×10-6 Ω?cm. The voltage imposed on coils is 750 V. The simulated results are shown in Table 6, where R is the resistance, and Z is the impedance.
Table 6 shows that Joule heating power and power factor improve obviously with the increase of the resistivity of metal melt in the channel while the current in the coils and the power imposed on the coils decrease obviously. When the resistivity of molten metal increases between 0.01×10-6 and 1.36×10-6 Ω?cm, Joule heating power rises from 52.146 to 710.916 kW and the power factor changes from 0.052 to 0.981, respectively. In Fig.6, the power imposed on the coils decreases and the Joule heating power increases obviously with the increase of resistivity. The Joule heating power is step by step closer to the power imposed on the coils as a result of the increase of power factor.
These results indicate that the resistivity of metal melt in the channel plays a critical role in determining Joule heating power and power factor. As one of the important parameters, resistivity of molten metal influences impedance in the system. Because the increase in resistivity enhances reflected impedance on the primary coils and coupling between the coils and the loops of molten metal, when voltage is constant, less electromagnetic requirement for energy convey is needed and less electric energy oscillates in electric circuit compared with those at low resistivity. Further research is required to analyze the influence of the resistivity on Joule heating power for a particular design if economy issues of inductors are to be addresse
Table 6 Results when resistivity of molten metal varies between 0.01×10-6 and 1.36×10-6 Ω?cm
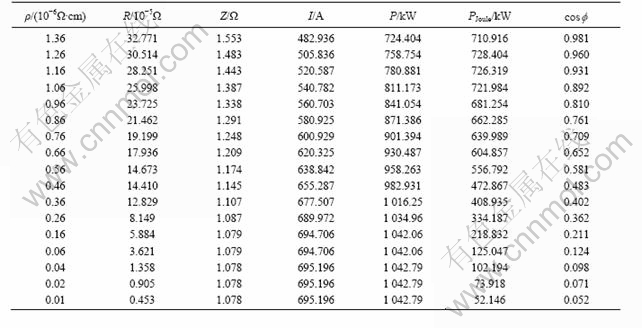
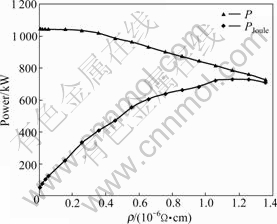
Fig.6 Simulated relationships among ρ, P and PJoule
4 Conclusions
(1) Because good electromagnetic coupling of the magnetic core in channel induction furnace, increasing relative permeability of the magnetic core is not an efficient approach to enhance Joule heating power and power factor in the system, when relative permeability of the magnetic core is greater than a certain value, for example, 5 000 in this work.
(2) The length of coils plays a role in determining Joule heating power. Tight coils are beneficial to the performance of the inductor. It is required to quantify the optimum length of coils for a particular design if performance issues of inductors are to be addressed.
(3) Joule heating power increases and the power factor decreases obviously with increasing current frequency. High current frequency is beneficial to Joule heating power, however, it also aggravates the impendence in the system. The suitable current frequency is an important element influencing the performance of the double-loop channel inductor.
(4) Both Joule heating power and the power factor increase obviously with the increase of resistivity of molten metal in the channel, the input power on coils decreases as the result of the increase of impedance. The Joule heating power is step by step close to the power imposed on the coils as a result of the increase in power factor. The resistivity of molten metal is an important operating parameter to the performance of inductor.
(5) During the development of the model, only when the boundary conditions and parameters are set correctly, the simulated results show reasonable agreement with the measured results. FEA is an effective approach to study the induction heating.
(6) In this work, only the electromagnetic field is considered, while the flow rate out of the side channels contributing to mass transport between the inductor and the pot and the vortex flow in the cross-sectional areas of the channels are neglected. Further work, both experimental and analytical, is required to quantify the flow speed in channel inductors and correlate that with input energy and temperature regime in the inductor.
References
[1] ZHANG Shu-fang. Induction heating manual [M]. Beijing: Defense Industry Press, 1985. (in Chinese)
[2] JIN Xiao-chang. Surface effects in induction heating [J]. Journal of Wuhan Institute of Chemical Technology, 1995, 17(4): 65-68.
[3] DAVIES E J. Conduction and induction heating [M]. London: Peregrinus, 1990.
[4] HAN Zhi-cheng. Electromagnetic metallurgy [M]. Beijing: Metallurgical Industry Press, 2001. (in Chinese)
[5] MOROS A, HUNT J C R. Recirculating flows in the cross-section of a channel induction furnace [J]. Heat Mass Transfer, 1988, 31(7): 1497-1515.
[6] VIVES C, RICOU R. Magnetohydrodynamic flows in a channel induction furnace [J]. Metal Trans, 1991, 22B: 193-209.
[7] DREWAK R, MUHLBAUER A. Controlling heat transfer in a channel-induction furnace [C]// Proceedings of Advances in Engineering Heat Transfer. Riga, Latvia, 1995.
[8] RAPPAZ J, SWIERKOSZ M. Mathematical modeling and simulation of induction heating processes [J]. Appl Math Comp Sci, 1996, 6(2): 207-221.
[9] BODART O, BOUREAU A V, TOUZANI R. Numerical investigation of optimal control of induction heating process [J]. Appl Math Modeling, 2001, 25: 697-712.
[10] DREWAK R, JAKOVICH A, MUHLBAUER A A, NACKE B. Experimental and numerical investigations of the melt flow in channel-induction furnaces [J]. Magnitnaya Gidrodinamica, 1996, 32(4): 433-443.
[11] ZHAO C, FAUTRELLE Y. Turbulent fluid flow in induction furnaces [C]// SZEKELY J. Magnetohydrodynamics in Process Metallurgy. Warrendule: The Minerals, Metals and Materials Society, 1991.
[12] SUN Jun-sheng, WU Chuan-song. The electromagnetic force and its influence on the weldpool fluid flow in MIG welding [J]. Acta Phys Sin, 2001, 50: 209-216. (in Chinese)
[13] ZI Bing-tao, YAO Ke-fu. Numerical simulation of liquid alloy flow field during solidification under applied pulsed magnetic field [J]. Acta Phys Sin, 2003, 52: 115-119. (in Chinese)
[14] WANG Hong-ming, CHEN Guo-xing, REN Zhong-ming, LEI Zuo-sheng, LI Gui-rong, XIA Xiao-jiang, DAI Qi-xun. Magnetic induction density of high frequency magnetic field for electromagnetic continuous casting [J]. Foundry Technology, 2006, 27(7): 737-739.
[15] CHENG Chang-le, CHEN Zhao. Influence of rotating magnetic field on the formation of solidification microstructure [J]. Acta Phys Sin, 2008, 57: 6277-6282. (in Chinese)
[16] LU Wei-de. Discussion of design of channel induction furnace for heavy non-ferrous metals [M]. Beijing: Non-ferrous Metal Press, 1992. (in Chinese)
(Edited by YANG You-ping)
Foundation item: Project(50876116) supported by the National Natural Science Foundation of China; Project(2007CK3077) supported by Innovative Program of Hunan Science and Technology Agency; Project(1343-77225) supported by the Graduate School of Central South University
Received date: 2008-11-20; Accepted date: 2009-03-17
Corresponding author: ZHAO Tao, Doctoral candidate; Tel: +86-13054178261; E-mail: csuzhaotao@yahoo.com.cn