DOI: 10.11817/j.issn.1672-7207.2017.09.014

基于层合叠加理论的CFRP多向层合板铣削力建模

王福吉，朱浩杰，宿友亮，高汉卿，毕广健

(大连理工大学 机械工程学院，辽宁 大连，116023)

摘要：针对碳纤维增强树脂基复合材料(CFRP)多向层合板设计中常用的典型纤维铺层方向，实验研究CFRP单向层合板的铣削力随纤维方向角及加工参数的变化规律，使用BP神经网络，获取不同加工参数下的CFRP 4种典型铺层方向单向层合板铣削力数据；基于BP神经网络结果数据和切削力层合叠加理论，建立CFRP多向层合板铣削力预测模型。研究结果表明：纤维方向角是影响铣削力的最主要的因素，该CFRP多向层合板铣削力预测模型精度可以达到85%以上。

关键词：CFRP多向层合板；切边精加工；铣削力预测；BP神经网络；层合叠加理论

中图分类号：TB332；TG156        文献标志码：A         文章编号：1672-7207(2017)09-2352-11

Modeling about milling force for multidirectional CFRP based on theory of superposition

WANG Fuji, ZHU Haojie, SU Youliang, GAO Hanqing, BI Guangjian

(College of Mechanical Engineering, Dalian University of Technology, Dalian 116023, China)

Abstract: Experiments were conducted to investigate the relationship between cutting parameters and cutting force of representative unidirectional CFRP. By using the back-propagation artificial neural network, the milling forces of the representative unidirectional CFRP were obtained. Based on the time-domain graph of unidirectional CFRP milling forces’ and the theory of superposition, a prediction model of multidirectional CFRP cutting forces was established and modified, and the verification experiments were conducted. The results show that the cutting angel is the most important factor to influence the milling forces. The prediction accuracy is above 85%.

Key words: multidirectional CFRP; edge trimming; milling force prediction; BP neural network; theory of superposition

碳纤维增强树脂基复合材料(CFRP)由于其高强低质的特征以及耐疲劳、抗腐蚀等优良特性，近年来在航空航天行业中得到了越来越广泛的应用。铣削作为CFRP构件的重要加工方式，在诸如切边、开窗等方面得到了普遍应用。铣削加工中，若工艺参数选用不合理将导致较大的铣削力，进而引起分层、撕裂、毛刺、烧伤等现象，严重降低零件的力学性能甚至导致零件报废^[1]；同时，过大的铣削力将加速刀具的磨损，造成刀具浪费，而且刀具磨损后将进一步加剧损伤^[2]，所以工艺技术人员往往通过比较保守的切削用量和多次精加工的方法来保证表面质量和加工精度，操作过程复杂，效率低下。因此，对CFRP多向层合板构件的铣削力进行建模预测，在合适的范围内优选加工参数，对于保证加工质量，提高加工效率，具有非常重要的意义。由于CFRP各向异性特点，较难对CFRP多向层合板铣削力进行理论建模分析。康永峰等^[3-5]进行CFRP多向层合板铣削实验，通过线性回归等方式建立经验公式，结果发现：切深是铣削力变化的主要影响因素，铣削力随切深和进给的增加而逐渐增大，随转速的提高而逐渐降低；SLAMANI等^[6]研究了切削速度与进给速度的比值对铣削力的影响规律，建立了考虑刀具磨损的铣削力预测经验公式，结果表明，铣削合力随着切削速度与进给速度比值的增大而减小，随切削速度与进给速度比值的减小而增大。上述研究均未考虑铺层方向对铣削力的影响，仅可预测特定的CFRP多向层合板加工中的铣削力。KARPAT等^[7-9]建立了CFRP单向层合板铣削力预测机械模型，并提出使用正弦函数能够较好地表征铣削力和切削角度之间的关系，还考虑铺层方向对多向层合板铣削力进行了预测。韩胜超等^[10]以不同进给速度分别对４种典型纤维方向的单向层合板进行侧铣加工，通过测得的铣削力数据计算各自的铣削力系数，根据力学矢量叠加原理得到了CFRP多向层合板铣削力系数的简化计算表达式。KALLA等^[11-13]通过铣削实验结合人工神经网络获得单向板的铣削力系数K_c和K_t的预测模型，提出对于各向异性、多铺层结构、多加工参数的CFRP多向层合板的铣削力预测，神经网络的方法比线性回归的方法具有更高的精度。大型航空复合材料制件多向层合板的铺层设计中多采用纤维方向角为0°，45°，90°和135°的4种典型的铺层方向，但其铺层结构、铺层顺序和铺层厚度多种多样，因此建立考虑铺层方向的具有普适性的CFRP多向层合板铣削力模型具有重要意义。对航空用CFRP多向层合板进行铣削精加工的实质是同时对4种典型铺层方向的CFRP单向板进行铣削加工，WANG等^[14]对CFRP多向层合板进行直角切削实验时发现：CFRP多向层合板的切削力等效于组成它的各CFRP单向板切削力之和。鉴于此，本文作者提出通过叠加CFRP单向板铣削力来计算CFRP多向层合板铣削力的方法：通过BP神经网络获取了CFRP单向板的铣削力预测数据，在预测数据的基础上建立了从CFRP单向板到CFRP多向层合板的铣削力预测模型，并根据不同纤维方向角下的铣削力时域信号曲线特征加以修正，最终实现了对任意CFRP多向层合板铣削力准确预测。

1  切边精加工过程分析

大型飞机主承力结构中的CFRP制件多是由4种典型铺层方向的单向板层叠而成，如图1所示，由于CFRP材料纤维增强的特征，其切削过程呈现明显的各向异性，为更准确地分析切削过程，定义纤维方向角(用ψ表示)为：刀具进给方向逆时针旋转到与纤维方向重合所转过的角度，如图2所示，其中f_v为刀具进给速度方向。

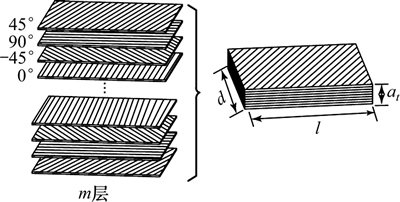
图1  CFRP多向层合板叠层示意图

Fig. 1  Schematic of multidirectional CFRP

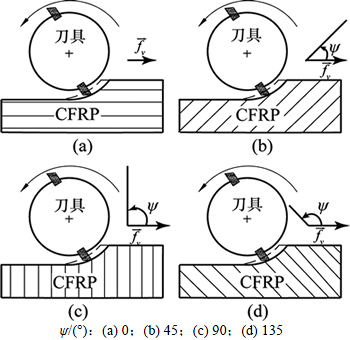
图2  4种典型的纤维方向角

Fig. 2  Schematic of representative fiber orientation angles

铣削CFRP多向层合板制件的本质为同时铣削多个CFRP单向板，工程实际中常使用双直刃PCD铣刀对CFRP多向层合板制件进行铣削精加工，如图3所示，刀具每齿进给量与刀具半径相比极小，刀齿摆线轨迹可等效为圆形轨迹；φ是刀齿旋转角，刀齿从A点切入材料，此时的刀齿旋转角为切入角，记作φ_st，刀齿从B点切出材料，此时的刀齿旋转角为切出角，记作φ_ex。由几何关系可得，

             (1)

其中：R为刀具半径；a_e为径向切深。

铣削过程中的单齿切削时间为

               (2)

其中：T为刀具旋转周期，

                  (3)

其中：N为主轴转速，r/min。

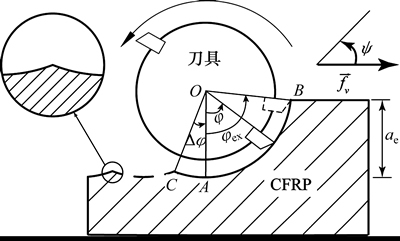
图3  铣削过程示意图

Fig. 3  Schematic diagram of milling process

2  实验设计

使用T800/3900B单向预浸料经热压固化制成实验样件，在185 ℃和0.62 MPa下固化3 h后随炉冷却，其纤维体积分数按照ASTM D2584标准灼烧，测得纤维体积分数可达65%，纤维密度较高。单层预浸料厚度为0.2 mm，CFRP单向层合板共15层，厚度为3 mm，纤维方向角为0°，45°，90°和135°；CFRP多向层合板样件总共20层，总厚度为4 mm，铺层方向为[-45, 0, 45, 90]_2S, 0, 0, 0, 0, [-45, 0, 45, 90]_2S；使用金刚石锯片将固化好的CFRP的裁成长×宽为50 mm×50 mm样品。实验使用PCD双直刃铣刀，刀具直径为10 mm，前角为3°，后角为5°，刀尖圆弧半径为7 μm，刀具如图4所示。采用MIKRON H500速铣床进行铣削加工，切削过程中的铣削力通过KISTLER 9253B三分量测力仪实时采集，实验布置如图5所示。

图4  双直刃铣刀

Fig. 4  Milling tool

图5  实验布置图

Fig. 5  Experimental setup

为减小CFRP样件边缘的表层分层损失，采用逆铣方式对CFRP样件进行切边精加工，切削参数参照工程经验及切削机理研究^[15]选取，实验参数如表1所示，所取力均为最大值，为切削信号稳定段中5个连续周期最大值的算术平均值。

表1  铣削实验参数

Table 1  Experimental parameters for milling process

3  单向板铣削力

3.1  铣削力测量及时域特征

对CFRP单向层合板的铣削力进行测量，三向铣削力信号呈现间歇性变化，其中实验参数为ψ=45°，N=1 910 r/min，f_z=0.18 mm的原始切削力信号如所图6所示，其中，f_z为每齿进给量。从图6可以看出：切削力信号的末端出现了振动，这是由于切削过程中刀具高速旋转所引起的，使用低通滤波器对原始信号进行滤波，滤波后的信号如图7所示。

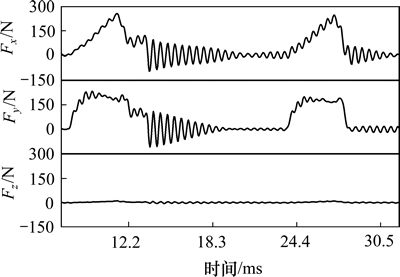
图6  原始切削力信号图

Fig. 6  Original signal diagram of milling forces

图8所示为呈4种典型纤维方向角切削时单齿铣削力时域变化曲线，其切削条件为N=960 r/min，f_z=0.18 mm，其对应的单齿切削时间如表2所示，与式(2)计算值64 ms差异较大。当ψ＝0°时，实际单齿切削时间小于计算值；当ψ＞0°时，实际切削时间大于计算值。

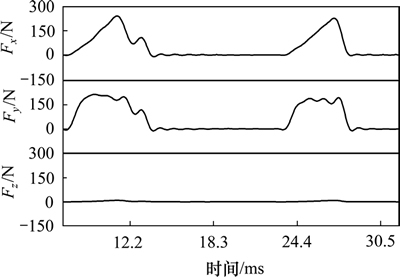
图7  滤波后的三向力信号图

Fig. 7  Filtered signal diagram of milling forces

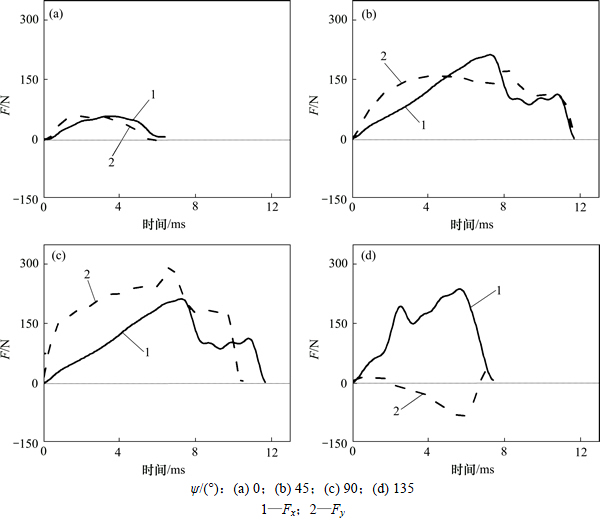
图8  单齿切削信号曲线

Fig. 8  Signal diagram of single edge milling forces

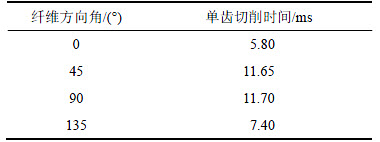
表2  不同纤维方向角下的单齿切削时间

Table 2  Single edge milling time at different fiber orientation angles

当ψ＝0°时，成屑图如图9所示，随着刀具切入工件，在刀具的挤压作用下，纤维与基体的界面出现开裂，同时切削力方向与纤维方向近似平行，开裂将沿着界面向前扩展，形成长条状切屑，当切屑与工件分离后，刀具将出现空切，导致实际单齿切削时间比计算值短。

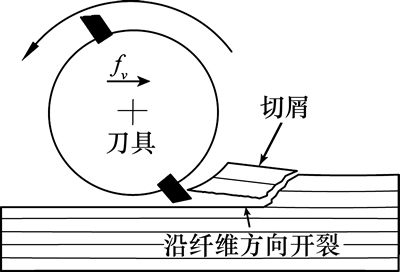
图9  ψ=0°时成屑图

Fig. 9  Chips formation schematic at fiber orientation angle of 0°

当ψ＞0°时，考虑周期性加工使已加工表面产生的波动，导致刀齿与已加工表面发生挤压和刮擦，使刀齿提前进入切削过程，刀齿旋转角增加了△φ，使实际的加工时间比理论计算时间长，如图3所示。根据几何关系可得：

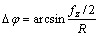                 (4)

使单齿切削时间增加

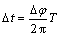                  (5)

计算得

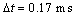                 (6)

从计算结果可以看出，与单齿切削时间相比，△t极小，可见：已加工表面波动并不是导致单齿切削时间变化的主要原因。

当ψ＞0°时，铣削力最大值都出现在6.5 ms左右，即当刀齿即将切出工件时，铣削力取得最大值。假设刀齿切出工件后，切屑与工件分离，则铣削力应瞬时减小为0 N，此时单齿切削时间与计算值相等；但如图6所示，铣削力并没有变为0，而是缓慢减小；而且当ψ＝45°和ψ＝90°时，铣削力曲线出现了另一个尖峰，结合复合材料纤维增强的特点，可以推测这是由于切屑飞离后，纤维回弹与刀具重新作用引起的，由图10可见：刀具切入工件后，工件在刀具作用下弯曲变形，随着变形的持续增大，铣削力达到最大值，随后切屑断裂，从工件飞离，铣削力下降，此时纤维发生回弹，与刀具继续接触，直至刀具与工件分离，从而造成铣削力曲线延长并出现另一个尖峰。

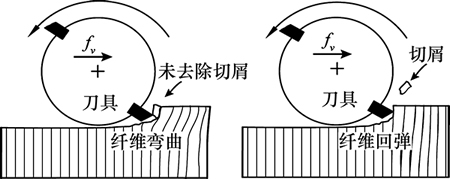
图10  切削过程中纤维回弹

Fig. 10  Schematic diagram of fibers rebounding during cutting process

3.2  显著性分析

使用方差分析，可以得出各因素对铣削力的显著性作用并计算出相应的贡献度，如图11所示。从图11可以看出：纤维方向角是影响铣削力的最重要的因素，其占比达到了84%以上，当纤维方向角变化时，刀具与材料之间的相互作用形式发生改变，引起切削断裂机理的变化，对铣削力造成巨大影响；当纤维方向角相同时，每齿进给量对铣削力有显著的影响，对F_x的影响大，对F_y的影响较小；主轴转速对铣削力影响最小。

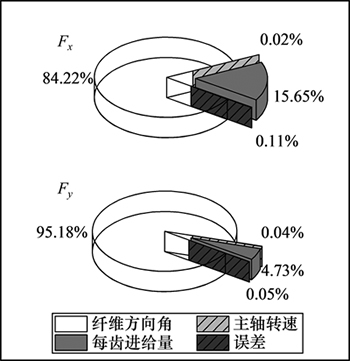
图11  加工参数对铣削力影响结果方差分析

Fig. 11  ANOVA results of cutting parameters

3.3  铣削力随加工参数变化规律

3.3.1  随纤维方向角变化规律

方差分析的结果已经表明：纤维方向角是影响铣削力变化的最主要的因素。图12所示为铣削力随纤维方向角变化曲线，其加工参数为N=960 r/min，f_z=0.18 mm。从图12可以看出：随纤维方向角增大，铣削力先增大后减小，在ψ＝90°时铣削力最大，在ψ＝0°时，铣削力最小；当ψ=135°时，F_y为负值，这与直角切削中结果相同。当ψ=0°时，切屑去除方式以基体开裂为主，而基体界面的强度远远小于纤维强度，铣削力最小^[16]。当ψ=45°及ψ=90°时，纤维主要为直接切断方式，且随纤维方向角增大，未切削材料对切屑的支撑作用逐渐增强，导致铣削力增大^[15]；当ψ=135°时，切削过程中的切屑形成方式与0°时的相似，也是先开裂后弯断的过程，由于ψ＞90°，铣削力沿y方向的分力与其他纤维方向角相反，使F_y出现负值。

3.3.2  随主轴转速变化规律

铣削力随主轴转速变化规律如图13所示，其中f_z= 0.13 mm。从图13可以看出：随主轴转速的增加，F_x和F_y的变化趋势相似，但是不同纤维方向角下的变化规律是不同的。当ψ=0°时，随转速的增加而逐渐增大；当ψ=45°及ψ=135°时，随主轴转速的增加，铣削力缓慢增加；当ψ=90°时，随主轴转速的增加而逐渐减小。

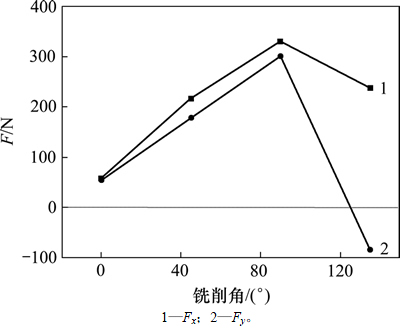
图12  铣削力随纤维方向角变化规律

Fig. 12  Relationships between cutting angle and cutting forces

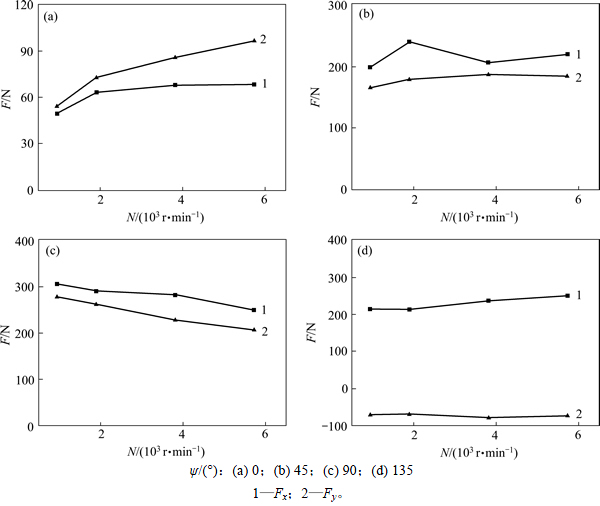
图13  CFRP铣削力随转速的变化规律

Fig. 13  Relationships between spindle speed and cutting forces

由于双直刃铣刀的结构特征，铣削时刀具与材料之间呈断续切削，刀齿与材料之间存在着较为明显的冲击过程，冲击力随着速度的增大而增大；而随着切削速度的增大，切削区温度升高，导致树脂基体软化，对纤维的包裹作用下降，导致铣削力减小；同时随切削速度增大，刀具与材料的摩擦力也将发生变化^[17]；当纤维方向角不同时，3种因素的作用强度发生变化，最终出现如图13所示的变化规律。

3.3.3  随进给量变化规律

图14所示为在N=960 r/min条件下测得的铣削力随每齿进给量的变化规律。可见：随进给量的增加，F_x和F_y的变化趋势相似，且纤维方向角对力的变化趋势影响较小，F_x和F_y均随着每齿进给量的增加而增大。这是由于，随着每齿进给量的增大，刀齿在任意时刻进行切削的切削厚度增加，需要去除的材料体积增大，因此需要克服材料变形所需的力增大。

3.4  单向板铣削力数据获取

BP神经网络采用导师引导学习的方法进行多层次反馈，具有很高的预测精度和较强的泛化能力，近年来在工业工程等方面的应用越来越广泛。KALLA等^{[11, 18-19]}研究表明：对于各向异性、多铺层结构、多加工参数的CFRP多向层合板的铣削力预测，神经网络具有更好的非线性特征，比线性回归法、响应曲面法能达到更高的精度。

3.4.1  归一化处理

采用BP神经网络的方法对CFRP单向层合板的铣削力进行预测，输入是纤维方向角ψ(°)、主轴转速(r/min)和每齿进给量(mm) 3个变量，输出为F_x(N)和F_y(N)，其数值数量级和量纲有较大差异，为了减小输入层数值和量纲对预测模型精度的影响，必须将它们进行归一化(置于[-1，1]的区间内)处理，方法如下：

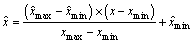       (7)

其中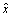：为归一化处理后数值；x为原始输入数值。

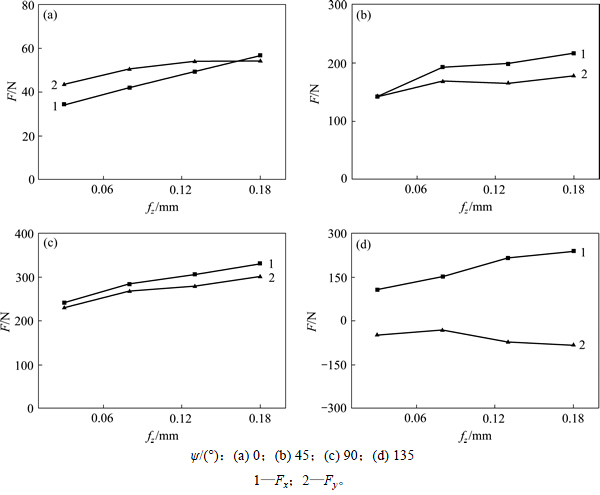
图14  CFRP铣削力随每齿进给的变化规律

Fig. 14  Relationships between feed per tooth and the cutting forces

3.4.2  数据分组

实验共获得64组数据，将其中48组列为训练样本，占比75%，8组为确认样本，占比12.5%，剩余8组为测试样本，占比12.5%，训练样本、确认样本和测试样本的分组随机选取。其中，确认样本是为了防止神经网络的过度拟合而设定的终止迭代条件，设定当确认样本的均方误差连续8次不再下降，则神经网络出现过度拟合的趋势，训练终止。测试样本不参与神经网络的训练过程，是网络生成以后对网络预测精度进行检验的样本。

3.4.3  神经网络的训练和预测

对BP神经网络模型进行创建和训练，设置输入层的神经元数量为3个，输出层神经元的数量为2个，隐藏层的数量设置为5，神经网络的结构如图15所示。传递函数均采用S型正切函数TANSIG，训练函数采用基于Levenberg-Marquadt反传算法(梯度下降法与高斯牛顿法的结合)的TRAINLM，适应性学习函数采用具动量的梯度下降法LEARNGD。设置模型的均方差控制目标为4×10^-5，最终训练结果的均方差值为3.4×10^-4。

使用测试样本对实验结果进行验证，结果表明，神经网络铣削力预测值与实验值的相关系数达到0.987 9，最大相对误差为

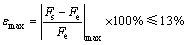      (8)

平均相对误差为

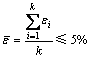              (9)

由此可见，基于BP神经网络建立的单向板铣削力预测模型精确度较高，不同纤维方向角下的神经网络预测值与实验值对比如图16所示。

图15  BP神经网络结构图

Fig. 15  BP neural network configuration

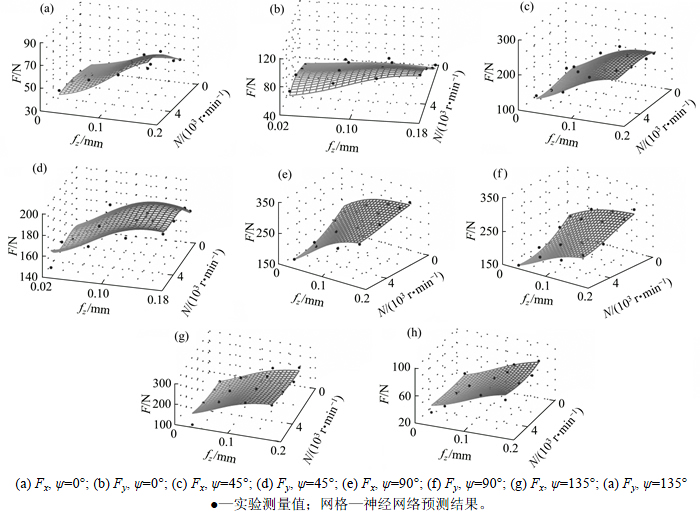
图16  不同纤维方向角下的实验结果与预测值对比

Fig. 16  Comparison of calculated data and test data of unidirectional CFRP at different fiber orientation angles

4  多向层合板铣削力预测

4.1  CFRP多向层合板铣削力模型建立

双直刃铣刀铣削CFRP多向层合板的实质是铣刀的刀齿同时对多个CFRP单向铺层制件进行切削，如图17所示。假设在任意时刻，刀具对同一铺层的铣削力沿刀齿是均匀等值分布的，记f(ψ)为纤维方向角ψ的铺层的单位铣削力，将f(ψ)沿x方向和y方向分解为f_x(ψ)和f_y(ψ)，a_t(ψ)为此方向铺层的厚度，则：

           (10)

为了对上述CFRP多向层合板铣削力叠加计算方法进行验证，需要使用相同的加工参数对CFRP多向层合板和4种典型铺层方向的CFRP单向层合板进行铣削实验，实验参数如表1所示，CFRP多向层合板纤维方向角为：[45, 90, -45, 0]_2S, 90, 90, 90, 90, [45, 90, -45, 0]_2S，则

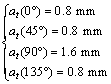           (11)

将16组实验中测得的4种单向层合板的实验信号曲线代入式(10)中得到的计算结果曲线与CFRP多向层合板实际测量曲线比较，可以发现计算结果曲线与实验曲线具有较为相符。图18所示为在N=960 r/min，f_z=0.18 mm，a_e＝1 mm条件下的CFRP多向层合板铣削力计算值与实验值的对比图。从图18可以看出：铣削力计算曲线与实验曲线能较好地符合。因此使用式(10)对CFRP多向层合板板的铣削力进行预测具有可行性。因此，为预测CFRP多向层合板铣削力的最大值，可得

        (12)

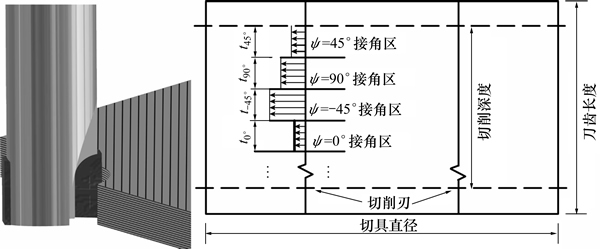
图17  CFRP多向层合板铣削力分析图

Fig. 17  Analysis of multidirectional CFRP milling forces

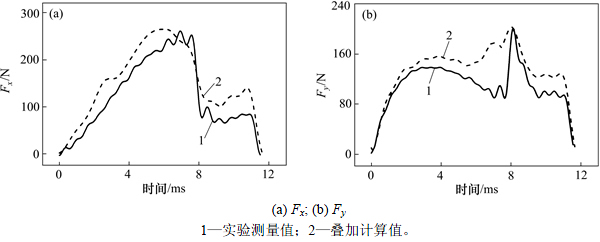
图18  多向板铣削力计算值与实验值对比图

Fig. 18  Comparison of calculated and test data of MDCFRP

考虑到当纤维方向角不同时，出现最大值的时间不同，因此应对不同纤维方向角的铣削力加入优化系数。与其他纤维角度相比，当ψ＝0°时，铣削力的最大值出现较早，因此对CFRP多向层合板的最大值影响较弱，应将其影响系数进行优化。根据最小二乘法将其优化系数调整为0.12，优化后的CFRP多向层合板铣削力预测公式为

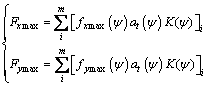      (13)

其中，

                   (14)

4.2  CFRP多向层合板铣削力模型实验验证

为验证预测模型的准确度，选取9组加工参数在2种不同的纤维方向角状态下进行实验，实验结果如图19和图20所示，其中图19中纤维方向角为[45, 90, -45, 90]_2S, 90, 90, 90, 90, [45, 90, -45, 90]_2S，图20中纤维方向角为[-45, 0, 45, 90]_2S, 0, 0, 0, 0,[-45, 0, 45, 90]_2S，代入相对误差计算公式，得

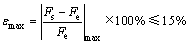     (15)

其中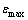：为相对误差最大值；F_s为铣削力预测值；F_e为铣削力实验值。

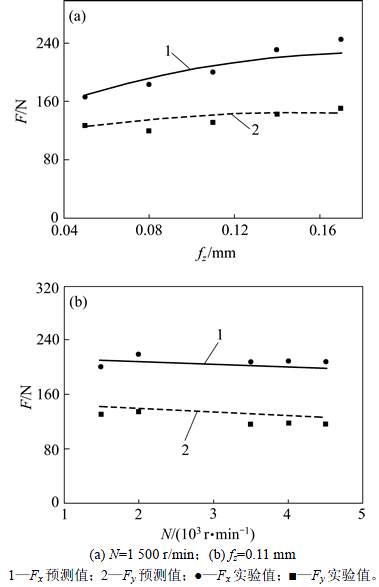
图19  预测值与实验值对比

Fig. 19  Comparison of experiment results and theoretical predictions

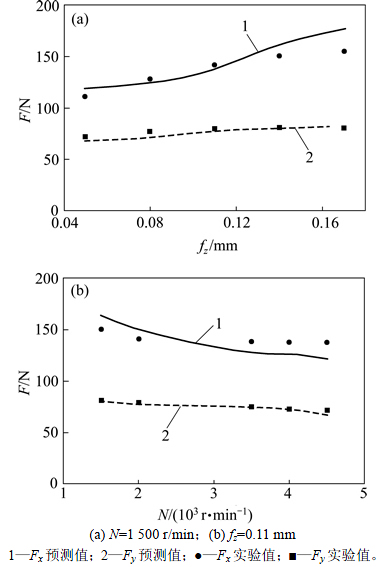
图20  预测值与实验值对比

Fig. 20  Comparison of experiment results and predictions

5  结论

1) 纤维方向角对铣削力影响最大，每齿进给量次之，主轴转速对铣削力影响最小。

2) 基于BP神经网络获取了CFRP单向层合板铣削力，获得了0°~180°纤维方向角内任意CFRP单向层合板铣削力。

3) 研究了CFRP多向层合板铣削力与CFRP单向板之间的关系，建立了从CFRP单向板计算CFRP多向层合板铣削力的模型，并进行了实验验证，模型精度较高并具有通用性。

参考文献：

[1] 康永峰, 陈树巍, 袁士平, 等. 大型碳纤维复合材料壁板轮廓数控铣削工艺技术[J]. 航空制造技术, 2013, 435(15): 70-73.

KANG Yongfeng, CHEN Shuwei, YUAN Shuping, et al. NC milling technology for large carbon fiber composites panel contour[J]. Aeronautical Manufacturing Technology, 2013, 435(15): 70-73.

[2] HAN Shengchao, CHEN Yan, XU Jiuhua, et al. Experimental study of tool wear in milling multidirectional CFRP laminates[J]. Materials Science Forum, 2013, 770: 276-280.

[3] 康永峰, 王文理, 王晓丽. 碳纤维复合材料高速开槽铣削试验研究[J]. 航空制造技术, 2010(22): 82-85.

KANG Yongfeng, WANG Wenli, WANG Xiaoli. Experimental study on high-speed groove-milling of CFRP[J]. Aeronautical Manufacturing Technology, 2010(22): 82-85.

[4] 徐宏海, 徐倩, 刘东. 碳纤维复合材料高速铣削实验研究[J]. 机械设计与制造, 2009(12): 167-169.

XU Honghai, XU Qian, LIU Dong. Experimental study on the high speed milling of carbon fiber reinforced polymer[J]. Machinery Design & Manufacture, 2009(12): 167-169.

[5] K, ZALESKI K. Comparative study in the passive force and cutting torque in the milling process of polymer matrix composites and aluminum alloys[J]. Advances in Science and Technology–Research Journal, 2013, 7(18): 6-12.

[6] SLAMANI M, CHATELAIN J, HAMEDANIANPOUR H. Comparison of two models for predicting tool wear and cutting force components during high speed trimming of CFRP[J]. International Journal of Material Forming, 2015, 8(2): 305-316.

[7] KARPAT Y, BAHTIYAR O, B. Milling force modelling of multidirectional carbon fiber reinforced polymer laminates[J]. Procedia CIRP, 2012, 1(1): 460-465.

[8] KARPAT Y, BAHTIYAR O, B. Mechanistic force modeling for milling of unidirectional carbon fiber reinforced polymer laminates[J]. International Journal of Machine Tools and Manufacture, 2012, 56: 79-93.

[9] KARPAT Y, POLAT N. Mechanistic force modeling for milling of carbon fiber reinforced polymers with double helix tools[J]. CIRP Annals-Manufacturing Technology, 2013, 62(1): 95-98.

[10] 韩胜超, 陈燕, 徐九华, 等. 多齿铣刀侧铣加工多层CFRP铣削力的建模与仿真[J]. 复合材料学报, 2014, 31(5): 1375-1381.

HAN Shengchao, CHEN Yan, XU Jiuhua, et al. Modeling and simulation of milling forces in side milling multi-layer CFRP with multitooth cutter[J]. Acta Materiae Compositae Sinica, 2014, 31(5): 1375-1381.

[11] KALLA D, SHEIKH-AHMAD J, TWOMEY J. Prediction of cutting forces in helical end milling fiber reinforced polymers[J]. International Journal of Machine Tools and Manufacture, 2010, 50(10): 882-891.

[12] KALLA D K. Committee neural network force prediction model in milling of fiber reinforced polymers[D]. Kansas: Wichita State University. Department of Industrial and Manufacturing Engineering, 2008: 1-199.

[13] SHEIKH-AHMAD J, TWOMEY J, KALLA D, et al. Multiple regression and committee neural network force prediction models in milling FRP[J]. Machining Science and Technology, 2007, 11(3): 391-412.

[14] WANG D H, RAMULU M, AROLA D. Orthogonal cutting mechanisms of graphite/epoxy composite, Part Ⅱ: multi-directional laminate[J]. International Journal of Machine Tools and Manufacture, 1995, 35(12): 1639-1648.

[15] 贾振元, 宿友亮, 张博宇, 等. 基于径向基函数神经网络的碳纤维增强树脂基复合材料切削力预测[J]. 复合材料学报, 2015, 33(3): 516-524.

JIA Zhenyuan, SU Youliang, ZHANG Boyu. The prediction of the cutting force in machining CFRP based on the RBF artificial neural network[J]. Acta Materiae Compositae Sinica, 2015, 33(3): 516-524.

[16] WANG D H, RAMULU M, AROLA D. Orthogonal cutting mechanisms of graphite/epoxy composite, Part Ⅰ: Unidirectional laminate[J]. Machine Tools Manufacture, 1995, 35(12): 1623-1638.

[17] KLINKOVA O, RECH J, DRAPIER S, et al. Characterization of friction properties at the workmaterial/cutting tool interface during the machining of randomly structured carbon fibers reinforced polymer with carbide tools under dry conditions[J]. Tribology International, 2011, 44(12): 2050-2058.

[18] KARNIK S R, GAITONDE V N, RUBIO J C, et al. Delamination analysis in high speed drilling of carbon fiber reinforced plastics (CFRP) using artificial neural network model[J]. Materials & Design, 2008, 29(9): 1768-1776.

[19] TSAO C C. Comparison between response surface methodology and radial basis function network for core-center drill in drilling composite materials[J]. The International Journal of Advanced Manufacturing Technology, 2008, 37(11/12): 1061-1068.

(编辑  赵俊)

收稿日期：2016-12-24；修回日期：2017-01-21

基金项目(Foundation item)：国家重点基础研究发展计划(973计划)项目(2014CB046503)；国家自然科学基金资助项目(51575082，U1508207，51621064)；中央高校基本科研业务费专项资金资助项目(DUT16TD01) (Project(2014CB046503) supported by the National Basic Research Development Program (973 Program) of China; Projects(51575082, U1508207, 51621064) supported by the National Natural Science Foundation of China; Project(DUT16TD01) supported by the Fundamental Research Funds for the Central Universities)

通信作者：王福吉，博士，教授，从事复合材料切削原理与工具设计研究；E-mail: wfjsll@dlut.edu.cn