超声波在引线键合机变幅杆中的传递规律

王福亮, 李军辉, 韩 雷, 钟 掘

(中南大学 机电工程学院, 湖南 长沙, 410083)

摘要: 基于解析模型的方法, 研究了超声波在热超声金丝球引线键合机变幅杆中的传递规律。 在忽略变幅杆横向惯性效应, 假定线弹性、 无阻尼情况下, 考虑变幅杆纵向微小振动, 从一维变截面杆振动方程出发, 建立热超声金丝球引线键合机复合变幅杆的动力学方程, 推导它的频率方程, 获得各阶振型。 研究结果表明: 在变幅杆的各阶振型中, 两端都是位移腹点, 但是幅值不同, 这也是变幅杆可以传递超声波的原因; 夹持器应只有位于位移节点, 才能为变幅杆系统提供支撑的同时不对超声波传递产生影响。

关键词: 超声波; 变幅杆; 引线键合

中图分类号:TG453⁺.9 文献标识码:A 文章编号: 1672-7207(2005)06-1017-04

Ultrasonic transfer on horn of wire bonder

WANG Fu-liang, LI Jun-hui, HAN Lei, ZHONG Jue

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract: Based on the analysis model, the ultrasonic transfer on the horn of wire bonder was studied. A dynamics equation of the composite transducer is established by the vibration equation of one dimension section changed pole, based on the following: the radial direction inertia and damping was ignored; the material was liner elastic; only the axis direction micro-vibration was considered. The frequency equation and vibration model were also deduced. The results show that the ends of the transducer are always the maximum displacement positions, but the amplitudes are different, and this is the reason why the horn can transfer ultrasonic. The holder should be located on the node of the horn, so that it can support the transducer system and have no effect on the ultrasonic transfer.

Key words: ultrasonic wave; horn; wire bonding

超声波是一种机械波, 在微电子封装领域中被广泛应用于热超声金丝球引线键合(Thermosonic golden ball wire bonding)、 超声楔键合(Ultrasonic wedge bonding)和热超声倒装(Thermosonic flip chip)。 在这些应用中, 变幅杆是超声波传递和聚集的部件, 研究超声波在变幅杆中的传递具有重要意义。 其研究方法可归纳为3类:

a. 基于力电类比原理^[1-3]。 该方法因其可将复杂的机械振动问题转化为熟知的交流电路, 显得较简单而被广泛使用; 其缺点是只能处理集中参数振动系统, 对于复杂分布参数振动系统不能精确求解。

b. 基于有限元^[4-7]。 该方法可精确建立并求解复杂分布参数振动系统模型, 但是, 难以确定决定系统的关键因素以及其相互影响规律。

c. 基于解析模型^[8-14]。 该方法试图通过建立系统的动力学方程并确定边界条件以了解超声波在变幅杆中的传递规律; 虽然要忽略一些系统细节, 却能准确确定决定系统的关键因素。 相比较而言, 基于解析模型的方法最有利于了解超声波在变幅杆中的传递规律。 关于变幅杆的研究大多针对一般工业用超声波加工, 如超声切割、 珩磨、 拉拔等, 与微电子封装中的超声波应用相比, 其精度与加载形式都有较大区别。 在此, 作者利用解析模型的方法, 研究超声波在热超声金丝球引线键合机变幅杆中的传递规律。

1 引线键合机换能器系统

微电子封装中超声引线键合机的功能是: 在常温环境下, 通过超声振动和劈刀压力的作用, 将金丝(直径一般为0.025 mm)焊接到IC焊盘和基板引脚上, 将IC与基板的电路连接在一起^[1]。 其中, 换能器是键合机的核心部件, 其结构如图1所示。 其工作原理为: 超声发生电路发出超声频率的电信号驱动PZT; PZT将电信号转换成同频率的纵向超声波, 经变幅杆传递放大后, 在劈刀中改变方向, 转换为横向超声波振动, 最后, 作用在金丝和芯片之焊盘间工作界面上, 将金丝焊接在焊盘上, 完成超声引线键合的功能。

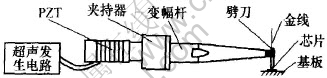
图 1   引线键合机换能器的结构

Fig. 1   Transducer structure of wire bonder

超声波能量从PZT到键合界面的传递过程中, 变幅杆是一个重要的环节。 分析其固有特性, 是分析并改进热超声引线键合机设计的基础。

本文研究的对象是U2100热超声金丝球引线键合机(由深圳微讯自动化设备有限公司制造)的变幅杆, 其结构及几何尺寸如图2所示。

该变幅杆具有以下特征:

a. 横截面为圆形, 由各向同性的钢制成(超声波纵波速约5km/s); 总长l=82.7 mm, 由3段连接而成(l₁=39.2 mm, l₂=40 mm, l₃=3.5 mm), 左、 右两段是等截面的PZT加载端(大端)和劈刀负载端, 直径分别为D₁=10.5 mm, D₂=3.5 mm; 中间段为过渡变截面杆。 这种设计一方面使变幅杆具有较大的放大系数, 另一方面使得变幅杆具有较大的刚度, 可承受较大载荷。

b. 变幅杆中靠近PZT加载端处的肋环及夹持器(直径分别为18.8 mm和19 mm)提供整个结构静动态支撑。

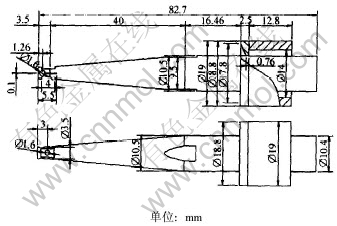
图 2   引线键合机变幅杆几何尺寸

Fig. 2   Size of wire bonder horn

2 变幅杆的动力学方程及其求解

对图2所示的变幅杆建立精确的动力学模型无疑是非常困难的, 为此, 要忽略部分细节, 即将其肋环、 夹持器、 中部的定位平面及劈刀负载端的开槽和开孔忽略。 其几何构形如图3所示。

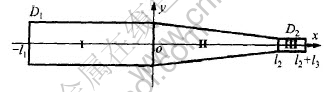
图 3   简化后的变幅杆

Fig. 3   Simplified horn

在变幅杆上建立如图3所示坐标系统, 定义大端段为第Ⅰ段, 过渡段为第Ⅱ段, 小端段为第Ⅲ段, 忽略变幅杆的横向惯性效应, 在假定线弹性、 无阻尼条件下考虑其纵向微小振动, 可得一维变截面杆的振动方程^{[9, 10]}:

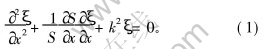
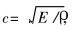其中: S=S(x), 为变幅杆截面积函数; ξ=ξ(x), 为杆中质点的位移分布方程; , k为圆波数, ω为圆频率; , 为纵波在细棒中的传播速度。 方程(1)的通解形式为:

ξ=a₁coskx+a₂sinkx。(2)

其中: a₁和a₂由边界条件确定。 根据变幅杆各段的截面积函数和边界条件, 可得各段杆中质点的自由振动振型位移分布为:

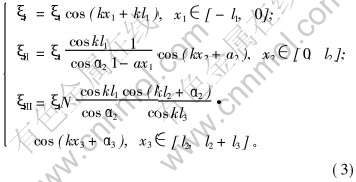
其中: α₁=kl₁; tanα₂=tankl₁+α/k; α₃=-(kl₂+kl₃);  为截面积系数; ξ₁为变幅杆的输入振幅; k=2πf/c_L, 为圆波数; f是超声发生器的激励频率; c_L为纵波在变幅杆中的传播速度; l₁=39.2 mm; l₂=40 mm; l₃=3.5 mm; D₁=10.5 mm; D₂=3.5 mm。

3 变幅杆的稳态振型及频率方程

由变幅杆两端自由的边界条件, 可求得其固有频率方程为:

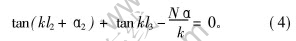
代入变幅杆的几何和力学参数, 求解式(4), 可得到前3阶固有频率分别为: 39.9, 66.86和98.27 kHz。 将各阶固有频率及参数代入式(3)可得到相应振型, 如图4所示。

由图4可知, 变幅杆的各阶振型中, 两端是位移/速度腹点, 这也正是变幅杆能传递并放大超声波振动的原因; 然而, 在不同的振型中, 左右两端的振幅比不一样, 在相同的输入振幅情况下, 高频的振型具有较大的输出振幅。 此外, 每阶振型都存在节点; 当夹持器位于节点位置时, 一方面, 可使得超声波在穿过夹持器时不会有振幅衰减; 另一方面, 使得变幅杆有1个支点, 可以承受来自工作界面的力和力矩, 且不改变变幅杆系统的边界条件, 这种稳定的系统特性对于精细的引线键合工艺来说是非常重要的。

热超声金丝球引线键合机的工作频率为60 kHz, 经计算可知第一个节点出现在距大端21.667 mm处, 实际节点位置(即夹持器位置)距大端约21 mm, 其中误差可能源自推导时简化了变幅杆细节, 忽略了夹持器厚度对超声波传递的影响。

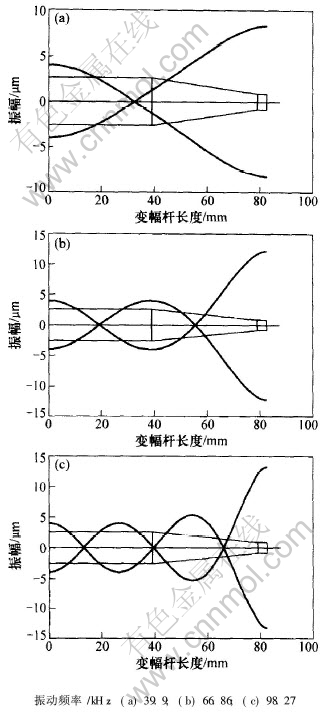
图 4   变幅杆中超声波的传递规律

Fig. 4   Ultrasonic transfer regular on horn

4 结 论

a. 在忽略变幅杆的横向惯性效应、 假定线弹性、 无阻尼情况下, 考虑其纵向微小振动, 从一维变截面杆的振动方程出发, 建立了复合变幅杆的动力学方程, 推导了它的频率方程, 求解了稳态振动的模态, 获得了各阶振型。 在变幅杆的各阶振型中, 两端都是位移腹点, 但是幅值不同, 这也是变幅杆可以传递超声波的原因。

b. 夹持器应位于位移节点, 才能为变幅杆系统提供支撑的同时不致对超声波传递产生影响。

c. 变幅杆细节的简化将导致计算特征参数时一定的误差。 因此, 在设计变幅杆时, 可考虑在解析模型计算的基础上采用有限元方法, 进行精确分析。

参考文献:

[1]贺西平, 程存弟.纵振型超声变幅杆的等效四端网络[J], 陕西师范大学学报(自然科学版) 1994, 22(1): 87-88.

HHE Xi-ping, CHEN Cun-di. Equivalent four-terminal networks of the longitudinal ultrasonic horns[J], Journal of Shanxi Normal University(Natural Science Edition), 1994, 22(1): 87-88.

[2]梁召峰, 林书玉.余弦形过渡段阶梯形变幅杆研究[J]. 陕西师范大学学报(自然科学版).2003, 31(4): 32-35.

LIANG Zhao-feng, LIN Shu-yu. Study of step horn with cosine type transition[J]. Journal of Shanxi Normal University(Natural Science Edition), 2003, 31(4): 32-35.

[3]赵福令, 冯冬菊, 郭东明, 等. 超声变幅杆的四端网络法设计[J]. 声学学报, 2002, 27(6): 554-558.

ZHAO Fu-ling, FENG Dong-ju, GUO Dong-ming, et al. Design of horn using four-end network method[J]. Acta acustica, 2002, 27(6): 554-558.

[4]万德安, 刘春节. 超声变幅杆的模态分析[J]. 机械与电子, 2004, 21(4): 10-12.

WAN De-an, LIU Chun-Jie. Modal analysis of ultrasonic amplitude amplifier pole[J]. Machine and Electronic, 2004, 21(4): 10-12.

[5]原丰霞, 张慧君, 朱国良. 基于ANSYS的超声变幅杆的优化设计[J]. 机械工程师, 2004, 12(11): 24-26.

YUAN Feng-xia, ZHANG Hui-jun, ZHU Guo-liang. Optimum design of acoustic horus for ultrasonic machining using ANSYS[J]. Mechanical Engineer, 2004, 12(11): 24-26.

[6]赖一楠, 刘向东, 罗建伟, 等. 级联式变幅杆有限元分析[J]. 哈尔滨理工大学学报, 2001, 6(1): 50-53.

LAI Yi-nan, LIU Xiang-dong, LUO Jian-wei, et al. Analyzing ultrasonic horn system by finite element method[J]. Journal of Harbin Institute of Technology, 2001, 6(1): 50-53.

[7]刘井权, 闫久春, 杨士勤. 超声刀切割系统的模态分析[J]. 哈尔滨工业大学学报, 2001, 33(4): 435-438.

LIU Jing-quan, YAN Jiu-chun, YANG Shi-qin. Model analysis of ultrasonic knife cutting system[J]. Journal of Harbin Institute of Technology, 2001, 33(4): 435-438.

[8]钟美鹏. 超声珩磨系统中指数变幅杆的设计与研究[J]. 机电工程, 2003, 20(3): 54-56.

ZHONG Mei-peng. Study and designing on the exponent type amplitude-changed bar in the ultrasonic honing system[J]. Mechanical and Electrical Engineering Magazine, 2003, 20(3): 54-56.

[9]王敏慧, 鲍善惠, 江长青. 粗细端不等长阶梯形变幅杆谐振频率的实验研究[J]. 陕西师范大学学报(自然科学版), 2004, 32(3): 47-49.

WANG Ming-hui, BAO Shan-hui, JIANG Chang-qing. Experiment study on the resonance frequency of step horn with difference length on the big and small ends[J]. Journal of Shanxi Normal University(Natural Science Edition), 2004, 32(3): 47-49.

[10]刘世清, 林书玉. 扭转超声振动系统中局部共振的研究[J]. 应用声学.2004, 23(2): 11-14.

LIU Shi-qing, LIX Shu-yu. Study on the local resonance in torsional ultrasonic vibration systems[J]. Applied Acoustics, 2004, 23(2): 11-14.

[11]贺西平. 一端带有圆柱杆的复合纵振超声变幅杆的简明设计理论[J]. 声学技术, 1994, 13(2): 85-88.

HE Xi-ping. Concise design theory of complex longitudinal ultrasonic horn with cylinder pole at one end[J]. Acoustics Technology, 1994, 13(2): 85-88.

[12]石健滨, 耿雪霏, 于海波. 超声处理复合材料界面中变幅杆的设计[J]. 黑龙江工程学院学报, 2001, 15(4): 7-9.

SHI Jian-bin, GENG Xue-fei, YU Hai-bo. Design of cascade horn of ultrasonic processing in the interface of composite material[J]. Journal of Heilongjiang Institute of Technology, 2001, 15(4): 7-9.

[13]林仲茂.超声变幅杆的原理和设计[M].北京: 科学出版社, 1987.

LIN Zhong-mao. Theory and Design of Ultrasonic Horn[M]. Beijing: Science Press, 1987.

[14]张云电.超声加工及其应用[M].北京: 国防工业出版社, 1995.

ZHANG Yun-dian. Ultrasonic Process and it′s Application[M]. Beijing: National Defence Industry Press, 1995.

收稿日期:2005-05-06

基金项目: 国家自然科学基金重大项目(50390064); 国家重点基础研究发展计划(“973”计划)项目(2003CB716202)

作者简介:王福亮(1979-), 男, 湖南宜章人, 博士研究生, 从事微电子封装技术与装备研究

论文联系人: 王福亮, 男, 博士研究生; 电话: 0731-8879044(O); E-mail: wangfuliang@mail.csu.edu.cn