非线性破坏准则下浅埋隧道围岩压力的极限分析
杨小礼,王作伟
(中南大学 土木建筑学院,湖南 长沙,410075)
摘 要:采用土体非线性破坏准则,基于浅埋隧道的泰沙基破坏模式,利用极限分析法中的上限定理,推导非线性破坏准则下浅埋隧道围岩压力的计算公式。运用序列二次规划算法进行优化分析,得出围岩压力上限解的最优值。研究结果表明:当非线性系数m=1时,非线性破坏准则变成线性Mohr-Coulomb准则,本文方法的计算结果与泰沙基极限平衡法的计算结果比较接近,证明了本文方法的有效性;非线性系数对围岩压力上限解有较明显的影响。
关键词:非线性破坏准则;浅埋隧道;围岩压力;上限定理
中图分类号:TU91 文献标志码:A 文章编号:1672-7207(2010)01-0299-04
Limit analysis of earth pressure on shallow tunnel using nonlinear failure criterion
YANG Xiao-li, WANG Zuo-wei
(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract: Based on the known failure mechanism, the upper bound theory was applied to derive the expression of earth pressure on shallow tunnel. The upper bound solutions of earth pressure were obtained by using the nonlinear sequential quadratic programming algorithm. The results show that the upper bound solutions approximate the previously solutions when the nonlinear failure criterion reduces to linear Mohr-Coulomb criterion. The failure mechanism is feasible to limit analysis. Nonlinear coefficient has significant influence on the upper bound solution of earth pressure of shallow tunnels.
Key words: nonlinear failure criterion; shallow tunnel; earth pressure; upper bound theorem
围岩是指隧道开挖后其周围产生应力重新分布的岩土体,或指隧道开挖后对其稳定性能产生影响的土体[1]。隧道开挖后,因围岩变形、松弛等,作用于隧道支护或衬砌结构上的压力称为围岩压力。对于浅埋隧道,围岩压力的计算方法主要有土柱理论、泰沙基极限平衡法及铁路、公路隧道设计规范所推荐的方 法[1-2],这些方法都是根据极限平衡理论求解。随着极限分析理论在土压力、边坡稳定以及地基承载力等岩土工程领域中的不断发展[3-6],国内外一些学者将极限分析理论应用于隧道围岩稳定性分析,如:Atkinson等[7]利用极限分析上、下限定理和模型试验方法分析了无黏性土浅埋隧道稳定性问题;Davis等[8]根据上限定理,假定了4种不同的破坏模式,对黏性土在不排水条件下的浅埋隧道围岩稳定性进行了分析;Leca 等[9]利用上、下限定理,研究了浅埋隧道工作面的三维稳定性问题;姜功良[10]应用极限分析有限元方法求解隧道的稳定系数,改善了上限分析结果。以上浅埋隧道稳定性研究是基于土体线性破坏准则。然而,研究表明[11-14]:多数土体服从非线性破坏准则,线性破坏准则只是其中一个特殊情况。非线性破坏准则在岩土工程中已经得到广泛应用[15-17]。在土体非线性破坏准则下,本文作者运用极限分析上限定理,根据泰沙基破坏模式,计算浅埋隧道围岩压力的上限解。
1 基本原理
1.1 非线性破坏准则
根据文献[17],土体非线性破坏准则可表达为:
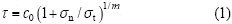
其中:σn和τ分别为破坏面上的正应力和剪应力;c0为初始黏聚力;σt为轴向拉应力;m为非线性系数。c0,σt及m可以由实验得到。当m=1时,式(1)变为线性Mohr-Coulomb破坏准则的表达式。非线性破坏准则式(1)的切线方程为:
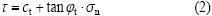
其中:ct和tan φt分别表示切线的斜率和截距。联立式(1)和(2)得ct的表达式为:
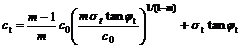 (3)
(3)
根据切线法原理[15]可知,由式(2)和(3)求出的上限解必定是非线性关系式(1)的上限解。
1.2 极限分析上限定理
极限分析法建立在虚功率原理基础上。虚功率原理表明:对于理想的土体,任意一组静力容许的应力场和任意一组机动容许位移速度场,外力的虚功率等于物体所能接受的虚变形功率。在虚功率原理的基础上可推导出上限定理为:在所有的机动容许的塑性变形速度场相对应的荷载中,极限荷载最小[3]。
2 破坏模式与速度场
泰沙基理论[18]是基于极限平衡法计算隧道围岩压力的,其破坏模式如图1所示。本文将其应用到极限分析法中,假定隧道顶板与边墙的支护反力均分布均匀。顶板以上矩形块ABB1A1的移动速度为v0,方向竖直向下;边墙处三角形块移动速度为v1,其相对速度为v01。根据相关联流动法则,刚性块之间速度间断线上的速度矢量方向与间断线夹角为φt,且各速度矢量满足矢量闭合条件,从而得到破坏模式对应的速度场,如图2所示。
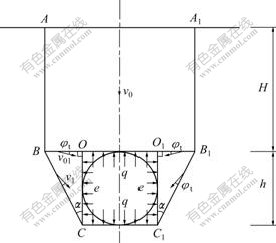
图1 极限平衡破坏模式
Fig.1 Limit equilibrium failure mechanism

图2 与破坏模式相对应的相容速度场
Fig.2 Velocity hodograph corresponding to above
failure mechanism
3 围岩压力计算
3.1 速度关系
根据刚性块应满足运动许可条件及图2,可得v0,v1和v01之间的关系如下:
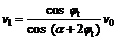 (4)
(4)
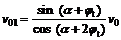 (5)
(5)
3.2 外力功率
浅埋隧道发生破坏时,外力功率包括土体重力功率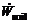 和支护反力所产生的功率
和支护反力所产生的功率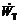 。考虑到问题的对称性,外力功率和内部能量耗散均只计算一半。
。考虑到问题的对称性,外力功率和内部能量耗散均只计算一半。
3.2.1 重力功率
土体重力功率的一半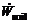 可以分为
可以分为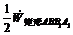 和
和 2部分进行计算,最后将其叠加。计算过程如下。
2部分进行计算,最后将其叠加。计算过程如下。
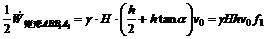
(6)
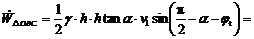
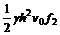 (7)
(7)
所以,
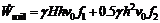 (8)
(8)
3.2.2 支护反力功率
隧道顶板竖向支护反力q和边墙水平支护反力e所做功率之和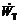 为:
为:
 (9)
(9)
其中:e=Kq;K为待定参数。
3.3 内部能量耗散率
内能耗散的一半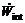 等于速度间断线OB和BC上的能量耗散之和,计算式如下:
等于速度间断线OB和BC上的能量耗散之和,计算式如下:
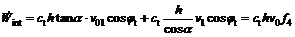 (10)
(10)
3.4 围岩压力q
根据虚功率原理,外力做功与内部耗散能量相等,得竖向支护反力q的表达式:
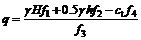 (11)
(11)
其中,f1~f4是关于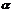 和
和 的无量纲函数,其表达式为:
的无量纲函数,其表达式为:
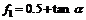 ;
;
 ;
;
 ;
;
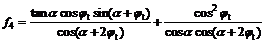 。
。
4 数值计算与分析
4.1 上限解的优化
由式(11)可知,当其他参数一定时,由1组角度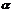 和
和 可以完全确定其破坏形状,同时对应1个上限解。于是,问题转化为:在满足物理意义的约束条件下,寻求目标函数
可以完全确定其破坏形状,同时对应1个上限解。于是,问题转化为:在满足物理意义的约束条件下,寻求目标函数 的最大值。由图2可知破坏模式对应的约束条件为:
的最大值。由图2可知破坏模式对应的约束条件为:
 (12)
(12)
 (13)
(13)
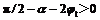 (14)
(14)
在约束条件(12)~(14)下,不断调整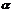 和
和 ,然后,代入式(11),得出最大q,即为优化上限解。此过程可以运用序列二次规划算法,通过Matlab软件编程来 实现。
,然后,代入式(11),得出最大q,即为优化上限解。此过程可以运用序列二次规划算法,通过Matlab软件编程来 实现。
4.2 对比分析
对于浅埋隧道,可据泰沙基理论确定围岩压力[18]:
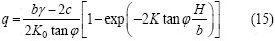
其中:K0为隧道上方岩土层侧压力系数。泰沙基[18]根据实验结果建议K0取1.0~1.5。b为地表面到拱顶的滑动地块的宽度,
 (16)
(16)
取隧道埋深H=20 m,隧道跨度h=10 m,围岩容重γ=20 kN/m3,内摩擦角φ=18?,黏聚力c=10.0 kPa。根据式(15)~(16)可以计算围岩压力q,结果见表1。在线性破坏准则下,即当m=1.0时,取K=0.40~0.65,按本文极限分析方法计算得出围岩压力q,如表1所示,其中:q0为用泰沙基极限平衡法所得的围岩压力。
表1 泰沙基法与本文方法计算结果比较
Table 1 Comparisons of calculation results between limit equilibrium solutions and present solutions
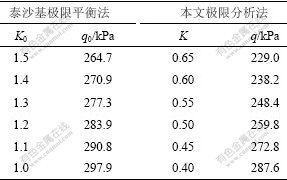
从表1可看出,采用本文方法所得结果与采用泰沙基法所得结果比较接近,说明本文极限分析方法是可行的。
4.3 非线性破坏准则的影响
取隧道埋深H=20 m,隧道跨度h=10 m,围岩容重γ=20 kN/m3,黏聚力c=10.0 kPa,拉应力σt=30 kPa。在非线性破坏准则下,取m=1.1~1.4,计算泰沙基破坏模式下的围岩压力上限解,结果如表2所示。
表2 非线性破坏准则下的围岩压力及破裂角
Table 2 Results of break angles and earth pressures using different nonlinear factors
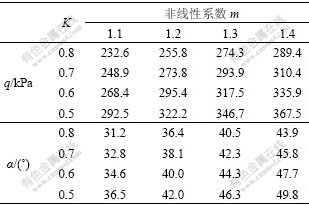
由表2可以看出:当K一定时,随着非线性系数m的增大,围岩压力q和破裂角α均有增大的趋势。因此,在土体服从非线性破坏准则时,如何准确地确定非线性系数对于围岩压力的计算有重要作用。当K=0.8,m取1.1~1.4时,绘制出经过优化的破坏模式,如图3所示。
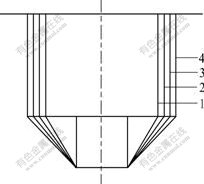
m: 1—1.1; 2—1.2; 3—1.3; 4—1.4
图3 非线性系数对浅埋隧道破坏模式的影响
Fig.3 Influence of nonlinear factor on failure mechanism by optimization
5 结论
(1) 根据极限分析方法中的上限定理计算浅埋隧道围岩压力时,泰沙基破坏模式是适用的。
(2) 在非线性破坏准则下,根据极限分析上限定理,推导出浅埋隧道围岩压力的计算公式,并计算出围岩压力的最优解。
(3) 非线性系数m对围岩压力的上限解有明显的影响。随着m的增加,围岩压力呈非线性增大趋势。
参考文献:
[1] TB 10003—2001, 铁路隧道设计规范[S].
TB 10003—2001, Code for design of railway tunnel[S].
[2] JTG D70—2004, 公路隧道设计规范[S].
JTG D70—2004, Code for design of road tunnel[S].
[3] Chen W F. Limit analysis and soil mechanics[M]. New York: Elsevier Scientific Publishing Company, 1975.
[4] Soubra A H, Regenass P. Three-dimensional passive earth pressures by kinematical approach[J]. Journal of Geotechanical and Geoenvironmental Engineering, 2001, 126(11): 969-978.
[5] Donald I, Chen Z Y. Slope stability analysis by the upper bound approach: fundamentals and methods[J]. Canadian Geotechnical Journal, 1997, 34(6): 853-851.
[6] Wang Y J, Yin J H, Chen Z Y. Calculation of bearing capacity of a strip footing using an upper bound method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(8): 841-851.
[7] Atkinson J H, Potts D M. Stability of shallow tunnel in cohesionless soil[J]. Geotechnique, 1977, 27(2): 203-215.
[8] Davis E H, Gunn M J, Mair R J. The stability of shallow tunnel and underground openings in cohesive material[J]. Geotechnique, 1980, 30(4): 397-416.
[9] Leca E, Dormieux L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J]. Geotechnique, 1990, 40(4): 581-606.
[10] 姜功良. 浅埋软土隧道稳定性极限分析[J]. 土木工程学报, 1998, 31(5): 65-72.
JIANG Gong-liang. Limit analysis of the stability of shallow tunnels in soft ground[J]. China Civil Engineering Journal, 1998, 31(5): 65-72.
[11] Lade P V. Elasto-plastic stress-strain theory for cohesionless soil with curved yield surface[J]. International Journal of Solids Structure, 1977, 13: 1019-1035.
[12] Hoek E, Brown E. Empirical strength criterion for rock masses[J]. Journal of Geotechnical Engineering Division, 1980, 106(9): 1013-1035.
[13] Agar J G, Morgenstern N R, Scott J. Shear strength and stress-strain behavior of Athabasca oil sand at elevated temperatures and pressure[J]. Canadian Geotechnical Journal, 1985, 24(1): 1-10.
[14] Santarelli F. Theoretical and experimental investigation of the stability of the axisymmetric borehole[D]. London: University of London, 1987.
[15] YANG Xiao-Li, YIN Jian-Hua. Estimation of seismic passive earth pressures with nonlinear failure criterion[J]. Engineering Structures, 2006, 28(3): 342-348.
[16] YANG Xiao-Li. Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion[J]. Theoretical and Applied Fracture Mechanics, 2007, 47(1): 46-56.
[17] Zhang X J, Chen W F. Stability analysis of slopes with general nonlinear failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33-50.
[18] 樗木武. 隧道力学[M]. 关宝树, 麦倜曾, 译. 北京: 中国铁道出版社, 1983.
CHU Mu-wu. Tunnel mechanics[M]. GUAN Bao-shu, MAI Ti-zeng, trans. Beijing: China Railway Press, 1983.
收稿日期:2008-12-05;修回日期:2009-03-05
基金项目:全国百篇优秀博士学位论文基金资助项目(2005050);湖南省自然科学基金资助项目(09JJ1008)
通信作者:杨小礼(1970-),男,安徽安庆人,博士,教授,从事交通基础工程的教学与科研工作;电话:0731-82656248;E-mail: yangxl@mail.csu.edu.cn
(编辑 陈灿华)