J. Cent. South Univ. (2019) 26: 3397-3409

DOI: https://doi.org/10.1007/s11771-019-4262-9

Mechanical properties of bimrocks with high rock block proportion

LIN Yue-xiang(林越翔)¹, PENG Li-min(彭立敏)¹, LEI Ming-feng(雷明锋)^{1, 2},YANG Wei-chao(杨伟超)¹, LIU Jian-wen(刘建文)¹

1. School of Civil Engineering, Central South University, Changsha 410075, China;

2. Key Laboratory of Engineering Structure of Heavy Haul Railway (Central South University),Changsha 410075, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: For the investigation of mechanical properties of the bimrocks with high rock block proportion, a series of laboratory experiments, including resonance frequency and uniaxial compressive tests, are conducted on the 64 fabricated bimrocks specimens. The results demonstrate that dynamic elastic modulus is strongly correlated with the uniaxial compressive strength, elastic modulus and block proportions of the bimrocks. In addition, the density of the bimrocks has a good correlation with the mechanical properties of cases with varying block proportions. Thus, three crucial indices (including matrix strength) are used as basic input parameters for the prediction of the mechanical properties of the bimrocks. Other than adopting the traditional simple regression and multi-regression analyses, a new prediction model based on the optimized general regression neural network (GRNN) algorithm is proposed. Note that, the performance of the multi-regression prediction model is better than that of the simple regression model, owing to the consideration of various influencing factors. However, the comparison between model predictions indicates that the optimized GRNN model performs better than the multi-regression model does. Model validation and verification based on fabricated data and experimental data from the literature are performed to verify the predictability and applicability of the proposed optimized GRNN model.

Key words: block-in-matrix-rock; high rock block proportion; resonance frequency test; general regression neural network

Cite this article as: LIN Yue-xiang, PENG Li-min, LEI Ming-feng, YANG Wei-chao, LIU Jian-wen. Mechanical properties of bimrocks with high rock block proportion [J]. Journal of Central South University, 2019, 26(12): 3397-3409. DOI: https://doi.org/10.1007/s11771-019-4262-9.

1 Introduction

Geological mixtures of significant blocks and a bonded matrix of fine texture, such as volcanic agglomerates, fault breccia, and coarse pyroclastic rocks, are problematic geological masses for construction of engineering structures due to their complexity, anisotropy and heterogeneity [1-5]. MEDLEY et al [6] fabricated bimrocks, which is the abbreviation of block-in-matrix rocks, to describe these kinds of geological mixtures.

Various underground and surface structures have been built on or within these complicated geological mixtures with the rapid development of urbanization. Thus, studies on characteristic and mechanical properties of the bimrocks have drawn considerable attention in the past few decades [7-11]. As known, UCS and elastic modulus are crucial mechanical properties for evaluating strength and deformation behaviors of geological masses during the design stage of engineering structures. Thus, determination of UCS and elastic modulus of the bimrocks based on their physical characteristics, such as volumetric block proportion (VBP), density, transonic pulse velocity, and acoustic emission, is a fundamental topic for the bimrocks.

Previous studies have shown that the strength of the bimrocks is strongly correlated with VBP. However, it is almost impossible to separate blocks from the matrix in many situations. SONMEZ et al [12, 13], KAHRAMAN et al [14, 15], and SLATALLA et al [16] introduced digital image analysis to estimate VBP, but several inevitable uncertainty errors exist between 2D measurements and 3D values [17]. Despite these, ultrasonic non-destructive testing technology, which is an alternative method, was used to assess the mechanical properties of the bimrocks [18-20]. The effects of particle size distribution and VBP on ultrasonic wave velocity were systematically discussed. However, a stable ultrasonic signal could not be obtained when the block proportion exceeds 70%, due to the well-developed pore structure. By contrast, acoustic emission, which is a passive detection technique, provides a new process to evaluate the behaviour of the bimrocks such as fault breccia. SLATALLA et al [16] found that the complex behaviour of fault breccia under deformation can be described by analyzing the corresponding acoustic emissions. However, this approach is not preferred due to its complicated testing process.

With the deepening study, scholars found that it is difficult to predict the mechanical behaviors of the bimrocks based on a single parameter due to their complex components. Multi-regression model, therefore, has been widely used to improve the accuracy of prediction results [1, 21]. In recent years, the artificial neural network (ANN), which is a popular soft computing technique in geotechnical engineering [22-24], has been employed to estimate the mechanical properties of the bimrocks. Among these ANN technologies, back-propagation artificial neural network (BP-ANN) has been used to develop prediction models [25, 26]. To assure the accuracy of predicting results, proper network architectures of BP-ANN must be systematically designed to avoid over-learning. In addition, several computing parameters, such as the maximum number of training cycles and leaning rates, should be verified to improve the prediction capacity and computational efficiency.

On the basis of the literature review, no research has linked the vibration attenuation signals of the bimrocks to their mechanical properties. Traditional non-destructive testing methods, such as ultrasonic non-destructive testing technology, may not be able to obtain ideal testing results under the condition characterized by a high rock block proportion (RBP). Note that, the block proportion of the bimrocks used for non-destructive testing in most cases ranges from 25% to 70%. In nature, several kinds of geological formations exist with higher RBP and low matrix content such as cemented talus, mine waste dumps and cemented rockfill in underground mining [27-29]; their physical and mechanical characteristics are relatively different owing to the high block proportion. However, limited literature has reported the mechanical properties of the bimrocks with high block proportions [30, 31]. In addition, the existing prediction models [12, 14, 15] for mechanical properties of the bimrocks do not consider the data obtained from either artificial models or in-situ tests for the bimrocks with high RBP.

In the present study, the vibration attenuation signals of the artificial bimrocks with varying high rock block contents are investigated and analyzed, and the dynamic elastic modulus is obtained in accordance. Matrix strength that can indirectly reflect the boundary strength between the block and the matrix is also evaluated. In addition, the density of the bimrocks, which serves as a basic physical parameter for the bimrocks, is assessed. Then, the relationships between the three abovementioned parameters and the mechanical properties of the bimrocks are established on the basis of the results of uniaxial compressive test. Apart from the traditional statistical tools, such as simple and multiple regression analyses, an optimized general regression neural network (GRNN) algorithm, which is a more convenient and efficient computing technique relative to BP-ANN, is presented to develop a prediction model for the UCS and elastic modulus of the bimrocks.

2 Materials and testing method

The mechanical characteristics of the bimrocks are influenced by the roundness, distribution, size, and proportion of rock blocks. Among these impact factors, the proportion of rock blocks and the matrix strength play the most significant role in the mechanical behaviour of the bimrocks. With consideration of these critical factors, 64 cylindrical specimens with varying rock contents and matrix strength levels were fabricated to establish the relationships between the three aforementioned indicators and mechanical properties. The experimental setting groups are shown in Table 1, with four specimens scheduled to be evaluated for each setting group. Each specimen was a cylinder with a diameter of 100 mm and a height of 200 mm.

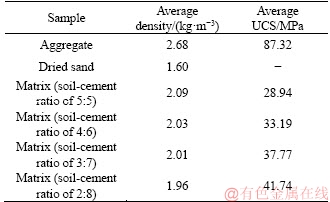
Table 1 shows the matrix composed of sand and cement with different mass ratios that is used to obtain specimens with varying matrix strength levels (with the same water cement ratio, 0.4). P.O.42.5 cement and sand were used to fabricate the mortar, as shown in Figure 1. The sand was dried and screened by using a 0.6 mm sieve to improve the homogeneity and fluidity of the mortar, and to make the mixture fill the iron moulds easily. As indicated by MEDLEY et al [6], the strength ratio between the matrix and the rock block of bimrocks should be greater than 2, which was satisfied in the present study by turning limestone into aggregates. As shown in Figure 1, the average uniaxial compressive strength of the rock cylinders (500 mm×100 mm) cored from the limestone was approximately 87 MPa, which was much higher than that of the matrix. The limestone used to obtain aggregates had good integrality with no obvious fissure structure to guarantee the strength of the particles. As shown in Table 1, the particle size of the rock block is unified with the same gradation, ranging from 4.5 to 20 mm (based on testing technical standards [32, 33]). The relevant mechanical parameters of the rock blocks, sand and matrix are shown in Table 4.

Table 1 Specimen combination

Figure 1 Aggregate size distribution of rock particles prepared for artificial bimrocks:

During the specimen preparation, dried sand, cement and rock blocks were poured in a mixing machine sequentially and were stirred for 30 s. Then, water was moderately added and was stirred well. The inner wall of the mould was consistently coated with mineral oil. The mixtures were placed in three approximately equal layers, and each layer was subjected to mechanical vibration for 20 s. The specimens were demoulded after 24 h. For curing, the specimens were kept in a moist environment at a temperature of approximately 25 °C and relative humidity of 95% for 7 d. Before the tests, each cylinder specimens was capped at both ends with a gypsum capping compound to ensure that the two ends were planar.

An E-Meter MK Ⅱ resonance frequency tester with an accelerometer sensitivity of 9.60 mV/g was adopted (Figure 2(a)) to capture the vibration response characteristics of the bimrock specimen. The servo-hydraulic testing machine used to perform the uniaxial compressive tests is shown in Figure 2(b). During the loading process, the loading rate was controlled at 0.3 MPa/s for all specimens [34]. In each test, the loading was terminated when the measured stress drops to 10% of the peak strength. In addition, density test was conducted on the specimens.

3 Laboratory test results

3.1 Analysis of resonance test results

Figure 3 shows the primitive test results of vibration acceleration for the specimens containing 65% and 80% block proportions. As shown, the vibration signals of bimrocks were well received, especially under a high RBP.

Figure 2 Test equipments (a) and prepared bimrocks with different RBPs(b)

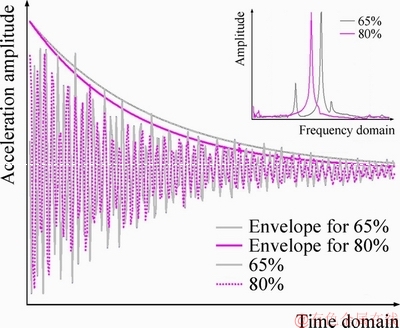
Figure 3 Primitive test result of vibration acceleration

The bimrocks with high block proportion consist of various components with widely contrasting physical properties, such as matrix, rock blocks and pores. With the increasing block proportion, the voids of specimens raise up, which lead to the increase of vibration damping. Thus, the attenuation of vibration acceleration of the bimrocks with a higher block proportion (80%) is more apparent compared to cases with 65% rock content (Figure 3). However, the difference was relatively small, and could be influenced by the quality of signal acquisition.

By contrast, the acceleration resonance frequencies of the specimens with varying block proportions exhibit distinct differences, as shown in Figure 3. The resonance frequency of the bimrocks decreases with the increase of the block proportion. In addition, stable test results are obtained despite the poor test signals. Hence, the vibration test is a suitable approach to investigate the physical and mechanical properties of the bimrocks. On the basis of the operator’s manual [35], the acceleration resonance frequency is automatically converted into dynamic elastic modulus by:

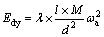                         (1)

where E_dy is the dynamic elastic modulus; ω_a is the acceleration resonance frequency; l is the height of the specimen; d is the diameter of the specimen; M is the mass of the specimen; and λ is the system constant, which is calibrated to 5.093 for a cylinder specimen and 4.000 for a prism specimen [35].

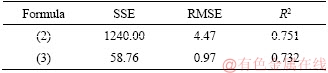
Then, the correlations between dynamic elastic modulus and mechanical properties are established on the basis of the experiment results of uniaxial compressive test. Simple regression analyses are performed with the least squares method to understand the relations between dynamic elastic modulus and mechanical properties. As shown in Table 2, strong correlations are observed between dynamic elastic modulus and mechanical properties, such as UCS and elastic modulus. The fitting curve is shown in Figure 4. Thus, the equations of these fitting lines can be expressed as:

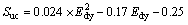              (2)

E=0.2339×E_dy-3.181                        (3)

where S_uc is the uniaxial compressive strength, and E is elastic modulus.

Table 2 Predictive performance indices of simple regression

A clear increasing trend of UCS is observed with the increase in the dynamic elastic modulus. A polynomial type relation is obtained between dynamic elastic modulus and UCS (Eq. (2)). In addition, a linear correlation is found between elastic modulus and dynamic elastic modulus. As shown in Figure 4(b), the elastic modulus grows linearly with the increase in dynamic elastic modulus, as described by Eq. (3). These results indicate that the mechanical properties of the bimrocks are successfully estimated on the basis of the test results for dynamic elastic modulus.

Figures 4(a) and (b) demonstrate a large decline in the mechanical properties with the increase of the block proportion, especially when the RBP increases from 65% to 70%. This finding is contrary to those in several previous studies [12, 18, 36], in which the RBP mainly ranges from 20% to 60%. In those cases, the mechanical properties are enhanced as the block proportion increases, owing to the contrasting mechanical properties of the rock blocks and matrix. However, the rock blocks tend to come into contact with one another when the block proportions get higher; this condition leads to remarkable increase in porosity.

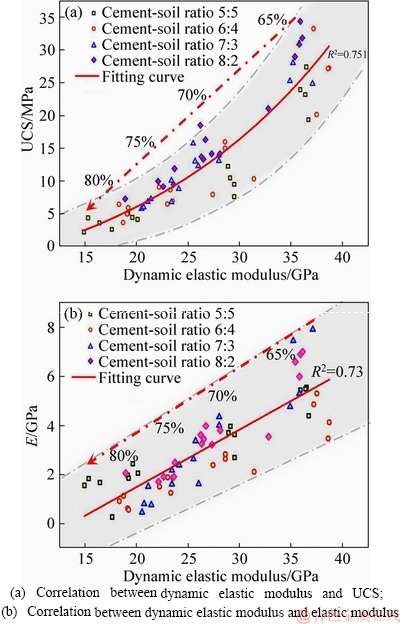
Figure 4 Correlations between dynamic elastic modulus and mechanical properties:

Therefore, the bearing mechanism of the bimrocks changes to a great extent, and corresponds to a lower USC and elastic modulus.

3.2 Analysis of density test results

A scatter diagram between the densities and block proportions of all the specimens is presented in Figure 5. A clear reduction trend of density is observed with the increase of block proportion. As mentioned in Section 3.1, the remaining matrix of the bimrocks could not fill the gaps among the rock blocks with the increasing content of rock blocks. This condition leads to a remarkable increase in the porosity of the bimrocks. Consequently, the high porosity value is correlated to the low density and compactness of the bimrocks.

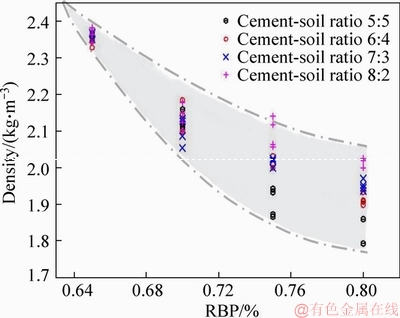
Figure 5 Density against varying block proportion

The mechanical properties show a consistent increasing trend with the increase of density. Polynomial and linear type relations are obtained between density and UCS and between density and elastic modulus. The equations of these fitting lines are expressed in Eqs. (4) and (5), respectively.

S_cu=26.63D²-64.54lD+30.69                (4)

E=9.628D-17.17                         (5)

where D is the density of the bimrocks.

Based on the regression performance indices of Table 3, density has a huge impact on the mechanical behavior of the bimrocks; and it can serve as a basic physical parameter to evaluate the porosity and mechanical properties of the bimrocks with high block proportions.

Similar to the dynamic elastic modulus and mechanical properties, density also undergoes remarkable change when the RBP increases from 65% to 70%, as shown in Figure 6. This finding indicates that the pore size and scale of the bimrocks with 70% rock blocks differ from those with 65% rock. This difference explains the sharp reduction in the strength and density of the bimrocks. Therefore, based on the obvious distinction of the physical and mechanical properties, the composite samples fall in the scope of high rock block proportions when the rock proportion reaches 70%; this outcome is consistent with the definition in Refs. [25, 26].

Table 3 Predictive performance indices of simple regression

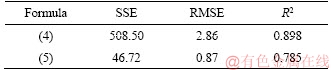
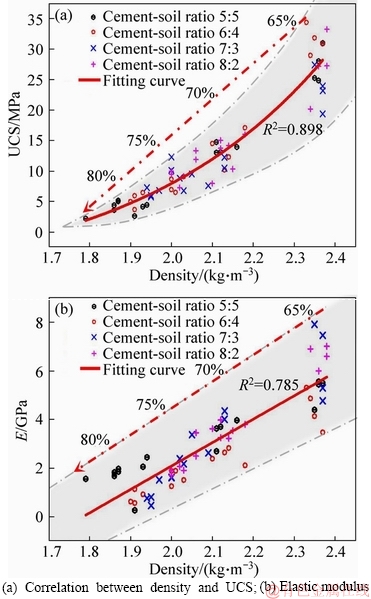
Figure 6 Correlations between density and mechanical properties:

3.3 Effects of matrix strength on mechanical properties of bimrocks

The interface between the matrix and rock blocks is considered the weakest portion of the bimrocks that is strongly influenced by the matrix strength. In Figure 7, failure morphology is represented by red solid lines. The split of the interfaces between the matrix and rock blocks is the common failure pattern in the most bimrocks, especially when the rock block content exceeds 70%. In addition, split failure occurs in the matrix when the block proportion is 65%. Hence, matrix strength plays an important role in the estimation of mechanical properties.

Figure 7 Failure morphology for bimrocks under uniaxial compressive test

As shown in Figure 8, the dynamic elastic modulus of the bimrocks with the same block proportions linearly increases with the increase of cement ratio, because a high cement ratio corresponds to a high strength and cementation capability of the matrix (Figure 9(b)). These features can effectively unify the composite sample as a whole and improve its strength. Therefore, the dynamic elastic modulus of the bimrocks is sensitive to the changes in the matrix properties of the bimrocks with the same block proportion.

The influences of matrix strength on the mechanical properties of the bimrocks are further analyzed through uniaxial compressive tests. As shown in Figure 9 and Table 4, the UCS of the bimrocks is significantly affected by the matrix strength. In particular, the bimrocks with varying block proportion share a consistent increasing trend in their UCS with the increase of the cement ratio. Thus, matrix strength should be taken into account in predicting the mechanical properties of the bimrocks.

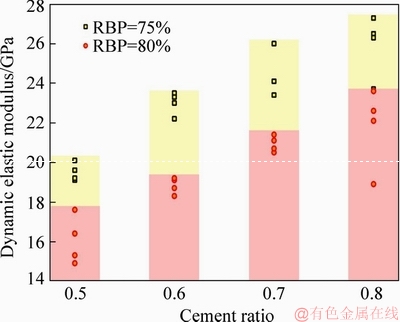
Figure 8 Dynamic elastic strength with varying cement ratios

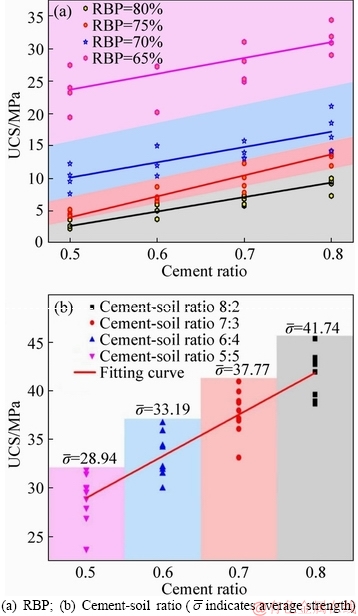
Figure 9 Effects of matrix strength on mechanical properties of bimrocks:

Table 4 Properties of rock block and matrix

4 Multivariable prediction models

4.1 Multi-regression model

As previously discussed, the mechanical properties of the bimrocks have a strong correlation with dynamic elastic modulus, density and matrix strength. However, prediction models based on simple regression cannot simultaneously reflect the influences of different factors. Hence, the accuracy of the simple regression is usually limited. To improve the predictive performance, multi- regression analysis is adopted to establish a comprehensive prediction model. Dynamic elastic modulus, density, and matrix strength are all considered in the multi-regression model. A polynomial relation is used in UCS prediction. For the sake of simplicity, a linear type relation is adopted to predict the elastic modulus.

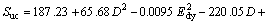
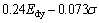                      (6)

E=-12.24+8.24D+0.074E_dy-0.11σ           (7)

where σ is the matrix strength.

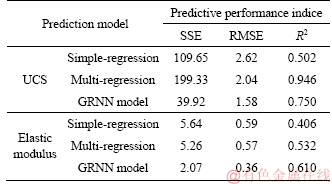
The relationships between the mechanical properties and three input parameters are obtained by using the least squares method, as shown in Eqs. (6) and (7). The predictive performance indices are listed in Table 5. The curves with 45° line (y=x) were extracted to compare the validity degree between the simple regression and multi- regression models [37-40], as shown in Figure 10. The multi-regression model provided a satisfactory solution to predict the mechanical properties of the bimrocks. It also proves from another perspective that the aforementioned physical and mechanical parameters are crucial indicators that play pivotal roles in the prediction process.

Table 5 Prediction performance indices of simple regression and multi-regression

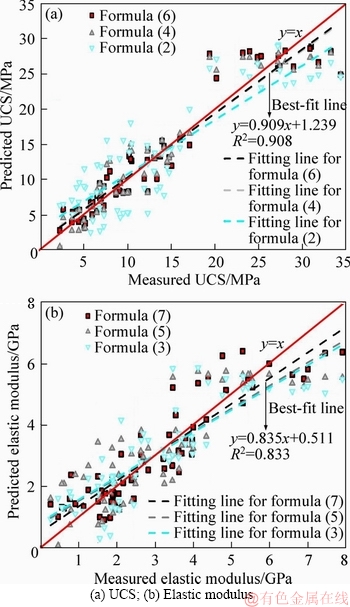
Figure 10 Comparisons of multi-regression model and simple regression model:

4.2 Prediction model based on GRNN algorithm

With the development of intelligent algorithms, such as ANN, soft computing techniques have been increasingly applied to solve engineering problems especially in geology. Recently, the BP-ANN has been used to construct prediction models in geo- engineering applications [26]. However, an appropriate network architecture should be systematically designed in the hidden layer to achieve good predictive performance. To avoid overlearning, system parameters, such as the maximum number of training cycles, should be properly selected according to the characteristics of the input data and network structure. In sum, various experiments and comparisons should be conducted until an ideal prediction model based on BP-ANN is obtained.

The GRNN proposed by SPECHT [41] is characterized by a simple and clean network architecture and fast training speed. It performs Parzen nonparametric estimation and the maximum probability principle. GRNN can acquire a relatively acceptable prediction result with limited input data. The ultimate formula for the predicted output is obtained by:

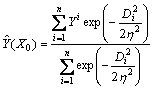                   (8)

where 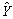is the predicted output vector; X₀ is the input vector for prediction; η is the smooth factor; n is the number of training samples; Yⁱ is the output vector used for training and 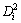is the Euclidean distance obtained by:

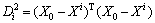                   (9)

where Xⁱ is the input vector used for training.

The network architecture of GRNN consists of four layers, namely, input, hidden, summation and output layers, as shown in Figure 11. The neurons of the input layer receive the input vector, and the number of neurons in this layer is equal to the dimension of the input vector. The information of the input layers is transferred to the hidden layer by using a linear function. The hidden layer is the radial basis layer, whose number of neurons is equal to the number of training samples. A Gauss function is generally used as the activation function in the hidden layer, in which the central vector of the ith neuron is the input vector Xⁱ of the ith training sample. In the summation layer, neurons are divided into denominator and numerator units, which compute the algebraic and weighted sums of the hidden unit outputs, respectively. Weight vector Y of the numerator unit denotes the expected outputs of the training samples. The predictive value of GRNN can be obtained by dividing the output of the numerator unit with the output of the denominator unit in the summation layer.

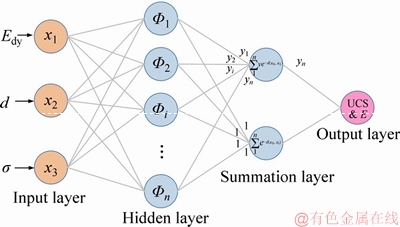
Figure 11 Technical process of GRNN algorithm

As shown in the calculation process of GRNN, the network architecture is determined when the input layer receives the training samples. In the GRNN algorithm, the weights and biases between the network layers do not require repeated training and adjustment similar to the BP-ANN algorithm. Consequently, the computation efficiency is remarkably improved. However, the performance of the GRNN algorithm is strongly influenced by smooth factor η. The smooth factor should be optimized to obtain an ideal network. In this study, a genetic algorithm is adopted to optimize the smooth factor. The variance sum between the prediction results and the training data is set as the objective function. Figure 12 displays the technical procedure for determining the mechanical properties of the bimrocks on the basis of the optimized GRNN model.

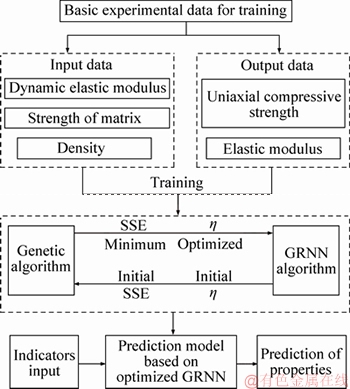
Figure 12 Technical procedure for determining mechanical properties of bimrocks (SSE is variance sum and η is smooth factor)

The optimized GRNN trained with 64 sets of input data shows yields good prediction results, which are approximately the same as the primitive experiment data. Hence, the trained network can precisely reflect the nonlinear relation between the input data and the output data with the optimized smooth factor. Another experiment was conducted to investigate the predictive performance of the optimized GRNN algorithm.

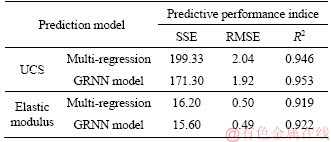
As each group comprises four sets of experiment data, another 64 sets of data could be fabricated by taking the mean of the three sets of data of each group. The fabricated data maintain most of the characteristic of the raw data and are used to validate the performance of the prediction model. The prediction results are presented in Figure 13 and Table 6. Relative to the results in Section 4.1, the predictive performance of the multi-regression model is improved due to fabrication data. Nevertheless, the prediction results of the optimized GRNN remain close to the testing data. As shown in the distribution form of the prediction results in Figure 13, the GRNN prediction model effectively reflected the nonlinearity and randomness between the three indicators and the mechanical properties of the bimrocks with high rock proportions.

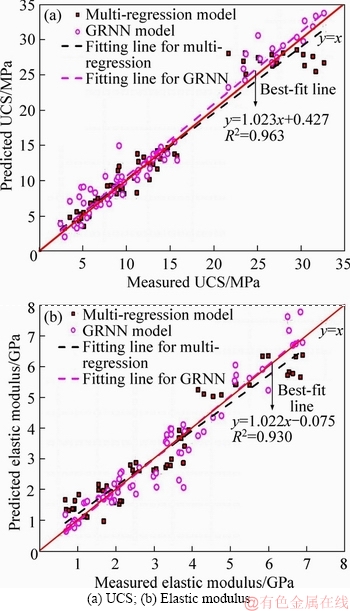
Figure 13 Comparison between multi regression and GRNN model:

Table 6 Predictive performance indices of multi- regression and optimized GRNN

5 Discussion and validation

The performance of the optimized GRNN model is further discussed on the basis of the valuable experimental data on volcanic bimrocks from the work of SONMEZ et al [26], in which the block proportion, number of rock fragments and line fractal dimensions were used as the basic data to predict the values of UCS and elastic modulus. For the volcanic bimrocks, the rock fragments show a better correlation with the mechanical properties in comparison with the line fractal dimensions and block proportion. Therefore, parts of regression based prediction models are listed as follows:

S_uc=-7.388lnB+42.967                     (10)

E=-0.966lnB+5.9943                       (11)

S_uc=-4.833lnP_c+25.259                     (12)

E=-0.64lnP_c+3.6886                       (13)

P_c=B×(1-P_vb/100)/(100×(D_i-1))              (14)

where B is the rock fragments, P_vb is the volume block proportion, D_i is the line fractal dimensions and P_c is the combined parameter.

The trained network of optimized GRNN was obtained through the basic data from Ref. [26]. Then, the predicted and measured results for the three models are compared (Figure 14). As shown in Table 7, although the higher predictive performance is obtained from the multi-regression model compared with the simple regression model, the optimized GRNN model still shows better prediction results for UCS and elastic modulus. In addition, the input and output data of the volcanic bimrocks used for training have greater divergence than the experimental data obtained in this study. Therefore, the optimised GRNN presents good adaptability in this case.

6 Conclusions

In this study, a series of laboratory experiments, including resonance frequency, uniaxial compressive and density tests, is conducted to investigate the mechanical properties of the bimrocks with high RBPs. The dynamic elastic modulus obtained from the resonance frequency test shows a strong correlation with the UCS and elastic modulus. It could thus serve as a practical index for determining mechanical properties. In addition, the dynamic elastic modulus is found to be a function of both block proportion and matrix strength.

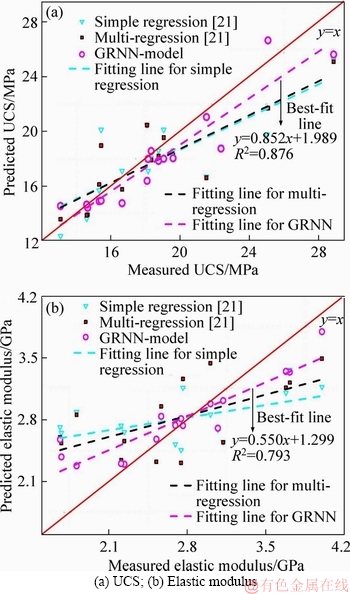
Figure 14 Validation results of GRNN models:

Table 7 Comparisons of predictive performance indices

The density of the bimrocks can also be used to estimate mechanical properties, because the relations between mechanical properties and density are strong and statistically relevant. In addition, mechanical properties are enhanced with the increase of matrix strength. Therefore, matrix strength should be considered during prediction.

Compared with simple regression model, the multi-regression model shows an improved predictive performance because of its consideration of various influencing factors. Despite that, the proposed optimized GRNN model can provide better prediction results than the multi-regression model. The validity and applicability of the proposed optimized GRNN model are verified on the basis of the comparison between the predicted and measured mechanical properties, using the fabricated data in this work and available data in previous study. The results demonstrate that the optimized GRNN model can be used as an alternative tool for the estimation of the mechanical properties of the bimrocks.

References

[1] SONMEZ H, GOKCEOGLU C, MEDLEY E W, TUNCAY E, NEFESLIOGLU H A. Estimating the uniaxial compressive strength of a volcanic bimrock[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(4): 554-561. DOI: 10.1016/ j.ijrmms.2005.09.014.

[2] MAHDEVARI S, MAAREFVAND P. Applying ultrasonic waves to evaluate the volumetric block proportion of bimrocks [J]. Arabian Journal of Geosciences, 2017, 10(9): 204. DOI: 10.1007/s12517-017-2999-8.

[3] KALENDER A, SONMEZ H, MEDLEY E, TUNUSLUOGLU C, KASAPOGLU K E. An approach to predicting the overall strengths of unwelded bimrocks and bimsoils [J]. Engineering Geology, 2014, 183: 65-79. DOI: 10.1016/j.enggeo.2014.10.007.

[4] ZHAO M H, LIU J J, LUO H, YANG Ming-hui. Experimental studies of shear strength characteristics and influencing factors of soil-rock aggregate mixture [J]. Yantu Lixue/Rock and Soil Mechanics, 2017, 38(4): 965-972. DOI:10.16285/j.rsm. 2017. 04.006.

[5] ZHANG Hai-yang, XU Wen-jie, YU Yu-zhen. Triaxial tests of soil–rock mixtures with different rock block distributions [J]. Soils & Foundations, 2016, 56(1): 44-56. DOI: 10.1016/ j.sandf.2016. 01.004.

[6] MEDLEY E, GOODMAN R E. Estimating the block volumetric proportions of melanges and similar block- in-matrix rocks (bimrocks) [C]// 1st North American Rock Mechanics Symposium. Austin, the United States, 1994: 1-8.

[7] LINDQUIST E S. The strength and deformation properties of melange [D]. Department of Civil Engineering, University of California, 1994. https://ci.nii.ac.jp/naid/ 10006538153.

[8] NIE Zhi-hong, LIANG Zheng-yu, WANG Xiang, GONG Jian. Evaluation of granular particle roundness using digital image processing and computational geometry [J]. Construction and Building Materials, 2018, 172: 319-329. DOI:10.1016/j.conbuildmat. 2018.03.246.

[9] WANG Xiang, LIANG Zheng-yu, NIE Zhi-hong, GONG Jian. Stochastic numerical model of stone-based materials with realistic stone-inclusion features [J]. Construction and Building Materials, 2019, 197: 830-848. DOI:10.1016/j.conbuildmat.2018.10.062.

[10] MAHDEVARI S, MOAREFVAND P. Experimental investigation of fractal dimension effect on deformation modulus of an artificial bimrock [J]. Bulletin of Engineering Geology and the Environment, 2017, 77(4): 1729-1737. DOI: 10.1007/s10064-017-1074-8

[11] XU Wen-jie, YUE Zhong-qi, HU Rui-lin. Study on the mesostructure and mesomechanical characteristics of the soil–rock mixture using digital image processing based finite element method [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(5): 749-762. DOI: 10.1016/j.ijrmms. 2007.09.003.

[12] SONMEZ H, ERCANOGLU M, KALENDER A, DAGDELENLER G, TUNUSLUOGLU C. Predicting uniaxial compressive strength and deformation modulus of volcanic bimrock considering engineering dimension [J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 86: 91-103. DOI: 10.1016/j.ijmms. 2016.03.022.

[13] SONMEZ H, GOKCEOGLU C, TUNCAY E, MEDLEY E W, NEFESLIOGLU H A. Relationship between volumetric block proportion and overall UCS of a volcanic bimrock [J]. Felsbau: Rock Soil Engineering, 2004, 22(5): 27-34. https://www.researchgate.net/publication/265277014.

[14] KAHRAMAN S, ALBER M. Estimating unconfined compressive strength and elastic modulus of a fault breccia mixture of weak blocks and strong matrix [J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(8): 1277-1287. DOI: 10.1016/j.ijrmms.2006.03.017.

[15] KAHRAMAN S, ALBER M, FENER M, GUNAYDIN O. Evaluating the geomechanical properties of Misis fault breccia (Turkey) [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(8): 1469-1479. DOI: 10.1016/j.ijrmms. 2008.02. 010.

[16] SLATALLA N, ALBER M, KAHRAMAN S. Analyses of acoustic emission response of a fault breccia in uniaxial deformation [J]. Bulletin of Engineering Geology & the Environment, 2010, 69(3): 455-463. DOI: 10.1007/s10064 -010-0296-9.

[17] HANEBERG W C. Simulation of 3-D block populations to characterize outcrop sampling bias in block-in-matrix rocks(bimrocks) [J]. Felsbau: Rock Soil Engineering, 2004, 22(5): 19-26. http: //bimrocks.com/ bimsite/ wp-content/ uploads/2010/07/HanebergFelsbau2004.pdf.

[18] KAHRAMAN S, ALBER M, FENER M, GUNAYDIN O. An assessment on the indirect determination of the volumetric block proportion of Misis fault breccia (Adana, Turkey) [J]. Bulletin of Engineering Geology & the Environment, 2015, 74(3): 899-907. DOI: 10.1007/s10064- 014-0666-9.

[19] WANG Yu, LI Xiao. Experimental study on cracking damage characteristics of a soil and rock mixture by UPV testing [J]. Bulletin of Engineering Geology & the Environment, 2015, 74(3): 775-788. DOI: 10.1007/s10064-014-0673-x.

[20] WANG Yu, LI Xiao, HU R L, LI Shou-ding, WANG J Y. Experimental study of the ultrasonic and mechanical properties of SRM under compressive loading [J]. Environmental Earth Sciences, 2015, 74(6): 5023-5037. DOI:10.1007/s12665-015-4529-x.

[21] SONMEZ H, TUNCAY E, GOKCEOGLU C. Models to predict the uniaxial compressive strength and the modulus of elasticity for Ankara Agglomerate [J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(5): 717-729. DOI: 10.1016/j.ijrmms.2004.01.011.

[22] YESILNACAR E, TOPAL T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey) [J]. Engineering Geology, 2005, 79(3): 251-266. DOI: 10.1016/j.enggeo.2005.02.002.

[23] AKSOY H, ERCANOGLU M. Determination of the rockfall source in an urban settlement area by using a rule-based fuzzy evaluation [J]. Natural Hazards and Earth System Sciences, 2006, 6(6): 941-954. DOI: 10.5194/nhess-6-941- 2006.

[24] SONMEZ H, GOKCEOGLU C, KAYABASI A, NEFESLIOGLU H A. Estimation of rock modulus: For intact rocks with an artificial neural network and for rock masses with a new empirical equation [J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(2): 224-235. DOI: 10.1016/j.ijrmms. 2005.06.007.

[25] KAHRAMAN S, GUNAYDIN O, ALBER M, FENER M. Evaluating the strength and deformability properties of Misis fault breccia using artificial neural networks [J]. Expert Systems with Applications, 2009, 36(3): 6874-6878. DOI: 10.1016/j.eswa. 2008.08.002.

[26] SONMEZ H, ERCANOGLU M, KALENDER A, DAGDELENLER G, TUNUSLUOGLU C. Predicting uniaxial compressive strength and deformation modulus of volcanic bimrock considering engineering dimension [J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 86: 91-103. DOI: 10.1016/ j.ijmms.2016.03.022.

[27] GUO Wei-yao, ZHAO Tong-bin, TAN Yun-liang, YU Feng-hai, HU Shan-chao, YANG Fu-qiang. Progressive mitigation method of rock bursts under complicated geological conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 96: 11-22. DOI: 10.1016/j.ijrmms. 2017.04.011.

[28] GUO Wei-yao, TAN Yun-liang, YU Feng-hai, ZHAO Tong-bin, HU Shan-chao, HUANG Dong-mei, QIN Zhe. Mechanical behavior of rock-coal-rock specimens with different coal thicknesses [J]. Geomechanics and Engineering, 2018, 15(4): 1017-1027. DOI: 10.12989/gae. 2018.15.4.1017.

[29] ZHAO Tong-bin, GUO Wei-yao, TAN Yun-liang, LU Cai-ping, WANG Cheng-wu. Case histories of rock bursts under complicated geological conditions [J]. Bulletin of Engineering Geology and the Environment, 2018, 77(4): 1529-1545. DOI: 10.1007/s10064-017-1014-7.

[30] AFIFIPOUR M, MOAREFVAND P. Mechanical behavior of bimrocks having high rock block proportion [J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 65(1): 40-48. DOI: 10.1016/j.ijrmms.2013.11.008.

[31] AFIFIPOUR M, MOAREFVAND P. Experimental study of post-peak behavior of bimrocks with high rock block proportions [J]. Journal of Central South University, 2014, 21(2): 761-767. DOI: 10.1007/s11771-014-1999-z.

[32] Nanjing Water Conservancy Science Research Institute. Soil test technical manuals [M]. Beijing: China Communication Press, 2004. (in Chinese)

[33] BS1377-1. Methods of test for soils for civil engineering purposes—Part 1: General requirements and sample preparation [S].

[34] GB/T 50266-2013. Standards for test methods of engineering rock mass [S].

[35] Operator’s manual for E-Meter MK II resonance frequency tester [M]. Chicago: James Instruments Inc, 2013.

[36] YANG Hao, ZHOU Zhong, WANG Xiang-can, ZHANG Qi-fang. Elastic modulus calculation model of a soil-rock mixture at normal or freezing temperature based on micromechanics approach [J]. Advances in Materials Science and Engineering, 2015, 576080: 1-10. DOI: 10.1155/2015/576080.

[37] FEREIDOONI D. Determination of the geotechnical characteristics of hornfelsic rocks with a particular emphasis on the correlation between physical and mechanical properties [J]. Rock Mechanics & Rock Engineering, 2016, 49(7): 1-14. DOI: 10.1007/s00603-016-0930-3.

[38] KHAJEVAND R, FEREIDOONI D. Assessing the empirical correlations between engineering properties and P-wave velocity of some sedimentary rock samples from Damghan, northern Iran [J]. Arabian Journal of Geosciences, 2018, 11(18): 528-547. DOI: 10.1007/s12517-018-3810-1.

[39] LIN Yue-xiang, PENG Li-min, LEI Ming-feng, WANG Xiang, CAO Cheng-yong. Predicting the mechanical properties of bimrocks with high rock block proportions based on resonance testing technology and damage theory [J]. Applied Sciences, 2019, 3537: 1-15. DOI: 10.3390/ app9173537.

[40] LEI Ming-feng, LIU Ji-yao, LIN Yue-xiang, SHI Cheng-hua, LIU Can. Deformation characteristics and influence factors of a shallow tunnel excavated in soft clay with high plasticity [J]. Advances in Civil Engineering, 2019, 7483628: 1-14. DOI: 10.1155/2019/7483628.

[41] SPECHT D F. A general regression neural network [J]. IEEE Transactions on Neural Networks, 2002, 2(6): 568-576. DOI: 10.1109/72.97934.

(Edited by FANG Jing-hua)

中文导读

高含石率胶结型土石混合体力学性能试验研究

摘要：本文基于单轴压缩以及共振频率试验，对多组不同特征的高含石率胶结型土石混合体试件进行测试，以探究其物理力学特性。试验结果显示，试件的动弹性模量与其单轴抗压强度、弹性模量以及含石率均存在显著的相关性。此外，试件的密度以及基质强度也与其宏观力学性能密切相关。因此，选取以上三项典型指标，对高含石率胶结型土石混合体的力学性能进行预测。除传统的回归分析手段以外，本文通过遗传算法对广义回归神经网络算法进行优化，并建立了相应的预测模型。预测结果表明，尽管多元回归分析相对于一元回归分析而言预测性能有所提高，但基于优化回归神经网络的预测结果更为理想。分别采用试验数据以及文献中的数据，证实了所建立的预测模型具有良好的适应性和理想的预测性能。

关键词：胶结型土石混合体；高含石率；共振频率测试；广义回归神经网络

Foundation item: Projects(51978669, U1734208) supported by the National Natural Science Foundation of China; Project(2018JJ3657) supported by Natural Science Foundation of Hunan Province, China

Received date: 2018-10-22; Accepted date: 2019-01-22

Corresponding author: LEI Ming-feng, PhD, Associate Professor; Tel: +86-13787232438; E-mail: mingdfenglei@csu.edu.cn; ORCID: 0000-0001-7416-7709