并行组合扩频系统误比特率公式的改进及主要参数的优化

郭黎利¹，刘明夺¹，姜晓斐²，孙志国¹

(1. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001；

2. 中国电子科技集团第54研究所 微波散射部，河北 石家庄，050001)

摘要：分析并行组合扩频系统的运行原理，改进原有误比特率公式。为实现并行组合扩频系统主要参数的优化选取，结合系统误比特率公式分析主要参数对误码性能的影响。最后，综合研究结果给出并行组合扩频系统主要参数的选取原则。研究结果表明：在相同信噪比条件下，当正交扩频序列总数固定时，系统误码性能随着每次选取发射的正交扩频序列数的增加而迅速降低；而当每次选取发射的正交扩频序列数固定时，系统的平均误比特率随正交扩频序列总数增加而阶梯状下降，但系统的复杂度随之增加而呈线性增加。

关键词：并行组合扩频通信系统；误比特率公式；参数优化

中图分类号：TN914.2          文献标志码：A         文章编号：1672-7207(2013)05-1895-07

Improvement of bit error rate formula and optimization of main parameters in parallel combinatory spread spectrum system

GUO Lili¹, LIU Mingduo¹, JIANG Xiaofei², SUN Zhiguo¹

(1. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China;

2. Microwave Scattering Department, The 54th Institute of China Electronic Technology Group Corporation,Shijiazhuang 050001, China)

Abstract: The operation principle of parallel combinatory spread spectrum (PCSS) system was analyzed, and the new bit error rate (BER) formula improved from original formula was derived. In order to optimize the main parameters of PCSS system, the influence of BER performance caused by the main parameters was mainly investigated combining the BER formulary. Finally, the selection principle of the main parameters was indicated in PCSS system. The research results show that under the same condition of signal-to-noise ratio, when the set number of pseudo-noise sequences is fixed, the BER performance decreases quickly while the number of selected pseudo-noise sequences increases. When the number of selected pseudo-noise sequences is fixed, the system performance (BER) decreases by stages when the set number of pseudo-noise sequences increase; however, the system complexity rises when the set number of pseudo-noise sequences increases linearly.

Key words: parallel combinatory spread spectrum system; bit error rate formula; parameters optimization

并行组合扩频(PCSS)系统是在直接扩频系统基础上发展而来的一种改进型的软扩频通信方式^[1]。相对于一般的直接扩频系统，该系统有更高的信息传输能力以及更高的频带利用率，从而得到国内外诸多学者的关注^[2-3]。朱近康^[4]提出并行组合扩频技术概念及其相关公式，为后续并行组合扩频系统的研究奠定了基础。但在系统仿真实验中，朱近康^[4]给出的并行组合扩频系统误比特率公式不能与仿真值完美贴合，存在一定的偏差。为此，本文作者在此公式基础上，更加细致地分析并行组合扩频系统性能，在原有误比特率公式上进行改进，得出更加准确的误比特率公式。改进后新公式的理论值和仿真值基本贴合，无偏差。此外，结合误比特率公式和仿真结果讨论并行组合扩频系统主要参数对误比特性能的影响，通过对参数的优化选择来改善系统性能。

1  并行组合扩频系统模型

并行组合扩频系统在发射端，每k比特数据d₁, d₂, …, d_k串并转换，然后送入数据-序列映射器。在M个伪随机序列样本集合P_{N, i}(i=1, 2, …, M)中，取出r个不同的伪随机序列样本，同时考虑伪随机序列的极性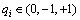, (i=1, 2, …, M)，形成组合序列；将该组合序列进行对应码片的等幅度叠加(+1或-1值相加)，形成多值实数序列：

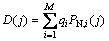             (1)

其中：q_i为伪随机序列选取控制因子；q_i=0表示不选取对应的序列P_N,i，且q_i=0的取值共有(M-r)个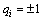；则表示选取序列P_N,i或序列P_N,i的互补形式。

基带并行组合扩频通信系统发射端结构如图1所示。由于并行组合扩频扩频通信系统中，共有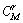个序列选择状态，同时选取的r个序列有2^r个极性状态，则每次发送的数据量k可确定为

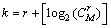             (2)

其中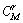：表示从M个不相同的元素中不重复的选r个的组合数；[x]表示对x取整数部分。

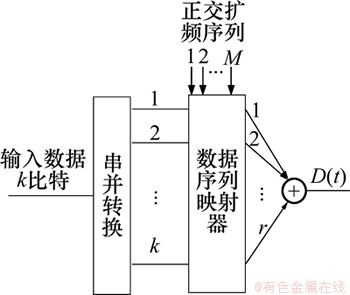
图1　基带并行组合扩频系统发射端框图

Fig.1　Transmitter of baseband PCSS

在并行组合扩频系统中，数据序列映射方式为依据从M个扩频序列中选取r个扩频序列的状态来映射(k-r)比特数据，进一步根据这r个扩频序列的极性完成r比特数据的映射，这样可实现总数为k比特数据的映射^[5-7]。

接收端在本地伪随机序列解扩之后，依据序列-数据逆映射算法，从M个扩频序列相关器输出值中选出绝对值最大的r个，并结合其极性即可解调出原始发射信息^[8-10]。基带并行组合扩频通信系统接收端结构如图2所示。

2  系统工作性能分析及比特误码率公式推导

通过并行组合扩频系统的接收方式可知，系统的最终误比特率性能主要受到接收端解扩相关器输出的模值以及其极性2部分的影响。其中：输出值的模值影响到r个发送序列组合的正确解调，即对应(k-r)比特数据的正确解调；而输出值的极性即为r个发送扩频序列的极性，则依次对应r比特数据。假定发送数据中“0”和“1”等概率出现，对k比特数据的差错概率分2步进行，具体步骤如下。

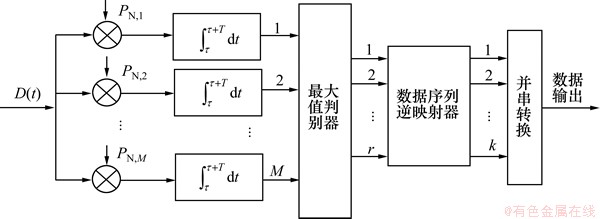
图2　基带并行组合扩频系统接收端框图

Fig.2　Receiver of baseband PCSS

步骤1 依据扩频序列相关器输出值的模值来确定(k-r)比特数据的平均错误比特数。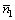

在信道中传输的多值序列在接收端送入解扩相关器，第j个相关器输出为

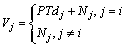               (3)

其中：j=1, 2, …, M ；j=i表示第j个解扩码和传输的多值信号相关，即解扩码为发送端所选择的r个扩频码P_N,i之一；j≠i表示第j个解扩码P_N,i和传输的多值信号不相关，即解扩码不是发送端所选的扩频码；d_j为系统解调出的数据信息的极性，；N_j为解扩后噪声。

从发送端来看，若发送端所选择的r个扩频码之一为第i个扩频序列，则在接收端，第i个相关器输出值V_i的绝对值比其余解扩相关器中的(M-r)个的输出值的绝对值都大，即|V_i|＞|V_m|(m=1, 2, …, M-r)，第i个解扩相关器的正确解调概率为^[11]

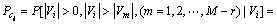
        (4)

则r个扩频序列总的解调误比特率为

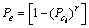                   (5)

而当解扩出错时，扩频序列对应的(k-r)比特数据中会出现n₁比特数据差错。出错比特数n₁的均值为

              (6)

因此，这(k-r)比特数据的平均错误比特数可由条件概率求得：

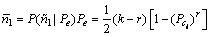     (7)

步骤2 依据扩频序列相关器输出值的极性来确定剩余r比特数据的平均错误比特数。

发送数据中“0”和“1”等概率出现，表示为b=0和b=1，且扩频序列极性与数据信息一一对应，则发送扩频序列的正负极性出现概率也相同。此时，发送扩频序列极性接收正确的平均概率等价于发送正极性扩频序列的极性正确接收概率，于是，有

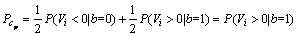            (8)

且极性正确接收概率等价于每比特数据的正确接收概率。因此，r比特数据中出现n₂比特数据差错，n₂的均值为

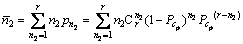      (9)

最后，结合上述2步所得结果，可求得系统最终的误比特率为

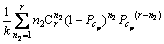        (10)

由于发送数据中“0”和“1”等概率出现，且扩频序列极性与数据信息一一对应，故发送扩频序列的正负极性出现概率也相同。不妨设发送的第i个扩频序列为正极性，且信道中噪声为0均值且双边功率谱密度为N₀/2的高斯白噪声，则V_i的概率密度为

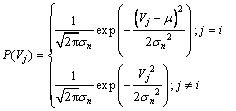        (11)

其中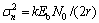：；，E_b为每bit信息数据能量。即V_i的概率密度服从均值为μ、方差为的高斯分布，V_m的概率密度服从均值为0、方差为的高斯分布。于是，可以将式(4)改写为

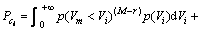
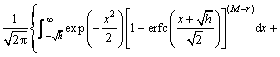
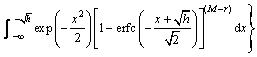 (12)

其中：，表示第i个扩频序列相关器的输入信噪比。

将式(11)代入式(8)，即可得到发送扩频序列极性接收正确的平均概率为

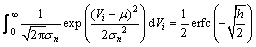 (13)

其中：erfc(·)是互补误差函数。由于极性解调出错概率远小于扩频解调差错概率^[12]；在此条件下可忽略极性解调出错概率，得到并行组合扩频系统的数据平均误比特率为

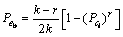             (14)

其中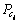：由式(12)给出。若信道为无多径高斯白噪声信道，则并行组合扩频系统的误比特率为

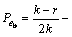
                   (15)

其中：h为系统扩频序列相关器输出端接收到的信噪比。

相对于原始并行组合扩频通信系统比特误码率公式，本文作者提出的改进公式是在原有公式的基础上加乘了系数，系数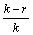表示传输信息中解扩时判定输出模值部分信息所占百分比，改进后系统误比特率公式更精准也更易解释。

3  并行组合扩频系统主要参数的优化

并行组合扩频系统在无多径高斯白噪声信道条件下的平均误比特率(式(15))可以看出：当h确定时，扩频序列总数M和选取的扩频序列数目r是主要影响系统抗噪声性能的2个参数。分析M和r对系统性能的影响有着重要意义。

在下面的分析中，并行组合扩频数据序列映射采用改进r-组合映射编码算法^[13-15]。正交扩频序列的类型对系统性能基本没有影响，为了不失一般性，采用周期为128的Walsh码；信源等概率出现且独立同分布，假定信道为无多径高斯白噪声信道，且系统已经同步。图3和图4中设定系统信噪比E_b/N₀=8 dB，改变并行组合扩频系统主要参数M和r，得到系统误码性能与上述参数之间的关系，分析其对系统的影响。

3.1  选取的扩频序列数r对系统性能影响

假设扩频序列集合中的序列总数M一定，当r较小时，每次发送的信息数据量k随r增加而迅速增加；当r达到一定值r₀时，k达到最大值，随后，系统每次发生的数据量k则逐渐下降。因此，r的取值只有为[2, r₀]之间的整数时才具有工程实际意义。同时，当r取值越大，则多值序列D(j)的取值越多，需要后续的系统多进制调制的进制数越大，使得系统实现困难，因此，r取值不能过大。

建立并行组合扩频系统仿真平台，分别分析M=13以及M=16时，选取发射的序列数r变化对系统性能的影响。M=13时，计算得r₀=8，即r在[2, 8]的范围内取整数。当r=2时，k_min=8 bit；r=8时，k_max=18 bit。若M=16，则r₀=11，k将从8 bit增加至23 bit。图3所示为M分别取值13和16时并行组合扩频系统的平均误比特率R随r变化的曲线。

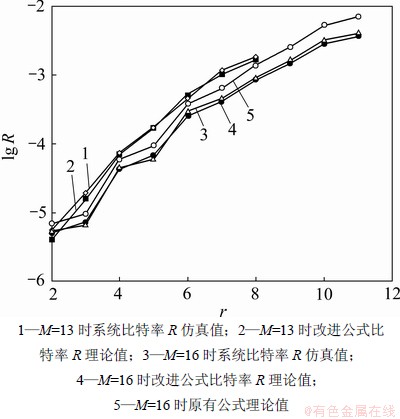
图3　不同M条件下选取发射的序列数r对并行组合扩频系统性能的影响

Fig.3　Impact of parameter r on PCSS system performance under different M

在图3可见：在M=13和M=16时的改进后误比特率R公式理论曲线和仿真曲线可以基本拟合，可见文中改进的公式的理论分析与搭建的仿真系统模型是一致的。且在M=16时使用原有误比特率公式计算的理论曲线明显略高于改进后公式计算的理论曲线，而系统的仿真曲线与改进后公式的理论曲线更接近，证明改进系统公式相对于原有系统公式计算更加准确。同时可以发现：无论M取何值，r越小，则系统的工作性能越好；当M=13时，随r的增大，k从8 bit增加至18 bit，系统的数据传输能力有了较大提高，频带利用率提高了1倍；然而，r与误比特率的对数约呈线性关系，系统的误比特率随r的增加迅速而增大；同样地，当M=16时，系统的误比特率随r的增加恶化，与误比特率的对数约呈线性关系。即系统可通过增加r来提高系统的频带利用率，但这是以降低系统的抗噪性能为代价的；这一点可以利用通信的有效性与可靠性之间的矛盾来解释。若假定系统的误比特率指标为10^-3，则当M=13时，以r≤6为宜；L=16时，以r≤7为宜。此时，将系统的误比特率控制在可接受的范围内，同时也可以大幅度地提高系统的数据传输能力。

3.2  扩频序列总数M对系统性能影响

为分析扩频序列总数M对并行组合扩频系统的影响，图4给出系统在r=4时，L在9到32范围内取值时系统误比特率随L变化的理论曲线与仿真曲线，其中的2条理论曲线分别由改进前原有系统平均比特误码率公式和改进后系统平均比特误码率公式计算得出。从图4可见：随着M的增大，系统的误比特率约呈阶梯状下降，即在某些M处，系统误比特率将出现跳变，且在下一次跳变之前基本保持平稳。图4中系统的仿真曲线与改进后公式的理论曲线更接近，证明改进系统公式的准确性，为并行组合扩频系统系统理论研究奠定了基础。

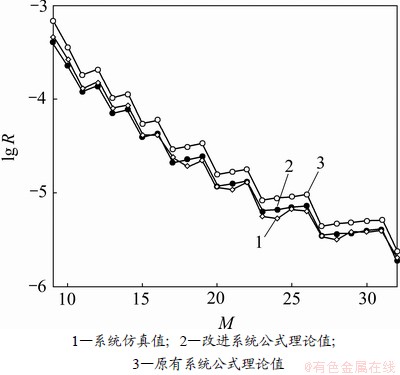
图4　正交扩频序列总数M对并行组合扩频系统性能的影响

Fig.4　Impact of parameter M on PCSS system performance

这种系统误比特率R随M增加而阶梯状下降的特性是由并行组合扩频系统自身特性决定的。由于k比特信息的总能量与r个扩频序列的总能量相等，故有kE_b=rE_PN(其中E_PN为每个扩频序列的总能量)。则每个扩频序列对应的信噪比h与系统信噪比E_b/N₀存在如下关系：

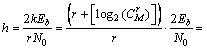
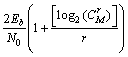                (16)

由式(16)可知：当r固定时，输出信噪比h随M的增大而增大，则系统误比特率整体趋势为随M增大而逐渐降低。由于运算中需对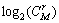进行取整运算，只有M增加到某一临界值使得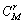的取值达到或超过2的整数次幂时，h才会增大。因此，h随M增加而成阶梯状增加，而系统误比特率将随M增大而呈阶梯状下降。

从图4可见：当M取值从9增加到32时，由于每个扩频序列对应的信噪比h也随之增加，系统的误比特率约降低3个数量级，系统的工作性能有较大改善。而且每次可发送的数据量k由10 bit增加至18 bit，约提升1倍，即系统的频带利用率约提升1倍；随着M的增大，并行组合扩频系统的有效性和可靠性同时有一定的提升。但是，应注意到：由于正交扩频序列总数M与系统的复杂度呈线性关系，系统的复杂度随M的增大也大幅上升；即这种系统性能的提升是以增加系统成本为代价的。因此，在设计系统时，M的取值不宜过大，否则系统成本过高，且不利于并行组合扩频系统的硬件实现。

在实际系统设计中，应根据系统实际要求，综合考虑r和M的取值。假定系统设计要求每次发送的数据量k=10 bit，当r=4时，M取8或9均满足条件；由于M=8为跳变点，因此，M应取值为8。同理，当r=3时，M应取值为11。这2组参数均可以满足系统要求。第1组参数的M取值小，故系统复杂度相对较低；第2组参数下系统的复杂度虽略有上升，但其系统误比特性能将优于第1组参数。两者的误比特率R随信噪比变化的曲线如图5所示。所以，应根据实际需求，选取第1组或者第2组参数；若对系统的复杂度无特殊要求，则取第2组参数r=3和M=11为宜。

因此，在实际系统设计中，应根据系统实际要求，以系统所需有效性为考虑基准，计算r和M的各种取值备选项，根据上述讨论的调制参数对系统性能影响的变化趋势来估算不同参数对系统可靠性和复杂度的影响，并结合系统复杂度来进行权衡，选取较小的M和r。

图5　不同参数下的并行组合扩频系统的性能曲线

Fig.5　BER performance of PCSS systems with two different sets of parameters

4  结论

(1) 对并行组合扩频通信系统进行理论研究，重点讨论系统的误码性能，在原有平均误比特率公式的基础上进行修正和改进，改进后的公式计算更加精确，仿真结果可以更好地与之匹配。

(2) 在误码率理论公式的基础上，研究并行组合扩频系统主要参数对系统性能的影响。通过结合仿真结果可知：并行组合扩频系统选取的扩频序列数r与系统误比特率的对数成线性关系，r增大时，误比特率也增大；而系统扩频序列总数M增大时，系统误比特率的对数呈阶梯下降趋势。从理论上详细分析了产生如上现象的原因，并以每次发送的数据量k=10 bit为例，分析并行组合扩频系统的主要参数优化选取的基本原则：根据系统设计的传输速率要求，综合考虑系统的误比特性能和复杂度，依此选取较小的M和r。

参考文献：

[1] ZHU Jinkang, GEN Marubayashi. Parallel combinatory SS communication[R]. Tokyo: IEICE Technical Report of Japan, 1990.

[2] 姜晓斐, 郭黎利, 齐琳, 等. 并行组合扩频超宽带系统的跳时多址接入方式[J]. 华南理工大学学报: 自然科学版, 2011, 39(9).

JIANG Xiaofei, GUO Lili, QI Lin, et al. Time-hopping multiple access performance of ultra-wideband system based on parallel combinatory spread spectrum[J]. Journal of South China University of Technology: Natural Science Edition, 2011, 39(9).

[3] JIANG Xiaofei, GUO Lili, WANG Bailing, et al. Performance analysis for UWB system based on parallel combinatory spread spectrum using different pseudo noise sequences[C]// International Conference on Education Technology and Computer. Shanghai: IEEE Computer Society, 2010: 213-216.

[4] 朱近康. 扩展频谱通信及应用[M]. 合肥: 中国科技大学出版社, 1993: 57-63.

ZHU Jiankang. Spread spectrum communication and application[M]. Hefei: University of Science and Technology of China Press, 1993: 57-63.

[5] 郭黎利, 姜晓斐, 齐琳, 等. 并行组合扩频超宽带发射参数对接收性能的影响[J]. 中南大学学报: 自然科学版, 2012, 43(6): 2185-2188.

GUO Lili, JIANG Xiaofei, QI Lin, et al. Influence on receiver performance by transmitter parameters in ultra-wideband system based on parallel combinatory spread spectrum[J]. Journal of Central South University: Science and Technology, 2012, 43(6): 2185-2188.

[6] GUO Lili, LI Beiming. BER performance of complex parallel combinatory spread spectrum communication system[C]// Wireless Communications, Networking and Mobile Computing. Shanghai: IEEE Computer Society, 2007: 1365-1368.

[7] 王玫, 曹明, 阳斌. 短波并行组合扩频通信系统研究[J]. 船舶电子工程, 2009, 29(11): 79-82.

WANG Mei, CAO Ming, YANG Bin. Study of HF parallel combinatorial spread spectrum systems[J]. Ship Electronic Engineering, 2009, 29(11): 79-82.

[8] LI Beiming, GUO Lili, QI Xiaodong. Complex position code parallel combinatory spread spectrum communication system with FEC technique[C]//Communications and Mobile Computing. Kunming: IEEE Computer Society, 2009: 209-213.

[9] Sasaki S, Kikuchi H, ZHU Jin-kang, et al. Performance of differential multiphase parallel combinatory spread spectrum communication system[C]//Communication Technology Proceedings. Beijing: Publishing House of Electronics Industry. 1996: 591-594.

[10] 齐晓东, 孙志国, 罗倩, 等. 基于循环相关技术的并行组合扩频信号检测算法[J]. 哈尔滨工程大学学报, 2009, 30(2): 215-218.

QI Xiaodong, SUN Zhiguo, LUO Qian, et al. Improved detection algorithm for parallel combinatory spread spectrum signals[J]. Journal of Harbin Engineering University, 2009, 30(2): 215-218.

[11] 李北明. 并行组合扩频通信系统关键技术的研究[D]. 哈尔滨: 哈尔滨工程大学信通学院, 2004: 6-8.

LI Beiming. The research of key technology of parallel combinatory spread spectrum communication system[D]. Harbin: Harbin Engineering University. College of Information and Communication Engineering, 2004: 6-8.

[12] 衣强. 并行组合扩频系统抗干扰技术及映射算法研究[D]. 哈尔滨: 哈尔滨工程大学信通学院, 2007: 2-8.

YI Qiang. The research on the PCSS anti-jamming performance and mapping method[D]. Harbin: Harbin Engineering University. College of Information and Communication Engineering, 2007: 2-8.

[13] 朱近康, 冯明臣. 并行组合扩频通信的数据调制映射算法和安全通信协议方式[J]. 电子学报, 1993, 21(1): 59-66.

ZHU Jinkang, FENG Mingchen. Data mapping modulation and security protocol of parallel combinatory SS communication[J]. Chinese Journal of Electronics, 1993, 21(1): 59-66.

[14] 王玫, 郭黎利, 于奇. 基于改进r-组合映射编码并行组合扩频通信系统的分析[J]. 船舶电子工程, 2008, 28(10): 78-81.

WANG Mei, GUO Lili, YU Qi. Analysis of coded parallel combinatory spread spectrum communication system based on improved r-combinatory mapping[J]. Ship Electronic Engineering, 2008, 28(10): 78-81.

[15] 郭黎利, 衣强, 李北明. 基于r-组合的并行组合扩频通信研究[J]. 无线电通信技术, 2007, 33(4): 25-27.

GUO Lili, YI Qiang, LI Beiming. Parallel combinatory spectrum communication system based on r-combinatory and the study of PN sequences[J]. Radio Communications Technology, 2007, 33(4): 25-27.

(编辑  邓履翔)

收稿日期：2012-08-15；修回日期：2012-10-17

基金项目：国家自然科学基金资助项目(61101141)

通信作者：刘明夺(1984-)，女，黑龙江哈尔滨人，博士研究生，从事并行组合扩频系统、伪随机码方面的研究；电话：13796023197；E-mail: xiaoduo_911@163.com