J. Cent. South Univ. (2017) 24: 1560-1572

DOI: 10.1007/s11771-017-3561-2

Adaptive threading strategy based on rolling characteristics analysis in hot strip rolling

PENG Wen(彭文)¹, CHEN Shu-zong(陈树宗)¹, GONG Dian-yao(龚殿尧)¹,

LIU Zi-ying(刘子英)², ZHANG Dian-hua(张殿华)¹

1. State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China;

2. Research Institute of Technology, Shougang Group, Beijing 100041, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: In order to improve the threading stability and the head thickness precision in tandem hot rolling process, an adaptive threading strategy was proposed. The proposed strategy was realized by the rolling characteristics analysis, and factors which affect the rolling force and the final thickness were determined and analyzed based on the influence coefficients calculation process. An objective function consisting of the influenced factors was founded, and the disturbance quantity was obtained by minimizing the function with the Nelder-Mead simplex method, and the proposed adaptive threading strategy was realized based on the calculation results. The adaptive threading strategy has been applied to one 7-stand hot tandem mill successfully, actual statistics data show that the predicted rolling force prediction in the range of ±5.0% is improved to 97.8%, the head thickness precision in the range of ±35 μm is improved to 98.5%, and the threading stability and the head thickness precision are enhanced to a high level.

Key words: hot strip rolling; adaptive threading; rolling characteristics analysis; influence coefficients method; simplex algorithm

1 Introduction

At the present time, as the requirement of dimensional precision, especially thickness precision of hot strip steel, is becoming stricter, how to improve thickness control precision has become a popular topic [1-3]. During the thickness control process, the precision of the strip head is the key factor for the thickness precision of the full length, also it is advantageous for the implement of the automatic gauge control system. The self-learning method and the adaptive threading technology have been proposed and applied to improve the precision of the thickness in the actual rolling process.

As a typical method, the self-learning method is used in most hot strip mills, and the current measured data was used to modify the model parameters. Series of ideas and strategies have been proposed in the last few decades [4-12]. WAN et al [4] described a self-learning model for steel rolling process, the model classification and information system classification were applied, meanwhile, a rolling strategy optimized method was founded, and the fitness of multi-varieties and multi- standards were solved greatly. BAMBACH et al [5] proposed a rolling force self-learning strategy in the multi-pass hot rolling processes, the coupled microstructure and flow stress model were used to predict the rolling force. A deep research on the function of short and long self-learning models was carried out, multi-variable control exponential smooth model was proposed in the short learning process, and the condition judgment strategy about the changing standard was joined into the long self-learning, also the tendency learning modulus method was introduced to the learning process which reduced the launch times and ensured the model continuity [6]. An optimized roll-gap self-learning algorithm in hot strip mill was proposed by PENG et al [7], the data collection, processing and looper speed compensation were taken into consideration, and the Newton-Raphson method was used to solve the thickness deviation function, and the spring equation was modified finally. In gauge-meter self-learning model proposed by HU et al [8], the effect of elastic deformation was taken into consideration, and the theory of the influence function method was adopted, a novel model based on the impact of roll elastic deformation on the gap setting by data fitting was founded, and the variation caused by the rolling condition was analyzed finally. However, the self-learning method can only improve thickness precision of adjacent strip, it is a typical feedback control method, and the thickness precision of current strip head cannot be adjusted.

Another approach used to enhance the thickness precision of the strip head is the adaptive threading technology, which uses the measured data from threaded stands to predict the material yield stress deviation to modify the schedule for the unthreaded stands. Numerous researchers have tried to show how the adaptive threading technology works during the last few years. HU [9] described the principle of the adaptive strip threading model for hot strip mill, he also studied the reasons for the distortion of rolling force prediction, and the backward prediction algorithm was proposed to modify the average yield stress deviation, the combined control strategy with gap and velocity modification were proposed to enhance the thickness precision of the strip head. ZHANG et al [10] proposed a dynamic threading strategy by combination of expert experience and fuzzy identification, which was developed by using fuzzy control technology. It deduced the origin of thickness deviation from the polarity of deviation between the predicted and actual ones in the first two stands, and the downstream gap positions were adjusted dynamically, which improved thickness accuracy of strip head. DING et al [11] analyzed the causes of head thickness deviation during the threading process, with the help of the P-H curve, he proposed an adaptive threading method by using measured data from threaded stands to predict the yield stress deviation, and the setup schedule of the remaining unthreaded stands was obtained. JI et al [12] gave an optimized threading strategy, in his work, a series of linear equation was set up to calculate the rolling force deviation, the thickness deviation in each stand was included, and the least square method was used to solve the equations, and the validity of the model was verified in the practical application. In the adaptive method mentioned above, the reasons of the rolling force deviation were attributed to the predicted deviation of the rolling force model, but in most time, for some reasons, like no thickness gauge in the rough mill exit to measure the intermediate slab thickness, the finishing rolling schedule was calculated from the original PDI data, the rolling force deviation originated from the deviation between the PDI data and the actual data, for this reason, the model self-learning model would have an opposite effect.

In this work, the plastic-elastic thickness curves and the rolling characteristics were used to analyze the rolling force deviation, with the rolling characteristics analysis, the influence coefficients were obtained, and the impact of the influenced factors on the rolling force and the thickness of each stand was described, and the objective function was established based on the minimum deviation of predictive rolling force, the Nelder-Mead simplex algorithm was used to solve the objective function, finally the disturbance quantity was obtained and the optimized threading model was proposed, and the target optimization schedule of the downstream stand was obtained, the threading stability and thickness control accuracy were guaranteed, the precision of the rolling force and the thickness was enhanced.

2 Analysis of thickness deviation based on spring equation

During hot strip rolling process, the spring equation is used to describe the relationship between the final thickness and the influence parameters [13, 14]. The final thickness (h) equals the sum of the rolling gap position and the mill stretch:

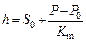                              (1)

where S₀ is the rolling gap position, mm; P is rolling force, kN; P₀ is zeroing rolling force, kN; K_m is the mill stiffness, kN/mm.

From Eq. (1), it is known that the main factors affecting final exit thickness are gap position S₀, actual rolling force P and mill stiffness K_m. The mill stiffness is considered as an unchanged factor with a certain strip width, and the gap position keep stationary before the automatic gauge control system start to work, so factors which influence the rolling force will influence the final thickness. From the rolling force model, it is known that the thickness fluctuation, temperature fluctuation and the chemical composition fluctuation are the disturbance factors. The thickness can affect the geometry of the deformation zone, and the temperature and the chemical composition fluctuation can influence the yield stress.

The impacts of the thickness and the temperature fluctuation are shown in Figs. 1 and 2. When the thickness fluctuation occurs, the strip plastic curve H changes to H′, the thickness of the intermediate slab changes from H₀ change to _, meanwhile the mill elastic curve keeps stationary, and the final thickness is changed from h to h′. When the temperature of the intermediate slab changes, the following yield stress changes, the strip plastic curve H changes to H″, and the plastic coefficient changes from tanθ to tanθ′, meanwhile the mill elastic curve keeps stationary, so the final thickness is changed from h to h″.

Fig. 1 Impact of thickness fluctuation on exit thickness

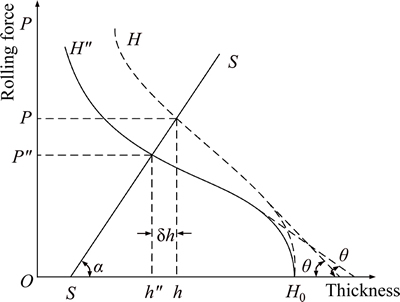
Fig. 2 Impact of temperature fluctuation on exit thickness

3 Analysis of rolling force deviation based on rolling characteristics

In order to enhance the thickness precision of the final strip, the thickness and the yield stress fluctuation caused by temperature fluctuation should be analyzed firstly. For most traditional hot rolling plants, there is no thickness gauge-meter in the delivery side of the rough mill for cost considerations, so the actual thickness fluctuation could not be detected, so the thickness of intermediate slab in PDI (the desired results of the set-up model) and the actual thickness are different more or less. Meanwhile, because of the oxide scale, the actual temperature of the intermediate slab cannot be obtained accurately from the surface temperature measured by the pyrometer in the entrance. In order to analyze the influence of the two factors, the rolling characteristics analyses were adopted for the deviation quantification process.

3.1 Increment equations

The comprehensive analytic method is used to analyze the impact of the rolling character on the final thickness and the rolling force [15], and in this method, the linearization of nonlinear function in a small range is applied to overcome the difficulties of solving a large number of nonlinear equations. Take the nonlinear function y=f(x₁, x₂) as an example, the Taylor series expansion in point (x₀₁, x₀₂) is expressed as

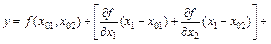
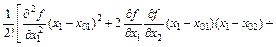
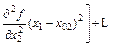                      (2)

And the increment equation can be further simplified as

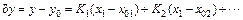
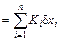                             (3)

where y₀=f(x₀₁, x₀₂);.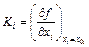

In order to analyze the impact of disturbance quantity and control quantity on the product quality, the static comprehensive analysis incremental models are established, the influence coefficient 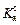 is used to describe the influence degree, parameter a is disturbance quantity or control quantity, b is the target quantity. So the rolling force increment equation and the spring increment equation are described as

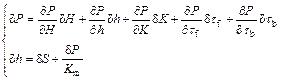 (4)

The thickness increment equation can be simplified as

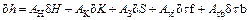      (5)

where A_H is the influence coefficient of initial thickness on thickness,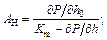 A_S is the influence coefficient of gap on thickness, A_K is the influence coefficient of yield stress on thickness,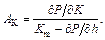

And the rolling force increment equation can be described as

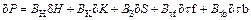      (6)

where B_H is the influence coefficient of initial thickness on rolling force, 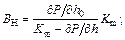 B_S is the influence coefficient of gap on rolling force,  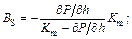B_K is the influence coefficient of yield stress on rolling force,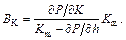

During the typical micro-tension rolling process, the strip tense fluctuation δτ_f and δτ_b could be controlled and maintained a small value, and with the help of the hydraulic gap control system (HGC), the gap position is stable at set value [16, 17], so the increment equations of the thickness and the rolling force are functions of thickness fluctuation and yield stress fluctuation caused by the temperature, these are consistent with the analysis of the previous p-h chart.

In the calculation of partial differential coefficient in influence coefficient, the secant method is used, as shown in Fig. 3. Take 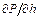as example，with the exit thickness fluctuation 0.01h_i, the new rolling force P is calculated, and the partial differential coefficient is described as

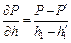                                 (7)

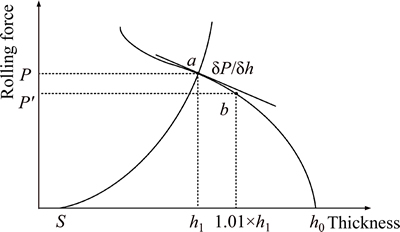
Fig. 3 Schematic of secant method

and 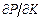 could be calculated with the secant method, and a series of partial differential coefficient from the final thickness 2.00 mm to 7.00 mm is calculated, Table 1 lists the typical rolling schedule and the partial differential coefficient of 3.00 mm.

3.2 Discussion of influence coefficient analysis

With the partial differential coefficient obtained, the influence coefficients are calculated by Eqs. (5) and (6), the following sections are taken to analyze the impact of the initial thickness fluctuation and the yield stress fluctuation (temperature fluctuation) on the rolling force separately.

3.2.1 Influence of initial thickness fluctuation

In order to study the impact of the initial thickness fluctuation δH₀ on the rolling force of stand i (described as P_i), the impact of initial thickness fluctuation on the inlet thickness δH_i should be calculated firstly, the thickness influence coefficient 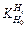 can be described as

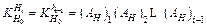            (8)

Secondly, the impact of inlet thickness on the rolling force of stand i is calculated, the rolling force influence coefficient 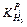lead by δH₀ could be described as

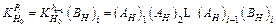  (9)

The rolling force fluctuation δP_i caused by the initial thickness fluctuation can be expressed as

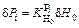                              (10)

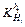
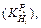
The influence coefficients 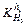and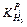of the thickness 2.00, 3.00, 4.00, 5.00, 6.00 and 7.00 mm are calculated with the method discussed in Section 2.2. Figure 4 shows the influence coefficient of inlet thickness on the outlet thickness 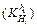and the rolling force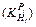with the thickness fluctuation δH_i=1.00 mm. Point A 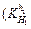or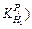 means that for thickness 7.00 mm, when the inlet thickness of stand F5 changes with δH₅=1.00 mm, the fluctuation of the outlet thickness is about 0.1 mm, meanwhile, the rolling force changes about 580 kN. And the trends of the six different specifications are similar, as the thickness increases, the impact of the inlet thickness fluctuation on the outlet thickness and the rolling force decreases. For stands from the upstream to the downstream, the impact of inlet thickness on the current outlet thickness (or rolling force) increases. For the first stand, the influences are nearly the same, but for the last stand, the influence coefficient for h=2.00 mm is about 30%, higher than that of h=7.00 mm.

Table 1 Value of partial differential coefficients (3.00 mm)

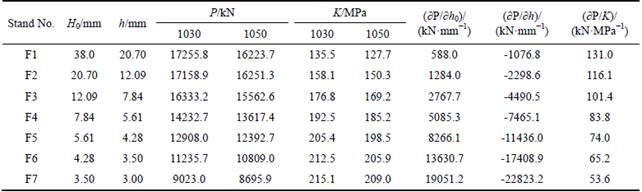
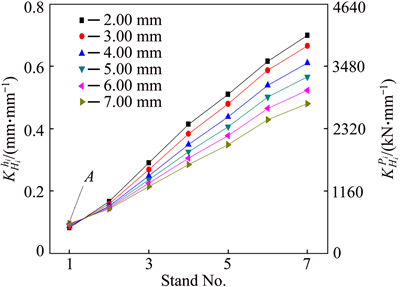
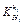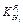Fig. 4 and with thickness fluctuation δH_i=1.00 mm

Figure 5 shows the impact of initial thickness fluctuation on each outlet thickness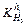 with the thickness fluctuation δH₀=1.00 mm. Point B 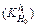means for thickness 7.00 mm, when the intermediate slab thickness changes with δH₀=1.00 mm, the outlet thickness fluctuation of stand F1 is about 0.095 mm. It can be seen that the 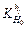decreases as rolling pass increases for all specifications. And the impact of the initial thickness fluctuation on the first three stand decreases drastically, but for the following stands, the curves change smoothly close to 0, and nearly no fluctuations, in other words, the impact of the thickness fluctuation of the intermediate slab on the outlet thickness is limited to the first three stands. As the product target thickness increases, the difference is not big, within the scope of 0.02 mm, and the maximum valve appears in stand F1.

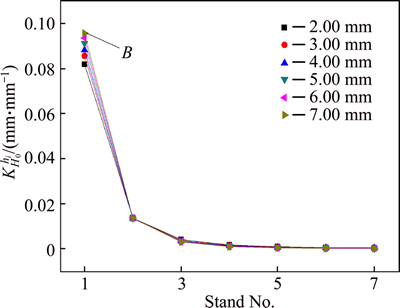
Fig. 5 Trend of with δH₀=1.00 mm

Figure 6 shows the impact of initial thickness fluctuation on each rolling force 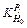 with the thickness fluctuation δH₀=1.00 mm. Point C 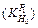means for thickness 7.00 mm, when the initial intermediate slab thickness changes with δH₀=1.00 mm, the rolling force fluctuation of stand F1 is about 552 kN. As shown in Fig. 6, for stands from the upstream to the downstream, all the trends of  are similar as the impact of the initial thickness on the outlet thickness for all specifications. The impact of the intermediate slab thickness fluctuation on the rolling force is limited to the first three stands. For stands after F4, the fluctuation of the rolling force is less than 20 kN which can be ignored.

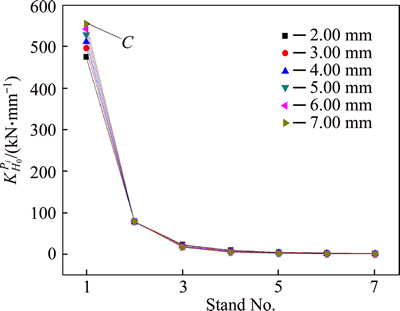
Fig. 6 Trend of 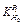with δH₀=1.00 mm

3.2.2 Influence of initial yield stress fluctuation

The yield stress fluctuation caused by temperature fluctuation (δT₀) of the intermediate slab will not disappear when the rolling passes increase, and the yield stress fluctuation δK_i caused by δT₀ appears in each stands. Different from the thickness influence, the yield stress fluctuation of current stand cannot only affect the rolling force itself, it also effects the rolling force of the following stands through changing the outlet thickness of the current stand.

Therefore, in order to study the impact of the yield stress fluctuation on the rolling force, the following steps are carried out. Firstly, taking into account the genetic effect of the yield stress, the relationship between the initial and the following yield stress fluctuation meet δK_i=ψ_iδK₀, and the impact of the current yield stress fluctuation on the rolling force of the stand i is described as

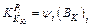                             (11)

where ψ_i is the yield stress genetic coefficient.

Secondly, the impact of yield stress on the inlet thickness of the stand i (the exit thickness of stand i-1) can be given as

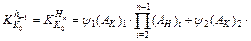
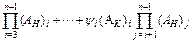
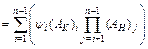               (12)

Thirdly, the impact of inlet thickness lead by the yield stress on rolling force of stand i can be described as

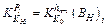                          (13)

So the total impact of yield stress fluctuation δK₀ on rolling force of stand i could be described as

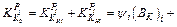
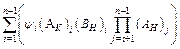         (14)

The rolling force fluctuation δP_i caused by the initial temperature fluctuation can be expressed as

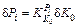                              (15)

And the initial yield stress fluctuation δK₀ on the final thickness can be described as

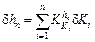                           (16)

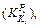
The influence coefficients 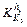and of the thickness 2.00, 3.00, 4.00, 5.00, 6.00 and 7.00 mm are calculated with the method discussed in Section 3.1.

In order to analyze the impact of the initial temperature fluctuation on yield stress of each stand, the initial temperature fluctuation δT₀=20.0 °C is added for the schedule calculation (like in Table 2), as shown in Fig. 7, in this condition, the temperature deviation in stand F4 is 12.0 °C (point D₁), and the yield stress deviation is about 7.4 MPa (point D₂). It is shown that the yield stress deviation exists in each stand, as the rolling pass increases, the temperature deviation and the yield stress deviation decrease, as the target thickness increases from 2.00 to 7.00 mm, the temperature deviation and yield stress deviation increase. It also shows that the yield stress fluctuation caused by the initial temperature fluctuation exists in each pass.

The impact of the yield stress on the outlet thickness of the current stand is shown in Fig. 8, and the impact of the yield stress on the rolling force 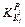is included. Point D 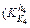or 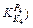means for thickness 2.00 mm, when the yield stress fluctuation changes with δK₂=1.00 MPa, the fluctuation of the outlet thickness is about 0.006 mm, meanwhile, the rolling force fluctuation is about 31 kN. For all different specifications, as the rolling pass increases, the impact of the yield stress fluctuation on the outlet thickness and the rolling force decreases. The thinner the thickness, the faster the amplitude, for the first three stands, the influence coefficient of 2.00 mm is bigger than that of the 7.00 mm, but for the last stand, the influence coefficient of 2.00 mm is smaller than that of the 7.00 mm.

The impact of the initial temperature fluctuation on the outlet thickness of each stand 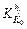 is shown in Fig. 9. Point F 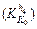gives the outlet thickness fluctuation of stand F4 for thickness 2.00 mm, when temperature fluctuation changes with δT₀=20.0 °C, the thickness fluctuation of F4 is about 0.09 mm, and the thickness fluctuation will affect the rolling force of F5. It shows that for the six different specifications, as the rolling pass increases, the impact of the initial temperature fluctuation on the outlet thickness decreases. The thinner the thickness, the greater the impact. For thickness 2.00 mm, when δT₀=20.0 °C, the final thickness of the product is about 0.055 mm.

The rolling force fluctuation δP_i caused by the thickness deviation lead by the initial temperature fluctuation can be obtained easily by Eq.(13), as shown in Fig. 10, with the rolling pass increases, the trend of the rolling force fluctuation increases firstly, then tends to be stable. Similarly, the thinner the thickness, the greater the impact. For thickness 2.00 mm, the rolling force fluctuation of F4 (point G) is about 275 kN. As the results shown in Figs. 7 and 10, the total rolling force fluctuation caused by the initial temperature δT₀=20.0 °C is obtained, as shown in Fig. 11. Compared with Fig. 10, the trends of both curves are similar, only for the first stand, because the initial temperature fluctuation cannot affect the thickness of intermediate slab, the rolling force deviation in stand F1 is from the yield stress fluctuation entirely.

Table 2 Comparison of rolling force between actual and the predicted ones

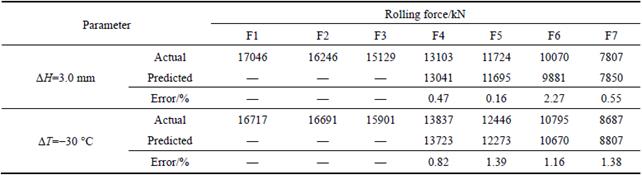
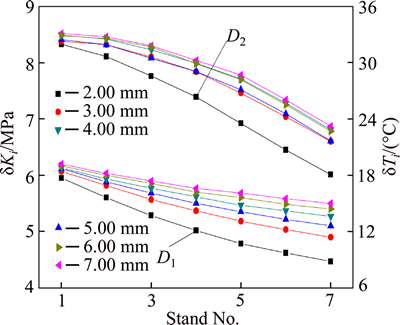
Fig. 7 δK_i and δT_i with δT₀=20.0 °C

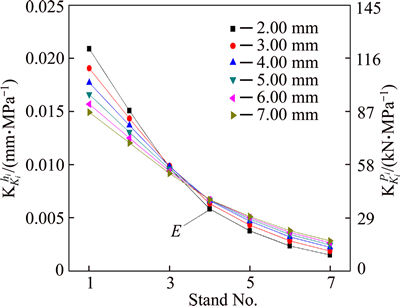
Fig. 8 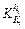and with δT₀=20.0 °C

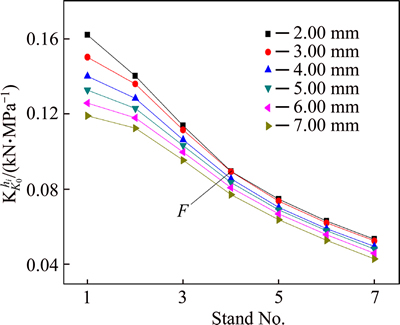
Fig. 9 Trend of 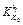with δT₀=20.0 °C

4 Realization of adaptive threading strategy

The influences of thickness and temperature fluctuation are reflected in the deviation of the rolling force during the rolling process, so the actual fluctuation could be obtained by Eqs. (10) and (15), based on which the adaptive threading strategy is proposed. It is designed as a sub-model of thickness setup model, and realized by Visual Studio 2008. The following section shows the detailed steps of the adaptive threading strategy. The flow chart of adaptive threading strategy is shown in Fig. 12.

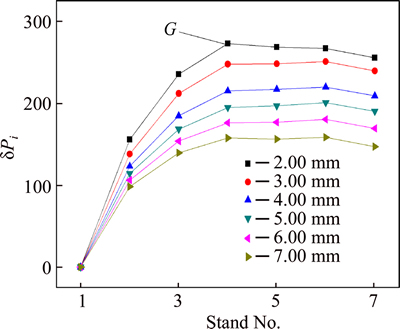
Fig. 10 Trend of 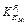with δT₀=20.0 °C

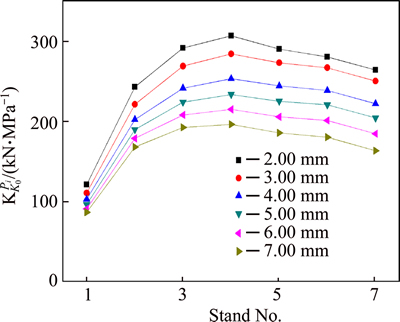
Fig. 11 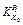with temperature fluctuation δT₀=20.0 °C

4.1 Threading adaption stands selection

Making full use of the actual measured data during the threading process helps to obtain a more accurate deviation. The selection strategy should not be limited to the first two stands, the number of adaptive stands should be obtained from the rolling specifications and the threading velocity. The data collection time, model calculation time, communication time and the hydraulic screwdown time should be taken into consideration. The typical mill automatic system is two levels, Level 1 is basic automatic control system, and Level 2 is process control system, the communication cycle between Level 1 and the Level 2 is about 100 ms [18], the total time required for the adaption calculation is about 1000 ms (10 sampling point), and the data collection and the processing of each stand are executed simultaneously; the hydraulic screwdown time of the roll gap is less than 100 ms for changing 0.25 mm [19]. The data collection stand named sampling stand, and the surplus downstream stands named adaptive stand. Take the target thickness h=3 mm for example, the threading velocity is 8.0m/s, Fig. 13 gives the head position while bite and threading adaption finish.

Fig. 12 Flow chart of optimized thread adaption process

As shown in Fig. 13, when stand F2 is taken as the end sampling stand and the hydraulic screwdown under the adaptive threading schedule finishes, the strip head has not reached the stand F3, time to the roll gap adjustment is sufficient, and if F5 is chosen as the end sampling stand, the strip head has reached the F7 stand, the threading process has been finished, it is unable to complete the adjustment obviously. For h=3 mm, the optimal sampling stand is three (F1-F3), and the surplus downstream stands F4-F7 could be modified. So for different specifications, the sampling stand is determined by comparing the differences between of threading time and the final screwdown time in each stand.

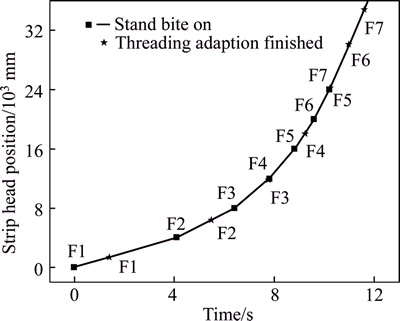
Fig. 13 Schematic of strip head position with complete adaptive threading

4.2 Deviation solved with objective function

4.2.1 Objective function

The solution strategy is realized by the minimum of the objective function [20-23], in which the thickness deviation and the temperature deviation are taken as the disturbance characters, and the objective function is founded with the predicted and the actual rolling force, the objective function is given by

             (17)

where z is the decision variable vector; i is the sampling stand number; n is the end sampling stand; 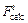is the predicted rolling forces based the disturbance characters; is the actual rolling forces; k_i is weight distribution coefficient of each stand.

4.2.2 Nelder-Mead simplex method

In the objective function solution process, the Nelder-Mead simplex method is usually used to find a local minimum of the unconstrained nonlinear function of n variables [24-27]. Four operations may be accomplished in solution process: reflection, expansion, contraction and shrinking, as illustrated in Fig. 14, for an example of two variables. The algorithm proceeds in the following steps:

1) Sorting: calculate the valve of initial points of z₁, z₂, …, z_i …, z_n, the best point z_b contains 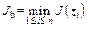and the worst point z_w contains 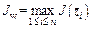, and the function value contains J_bn< J_w. The central point can be obtained as

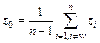                           (18)

2) Reflection: the reflection point z_r is obtained from the central point z₀, as shown in Fig. 14(a):

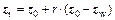                         (19)

where r is the reflection coefficient, by assuming the step r=1.

If 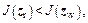then z_w is replaced by z_r and the process is restarted.

3) Expansion: if 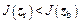meets, the expansion point z_e is obtained with respect to z₀ along the z_r-z₀ direction, as shown in Fig. 14(b):

                         (20)

where e is the expansion coefficient, by assuming the step e=2.

if 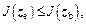then z_w is replaced by z_e and a new process is restarted.

4) Contraction: if 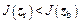is false，and it meets the condition , then z_w is replaced by z_r and a new process is restarted; else 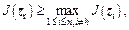the following two cases are discussed:

(a) Internal contraction: if 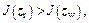then point z_r should be ignored and the contract z_w-z₀, as shown in Fig. 14(c), the contraction point z_c is given:

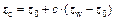                         (21)

where c is internal contraction, by assuming the step c=0.5;

if 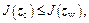then z_w is replaced by z_c and a new process is restarted; else, there is no optimized point in the z_r-z₀ direction, the Step 5) should be carried out.

(b) External contraction: if 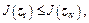then z_r-z₀ should be contracted, as shown in Fig. 14(d):

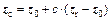                         (22)

where c is internal contraction, by assuming the step c=0.5;

if 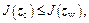then z_w is replaced by z_c and a new process is restarted; else, there is no optimized point in the z_r-z₀ direction, then Step 5) should be carried out.

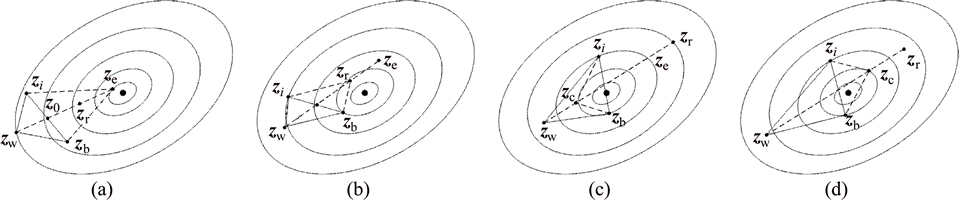
Fig. 14 Schematic diagram of basic operation in simplex algorithm

5) Shrinking: if the contraction point is not better than the worst point, then the simplex is shrunk toward the best point, the vertices except the best point will be replaced by

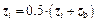, i=1, …, n                  (23)

6) Stop criterion: a new simplex is formed by replacing the worst point or shrinking. Recalculate the function values and search the best point and the worst point. If the following convergence criterion is reached, then stop iteration and point z_b is the optimal solution of objective functions; if the maximum number of iterations is reached or the convergence criterion is not reached, go to reflection step for further iteration.

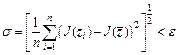                (24)

where is the average valve,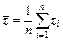and ε is the permissible error.

4.2.3 Initial values initialization

As shown in Eqs. (9)-(10) and Eqs. (14)-(15), the cost function involves 8 variables. So, the number of simplex vertexes is 9. The initial vectors of the 9 simplex vertexes are given as

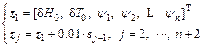            (25)

where n is the end sampling stand; z_j is the vector of the jth simplex vertex; s_j is the step vector;

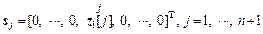   (26)

where z₁[j] is the jth component of vector z₁.

Figure 15 gives the convergence curve of Nelder- Mead (N-M) simplex algorithm during the solution of the objective function, it shows that objective function converges rapidly which can fully meet the demand of online application.

4.3 Schedule re-calculation

With the initial thickness deviation and the temperature deviation calculated by the objective function, the initial thickness fluctuation and the temperature fluctuation of the intermediate slab could be obtained accurately, also the thickness fluctuation and the yield stress fluctuation in exit of the end sampling stand could be obtained, and the schedule of the surplus downstream stands could be calculated based on the modified thickness and temperature. The calculation work is realized in Level 2, and the detailed calculated process is introduced [28, 29].

Fig. 15 Convergence curve of N-M simplex algorithm

5 Industrial tests and application

5.1 Plant description

In the present work, in order to verify the validity of proposed method, a series of industrial tests are carried out in a plant which is a 1700 mm 7-stand hot tandem mill. Each stand is equipped with two single cylinders mounted on the top, which can perform the regulation of the roll gap either in position or in force. Meanwhile, in the entrance and the delivery side, two pyrometers are used for the temperature measurement, and the final thickness is given by the X-ray thickness gauge. Figure 16 shows the layout of this hot tandem mill.

The processed material mainly consists of Q235B, Q345B, 65Mn, etc, the hot tandem mill can reduce the strip from the mid-slab thickness with 35.0-48.0 mm to a final gauge 1.5-8.0 mm, and the coil width range is 950-1550 mm. The temperature at the entrance is 980-1020 °C.

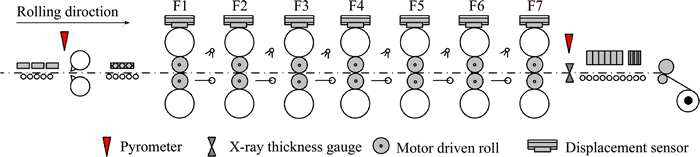
Fig. 16 Layout of 1700 mm 7-stand hot tandem mill

5.2 Industrial tests and results analysis

The following tests are carried out to verify the actual effect of the adaptive threading strategy: 1) thickness fluctuation test and 2) temperature fluctuation test. During the tests process, in order to minimize the impact of roll thermal expansion on the target thickness as far as possible, the adjacent pieces of strip in the stable rolling process are chosen to compare the effect, at this time the temperature distribution and the thermal expansion tend to balance, and the work roll wear of one strip could be ignored.

The thickness fluctuation is realized by changing the gap position of the last pass in the rough rolling, and the temperature fluctuation is realized by extending the residence time in the intermediate table, and the actual temperature fluctuation could be detected by the pyrometer at the entrance. For the adjacent pieces of strip, the actual rolling schedule remains. Also in order to avoid the impact of the gap screwdown on the actual rolling force, the adaptive threading schedule is not implemented. The actual and predicted rolling forces of the adjacent pieces are shown in Figs. 16 and 17.

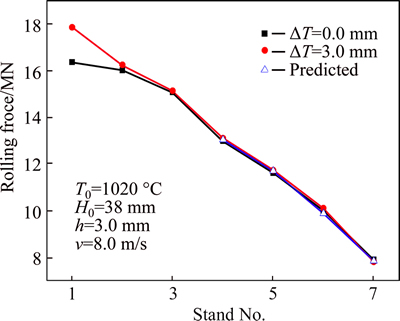
Fig. 17 Comparison of rolling force in adjacent pieces

Figure 17 shows the comparison of the rolling force under the thickness fluctuation (ΔH=3.0 mm), it shows that for the adjacent pieces, the deviation of rolling force occurs in the upstream stands (F1 and F2), and the rolling force of the downstream stands (F4-F7) with ΔH=3.0 mm is much closer to the rolling force with ΔH=0.0, it is consistent with the results of the analysis in Section 3.2.1.

Figure 18 shows the comparison of rolling force under the temperature fluctuation (ΔT=-30 °C), it seems that the rolling force of all stands are higher than the initial ones, and the genetic effect is obvious, and the predicted rolling force of the downstream stands (F4-F7) is closed to the actual ones. The predicted errors of the rolling force are shown in Table 2. It can be seen that the precision errors of rolling force with the adaptive threading process is less than 2.3%.

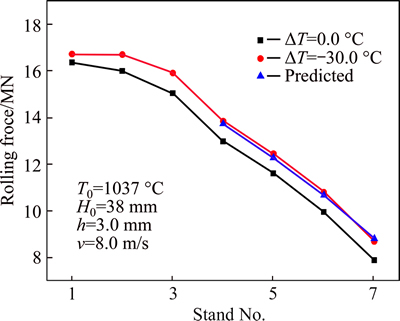
Fig. 18 Power distributions for different schedules

The contrast tests (ΔH=3.0 mm and ΔT=-30 °C) are implemented with adjacent pieces to verify the control effect, the first piece was rolled with the initial rolling schedule, the thickness and temperature fluctuation are not taken consideration, the second piece is rolled with the proposed adaptive threading strategy. The precision of the final thickness are shown in Figs. 19 and 20.

Fig. 19 Final thickness precision with initial thickness fluctuation ΔH=3.0 mm

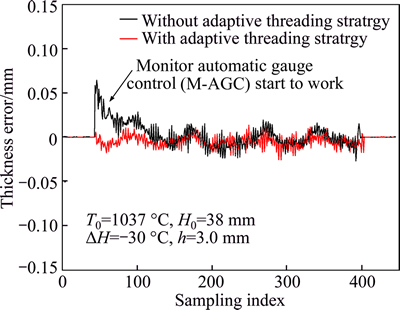
Fig. 20 Final thickness precision with initial temperature fluctuation ΔT=-30 °C

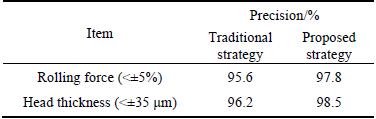
It can be seen that the strip thickness control precision is enhanced effectively with the proposed adaptive strategy, the impact of the thickness and temperature fluctuation on the final thickness is weakened. As shown in Fig. 18, the initial thickness fluctuation has little effect on the final thickness, Fig. 19 shows that the impact of the initial temperature fluctuation on the final thickness is greater than 35 μm for ΔT=-30 °C, which cannot be ignored. The results of comparative statistics data of two adjacent months are shown in Table 3, the rolling force prediction hit rate of the strip head in the range of ±5.0% is improved from 95.6% to 97.8%, and the head thickness precision in the range of ±35 μm is enhanced from 96.2% to 98.5%. The comparison results show that the proposed approach is an efficient way to enhance the control precision for hot tandem mill.

Table 3 Control precision comparison between traditional and proposed strategy

6 Conclusions

1) The key factors of the target thickness deviation are the initial thickness and temperature fluctuation. As the rolling pass increases, the impact of the initial thickness fluctuation on the thickness (or the rolling force) of each pass can be ignored, and the impact of the initial temperature fluctuation on the thickness (or the rolling force) of each pass shows a trend from rise to stable.

2) The thickness and temperature fluctuation is obtained by solving an objective function with the Nelder-Mead simplex method, and the adaptive threading strategy is proposed to modify the rolling schedule of the surplus downstream stands.

3) The proposed adaptive threading strategy has been applied successfully to the 7-stand tandem hot mill, and the application results show that the precision of the rolling force is improved significantly, and the thickness precision is enhanced to a higher level.

References

[1] LENARD J G. Primer on flat rolling [M]. Tokyo: Tokyo Press, 2007: 17-20.

[2] LINGHU Ke-zhi, He An-rui, YANG Quan, ZHAO Lin, GUO Xiao-Bo. Dynamic decoupling for combined shape and gauge control system in wide strip rolling process [J]. Journal of Iron and Steel Research, international, 2008, 15(2): 28-31.

[3] JI Ya-feng, ZHANG Dian-hua, CHEN Shu-zong, SUN Jie, LI Xu, DI Hong-shuang. Algorithm design and application of novel GM-AGC based on mill stretch characteristic curve [J]. Journal of Central South University, 2014, 21(3): 942-947.

[4] WAN Zhou, WANG Xiao-dong. WU Jian-de. Model adaptive learning for steel rolling mill control [C]// Proceedings of 2008 IEEE International Symposium on Knowledge Acquisition and Modeling Workshop. IEEE Xplore, 2008, 16(2): 903-906.

[5] BANBACH M., SEUREN S. On instabilities of force and grain size predictions in the simulation of multi-pass hot rolling processes [J]. Journal of Materials Processing Technology, 2015, 216: 95-113.

[6] WANG Jian, XIAO Hong, ZHANG Jing-xu. Research on self-learning of hot strip finishing setup model for rolling force [J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3398-3407. (in Chinese)

[7] PENG Wen, ZHANG Dian-hua, GONG Dian-yao Optimization of roll-gap self-learning algorithm in tandem hot rolled strip finishing mill [C]// Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC). IEEE Xplore, 2012: 3947-3950.

[8] HU Xina-lei, WANG Zhao-dong，ZHAO Zhong，LIU Xiang-hua, WANG Guo-dong. Gauge-meter model building based on the effect of elastic deformation of rolls in a plate mill [J]. Journal of University of Science and Technology Beijing, 2007, 14(4): 381-386.

[9] HU Song-tao. Study and application on adaptive strip threading model for hot strip mill [J]. Metallurgical Industry Automation, 2009, 33(4): 63-65, 70. (in Chinese)

[10] ZHANG Xiao-feng, WANG Zhe, WANG Guo-dong, LIU Xiang-hua. Fuzzy dynamic setting technology for hot strip mill [J]. Journal of Iron and Steel Research, 2000, 12(3): 22-26. (in Chinese)

[11] DING Jing-guo, HU Xian-Iei, JIAO Jing-min, SHE Guang-fu, LIU Xiang-hua. Application of adaptive threading technique to hot strip mill [J]. Journal of Iron and Steel Research, International. 2008, 15(5): 29-31, 36.

[12] JI Ya-feng, PENG Wen, Ma Geng-sheng, Zhang Dian-hua. Optimization of adaptive threading strategy in hot strip rolling [J]. Journal of Northeastern University(Natural Science). 2015, 36(8): 1106-1109. (in Chinese)

[13] PENG Wen, ZHANG Dian-hua, CAO Jian-zhao, LIU Zi-ying. Optimization algorithm of spring equation in tandem hot rolling based on static errors [J]. Journal of Northeastern University (Natural Science).2013, 34(4): 528-531. (in Chinese)

[14] HILL S, HUMPHREYS L D. Numerical mountain pass periodic solutions of a nonlinear spring equation [J]. Computers & Mathematics with Applications, 1998, 35(12): 59-67.

[15] SUN Yi-kang. Models and control in hot rolling process [M]. Beijing, Metallurgical Industry Press, 2007: 210-211.

[16] SUN Jie, CHEN Shu-zong, HAN Huan-huan, CHEN Xing-hua, CHEN Qiu-jie, ZHANG Dian-hua. Identification and optimization for hydraulic roll gap control in strip rolling mill [J]. Journal of Central South University, 2014, 22(6): 2183-2191.

[17] ZHANG Hao-yu, SUN Jie, ZHANG Dian-hua, LI Xu. Compensation method to improve dynamics of hydraulic gap control system [C]// Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC). IEEE Xplore, 2012: 1536-1541.

[18] CAO Jian-zha, PENG Wen, ZHANG Dian-hua. Multi-task application platform of process control system for hot strip rolling [J]. Journal of Northeastern University (Natural Science). 2013, 34(8): 1113-1117. (in Chinese)

[19] ZENG Liang-cai. Strip mill hydraulic agc synthetical test system and fault diagnosis research [D]. Wu Han: Wuhan University of Technology (School of Logistics Engineering), 2005.

[20] RICHARD O, EFSTRATIOS N P. Multi-objective optimization with convex quadratic cost functions: A multi-parametric programming approach [J].Computers and Chemical Engineering. 2016, 85: 36-39.

[21] JIA Shu-jin, LI Wei-gang, LIU Xiang-hua, DU Bin. Multi-objective load distribution optimization for hot strip mills [J]. Journal of Iron and Steel Research, international. 2013, 20(2): 27-32, 61.

[22] YAN Ji-hong, LI Lin. Multi-objective optimization of milling parameters e the trade-offs between energy, production rate and cutting quality [J]. Journal of Cleaner Production, 2013(52): 462-471.

[23] ABIDO M A. Multi-objective particle swarm optimization of environmental/economic dispatch problem [J]. Electric Power System Research, 2009, 79: 1105-1113.

[24] NELDER J A, MEAD R. A simplex method for function minimization [J]. Computer Journal, 1965, 7: 308-313.

[25] CHEN Shu-zong, CHEN Shu-zong, ZHANG Dian-hua, PENG Liang-gui, ZHANG Xin, SUN Jie, LIU Yin-zhong. Multi-objective optimization of rolling schedule based on cost function for tandem cold mill [J]. Journal of Central South University, 2014, 21(5): 1733-1740.

[26] PENG Wen, CHEN Shu-zong，Ding Jing-guo，ZHANG Dian-hua. Multi- objective function optimization of rolling schedule in tandem hot mill based on penalty item [J]. Journal of Shenyang University of Technology, Electric Power System Research, 2014, 36(1): 45-50. (in Chinese)

[27] OURIA A, TOUFIGH M M. Application of nelder-mead simplex method for unconfined seepage problems [J]. Applied Mathematical Modelling, 2009, 33(9): 3589-3598.

[28] RUDKINS N, EVANS P. Mathematical modelling of mill set-up in hot strip rolling of high strength steels [J]. Journal of Materials Processing Technology, 1998, 80/81: 320-324.

[29] WANG Jian, LIU Chang-qing, XIAO Hong. Research on finishing setup and self-adaptive of hot strip mill [J]. Journal of Central South University, 2012, 43(7): 2607-2612. (in Chinese)

(Edited by FANG Jing-hua)

Cite this article as: PENG Wen, CHEN Shu-zong, GONG Dian-yao, LIU ZI-ying, ZHANG Dian-hua. Adaptive threading strategy based on rolling characteristics analysis in hot strip rolling [J]. Journal of Central South University, 2017, 24(7): 1560-1572. DOI: 10.1007/s11771-017-3561-2.

Foundation item: Project(51504061) supported by the National Natural Science Foundation of China

Received date: 2016-03-21; Accepted date: 2016-05-11

Corresponding author: PENG Wen, PhD; Tel: +86-24-83685342; E-mail: pengwen233@163.com