Intelligent back-looking distance driver model and stability analysis for connected and automated vehicles
来源期刊:中南大学学报(英文版)2020年第11期
论文作者:曲栩 易紫薇 陆文琦 徐凌慧 冉斌
文章页码:3499 - 3512
Key words:linear stability; intelligent driver model; connected and automated vehicles
Abstract: The connected and automated vehicles (CAVs) technologies provide more information to drivers in the car-following (CF) process. Unlike the human-driven vehicles (HVs), which only considers information in front, the CAVs circumstance allows them to obtain information in front and behind, enhancing vehicles perception ability. This paper proposes an intelligent back-looking distance driver model (IBDM) considering the desired distance of the following vehicle in homogeneous CAVs environment. Based on intelligent driver model (IDM), the IBDM integrates behind information of vehicles as a control term. The stability condition against a small perturbation is analyzed using linear stability theory in the homogeneous traffic flow. To validate the theoretical analysis, simulations are carried out on a single lane under the open boundary condition, and compared with the IDM not considering the following vehicle and the extended IDM considering the information of vehicle preceding and next preceding. Six scenarios are designed to evaluate the results under different disturbance strength, disturbance location, and initial platoon space distance. The results reveal that the IBDM has an advantage over IDM and the extended IDM in control of CAVs car-following process in maintaining string stability, and the stability improves by increasing the proportion of the new item.
Cite this article as: YI Zi-wei, LU Wen-qi, XU Ling-hui, QU Xu, RAN Bin. Intelligent back-looking distance driver model and stability analysis for connected and automated vehicles [J]. Journal of Central South University, 2020, 27(11): 3499-3512. DOI: https://doi.org/10.1007/s11771-020-4560-2.

J. Cent. South Univ. (2020) 27: 3499-3512
DOI: https://doi.org/10.1007/s11771-020-4560-2
YI Zi-wei(易紫薇)1, 2, 3, LU Wen-qi(陆文琦)1, 2, 3, XU Ling-hui(徐凌慧)1, 2, 3,QU Xu(曲栩)1, 2, 3, RAN Bin(冉斌)1, 2, 3
1. School of Transportation, Southeast University, Nanjing 211189, China;
2. Joint Research Institude on Internet of Mobility, Southeast University and University of Wisconsin-Madison, Nanjing 211189, China;
3. Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies,Nanjing 211189, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: The connected and automated vehicles (CAVs) technologies provide more information to drivers in the car-following (CF) process. Unlike the human-driven vehicles (HVs), which only considers information in front, the CAVs circumstance allows them to obtain information in front and behind, enhancing vehicles perception ability. This paper proposes an intelligent back-looking distance driver model (IBDM) considering the desired distance of the following vehicle in homogeneous CAVs environment. Based on intelligent driver model (IDM), the IBDM integrates behind information of vehicles as a control term. The stability condition against a small perturbation is analyzed using linear stability theory in the homogeneous traffic flow. To validate the theoretical analysis, simulations are carried out on a single lane under the open boundary condition, and compared with the IDM not considering the following vehicle and the extended IDM considering the information of vehicle preceding and next preceding. Six scenarios are designed to evaluate the results under different disturbance strength, disturbance location, and initial platoon space distance. The results reveal that the IBDM has an advantage over IDM and the extended IDM in control of CAVs car-following process in maintaining string stability, and the stability improves by increasing the proportion of the new item.
Key words: linear stability; intelligent driver model; connected and automated vehicles
Cite this article as: YI Zi-wei, LU Wen-qi, XU Ling-hui, QU Xu, RAN Bin. Intelligent back-looking distance driver model and stability analysis for connected and automated vehicles [J]. Journal of Central South University, 2020, 27(11): 3499-3512. DOI: https://doi.org/10.1007/s11771-020-4560-2.
1 Introduction
Car-following (CF) model is one of the most significant microscopic traffic flow models that depict vehicles movement in microcosmic perspective, which have been developed for more than half of the century. Since the first CF model was introduced by PIPES [1], scholars have done a lot of works in this area and proposed a large number of CF models. Among them, most extensive applied models include Newell’s model [2], GHR model [3], Gipps model [4], optimal velocity (OV) model [5], intelligent driver model (IDM) [6],and full velocity difference (FVD) model [7].
A large number of modified models based on these models or other newly proposed models have been developed prosperously [8, 9]. Some of them are applied to control the platoon in the intelligent system. With the rapid development of sensing and communication technologies, the connected and automated vehicles (CAVs) technologies, including vehicle-to-vehicle (V2V) and vehicle-to- infrastructure (V2I) technologies, have evolved drastically over the last several decades [10]. Under the CAVs environment, vehicles could exchange information, make decisions more intelligent than that in the traditional environment [11], and use advanced technologies to acquire accurate information from big data [12]. The communication capability in such connected autonomous vehicles also enables cooperative platoon control strategies to achieve system level objectives through coordination across all or some of the vehicles in the platoon [13]. The car-following model is applied as the car-following model-based controller in controlling the CAV platoon. The controller to control the CAV platoon includes four types [14]: proportional-integral-derivative (PID) controller, car-following model-based controller, sliding mode controller, and model predictive controller. These controllers are based on a certain CF model, a specific optimal goal [15], or a linear/non-linear feedback control logic [16].
In the car-following model-based controller designing, information flow topology (IFT) is a key point. According to the researches, different information topologies can bring different effects for the same control logic, increase traffic throughput, linear stability, etc. There are many types of information flow topologies involved in the research of longitudinal control of CAVs, such as predecessor-following topology, predecessor- leader-following topology, two-predecessor- following topology, multiple-predecessor-following topology, and bidirectional topology [17]. Controllers are designed based on a specific IFT [18] or dynamical IFT for intelligent vehicles [19].
A lot of models based on different information flow topologies are developed, including macroscopic models [20-23] and microscopic CF models [24-28]. Among them, bidirectional topology shows a special vision of driving. The bidirectional IFT by which drivers not only follow the preceding vehicles but also consider the following vehicles to adjust its movement, is different from the others that alter the traditional idea of driving. In the traditional human driving environment, drivers only measure the traffic states through percept of the preceding vehicle, but rarely consider the speed, distance and other information of the following vehicle to optimize their own speed. In addition, most traditional CF models do not consider the information of following vehicles. An important reason is that the driver is limited in obtaining information, and they must pay attention to the changes of the preceding vehicle in real time, so they have less time to pay attention to the speed change of the following vehicle to adjust themselves own state. However, in the intelligent network environment, CAV can obtain abundant information from a variety of sources in real time, including information of all the front vehicles and following vehicles. Comparing with human driving, the CAV can optimize its speed state based on a variety of information by applying the improved IFT model established in the traditional environment.
The first back-looking CF model was proposed by HERMAN et al [29] based on the relative velocity (RV) model that the relative velocity between the target vehicle and the preceding vehicle, and the relative velocity between the target vehicle and the following vehicle have been considered. The local stability condition and string stability condition have been investigated. The result shows the stability improved with the increase of the proportional of the relative velocity of both preceding and following vehicles. NAKAYAMA et al [30] extended an OV model with desired speed of the preceding and following vehicle related to the distance between adjacent vehicles, and it conformed that the extended model performs better in traffic stability compared with OV model. HASEBE et al [31] proposed an extended OV model considering multiple vehicles preceding and one vehicle following. GE et al [32] extended OV model with an arbitrary number of vehicles preceding or following. SUN et al [33] extended the FVD model, considering an arbitrary number of preceding vehicles and one following vehicle. YANG et al [34] presented an extended OV model in which the information of an arbitrary number of preceding or following cars is considered. YANG et al [35] extended Gipps’ safe distance model, derived the stability conditions and found out that the drivers with smaller reaction time or larger additional delay can stabilize traffic flow. HOU et al [36] incorporated the FVD model with driver’s visual angle and found the stability conditions. CHEN et al [37] extended FVD model considering the driver’s sensory memory and derived the stability conditions of the new model. MA et al [38] proposed CF model based on the FVD, accounting for the time-delayed velocity difference and backward looking effect, and the result showed that it can strengthen the stability of traffic flow and suppress the traffic congestion.
To design the car-following model-based controller in the CAVs environment, the IDM unified the free flow state and congested flow state of traffic into one equation, and the acceleration changed slightly in movement. Consequently, the IDM has been widely used to describe intelligent vehicles. Most of the micro-simulation-based studies developed adaptive cruise control (ACC), cooperative adaptive cruise control (CACC), automated vehicle (AV), or CAVs car-following models of intelligent vehicles based on the IDM and the MIXIC [39]. Exiting IDM based controller can be classified as extended multi-anticipative forward-looking CF models [40, 41] or other modified IDM which have similar structure to IDM [42, 43]. For the extended models that contain IFT, researchers considered the characteristics of drivers or multi-anticipate preceding vehicles to extend IDM, and investigate the stability conditions based on it.
In previous studies, many models based on bidirectional IFT have been proposed. These extended structures are found that they can improve the stability of the string compared with the original model. However, the disadvantage in most of the exit models is that the information item has not been integrated into the model as a specific physical meaning term. Information items in most of models are expressed as the original model multiplied by the coefficient. The target vehicle optimization equation is represented by the original model, and the new model is the combination of the information item and the target vehicle optimization equation. Actually, the form of original model is not changed, and the change is the coefficient of original model.
In this paper, the extended model is not the coefficient changed IDM, and the information of preceding and following vehicles is integrated into the model as the specific meaning term to optimize the acceleration of the target vehicle. The improvement effect of string stability under the bidirectional IFT structure, provides a reference for controller designing. The aim of stability analysis is to investigate how does the perturbation evolve by assuming vehicles travel on a single lane in a platoon [44]. The string stability analysis methods can be classified into three categories: the direct transfer function based method, the Laplace transform based method, and the characteristic equation based method [45].
This paper proposes an extended back-looking car-following model based on the IDM for vehicles in CAVs environment, considering the desired distance of the following vehicle as a control term, which is called intelligent back-looking distance driver model (IBDM) in the following paper. Then, the string stability of the proposed model is investigated by using Laplace transform based method.
The rest of paper is organized as follows: Section 2 presents the IBDM. In Section 3, the linear stability condition is derived using the Laplace transform based method. Section 4 conducts the numerical simulation to verify the linear stability condition. Section 5 presents the conclusion.
2 Intelligent back-looking distance driver model
The intelligent driver model (IDM) was proposed by TREIBER et al [6]. It takes into account the velocity difference to describe the behavior of individual vehicles and enable to play an essential stabilizing role in real traffic, especially in avoiding rear-end collisions. The acceleration of the n-th vehicle at time t is determined by the current velocity vn(t), the headway sn(t), and the velocity difference (approaching rate) Δvn(t) to the preceding vehicle, which can be expressed as:
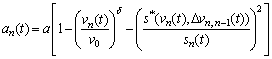 (1)
(1)
 (2)
(2)
where a is the maximum acceleration of the vehicle; v0 is the desired velocity in free flow; δ is the acceleration exponent; s*(t) is the desired distance; s0 is the minimum space distance between two adjacent vehicles in a fully congested traffic situation; Tn is the constant desired time headway between two adjacent vehicles; b is the desired deceleration. It can be observed from Eq. (2) that the last term can only work in a non-stationary situation with the velocity difference between two adjacent vehicles not equal to 0, that is 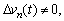 and the braking deceleration is limited to b. The original IDM model can be divided into two parts, namely the acceleration strategy in a free flow state:
and the braking deceleration is limited to b. The original IDM model can be divided into two parts, namely the acceleration strategy in a free flow state:
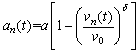 (3)
(3)
and the deceleration strategy when braking is as follows:
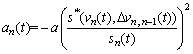 (4)
(4)
When the vehicles connected with each other, the drivers could know the information of the front and rear vehicles. Thus, the acceleration of the individual vehicle could adjust to improve the driver’s behavior, and enhance the stability of the platoon. In this article, it takes into account the desired distance of the following vehicle to optimize vehicle’s acceleration. The mathematical expression of the IBDM is as follows:
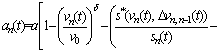
 (5)
(5)
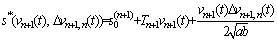 (6)
(6)
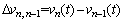 (7)
(7)
where the parameter γ is the weight of the desired distance of the following vehicle; 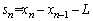 is the net gap between vehicle n and preceding vehicle n-1; L is the average vehicle length;
is the net gap between vehicle n and preceding vehicle n-1; L is the average vehicle length;  is the velocity difference.
is the velocity difference.
3 Linear stability analysis
In this section, the linear stability method is applied for the IBDM described by Eqs. (5)-(7). The steady state of the proposed model has the same homogeneous flow solution, namely:
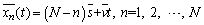 (8)
(8)
where 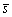 is the average headway of adjacent vehicles in the homogeneous traffic flow;
is the average headway of adjacent vehicles in the homogeneous traffic flow;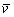 is the velocity of vehicles in the homogeneous traffic flow;
is the velocity of vehicles in the homogeneous traffic flow; 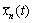 is the location of the vehicle n at time t. All of the variables have a definite value in the initial state, and all vehicles run with the same headway and velocity as well.
is the location of the vehicle n at time t. All of the variables have a definite value in the initial state, and all vehicles run with the same headway and velocity as well.
Let yn(t) be a small perturbation with linear Fourier-mode expanding from the steady state position of the vehicle n at time t. The form is as follows:
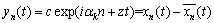
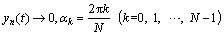 (9)
(9)
where c is a constant.
The second derivative of both sides of Eq. (9) can be conducted:
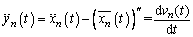 (10)
(10)
Eq. (10) can be written as:
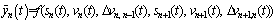 (11)
(11)
Linearizing Eq. (11), the following equation can be obtained:

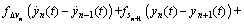
 (12)
(12)
where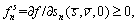

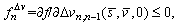 Eq. (12) can be written as the following difference equation:
Eq. (12) can be written as the following difference equation:
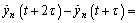
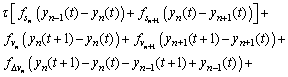
 (13)
(13)
Then the algebraic equation for z can be obtained for any mode of perturbation (k = 0, 1, …, n-1). Substituting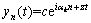 and
and 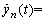
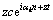 into Eq. (13), the resulted equation is as follows:
into Eq. (13), the resulted equation is as follows:
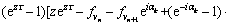
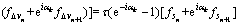 (14)
(14)
Expanding

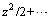 and inserting into Eq. (14), then the first order and second-order terms of coefficients of the expression of z are given respectively as follows:
and inserting into Eq. (14), then the first order and second-order terms of coefficients of the expression of z are given respectively as follows:
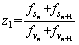 (15)
(15)
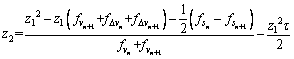 (16)
(16)
The stationary traffic flow is stable if z2>0 for small disturbances with long wavelengths, so the traffic reaches steady-state when the following condition is satisfied:
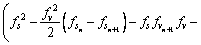
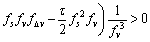 (17)
(17)
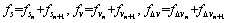 (18)
(18)
The homogeneous traffic flow is stable if Eq. (17) is satisfied. Under the situation, all vehicles have the same velocity. As a consequence, the acceleration and velocity difference are zero for all vehicles, that is a=0, △v=0. The balanced state equation is as follows:
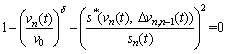 (19)
(19)
where the value of δ is set as 4 [6] and other parameters of the model are listed in Table 1.
The specific forms of fsn, fsn+1, fvn, fvn+1, f△vn, f△vn+1 can be conducted as follows:
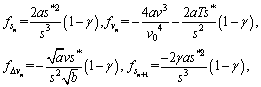
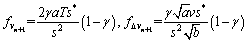 (20)
(20)
Table 1 Parameter values of IDM [6, 46]

Inserting Eqs. (18) and (20) into Eq. (17), the condition of a stable state can be solved.
The homogeneous traffic flow satisfies 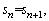
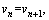
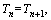
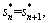
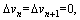 consequently. Equation (17) can be simplified as:
consequently. Equation (17) can be simplified as:
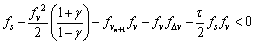 (21)
(21)
When γ=0, the IBDM degenerates to the IDM and fvn+1=0. The stable condition of IDM is as follows:
 (22)
(22)
The neutral stability curves can be obtained from Eq. (21). Figure 1 shows the neutral stability curves in different velocity with the change of parameter γ when τ=0.1 (the original IDM does not contain the reaction time, so as the IBDM). Moreover, other parameters are set as shown in Table 1. Stability lines are critical boundaries of the stable and unstable region. The traffic flow is stable when the desired time gap in the above of the stability line with correspondent velocity, vice versa. In some articles, the headway of CAV vehicle is smaller than that in human driving [47, 48]. However, in order to compare the influence of bidirectional IFT, all parameters are taken as the same value, which is convenient for comparison.
In Figure 1, the dotted line represents the stability region of the IDM. When γ=0, the IBDM degenerates to the IDM. Solid lines represent the stability region of IBDM with different values of γ. The sign of γ represents positive or negative influence for vehicle’s acceleration that the desired distance of the following vehicle brings. The absolute value of γ represents the influence degree of the following vehicle. From Figure 1, it can be observed that the stability line becomes higher than the IDM when γ>0; otherwise, the stability line becomes lower than the IDM. It means that taking into account the desired distance of the following vehicle would reduce the vehicle’s acceleration, and improve the string stability. In the real world, it expresses as the vehicle accelerate more gentle, for accounting the movement of vehicle following. When γ<0, the stability line becomes lower with the decrease of γ (the absolute value of γ increase), and the stable region increases. It means that the string stability of IBDM improves with an increase of concerning the degree of the following vehicle.
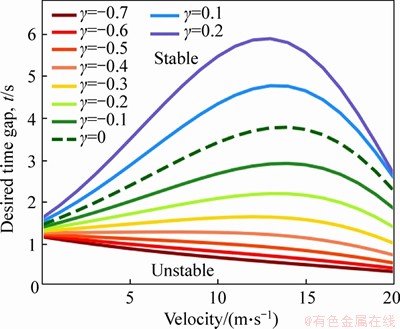
Figure 1 Neutral stability curves with change of γ when τ=0.1
To verify the result, we implement simulation in six scenarios in the next part. Because these extended models are based on different CF models in which calibration parameters are different, the effect of the proposed model can be distinguished only by comparing with the same extended IDM that has the same calibration parameters. In this paper, the original IDM and the extended model considering the front vehicle and the next adjacent front vehicle proposed by LI et al [40] are selected to compare the difference between the bidirectional IFT and the one-way IFT. The information of IBDM comes from the near preceding vehicle and near following vehicle, while the information of Li’s model comes from the near preceding vehicle and next near preceding vehicle. Both of the IBDM and Li’s model (L-IDM) considered two information flow. L-IDM is as follows:
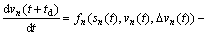
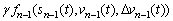 (23)
(23)
where fn is the information of the preceding vehicle (IDM); fn-1 is the information of the near-preceding vehicle.
4 Simulation
A 101-vehicle platoon was simulated in MATLAB, running on a single lane, with the open boundary condition. All of the vehicles are in the same initial condition where they have the same initial velocity, the same space distance between adjacent vehicles, and the same control model except the tail vehicle, which does not have the following vehicle in a platoon. The simulation lasted for 350 s. Parameters of the IDM are shown in Table 1. To compare the string stability of the model in the same condition, the parameters of the IBDM are set as the same in comparison.
When a vehicle merges or cuts into the head of the platoon, the disturbance maybe occurs the first vehicle of the platoon. It reflects the sudden acceleration changes of the first vehicle, so is the vehicle in the middle of platoon when a vehicle merges or cuts in into the middle of the platoon. As a result, the simulation of the six scenarios in the paper is the abstract of these situations, simulating the cases that the disturbance occurred in the first or the middle platoon. For convenient to observe the string stability of the platoon and compare among these six scenarios, these disturbances are unified as small disturbances.
The traffic disturbance is induced by leading vehicle suddenly decelerated at a moment with a specific deceleration, and then kept constant. The respond of the following vehicles has been investigated with different combinations of the coefficients of initial conditions. Six scenarios are displayed in Table 2, with the combinations of the coefficients. The different parameters, γ=0.1, γ=0, γ=-0.2, γ=-0.3, γ=-0.6, were simulated in these scenarios.
Scenario 1 is to investigate the effect of γ. Scenarios 2 and 3 investigate the changes of stability condition with the initial velocity and reaction time. Scenario 4 is to investigate the influence of the disturbance. Scenario 5 is to investigate the influence of the space distance. Scenario 6 is to investigate the influence of the disturbance vehicle.
The results of scenario 1 are shown in Figures 2 and 3. Figure 2 shows the acceleration changes of the platoon when γ=0.1, γ=0, γ=-0.2, γ=-0.6. It can be seen in Figures 2(a)-(c) that the overall shape of the acceleration curve is diffusive, which means that the acceleration curves of vehicles fluctuate through time. And the fluctuation is more serious when the vehicle nears the tail of platoon. It reveals that the small disturbance propagates and amplifies along with the platoon, and the traffic flow is unstable in all of three cases. However, it can be found that the degree of amplification decreases with the decrease of γ, which means that the stability is improved with the decrease of γ. When γ descends to -0.6, the traffic flow is stable, as shown in Figure 2(d). Thus the string stability can be improved with the decrease of γ in the IBDM. To observe the rule more clearly, Figure 2(d) displays the acceleration curves of four vehicles along with the platoon. In the case, the acceleration curve is convergence to a certain extent, and the fluctuation degree reduces along with the platoon, which can be seen in Figure 3. Figure 2(e) shows the acceleration changes of the platoon in scenario 1 when γ=-0.6 in L-IDM. It can be seen that the disturbance got smaller through the platoon, but is larger than that in Figure 2(d). So the ability to eliminate the disturbance of IBDM is better in that case.
Table 2 Parameter values of six scenarios
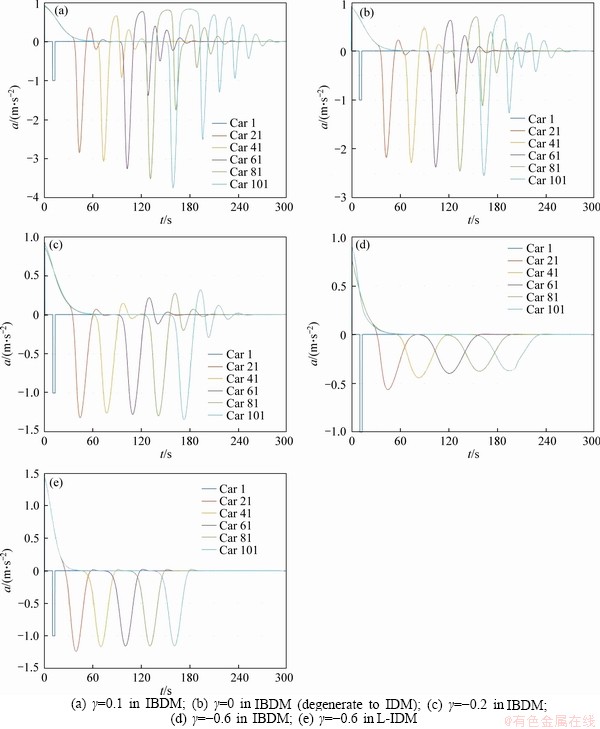
Figure 2 Acceleration changes of platoon in scenario 1:
Figure 3 displays the acceleration and velocity changes through the simulation time for the 1st vehicle, the 25th vehicle, the 50th vehicle and the 100th vehicle in the platoon, for γ=0, γ=-0.6. It can be seen in Figure 3 that the small disturbance of acceleration propagated and amplifies along with the platoon when γ=0, and the velocity lines fluctuate as well. However, the acceleration and velocity lines are converged when γ=-0.6. It means that the traffic flow is stable when γ=-0.6 and unstable when γ=0. It is consistent with the neutral stability curves and the string stability has been improved with the decrease of γ in the IBDM.
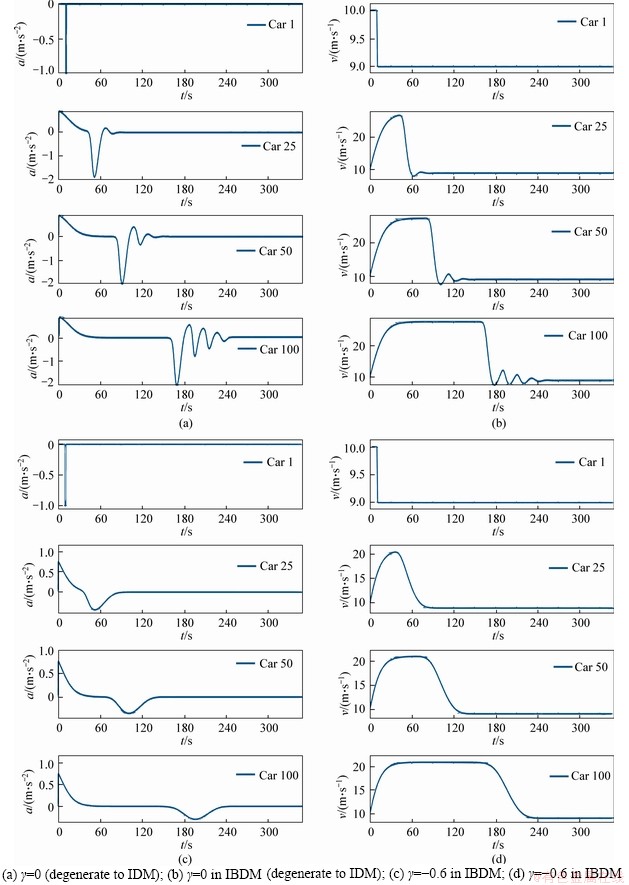
Figure 3 Time series diagram of acceleration and velocity in IBDM:
Figure 4 shows the position changes of the platoon when γ=0, γ=-0.6, respectively. The traffic flow is unstable when γ=0, and the traffic flow is stable when γ=-0.6. Compared with Figure 4(b), the shock wave appears in Figure 4(a), and the tail position is more forward at the same time. It means that the platoon sacrifices the desire to close to the front vehicle as much as possible to improve the stability but considering the condition of the rear vehicles. In that case, the movement of vehicles in platoon cooperates with each other to avoid accelerating and decelerating frequently. Hence, their acceleration changes are more gently.
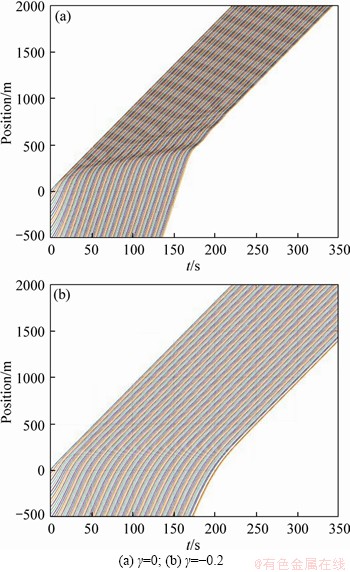
Figure 4 Position changes of platoon in scenario 1 in IBDM:
Figure 5 shows the case when γ=0, γ=-0.2 in the IBDM in scenario 2, and in the L-IDM when γ=-0.2 in scenario 2. Figures 5(a) and (b) show the unstable case and stable case in the IBDM, respectively. The result is consistent with the neutral stability analysis. And the stable state in Figure 5(b) is better than that in Figure 5(c).
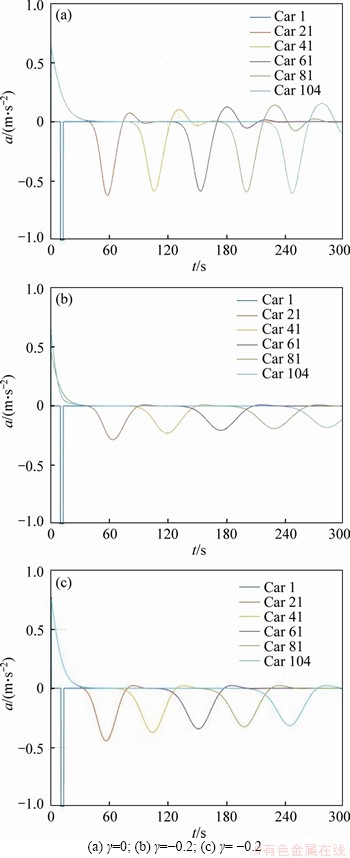
Figure 5 Acceleration changes of platoon in scenario 2:
Scenarios 3-6 in the IBDM are shown in Figures 6(a)-(d), respectively. It is found that all of the cases are stable. Figures 2(d) and 6(b) reveal that different small disturbances do not affect the stability condition. Together with Figures 6(c) and 6(d), the result illustrates that the initial space distance and different location of small disturbance do affect the stability condition, that is, the tendency to equilibrium would not change. The only difference between these cases is the level of acceleration for each vehicle.
Figure 7 shows the cases in the L-IDM corresponding to that in Figure 6. It can be seen, all of the cases are stable in L-IDM, but the disturbance is bigger than that in IBDM. It reveals that the IBDM has better ability to eliminate the disturbance.
The result above shows that under the specific condition where the IDM could bring the instability of the traffic flow, using the proposed model could diminish the disturbance by increasing the parameter related to the desired space of the following vehicle. The impact of the desired distance of vehicle following is presented as γ. Neutral stability curves show that the stable region extends with a decrease of γ. If γ=0, the IBDM degenerates to the IDM, representing the case where vehicles run without considering the desired distance of the following vehicle. If γ≠0, vehicles consider the desired distance of the following one. The sign of γ means the positive or negative impact of the new term of the acceleration. When γ>0, the traffic stability is worse than the IDM, and when γ<0, the traffic stability is better than the IDM. It means that the acceleration of the target vehicle decreases with considering the following vehicle, to improve the traffic stability. When γ<0, the traffic stability improves with the decrease of γ, which means that the stability improves by increasing the proportion of the following term. Under the different disturbance strength, disturbance location, and initial platoon space distance, the tendency to equilibrium does not change.
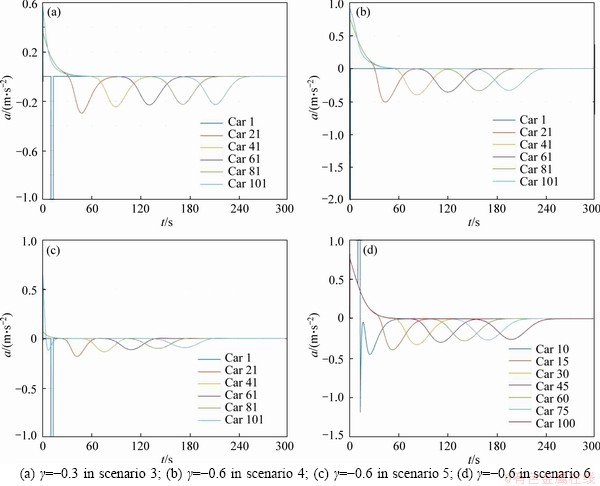
Figure 6 Acceleration changes of platoon in IBDM:
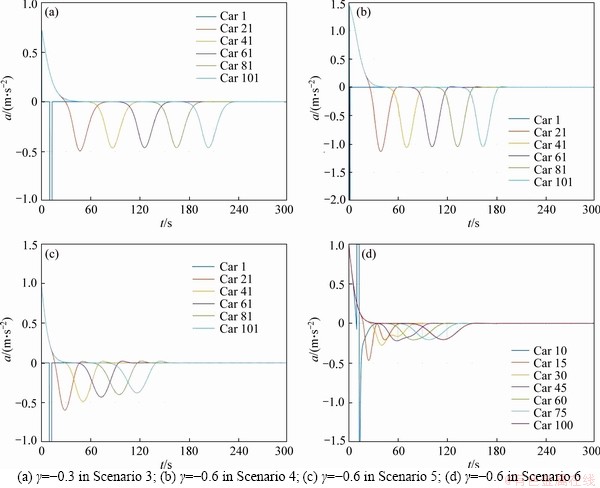
Figure 7 Acceleration changes of platoon in scenarios 3-6 in L-IDM:
In the IDM, vehicles only consider the information in front and drivers depend on the moving of the preceding vehicle to make decisions. However, for the IBDM, vehicles could receive information about the preceding and the following vehicle. When a disturbance appeared, they could coordinate with each other by considering the following vehicle, reducing the frequency of acceleration and deceleration. As a result, the IBDM has better performance in maintaining the string stability of the platoon than IDM and L-IDM, and the simulations verified the conclusion. Moreover, with the comparison of L-IDM, both of two models improve the string stability of traffic flow, but the IBDM has better performance. The result reveals that the model considering the information of vehicle preceding and following has better performance than the model considering the information of vehicle preceding and next preceding. In addition, this model can be used in the condition of the CAVs environment, where the technology could enhance the driver’s ability to evaluate the conditions behind.
This paper considers the linear stability of platoon, abstract the disturbances generated by merging, cutting in and other operations, and investigates the ability to resist small disturbances of traffic flow. As a result, the simulations of the six scenarios in the paper are the abstract of these situations, showing the cases where the disturbance occurred in the first or the middle platoon. However, in the real world, the case may not be that simple. These disturbances will be more complicated or may be the combination of several facts to form a complicated situation. Consequently, the effectiveness of the proposed model should be tested and verified in real world in the future.
5 Conclusions
This paper proposed an intelligent back- looking distance driver model in CAVs environment, considering the desired distance of the following vehicle, and investigated the linear stability effect for the traffic. The stability condition against a small perturbation is analyzed using linear stability theory. Then, simulations were conducted to investigate the stability of the proposed model and compare it with the IDM and the extended IDM considering the nearest preceding vehicle. Six scenarios are designed to evaluate the result under different disturbance strength, disturbance location, and initial platoon space distance. The range and effect of the parameter that represents the proportion of desired distance were discussed and concluded. And the simulation result is consistent with the neutral stability analysis. And the IBDM has better performance than the extended IDM considering the information of the preceding vehicle and next preceding vehicle.
The theoretical and simulation results indicate that the IBDM improves the string stability compared with the IDM, and the stability can be improved by increasing the proportion of the desired distance of the following vehicle. When a disturbance appeared, vehicles in platoon coordinate with each other by considering the preceding vehicle and following vehicle, diminishing the disturbance by reducing acceleration/deceleration frequently. Thus, the string stability of traffic is improved.
Moreover, in this work, the homogeneous traffic flow was investigated, and the simulation was carried out in the homogeneous initial conditions. More work should be done in heterogeneity situations in the future as follows: 1) In heterogeneity traffic flow, in which vehicles do not obey the same car-following model; 2) Simulations on heterogeneity initial conditions, investigating the effectiveness of the IBDM in the complicated environment; 3) Real world testing should be done to investigate the effect of model.
Contributors
The overarching research goals were developed by YI Zi-wei, LU Wen-qi, XU Ling-hui, QU Xu, RAN Bin. YI Zi-wei and LU Wen-qi established the models and derived the stability formulas. YI Zi-wei and XU Ling-hui conducted the simulation and drew the figures. YI Zi-wei, QU Xu and RAN Bin analyzed the results. The initial draft of the manuscript was written by YI Zi-wei. LU Wen-qi and XU Ling-hui revised the manuscript. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
YI Zi-wei, LU Wen-qi, XU Ling-hui, QU Xu, RAN Bin declare that they have no conflict of interest.
References
[1] PIPES L A. An operational analysis of traffic dynamics [J]. Journal of Applied Physics, 1953, 24(3): 274-281. DOI: 10.1159/000191390.
[2] NEWELL G F. Mathematical models for freely-flowing highway traffic [J]. Journal of the Operations Research Society of America, 1955, 3(2): 176-186. DOI: 10.1287/ opre.3.2.176.
[3] CHANDLER R E, HERMAN R, MONTROLL E W. Traffic dynamics: Studies in car following [J]. Operations Research, 1958, 6(2): 165-184. DOI: 10.1287/opre.6.2.165.
[4] GIPPS P G. A behavioural car-following model for computer simulation [J]. Transportation Research Part B: Methodological, 1981, 15(2): 105-111. DOI: 10.1016/ 0191-2615(81)90037-0.
[5] BANDO M, HASEBE K, NAKAYAMA A, SHIBATA A, SUGIYAMA Y. Dynamical model of traffic congestion and numerical simulation [J]. Physical Review E, 1995, 51(2): 1035-1042. DOI: 10.1103/PhysRevE.51.1035.
[6] TREIBER M, HENNECKE A, HELBING D. Congested traffic states in empirical observations and microscopic simulations [J]. Physical Review E, 2000, 62(2): 1805-1824. DOI: 10.1103/PhysRevE.62.1805.
[7] JIANG R, WU Q, ZHU Z. Full velocity difference model for a car-following theory [J]. Physical Review E-Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2001, 64(1): 017101. DOI: 10.1103/PhysRevE.64. 017101.
[8] QU Xu, YANG Mo-feng, YANG Fan, RAN Bin, LI Lin-chao. An improved single-lane cellular automaton model considering driver's radical feature [J]. Journal of Advanced Transportation, 2018: 3791820. DOI: 10.1155/2018/ 3791820.
[9] LI Lin-heng, GAN Jing, WU Xu, MAO Pei-pei, RAN Bin. Car-following model based on safety potential field theory under connected and automated vehicle environment [J]. China Journal of Highway and Transport, 2019, 32(12): 76-87. DOI: 10.1017/CBO9781107415324.004. (in Chinese)
[10] WONG W, SHEN S Y, ZHAO Y, LIU H X. On the estimation of connected vehicle penetration rate based on single-source connected vehicle data [J]. Transportation Research Part B: Methodological, 2019, 126: 169-191. DOI: 10.1016/j.trb.2019.06.003.
[11] LI Lin-heng, GAN Jing, LI Wen-quan. A separation strategy for connected and automated vehicles: utilizing traffic light information for reducing idling at red lights and improving fuel economy [J]. Journal of Advanced Transportation, 2018: 5679064. DOI: 10.1155/2018/5679064.
[12] LI Lin-chao, DU Bo-wen, WANG Yong-gang, QIN Ling-qiao, TAN Hua-chun. Estimation of missing values in heterogeneous traffic data: Application of multimodal deep learning model [J]. Knowledge-Based Systems, 2020, 194: 105592. DOI: 10.1016/j.knosys.2020.105592.
[13] ZHENG Yuan, ZHANG Yu, RAN Bin, XU Yue-ru, QU Xu. Cooperative control strategies to stabilize the freeway mixed traffic stability and improve traffic throughput in an intelligent roadside system environment [J]. IET Intelligent Transport Systems, 2020, 14(9): 1108-1115. DOI: 10.1049/iet-its.2019.0577.
[14] GONG Si-yuan, ZHOU An-ye, PEETA S. Cooperative adaptive cruise control for a platoon of connected and autonomous vehicles considering dynamic information flow topology [J]. Transportation Research Record: Journal of the Transportation Research Board, 2019, 2673(10): 185-198. DOI: 10.1177/0361198119847473.
[15] MOSER D, SCHMIED R, WASCHL H, DEL RE L. Flexible spacing adaptive cruise control using stochastic model predictive control [J]. IEEE Transactions on Control Systems Technology, 2018, 26(1): 114-127. DOI: 10.1109/TCST. 2017.2658193.
[16] XIAO Lin, WANG Meng, van AREM B. Realistic car-following models for microscopic simulation of adaptive and cooperative adaptive cruise control vehicles [J]. Transportation Research Record: Journal of the Transportation Research Board, 2017, 2623(1): 1-9. DOI: 10.3141/2623-01.
[17] ZHENG Yang, LI S E, LI Ke-qiang, WANG Le-yi. Stability margin improvement of vehicular platoon considering undirected topology and asymmetric control [J]. IEEE Transactions on Control Systems Technology, 2016, 24(4): 1253-1265. DOI: 10.1109/TCST.2015.2483564.
[18] AL-JHAYYISH A M H, SCHMIDT K W. Feedforward strategies for cooperative adaptive cruise control in heterogeneous vehicle strings [J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(1): 113-122.
[19] WANG Chao-jie, GONG Si-yuan, ZHOU A, LI T, PEETA S. Cooperative adaptive cruise control for connected autonomous vehicles by factoring communication-related constraints [J]. Transportation Research Procedia, 2019, 38: 242-262. DOI: 10.1016/j.trc.2019.04.010.
[20] QI Xin-yue, GE Hong-xia, CHENG Rong-jun. Analysis of a novel lattice hydrodynamic model considering density integral and “backward looking” effect [J]. Physica A: Statistical Mechanics and its Applications, 2019, 525: 714-723. DOI: 10.1016/j.physa.2019.03.030.
[21] WANG Qing-ying, GE Hong-xia. An improved lattice hydrodynamic model accounting for the effect of “backward looking” and flow integral [J]. Physica A: Statistical Mechanics and its Applications, 2019, 513: 438-446. DOI: 10.1016/j.physa.2018.09.025.
[22] WANG Zi-hao, GE Hong-xia, CHENG Rong-jun. Nonlinear analysis for a modified continuum model considering driver's memory and backward looking effect [J]. Physica A: Statistical Mechanics and its Applications, 2018, 508: 18-27. DOI: 10.1016/j.physa.2018.05.072.
[23] JIAO Yu-lei, GE Hong-xia, CHENG Rong-jun. Nonlinear analysis for a modified continuum model considering electronic throttle (ET) and backward looking effect [J]. Physica A: Statistical Mechanics and its Applications, 2019, 535: 122362. DOI: 10.1016/j.physa.2019.122362.
[24] ZHAI Cong, WU Wei-tiao. Analysis of drivers’ characteristics on continuum model with traffic jerk effect [J]. Physics Letters A, 2018, 382(47): 3381-3392. DOI: 10.1016/ j.physleta.2018.09.029.
[25] WANG Ju-feng, SUN Feng-xin, GE Hong-xia. Effect of the driver’s desire for smooth driving on the car-following model [J]. Physica A: Statistical Mechanics and Its Applications, 2018, 512: 96-108. DOI: 10.1016/j.physa.2018.08.025.
[26] LI Teng-long, HUI Fei, ZHAO Xiang-mo. An improved car-following model considering the impact of safety messages [J]. Modern Physics Letters B, 2018, 32(32): 1850398. DOI: 10.1142/s0217984918503980.
[27] KESTING A, TREIBER M, HELBING D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2010, 368(1928): 4585-4605. DOI: 10.1098/rsta.2010.0084.
[28] DAVIS L C. Effect of adaptive cruise control systems on traffic flow [J]. Physical Review E, 2004, 69(6): 066110. DOI: 10.1103/PhysRevE.69.066110.
[29] HERMAN R, MONTROLL E W, POTTS R B, ROTHERY R W. Traffic dynamics: analysis of stability in car following [J]. Operations Research, 1959, 7(1): 86-106. DOI: 10.1287/opre.7.1.86.
[30] NAKAYAMA A, SUGIYAMA Y, HASEBE K. Effect of looking at the car that follows in an optimal velocity model of traffic flow [J]. Physical Review E-Statistical, Nonlinear, and Soft Matter Physics, 2002, 65(1, 2): 016112. DOI: 10.1103/PhysRevE.65.016112.
[31] HASEBE K, NAKAYAMA A, SUGIYAMA Y. Dynamical model of a cooperative driving system for freeway traffic [J]. Physical Review E-Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2003, 68(2): 026102. DOI: 10.1103/PhysRevE.68.026102.
[32] GE H X, ZHU H B, DAI S Q. Effect of looking backward on traffic flow in a cooperative driving car following model [J]. The European Physical Journal B, 2006, 54(4): 503-507. DOI: 10.1140/epjb/e2007-00014-x.
[33] SUN Di-hua, LIAO Xiao-yong, PENG Guang-han. Effect of looking backward on traffic flow in an extended multiple car-following model [J]. Physica A: Statistical Mechanics and its Applications, 2011, 390(4): 631-635. DOI: 10.1016/j.physa.2010.10.016.
[34] YANG Shu-hong, LIU Wei-ning, SUN Di-hua, LI Chun-gui. A new extended multiple car-following model considering the backward-looking effect on traffic flow [J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(1): 011016. DOI:10.1115/1.4007310.
[35] YANG Da, JIN P, PU Yun, RAN Bin. Safe distance car-following model including backward-looking and its stability analysis [J]. The European Physical Journal B, 2013, 86(3): 92. DOI: 10.1140/epjb/e2012-30688-6.
[36] HOU Pei-guo, YU Han-wei, YAN Chen, HONG Jia-yang. An extended car-following model based on visual angle and backward looking effect [J]. Chinese Journal of Physics, 2017, 55(5): 2092-2099. DOI: 10.1016/j.cjph.2017.08.027.
[37] CHEN Can, CHENG Rong-jun, GE Hong-xia. An extended car-following model considering driver’s sensory memory and the backward looking effect [J]. Physica A: Statistical Mechanics and its Applications, 2019, 525: 278-289. DOI: 10.1016/j.physa.2019.03.099.
[38] MA Guang-yi, MA Ming-hui, LIANG Shi-dong, WANG Yan-song, ZHANG Yao-zong. An improved car-following model accounting for the time-delayed velocity difference and backward looking effect [J]. Communications in Nonlinear Science and Numerical Simulation, 2020, 85: 105221. DOI: 10.1016/j.cnsns.2020.105221.
[39] DO W, ROUHANI O M, MIRANDA-MORENO L. Simulation-based connected and automated vehicle models on highway sections: A literature review [J]. Journal of Advanced Transportation, 2019: 9343705. DOI: 10.1155/2019/9343705.
[40] LI Zhi-peng, LI Wen-zhong, XU Shang-zhi, QIAN Ye-qing. Stability analysis of an extended intelligent driver model and its simulations under open boundary condition [J]. Physica A: Statistical Mechanics and its Applications, 2015, 419: 526-536. DOI: 10.1016/j.physa.2014.10.063.
[41] CHEN X, LI R, XIE W, SHI Q. Stabilization of traffic flow based on multi-anticipative intelligent driver model [C]// 2009 12th International IEEE Conference on Intelligent Transportation Systems. St Louis: IEEE, 2009: 72–77. DOI: 10.1109/ITSC.2009. 5309847.
[42] LU Chao-ru, AAKRE A. A new adaptive cruise control strategy and its stabilization effect on traffic flow [J]. European Transport Research Review, 2018, 10(2): 1-11. DOI: 10.1186/s12544-018-0321-9.
[43] LU Chao-ru, DONG Jing, HU Liang, LIU Chen-hui. An ecological adaptive cruise control for mixed traffic and its stabilization effect [J]. IEEE Access, 2019, 7: 81246-81256. DOI: 10.1109/ACCESS.2019.2923741.
[44] GU H, ZHANG J, JIN P J, RAN B. Stability analysis of lead-vehicle control model in cooperative adaptive cruise control platoon within heterogeneous traffic flow [J]. Journal of Southeast University, 2018, 34 (3): 386-393. DOI: 10.3969/j.issn.1003-7985.2018.03.015. (in Chinese)
[45] SUN Jie, ZHENG Zu-duo, SUN Jian. Stability analysis methods and their applicability to car-following models in conventional and connected environments [J]. Transportation Research Part B: Methodological, 2018, 109: 212-237. DOI: 10.1016/j.trb.2018.01.013.
[46] KESTING A, TREIBER M, SCHONHOF M, KRANKE F, HELBING D. Jam-avoiding adaptive cruise control (ACC) and its impact on traffic dynamics [J]. Traffic and Granular Flow’05, 2007: 633-643. DOI: 10.1007/978-3-540-47641- 2_62.
[47] MILANES V, SHLADOVER S E, SPRING J, NOWAKOWSKI C, KAWAZOE H, NAKAMURA M. Cooperative adaptive cruise control in real traffic situations [J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 296-305. DOI: 10.1109/TITS.2013.2278494.
[48] MILANES V, SHLADOVER S E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data [J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 285-300. DOI: 10.1016/ j.trc.2014.09.001.
(Edited by ZHENG Yu-tong)
中文导读
考虑回望距离的智能网联自动驾驶车辆智能驾驶模型及其稳定性
摘要:在汽车跟驰(CF)过程中,智能网联自动驾驶技术为驾驶员提供了更多的信息。与人类驾驶车辆(HVs)只考虑前方信息不同,智能网联自动驾驶车辆(CAVs)能够获取前方和后方的信息,增强了车辆的感知能力。本文提出了一种考虑回望距离的智能驾驶模型(IBDM),考虑了CAVs环境下车辆跟驰行驶时相对于前后车的期望距离。基于智能驾驶模型(IDM),IBDM将车辆后方信息作为控制项集成进模型中。利用线性稳定性原理和李雅普诺夫稳定性分析方法,分析了均质交通流中在小扰动下的稳定性条件。为了验证理论分析的正确性,在开放边界条件下,在单车道上进行了仿真,并与不考虑后车的IDM和考虑前后车信息的扩展IDM进行了比较。设计了六种方案,对不同干扰强度、干扰位置和初始队列间距下的结果进行评估。结果表明,IBDM在控制CAVs跟驰过程中保持弦稳定性方面优于IDM和扩展IDM,并通过增加考虑前车的比重来提高稳定性。
关键词:线性稳定性;智能驾驶模型;智能网联自动驾驶车辆
Foundation item: Project(2018YFB1600600) supported by the National Key Research and Development Program, China; Project(20YJAZH083) supported by the Ministry of Education, China; Project(20YJAZH083) supported by the Humanities and Social Sciences, China; Project(51878161) supported by the National Natural Science Foundation of China
Received date: 2020-03-09; Accepted date: 2020-07-22
Corresponding author: QU Xu, PhD, Associate Professor; Tel: +86-13584010880; E-mail: quxu@seu.edu.cn; ORCID: https://orcid.org/ 0000-0003-3256-8920

