­­Thermal residual stress of polycrystalline diamond compacts

CHEN Feng(陈 枫)¹, XU Gen(徐 根)², MA Chun-de(马春德)¹, XU Guo-ping(徐国平)³

1. Testing Center, Central South University, Changsha 410083, China;

2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

3. King-ray New Materials Science & Technology Co., Ltd., Changsha 410012, China

Received 22 December 2008; accepted 7 April 2009

Abstract: Thermal residual stresses in polycrystalline diamond compact (PDC) cutter arising from the difference in thermal expansion between the polycrystalline diamond (PCD) and the supporting tungsten carbide substrate after sintering at high pressure and high temperature were investigated using finite element simulation, laboratory tests and theoretical analysis. The obtained results show that although compressive residual stresses exist both in the interface of PCD table and in the most region of PCD table surface, the tensile residual stress, which is a fatal shortage to PDC, can also occur near the outer diameter area of PCD table, and the maximum value is 690 MPa. Distribution of tensile stress in the PCD table is given through experimental results, which is well consistent with the numerical results. This finding may be significant in designing new PDC cutters with lower residual stress and high cutting behavior.

Key words: polycrystalline diamond compact; diamond; thermal residual stress; stress release

1 Introduction

Polycrystalline diamond compact (PDC), consisting of a polycrystalline diamond (PCD)-Co layer on a WC-Co substrate, is extensively used to drill oil and gas wells[1-3]. Commercially available diamond compacts are usually made by sintering diamond powders in the temperature range from 1 400 ℃ to 2 000 ℃ at pressure of 5-7 GPa by using suitable metallic solvent catalysts, such as iron, nickel and manganese. In the present investigation, sintering temperature and pressure are    1 450 ℃ and 5.5 GPa, respectively[4].

However, two severe issues may occur in the sintering process of PDC. Firstly, the mismatch of thermal expansion coefficients between diamond and catalyst metal may induce significant internal stress, which may generate micro-cracks within the polycrystalline diamond layer. This will greatly reduce the resistance of the cutting element to mechanical or thermal shock[5-6]. And secondly, the different thermal expansion of the polycrystalline diamond layer and the tungsten carbide substrate may also result in significant residual stresses in the PDC cutter upon cooling from the sintering temperature to room temperature[7]. Especially, the tensile thermal residual stresses in PCD table are the most harmful to PDC cutter, which will cause fracture, delamination and other abnormal failure of PDC cutters [8].

The aim of the present work is to elucidate the distribution features of residual thermal stresses in the interface and diamond table, and to find the relationship between residual stress distribution and failure modes. Finite element simulation, laboratory tests and theoretical analysis are used in the investigation.

2 Thermal residual stress analysis

2.1 Theoretical analysis for thermal residual stress

PDC obtained under high pressure and high temperature, consists of a polycrystalline diamond (PCD) layer and a WC-Co substrate. As pressure is released and the PDC is cooled from the sintering temperature (above 1 100 ℃) to room temperature (20 ℃), the PCD layer and substrate material respond at different rates. A very high thermal residual stresses will be induced in both PCD table and WC-Co substrate due to the mismatch of thermal expansion coefficients between them[9]. Usually, the thermal expansion coefficient of PCD is much lower than that of WC-Co. So, very large compressive stresses are induced in the diamond table, and much little radial tensile stresses are induced in the cemented tungsten carbide substrate. Volumetric strain[10] may provide a clear illustration to the origin of these thermal residual stresses, which can be written as follows:

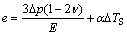                        (1)

where e is the volumetric strain; ?p is the sintering pressure change;  is Poisson ratio; E is the elastic modulus; α is the coefficient of thermal expansion[11]; and ?T_S is the sintering temperature change from the room temperature T to the sintering temperature T_S, which can be expressed as

?T_S=T-T_S                                   (2)

The first term on the right of Eq.(1) denotes the volumetric expansion of PDC material as the pressure is released after sintering. The second term represents the volumetric contraction as the PDC material cools from sintering temperature to room temperature. BERTAQOLLI and VALE[10] suggested a simpler formula to model the combination of both pressure and temperature changes after sintering:

e=α?T_eff                                    (3)

They found a good match between experimental results and numerical calculations of residual stress when ?T_eff=-343 ℃. It can be seen that the negative volumetric strain due to decreasing temperature is more dominant than the positive volumetric strain due to decreasing pressure.

Since the elastic constants, E, and thermal expansion coefficients, α, of diamond material and WC-Co material are quite different, different volumetric subtraction in the same temperature change ?T_eff will induce a huge residual stress in diamond table and tungsten carbide substrate, especially in the interface of two materials. About 70% abnormal failures of PDC cutters, such as diamond and substrate fracture, delamination and chipping or spalling damage are due to thermal residual stresses[12].

2.2 Numerical analysis on residual stress

Thermal residual stress distribution in diamond table can be obtained using three-dimensional finite element analysis(FEA). The material of diamond table used in the present numerical simulation contains 94% diamond and 6% Co (denoted by D6Co), and the substrate contains 15% Co (denoted by YG15). Material constants for both D6Co and YG15 are tested and listed in Table 1. Dimension of the model is shown in Fig.1, with PCD of 1 mm and substrate of 7 mm in thickness.

Table 1 Mechanical constants for diamond table (D6Co) and substrate (YG15)

Fig.1 Geometry of PDC used in numerical simulation

The temperature change used in calculation is from 1 000 ℃ (stress relax point) to 20 ℃ (room temperature) [13]. Elastic constants, E,  and thermal expansion coefficient, α, used in the calculation are listed in Table 1. The calculated radial, axial and shear stresses at different levels AC, DE and OG (Fig.2) are depicted in Fig.3. Fig.4 shows the distribution of thermal residual stresses along y directions.

Fig.2 Local coordinates of diamond table

Fig.3 Thermal residual stress distribution at different levels of PCD: (a) Radial stress; (b) Axial stress; (c) Shear stress

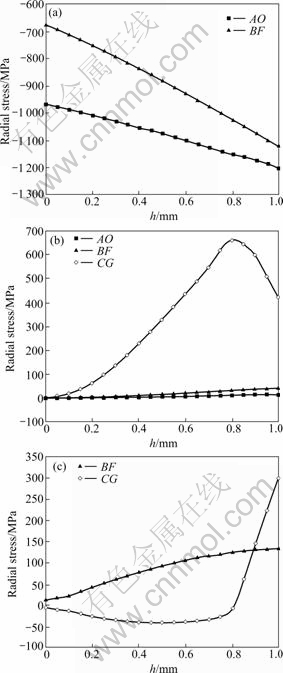
Fig.4 Thermal residual stress distribution along y direction:   (a) Radial stress; (b) Axial stress; (c) Shear stress

Thermal residual stress distributions in both diamond table and substrate are given in Fig.5.

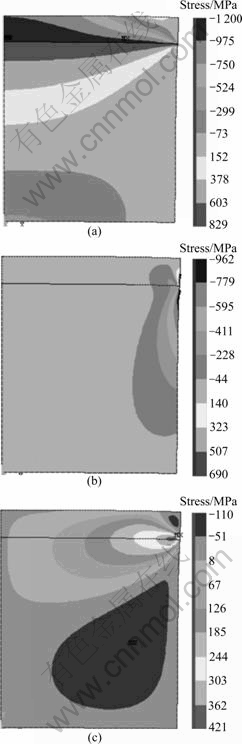
Fig.5 Thermal residual stress distributions in diamond table and substrate: (a) Radial stress distribution; (b) Axial stress distribution; (c) Shear stress distribution

The maximum thermal residual stresses in both diamond table and WC-Co substrate are listed in Table 2.

Table 2 Maximum stresses in PCD table and WC-Co substrate

It can be seen from Figs.3-5 that the maximum stress occurs near the interface. The radial compressive stress in the diamond layer reaches 1.2 GPa, which is near the compressive limit of diamond material (1.9-  6.9 GPa). Both the maximum tensile stress in thickness direction (σ_y) and tensile shear stress between two materials occur in the outer edge of interface. It is potentially very detrimental to the cutter because it makes the cutter more susceptible to gross fracture and delamination at the diamond/carbide interface[14].

2.3 Tests for thermal residual stress using stress release method

In order to investigate the influence of substrate thickness on the thermal residual stress of the diamond table, a procedure called stress release method[15] was applied, and the residual stress on the diamond table surface was measured. Three rosette strain gages were bonded to the diamond table, located at the center, half radius and outer edge of the diamond table, respectively. Four flat interface PDC specimens with the same dimension of d 19 mm×13 mm, but different diamond thickness, 0.5, 1.0, 1.5 and 2.0 mm, were used.

The PDC specimen was then held in a specially designed fixture while the carbide substrate was cut away using electrical discharge wire-cutting machine. The strain gage response can be recorded as a function of substrate thickness. The PCD table is assumed to be stress-free when the substrate material has been removed, thus producing a plot of surface residual stress for each point of the diamond table. The tested results are shown in Table 3.

Table 3 Thermal residual stress at different positions on diamond surface

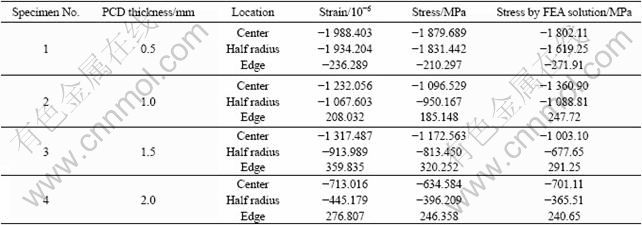
The variation of thermal residual stress with respect to the substrate thickness is shown in Fig.6.

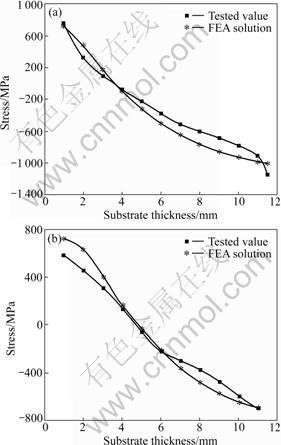
Fig.6 Variation of thermal residual stress with respect to substrate thickness: (a) PCD thickness of 1.5 mm; (b) PCD thickness of 2.0 mm

It can be seen that experimental results correlate well with the calculated ones. Fig.7 shows the radial residual stress distribution along radius of diamond table (for 2 mm-thick diamond table), which can be simulated by the following formula:

              (4)

where σ_r is the radial residual stress (MPa) on PCD surface; and D is the distance (mm) from the calculated point to the center of diamond table.

It can be seen from Fig.7 that the maximum

compressive stress reaches 701.11 MPa at the center of diamond table surface (D=0) while the maximum tensile stress reaches 293.01 MPa at D=8.03 mm. However, it should be pointed out that position of the maximum tensile stress on PCD surface can be changed with the substrate thickness. The experimental results obtained on four specimens with different diamond thicknesses are depicted in Fig.8. It can be seen that the position of the maximum tensile stress changes with the substrate thickness. The maximum tensile stress position on PCD surface can remain unchanged when the thickness ratio of diamond table to substrate is less than 0.2, which indicates that one-time cut away of substrate procedure is very important to obtain accurately the maximum tensile stress of PCD table surface.

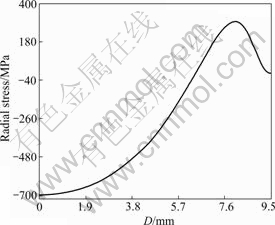
Fig.7 Radial residual stress on surface of diamond table

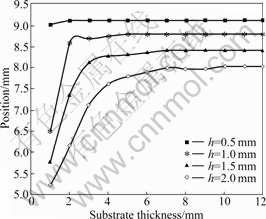
Fig.8 Variation of position of maximum tensile residual stress with respect to substrate thickness

3 Conclusions

1) Very high radial compressive residual stress near the compressive limit of PCD material can be induced in PDC cutter when being cooled from sintering temperature to room temperature. Radial tensile residual stress can also occur in diamond layer of PDC cutter. The maximum tensile stress occurs at the edge of diamond layer surface, which is harmful to PDC cutter, causing material fracture, cleavage and delamination failures.

2) The maximum compressive residual stress occurring at the center of interface is affected significantly by the thickness of diamond table. It can be a function of the thickness ratio of the diamond layer to carbide substrate layer. The lower the ratio, the less the radial compressive residual stress in the diamond table and the lower the radial tensile residual stress in the carbide substrate.

3) Location of the maximum tensile residual stress on diamond table surface varies with the thickness ratio of the diamond layer to carbide substrate layer. The obtained residual stress distribution feature in PDC cutter enables us to identify and mitigate harmful residual stresses in diamond layer.

References

[1] ZEREN M, KARAGOZ S. Sintering of polycrystalline diamond cutting tools [J]. Materials and Design, 2007, 28(3): 1055-1058.

[2] GITTEL H J. Cutting tool materials for high performance machining [J]. Industrial Diamond Review, 2001, 61(588): 17-21.

[3] TEASDAL P, RILEY N, MACKINNON P. New PDC technology delivers significant savings in Oman [J]. Journal of Petroleum Technology, 2005, 57(12): 66-67.

[4] XU Guo-ping, LIANG Hong-yuan, HE Li-min, LI Meng-hua. Development of high quality PDC for oil drilling [J]. Ming and Metallurgical Engineering, 2005, 25(4): 66-72. (in Chinese)

[5] LIU Sha, YI Dan-qing, YU Zhi-ming, LU Bin, WANG Jian-hua. Chemical pretreatments at surface of WC-6%Co for diamond coatings [J]. Transactions of Nonferrous Metals Society of China, 2002, 12(3): 396-399.

[6] ZHU Yong-wei, ZHANG Xin-ming, ZHOU Zhuo-ping, XIE Guang-zhuo. Study on interface between titanium-coated diamond and metal matrices [J]. Transactions of Nonferrous Metals Society of China, 2001, 11(5): 717-720.

[7] PAGGETT J W, DRAKE E F, KRAWITZ A D, WINHOLTZ R A, GRIEFIN N D. Residual stress and stress gradients in polycrystalline diamond [J]. Int J Refract Met Hard Mater, 2002, 20(3): 187-194.

[8] GONG Sheng-wu, ZHAO Fu-jun. Failure analysis of polycrystalline diamond compact cutters for breaking rock by bending waves theory [J]. J Cent South Univ Technol, 2008, 15(1): 112-116.

[9] JIAO Shu-jing, GAO Wan-fu. Interface conformations of polycrystalline diamond compact and their performances [J]. Diamond & Abrasives Engineering, 2004, 140(2): 61-66.

[10] BERTAQNOLLI K E, VALE R. Understanding and controlling residual stresses in thick polycrystalline diamond cutters for enhanced durability [C]// Proceedings of International Technical Conference on Diamond, Cubic Boron Nitride and their Applications. Vancouver, Canada, 2000.

[11] TIMOSHENKO S P, GOODIER J N. Theory of elasticity [M]. New York: McGraw-Hill Companies, 1970: 409-421.

[12] CAO Pin-lu, LIU Bao-chang, YIN Kun, ZHANG Zu-pei. Optimization design and residual thermal stress analysis of PDC functionally graded materials [J]. Journal of Zhejiang University: Science, 2006, 7(8): 1318-1323.

[13] LIN T P, HOOD M, COOPER G A, SMITH R H. Residual stresses in polycrystalline diamond compacts [J]. J Am Ceram Soc, 1994, 77(6): 1562-1568.

[14] ZHANG Gao-feng, ZHANG Bi, DENG Zhao-hui. Material removal mechanism of the grinding and polishing of PDC cutting tools [J]. Journal of Hunan University: Natural Sciences, 2008, 35(9): 33-38. (in Chinese)

[15] XU Gen, CHEN Feng, XU Guo-ping, MA Chun-de. Experimental research on the thermal residual stress distribution of polycrystalline diamond compacts [J]. Acta Mechanica Solida Sinia, 2009, 30(5): 459-467. (in Chinese)

(Edited by YANG Bing)