全螺旋灌注桩单桩极限承载力的预测
胡焕校1,刘 静2, 祝世平3
(1. 中南大学 地学与环境工程学院,湖南 长沙,410083;
2. 中南大学 土木建筑学院,湖南 长沙,410083;
3. 湖北中南勘察基础工程有限公司,湖北 武汉,430081)
摘 要:根据6根全螺旋灌注桩的实测桩顶载荷-桩顶沉降(Q-s)曲线,用双曲线法预测全螺旋灌注桩的极限承载力。研究结果表明:在极限加载范围内,用双曲线法能较好地预测全螺旋灌注桩的单桩极限承载力,拟合曲线与实测的曲线比较吻合且预测的结果偏于安全,预测结果的偏差与地层情况关系不大。
关键词:双曲线法;全螺旋灌注桩;单桩极限承载力
中图分类号:TU473.1 文献标识码:A 文章编号:1672-7207(2007)06-1239-06
Prediction of single ultimate bearing capacity of screwed casting pile
HU Huan-xiao1, LIU Jing2, ZHU Shi-ping3
(1. School of Geoscience and Environmental Engineering, Central South University, Changsha 410083, China;
2. School of Civil Architectural and Engineering, Central South University, Changsha 410083, China;
3. Hubei Central South Exploration and Foundation Engineering Co Ltd, Wuhan 430081, China)
Abstract: The ultimate bearing capacity of the single screwed pile was predicted based on the six piles with screws from four different sites by hyperbola method. The results show that the predicted curve is in good agreement with the field measurement curve below ultimate load, and tends to be safe. The deviation from prediction result to measured result is not closely connected with subterranean formation.
Key words: hyperbola method; the pile with screws; ultimate bearing capacity of single pile
单桩静载荷试验是确定单桩极限承载力的最直观、最可靠的方法之一,也是我国规范[1-2]规定的方法。在工程实践中,由于荷载装置、试桩费用、工程施工进度以及试验终止条件等限制,未能将试桩压至破坏,所得的Q-s曲线是不完整的,不能直接得到单桩极限承载力,因此,如何利用已获得的实测数据,合理地预测单桩极限承载力,国内外学者进行了大量研究,提出了多种数学模型预测方法[3-7],其中双曲线法是比较简单、适用、拟合精度较高的方法之一。但是,以前对桩承载力的预测只限于针对传统桩型,而很少对全螺旋灌注桩进行研究。
全螺旋灌注桩是一种全新桩型,它是在全螺旋预制桩基础上开发出来的,全螺旋预制桩虽然在日本应用已有20多年的历史,但其承载力主要是通过现场静荷载试验确定,在理论上没有进行承载力的研究[8];在国内,吴敏等[9-10]对全螺旋灌注桩的承载力进行了探讨。实际上,由于试验数据较少,理论研究成果少,全螺旋灌注桩单桩极限承载力只能通过现场静荷载试验确定。因此,通过预测的方法来估计全螺旋灌注桩的极限承载力具有现实意义。
1 双曲线法的基本原理
双曲线法是由克里斯顿(Christon)在1967年提出的[11-13]。该法假定试桩Q-s曲线符合双曲线方程,基本公式为:
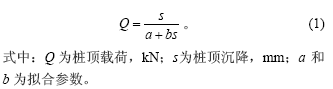

采用双曲线模型确定单桩极限承载力的方法常用的有2种。
方法一为沉降控制法,即根据有关规范要求取桩顶沉降为某一数值所对应的荷载为单桩极限承载力(如根据JGJ 94—94规范,对试桩Q-s曲线呈缓变形的,可取桩顶沉降40~60 mm所对应的荷载为单桩极限承载力),根据式(1)求得单桩极限承载力。
方法二为折减系数法(又称斜率倒数法或逆斜率法),即将计算所得的破坏荷载Qu取一定的折减系数得单桩极限承载力Quk [14]:
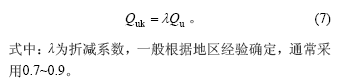
按式(1)~(6)计算时假定位移趋于无穷大时对应的荷载为极限荷载(确切地说为破坏荷载),故须再乘以经验性的修正系数λ才得到外推的极限承载力,本文取0.85。
Christon曾进行一系列对比平行试验研究,发现在s/Q与s之间存在着非常好的线性关系,并且在没有持续加荷至破坏的情况下,式(4)中的斜率倒数即1/b会反映出接近于观测值的破坏荷载。
根据Christon的推导,依据实际试桩资料,推算灌注桩极限承载力的步骤如下:
a. 根据试桩资料整理出Q-s曲线。
b. 因Q-s曲线最初为直线段,即弹性阶段,不属于双曲线范围,应将该段的Q和s已知坐标值舍去,不计入计算之列。
c. 选取Q-s曲线中双曲线部分的Q和s已知坐标值,并剔除明显的不合理点,按最小二乘法或用图解法计算公式(4)中的b。计算时,应至少已知4组可用的Q和s,以避免误差过大。
2 工程实例分析
本次工程实例共有6根桩,分别来自于不同的4个工地,全部设计为全螺旋灌注桩。其中:1号工地试桩1根(1号桩),设计桩径外径R为600 mm,内径r为350 mm,桩身无钢筋,桩长为13.5 m,设计要求单桩竖向极限承载力不低于2.4 MN;2号工地试桩1根(0号桩),桩长为4.8 m,外径R为500 mm,内径r为300 mm,桩身无钢筋,单桩竖向极限承载力为462 kN,极限承载力试验值对应的沉降为28.88 mm,该桩达到破坏时荷载为504 kN,破坏荷载对应的沉降量为41.73 mm;3号工地试桩2根(60号和7号桩),桩长为17 m,外径R为400 mm,内径r为270 mm,单桩极限承载力720 kN时沉降仅为5~12 mm;4号工地试桩2根(74号和219号桩),桩长为15 m,外径R为450 mm,内径r为270 mm,设计单桩竖向极限承载力不小于1.6 MN,单桩极限承载力1.6 MN时沉降不到15 mm。这6根桩中除2号工地试桩试验达到破坏荷载外,其他5根桩均因加载不够而未达到竖向极限承载力。由于这6根桩的Q-s曲线均表现为缓变型,其单桩竖向极限承载力未完全表征,为了统一,本次单桩竖向极限承载力的预测值均取沉降量s为40 mm时的承载力。工程实例所在4个不同场地的工程地质情况见表1。
根据现场测得的全螺旋灌注桩Q-s曲线,运用双曲线方法对6根桩的单桩极限承载力进行预估,预测结果见表2。
表1 各桩的工程地质情况
Table 1 Geotechnical information of all piles
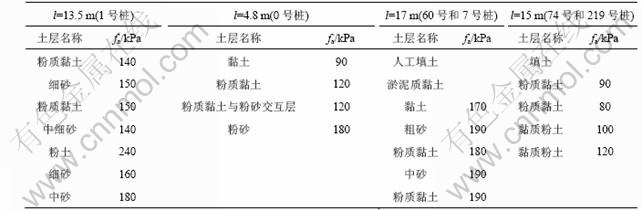
注:fa为地基承载力特征值;0号桩桩顶标高与7 m深的基坑底标高一致;l为桩长。
表 2 各桩的单桩竖向极限承载力预测结果
Table 2 Predicted values on ultimate bearing capacity of all piles
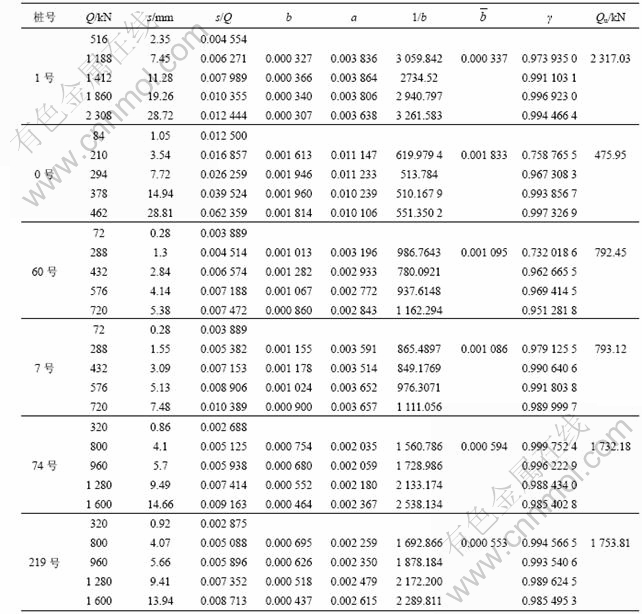
根据表2所示计算结果,利用式(1)绘出各桩的拟合Q-s曲线,并且与实测Q-s曲线进行比较,结果如图1~6所示。
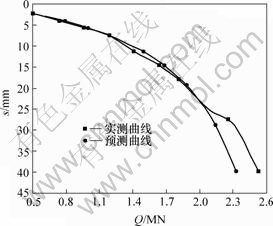
图 1 1号桩Q-s曲线
Fig.1 Q-s curves of pile No.1
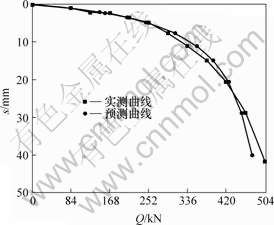
图 2 0号桩Q-s曲线
Fig.2 Q-s curves of pile No.0
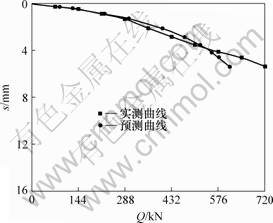
图 3 60号桩Q-s曲线
Fig.3 Q-s curves of pile No.60
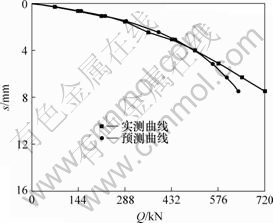
图 4 7号桩Q-s曲线
Fig.4 Q-s curves of pile No.7
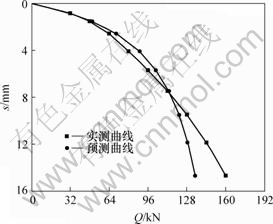
图 5 74号桩Q-s曲线
Fig.5 Q-s curves of pile No.74
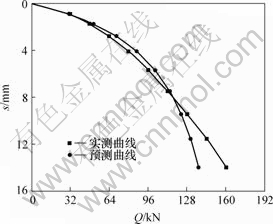
图 6 219号桩Q-s曲线
Fig.6 Q-s curves of pile No.219
3 预测结果分析
根据双曲线法的基本原理,虽然在拟合过程中剔除了加载初期处于弹性阶段的一级或者几级荷载作用下的Q和s坐标值,但是,由于全螺旋灌注桩是一种全新的桩型,对其承载机理还未真正了解,拟合的曲线出现一些偏离现象。
1号工地上1号桩的加载量较大,在前几级荷载作用下,桩基本上处于弹性状态和弹塑性状态。用这些Q和s坐标值拟合的曲线与实测曲线除在个别位置有一些小幅度的偏移外,整个拟合曲线与实测曲线比较吻合,但在最后2级荷载过程中,实测曲线突然表现为土的硬化过程,而拟合曲线预测单桩竖向极限承载力偏小,较实测值小8.5%。
2号工地上0号桩,其桩长仅为5.4 m,加载量比较大,基本上达到了极限承载力,用处于弹塑性阶段的Q和s坐标值拟合的曲线在极限加载范围内与实测曲线大致重合,只是在接近极限荷载时出现一定程度上的偏差。当实际加载为504 kN时,桩顶沉降量为41.73 mm,超过了规范要求[1]。用双曲线法拟合所得单桩竖向极限承载力为476 kN,该值与实测曲线反映的极限值偏差小于5.0%。
3号工地上60号和7号桩,4号工地上74号和219号桩,由于整个基桩在加荷过程中基本上处于弹性状态,用双曲线法拟合承载力较小,但用双曲线法拟合所得单桩竖向极限承载力很一致,其中60号和7号桩分别为792.45 kN和793.12 kN, 74号和219号桩分别为1 732.18 kN和1 753.81 kN,其相对误差分别为0.08%和1.25%,说明在同一场地,当各方面条件相同时, 全螺旋灌注桩单桩竖向极限承载力表现较稳定,反映出施工质量容易得到控制。
比较图1~6所示的预测曲线与实测曲线可以发现,总的来说,拟合曲线与实测曲线较吻合,是预测曲线在实测曲线的左侧,预测结果偏于安全。
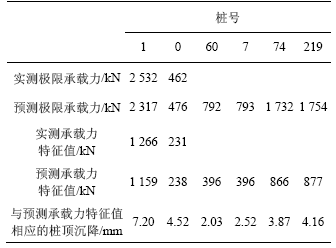
从所有桩的预测结果可以看出,用双曲线法预测的极限荷载较小,在各桩预测承载力特征值作用下桩顶的沉降值如表3所示(表中取安全系数K=2)。
表3 各桩预测承载力特征值下的沉降值
Table 3 Settlement under characteristic value of bearing capacity of every pile
本次选择的6根工程实例桩尽管分别取自于不同的4个工地,但用双曲线法拟合的全螺旋灌注桩的荷载沉降曲线与实测的曲线较吻合,说明用双曲线法预测全螺旋灌注桩单桩极限承载力比较可靠,也表明全螺旋灌注桩这种技术提供单桩极限承载力比较稳定,不因场地地层的不同而导致承载力出现非地层原因引起承载力的差异。
4 结 论
a. 双曲线法是一种较简单的预测桩基极限承载力的方法。
b. 在桩顶加载量与实际极限承载力相差过大时,拟合曲线与实测曲线出现一定程度上的偏差;在接近或者达到极限承载力的点上,用双曲线方法预测的承载力较实测值小;在设计荷载范围内,用双曲线法可以很好地拟合全螺旋灌注桩的Q-s曲线。
c. 用双曲线法预测的全螺旋灌注桩的荷载沉降曲线,总的发展趋势是预测曲线在实测曲线的左边,所以预测的结果偏于安全。
d. 在同一场地,当各方面条件相同时, 全螺旋灌注桩单桩竖向极限承载力表现较稳定,反映出施工质量容易得到控制。
e. 本次选择的6根工程实例桩分别取自于不同的4个工地,但用双曲线法拟合的全螺旋灌注桩的荷载沉降曲线与实测的曲线都较吻合,说明这种方法具有普遍性,可以用于工程实践。
参考文献:
[1] JGJ94—94, 建筑桩基技术规范[S].
JGJ94—94, Technique code for building pile foundation[S].
[2] GB50007—2002, 建筑地基基础设计规范[S].
GB50007—2002, Code for design of building foundation[S].
[3] 邓志勇, 陆培毅. 几种单桩竖向极限承载力预测模型的对比分析[J]. 岩土力学, 2002, 23(4): 428-431.
DENG Zhi-yong, LU Pei-yi. Comparison and analysis of several predicating models of ultimate bearing capacity of single pile[J]. Rock and Soil Mechanics, 2002, 23(4): 428-431.
[4] 赵明华, 刘 煜, 曹文贵. 软土路基沉降发展规律及其预测[J]. 中南大学学报: 自然科学版, 2004, 35(1): 157-161.
ZHAO Ming-hua, LIU Yu, CAO Wen-gui. The developing regularity and forecasting of settlement in soft clay roadbed[J]. Journal of Central Souh Universiy: Natral Science, 2004, 35(1): 157-161.
[5] 赵明华, 杨明辉, 刘 煜, 等. 软土路基固结沉降机理及其预测方法研究[J]. 铁道科学与工程学报, 2005, 2(4): 16-20.
ZHAO Ming-hua, YANG Ming-hui, LIU Yu, et al. Study on the developing and forecasting of the settlement in soft clay roadbed[J]. Journal of Railway Science and Engineering, 2005, 2(4): 16-20.
[6] 涂 帆, 常方强, 李小鹏. 指数法和双曲线法组合预测单桩极限承载力[J]. 福建工程学院学报, 2006, 4(1): 21-23.
TU Fan, CHANG Fang-qiang, LI Xiao-peng. Predicting ultimate bearing capacity of single cement mixing pile by exponential and hyperbola methods[J]. Journal of Fujian University of Technology, 2006, 4(1): 21-23.
[7] 赵春风, 于明章, 吴水根, 等. 试桩未达破坏时单桩极限承载力的估算方法[J]. 同济大学学报, 1999, 27(4): 474-477.
ZHAO Chun-feng, YU Ming-zhang, WU Shui-gen, et al. Method defining the bearing of single testing pile not reaching degree of failure[J]. Journal of Tongji University, 1999, 27(4): 474-477.
[8] 刘金励. 桩基础设计与计算[M]. 北京: 中国建筑工业出版社, 1990.
LIU Jin-li. Design and calculation on pile foundation[M]. Beijing: China Architecture and Building Press, 1990.
[9] 吴 敏, 李波扬. 全螺旋灌注桩-螺纹桩竖向承载力初探[J]. 武汉大学学报: 工学版, 2002, 35(5): 109-112.
WU Min, LI Bo-yang. Primary discussion on vertical load bearing capacity of screwed filling piles[J]. Engineering Journal of Wuhan University, 2002, 35(5): 109-112.
[10] 李波扬, 吴 敏. 一种新型的全螺旋灌注桩-螺纹桩[J]. 建筑结构, 2004, 34(4): 55-57.
LI Bo-yang, WU Min. A new screwed filling pile-screwed pile[J]. Building Structure, 2004, 34(4): 55-57.
[11] 刘俊龙. 双曲线法预测单桩极限承载力的讨论[J]. 岩土工程技术, 2001(4): 204-207.
LIU Jun-long. Discuss on forecasting ultimate bearing capacity of single pile by hyperbola method[J]. Gotechnical Engineering Technique, 2001(4): 204-207.
[12] 修朝英, 李大展. 单桩垂直静载试验P-S曲线的数学描述和极限荷载的预测[J]. 岩土工程学报, 1988, 10(1): 64-73.
XIU Zhao-ying, LI Da-zhan. Mathematical characterization of P-S curve & forecasting of ultimate load on vertical bearing capacity of single pile with static loading test[J]. Chinese Journal of Geotechnical Engineering, 1988, 10(1): 64-73.
[13] 祝龙根, 刘利民, 耿乃兴. 地基基础测试新技术[M]. 北京: 机械工业出版社, 2002: 147-148.
ZHU Long-gen, LIU Li-ming, GEN Nai-xin. New testing technology for groundsill foundation[M]. Beijing: China Mechine Press, 2002: 147-148.
[14] CHIN F K. The inverse slope as a prediction of ultimate bearing capacity of piles[C]//Proceedings of the 3rd South-East Asian Conference for Foundations, CP2004. Manila, 1972: 375-383.
[15] 齐 欢. 数学模型方法[M]. 武汉: 华中理工大学出版社, 1996.
QI Huan. The model method of mathematics[M]. Wuhan: Huazhong University of Technology Press, 1996.
收稿日期:2007-03-05;修回日期:2007-04-26
基金项目:中国冶金地质总局计划资助项目(2002年)
作者简介:胡焕校(1968-),男,浙江慈溪人,副教授,从事地质工程的教学与研究
通信作者:胡焕校,男,副教授;电话:0731-8876386;E-mail: hhx@mail.csu.edu.cn