J. Cent. South Univ. Technol. (2007)01-0115-05
DOI: 10.1007/s11771-007-0023-2
Experimental study on prediction model for maximum rebound ratio
LEI Wei-dong(雷卫东)1, TENG Jun(滕 军)1, A.HEFNY2, ZHAO Jian(赵 坚)3, 4, GUAN Jiong(关 炯)5
(1. Department of Urban and Civil Engineering, Shenzhen Graduate School, Harbin Institute of Technology,Shenzhen 518055, China;
2. School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore;
3. Ecole Polytechnique Federale de Lausanne (EPFL), Rock Mechanics Laboratory, Lausanne CH-1015, Switzerland;
4. College of Architecture and Civil Engineering, China University of Mining and Technology,Xuzhou 221008, China;
5. Kvaerner E&C Singapore Private limited, Aker Kvaerner Asia Pacific, Singapore 118254, Singapore)
Abstract: The proposed prediction model for estimating the maximum rebound ratio was applied to a field explosion test, Mandai test in Singapore. The estimated possible maximum peak particle velocities(PPVs) were compared with the field records. Three of the four available field-recorded PPVs lie exactly below the estimated possible maximum values as expected, while the fourth available field-recorded PPV lies close to and a bit higher than the estimated maximum possible PPV. The comparison results show that the predicted PPVs from the proposed prediction model for the maximum rebound ratio match the field-recorded PPVs better than those from two empirical formulae. The very good agreement between the estimated and field-recorded values validates the proposed prediction model for estimating PPV in a rock mass with a set of joints due to application of a two dimensional compressional wave at the boundary of a tunnel or a borehole.
Key words: blasting wave; maximum rebound ratio; joint stiffness; field explosion test
1 Introduction
When a blasting wave originating from a borehole propagates in rock masses with multiple parallel joints (supposing there are not any more joints afterwards) along the radian direction normal to the joints, the wave at the points behind the last joint in the set is only the transmitted wave. Therefore, the value of peak particle velocity(PPV) at any point behind the last joint can be estimated by the proposed prediction model for the transmission ratio (Tn)[1]. However, very often, joints exist in a rock mass in a whole set or several sets, rather than multiple joints. In the process of blasting wave propagation through a whole joint set, superposition of the multiple reflected and transmitted waves occurs between two adjacent joints in the joint set. The PPV at any point between two adjacent joints in the joint set is controlled by the superposition of the multiple reflected and the transmitted waves, which can be measured by the rebound ratio. The maximum rebound ratio (Rn, max, where n stands for the joint number among all the grid-points between two adjacent joints in a joint set can be estimated by the prediction model for the maximum rebound ratio, as the upper limit of the ratio of the wave amplitude from the model with joints to the wave amplitude from the model of intact rock. This model was developed in Ref.[2].
In a real joint set, very often, it is practically impossible to fully know the relative position between the monitoring point and the two adjacent joints. Therefore, if the proposed prediction model for estimating the maximum rebound ratio is reliable, the field-recorded PPV at a monitoring point should be equivalent to or lower than the estimated PPV from the prediction model for estimating the maximum rebound ratio.
In this study, a reported explosion test in a jointed rock mass was introduced which was conducted in a quarry site in Mandai, Singapore[3-4]. The Mandai explosion test was a part of a research program to study the wave propagation in fractured rock masses and the effects on the existing underground structures. There were 5 monitoring boreholes (BHs 1, 2, 3, 4 and 5) located along a line in the rock mass. For all the five monitoring boreholes, PPVs at the monitoring points were recorded. The PPVs at the locations of the monitoring points in the field were estimated by the methods proposed in Ref.[2]. The estimated PPVs were compared with the field records and the solutions from two available empirical formulae. The comparison serves as the verification of the proposed prediction models for estimating the maximum rebound ratio.
2 Briefing of explosion test
2.1 Configuration of test and field records
The site of Mandai test was in the rock mass containing Bukit Timah granite. A vertical charge hole of about 11 m in depth was drilled. The charge chamber was 4.2 m in height and 0.8 m in diameter, lined with concrete blocks. The explosive charge was placed at the center of the charge chamber. Before the explosion, the charge chamber was covered by a steel plate and concrete blocks. The explosive charge was 41.5 kg TNT in charge mass equivalent to 20 kg/m3 in loading density (the mass is divided by the chamber volume). Five vertical instrumentation boreholes of 0.2 m in diameter were drilled along the bearing of 230? from the north. Three of the five boreholes were 14 m in depth and the other two were 8.5 m in depth. The locations of the boreholes (BHs 1, 2, 3, 4 and 5) were 2.5, 5.0, 10.0, 25.0 and 50.0 m from the center of the charge hole, respectively. Table 1 lists the field-recorded PPVs at the five monitoring points.
Table 1 Field-recorded PPVs at five monitoring points

2.2 Parameters involved in estimating maximum PPV at monitoring points
The parameters involved in estimating the maximum rebound ratio, Rn,max at the monitoring points are systematically specified as follows.
1) The properties of the intact rock: The properties of the intact rock, Bukit Timah granite, are determined from extensive laboratory testing program and shown in Table 2[5].
2) Characteristics of the blasting wave modeled in Autodyn: Autodyn is a continuum-based program that requires the jointed rock mass to be converted into its equivalent continuous rock (i.e. elastic modulus and shear modulus of the in-situ equivalent rock mass, Ee and Ge, are required as the input, rather than elastic modulus and shear modulus of the intact rock, Er and Gr). Therefore, firstly, according to the quality of the intact rock and the joint conditions from site investigation, the rock mass rating(RMR) of the in-situ rock mass is calculated based on RMR system[6]. And then, elastic modulus Ee of the in-situ equivalent continuous rock is estimated by the relationship between Ee and RMR[7]. Finally, the shear modulus Ge of the in-situ equivalent continuous rock is calculated accordingly.
Table 2 Mechanical properties of Bukit Timah granite

With the properties of the in-situ equivalent continuous rock mass and the properties of the explosive used in Mandai test, modeled in Autodyn, the properties of the input velocity pulse are obtained as: frequency is 700 Hz, amplitude of the compressional wave is 3.07 m/s.
3) The normalized normal stiffness of the joint: Besides the characteristics of the blasting wave need to be determined, in order to apply the proposed model for estimating Rn,max, the normalized normal stiffness of the joint in the site must be determined as well.
Based on the obtained properties of the in-situ equivalent continuous rock mass, Ee and Ge, as well as the joint spacing which can be obtained in-situ investigation, the normal stiffness of the joint can be obtained by using the formula proposed by HART[8] as: kn=42.7 GPa/m, therefore, the corresponding normalized normal stiffness kn/(ωz) is determined as 0.695 for the Mandai test. The terms of kn/(ωz) is the normalized normal stiffness of the joints, ω is the angular frequency of the wave, z equivalent to ρcP is wave impedance, ρ for density of the rock and cP for P-wave speed.
4) According to the in-situ investigation, the spacing of the joints is 2.5 m, hence the ratio of joint spacing to wavelength is calculated as 0.33 for the Mandai test.
2.3 Relative position between monitoring points and joint set
The joints in the granite are mapped in the quarry and inferred from boreholes using impression packer data. Generally, there are two predominantly sub-vertical joint sets, with strike directions of 140? and 230? respectively, perpendicularly intersecting each other. Among the existing joint sets in the field, the strike of the most dominant joint set is 140?[9-10], perpendicular to the line along which the monitoring boreholes are located.
In Mandai test, when the 2-D compressional wave from the charge hole travels in the in-situ rock mass, it is reasonable to assume that the peak particle velocities corresponding to the points along the monitoring line with the bearing of 230? are dominated by the joint set with strike of 140? which is perpendicular to the monitoring line. The joint set (with strike of 230?) parallel to the monitoring line is assumed to have negligible effects on the PPVs at the monitoring points. It should be noted that an independent study using universal distinct element code(UDEC) has confirmed this assumption.
Therefore, the relative position between the monitoring points and the most dominant joint set with strike of 140? is shown in Fig.1.
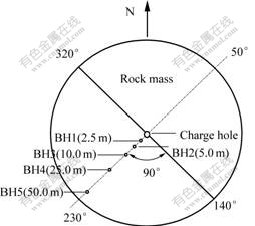
Fig.1 Relative position between monitoring points and most dominant joint set
For estimation purpose, a schematic diagram of the Mandai test showing the relative position between the field monitoring points and the joints in the rock mass is shown in Fig.2. The explosion load is applied to the boundary of the borehole. The monitoring points are supposed to be along the radial line normal to the joints. Table 3 lists the numbers of joints that the compressional wave crosses before reaching the monitoring points.
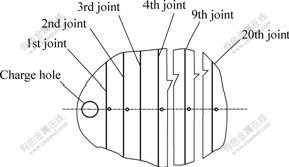
Fig.2 Schematic diagram of Mandai test for estimating Rn,max
Table 3 Number of joints compressional wave crosses before reaching monitoring points

3 Verification of proposed model for estimating Rn,max
3.1 2-D compressional wave propagation in intact rock
As an important potential application of the proposed model for estimating the maximum rebound ratio Rn,.max, the proposed model can be used to estimate the upper limit of the PPVs, not only the wave amplitude ratio (such as the transmission ratio Tn or the maximum rebound ratio Rn,max) at the monitoring points in a blasting wave propagation problem. However this important application is based on the analysis results in 2-D compressional wave propagation in an intact rock. Therefore, in this sub-section, the result in 2-D compressional wave propagation in intact rock for the case of wave frequency of 700 Hz is introduced before the verification example is presented.
An independent study on 2-D compressional velocity wave (from the boundary of a circular cavity) propagation in an intact rock has been performed[11]. In the study, a very important concept, scaled distance ((R-R0)/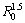 ) is proposed, where R is the radial distance from the cavity center, and R0 is the radius of the cavity from which the compressional velocity originates. It is found that the amplitude of the velocity wave at any point with the same value of (R-R0)/
) is proposed, where R is the radial distance from the cavity center, and R0 is the radius of the cavity from which the compressional velocity originates. It is found that the amplitude of the velocity wave at any point with the same value of (R-R0)/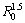 is independent of the radius of the cavity, from which the compressional velocity wave originates. Several charts have been prepared for checking the amplitude corresponding to any point in the surrounding intact rock. In the prepared charts, the wave amplitude at any point in the surrounding intact rock can be determined, for an input compressional velocity wave with unity amplitude for any frequency. Fig.3 shows the amplitude of the velocity wave at any point in the surrounding intact rock vs the scaled distance (R-R0)/
is independent of the radius of the cavity, from which the compressional velocity wave originates. Several charts have been prepared for checking the amplitude corresponding to any point in the surrounding intact rock. In the prepared charts, the wave amplitude at any point in the surrounding intact rock can be determined, for an input compressional velocity wave with unity amplitude for any frequency. Fig.3 shows the amplitude of the velocity wave at any point in the surrounding intact rock vs the scaled distance (R-R0)/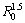 at the frequency of 700 Hz.
at the frequency of 700 Hz.
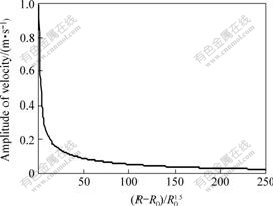
Fig.3 Amplitude of velocity wave vs scaled distance ((R-R0)/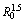 ) at wave frequency of 700 Hz
) at wave frequency of 700 Hz
3.2 Comparison between field records and estimated PPVs
From Fig.2, it can be seen that the 1st, 2nd, 3rd, 4th and 5th monitoring point in Mandai test is located before the 2nd, 3rd, 5th, 10th and 21st joint, respectively, from the boundary of the borehole. In this part, several maximum rebound ratios, R2,max, R3,max,R5,max, R10,max and R21,max are estimated based on the curves as shown in Figs.3(a)-(e) in Ref.[2]. Among these maximum rebound ratios, the procedure of estimating R10,max is introduced in detail.
First, according to the target value of kn/(ωz) of 0.695, Figs.3(d) and (e) in Ref.[2] are chosen for linear interpolation, because Figs.3(d) and (e) in Ref.[2] correspond to kn/(ωz) of 0.448 and 0.897, defining a range covering the target value of kn/(ωz) of 0.695.
Table 4 lists the data drawn from Figs.3(d) and (e) in Ref.[2], involved in estimating the maximum rebound ratio before the 10th joint in the joint set spaced at 0.33 wavelength, with kn/(ωz) of 0.695, in the radian direction normal to the joints.
Table 4 R10,max for ratios of spacing to wavelength of 0.3 and 0.4, kn/(ωz) of 0.897 and 0.448
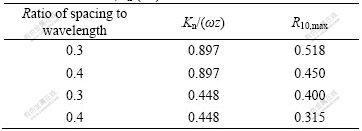
In Table 4, fixing the number of joints and the normalized normal stiffness kn/(ωz), taking the ratio of spacing to wavelength as a variable, for the target ratio of spacing to wavelength of 0.33, by linear interpolation, R10,max can be calculated for kn/(ωz) of 0.897 and 0.448 respectively as 0.498 and 0.375.
Hence R10,max for the ratio of spacing to wavelength of 0.33 and kn/(ωz) of 0.695 can be calculated by linear interpolation as 0.443.
Repeating the same procedure for estimating R10,max, other maximum rebound ratios, R2,max, R3,max,. R5,max and R21,max can be obtained. Table 5 lists R2,max, R3,max, R5,max, R10,max and R21,max of the 2nd, 3rd, 5th, 10th and 21st joints in a joint set spaced at 0.33 wavelength, with kn/(ωz) of 0.695, in the radian direction normal to the joints.
The maximum possible PPV corresponding to a monitoring point is the product of the estimated maximum rebound ratio Rn,max by the amplitude of the compressional pulse wave corresponding to the same monitoring point from the model of intact rock. The amplitude of the wave at any point for the case of intact rock can be determined using Fig.3(It is noted that the amplitude from Fig.3 is for the input wave with unity amplitude. Therefore, the amplitude value from Fig.3 is multiplied by 3.07, i.e. the amplitude of the input wave in Mandai test). Table 6 lists the estimated maximum possible PPVs and the field records.
Table 5 Several maximum rebound ratios

The estimated maximum possible PPVs from the prediction model and the field-recorded PPVs are compared in Fig.4. The horizontal axis in Fig.4 represents the scaled range (rm-1/3), where r is the radial distance, from the explosion source, m; m is the charge mass, kg. The solutions from two available empirical formulae (WU formula and AMBRASEYS and HENDRON formula) are also included in Fig.4. AMBRASEYS and HENDRON[12] suggested an empirical formula as: PPV=11.45(rm-1/3)-2.8, for (rm-1/3)<4.14 and PPV= 2.08(rm-1/3)-1.6, if (rm-1/3)≥4.14; while WU[13] suggested PPV=1.8(rm-1/3)- 2.5.
In the field, every monitoring point is between two adjacent joints, the field records are PPVs of the superposition of the multiple reflected and transmitted waves, not only of the transmitted wave. Because of the uncertainty of the relative position of the monitoring point and the two adjacent joints in the joint set, the field-recorded PPV corresponding to a monitoring point should be below or equal to the estimated PPV from the proposed prediction model for estimating the maximum rebound ratio.
Table 6 Estimated maximum possible PPVs and field records

From Fig.4, it can be seen that the estimated maximum possible PPVs agree well with the field-recorded PPVs. Three of the four available field-recorded PPVs lie exactly below the estimated PPVs as expected, while the fourth available field-recorded PPV lies close to and a bit higher than the maximum estimated PPV. The very good agreement between the estimated and field-recorded values validates the proposed prediction model for estimating peak particle velocity in a rock mass with multiple parallel joints due to application of a compressional wave at the boundary of a tunnel or a borehole.
It can also be seen from Fig.4, that the results from both of the two available empirical formulae match with the field data poorer than the results from the prediction models for the maximum rebound ratio proposed in this research. This is because all the factors (i.e. the normalized normal stiffness of the joint, the joint spacing and the characteristics of the input wave) influencing the maximum rebound ratio in the process of 2-D compressional wave propagation in a jointed rock mass are taken into account in this research. By contrast, only the distance of the monitoring points and explosion charge were considered in the available empirical formulae, while the properties of the joint were not taken into account.
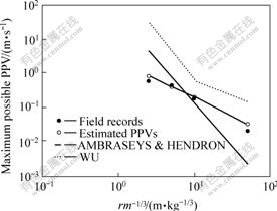
Fig. 4 Comparison among estimated maximum possible PPVs from prediction model, field records and PPVs from two empirical formulae
4 Conclusions
1) The estimated maximum possible PPVs at the monitoring points from the proposed prediction model agree well with the field-recorded PPVs, indicating that the proposed prediction model for estimating the maximum rebound ratio along the radian direction normal to the joints is reliable.
2) Taking all the factors influencing the maximum rebound ratio in the process of 2-D compressional wave propagation in a jointed rock mass into account, the solutions from the prediction model proposed in this research agree with the field test records better than those from the available empirical formulae.
References
[1] LEI W D, TENG J, ZHAO J, et al. A study on transmission ratio (Tn) in the radian direction normal to joints in 2-D compressional wave propagation in rock masses[J]. Journal of University of Science and Technology Beijing, 2006, 13(3):199-206.
[2] LEI W D, TENG J, ZHAO J, et al. Numerical study on maximum rebound ratio in blasting wave propagation along radian direction normal to joints [J]. Journal of Central South University of Technology, 2006, 13(6): 743-748.
[3] CHEN S G, CAI J G, ZHAO J, et al. Discrete element modeling of an underground explosion in jointed rock mass[J]. Geotechnical and Geological Engineering, 2000, 18(2): 59-78.
[4] CHEN S G, ZHAO J, ZHOU Y X. UDEC modelling of a field explosion test[J]. Fragblast – International Journal of Blasting and Fragmentation, 2000, 4(2): 149-163.
[5] LEE C B. Fracturing characteristics of Bukit Timah granite [D]. Singapore: Nanyang Technological University, 2002.
[6] BIENIAWSKI Z T. Engineering classification of joint rock masses [J]. The Civil Engineer in South Africa, 1973,15(12): 335-343.
[7] SERAFIM J L, PEREIRA J P. Consideration of the geomechanical classification of Bieniawski[C]// Proceedings of International Symposium on Engineering Geology and Underground Construction, Lisbon: Portugal, 1983: 33-44.
[8] HART R D. An Introduction to distinct element modeling for rock engineering[C]// HUDSON J A. Comprehensive Rock Engineering. Oxford: Pergamon Press, 1993: 245-261.
[9] ZHAO J, HEFNY M A, ZHOU Y X. Hydrofracturing in-situ stress measurement in Singapore granite [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 577-583.
[10] ZHAO J. Construction and utilization of rock caverns in Singapore, part A: bedrock resource of the Bukit Timah granite[J]. Tunnelling and Underground Space Technology, 1996, 11(1): 65-72.
[11] LEI Wei-dong. Numerical Studies on 2-D Compressional Wave Propagation in Jointed Rock Masses[D]. Singapore: Nanyang Technological University, 2005.
[12] AMBRASEYS N R, HENDRON A J. Dynamic behavior of rock masses[C]// Proceedings of Rock Mechanics in Engineering Practice. London: John Wiley and Sons, 1968: 203-227.
[13] WU T H. Soil Dynamics[M]. Boston: Allyn and Bacon, 1975.
(Edited by CHEN Wei-ping)
Foundation item: Project(50278057) supported by the National Natural Science Foundation of China; project(2002CB412703) supported by the Major State Basic Research Development Program of China
Received date: 2006-05-26; Accepted date: 2006-07-18
Corresponding author: LEI Wei-dong, PhD; Tel: +86-755-26033506; E-mail: wdlei@hitsz.edu.cn