Mathematical module for countercurrently fractional

chiral extraction and its VB simulation

TANG Ke-wen(唐课文)^{1, 2}, HUANG Ke-long(黄可龙)¹, YI Jian-min(易健民)^{1, 2}, ZHANG Guo-li(张国丽)¹

1. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China;

2. Department of Chemistry and Chemical Engineering, Hunan Institute of Science and Technology,

Yueyang 414000, China

Received 6 January 2006; accepted 27 March 2006

Abstract: Based on chemical thermodynamics and mass balance, countercurrently fractional chiral extraction by hollow fiber membrane was investigated. The mathematical modules for the relation of chiral extraction yield and product optical purity with number of transfer units by chiral extraction with hollow fiber membrane were established, and the modules were simulated by visual basic(VB) proceduce. The results show that, the difference in free energy between two diastereomeric complexes formed by R- and S-enantiomer with chiral selector, -?(?G), is the force of separation of enantiomers. It is necessary to separate enantiomers, where one of the extraction factors is above 1, and the other is below 1. Under certain phase ratio, chiral separation depends on separation factor and number of transfer units. The experimental result is in agreement with the theoretical value.

Key words: fractional chiral extraction; mathematical modules; VB simulation

1 Introduction

At molecular level, chirality represents substantial properties of life. For example, such life substances as protein, amylose, and nucleic acid are almost chiral. Most of drugs are chiral, the pharmacological functions of which are realized by molecular recognition. It is indicated by modern medicine that the different enantiomers of a drug can have vastly different pharmacological activities, pharmacokinetic processes, and toxicities[1,2]. Usually, a single-enantiomer drug has remarkable pharmacological activity, but the other has none or opposite pharmacological activity, even cause toxicity. This maybe exists in pesticides and protection of crops. Because of inactive or lower-active enantiomers, the degree of pollution will be enlarged if the appropriate single-enantiomer isn’t obtained. So how to obtain stereochemically pure drugs becomes one of the hot-topics in the world.

It is one of the important means to obtain a single- enantiomer drug by separation of racemic enantiomers. So such separation techniques as crystallization, enzymatic conversion and chromatography have been developed, but there are still some deficiencies about them. Today, preparative separations of enantiomers in a large scale are very limited. It is quite potential to separate enantiomers by chiral extraction which is highly regarded by the majority of investigators recently[3-7].

Membrane extraction is a new separation technique which combines liquid-liquid extraction with the membrane. Especially, hollow fiber membrane fractional extraction is a popular subject. Great progress has been made in such applications as metal ion extraction, organic extraction, pharmaceutical extraction and enzymatic transformation[8-11]. However, preparative separations of racemic compounds in a large scale by liquid-liquid extraction combining with hollow fiber membrane, are rarely reported.

In this study, based on thermodynamics and mass balance, the theory of distribution balance for chiral liquid-liquid extraction is studied. And mathematical modules of counter currently fractional chiral extraction with hollow fiber membrane are established and simulated by VB. It provides theory for separation of racemic mixtures by chiral extraction.

2 Theory of two phase distribution equi- librium

During the process of the liquid-liquid extraction, the aqueous phase and organic phase can be taken as a whole, and every material follows the equation of mass balance in the system:

X_i+βY_i=X_i0+βY_i0                              (1)

where  X_i and Y_i represent the total density of a material in aqueous and organic phase in equilibrium, respectively; X_i0 and Y_i0 represent the total density of a material in aqueous and organic phase before extraction, respectively; β is the phase ratio, β=V_org/V_aq.

For chiral extraction, the following equations can be obtained:

X_R+βY_R=X_R0+βY_R0                            (2)

X_S+βY_S=X_S0+βY_S0                             (3)

and two distribution coefficients K_R and K_S are

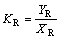                                  (4)

                                   (5)

Enantiomeric excess(E_e) reflects the purity of the extraction products:

                             (6)

E_{e, aq} and E_{e, org} in aqueous and organic phase can be written as

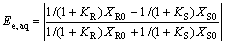         (7)

and

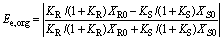          (8)

Usually, following equations are used to show the optical purity of the products:

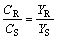                                  (9)

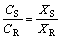                                 (10)

During chiral extraction, selector forms diastereomers with enantiomers depending on many kinds of molecule forces such as polarization, induction, electrostatics and hydrogenolysis:

R + LR-L                            (11)

S + LS-L                            (12)

or

R + DR-D                           (13)

S + DS-D                            (14)

These are differences in stability between the two diastereomers of R-L and S-L or R-D and S-D in hydrophobic organic solvent. -?(?G) can represent the difference of their free energy, and can be calculated:

-?(?G)= -?G_R-(-?G_S)=RTlnK_R-RTlnK_S

=RTlnK_R/K_S=RTlnα                    (15)

Separation of enantiomers is not merely influenced by K_R and K_S, but mainly depends on -Δ(ΔG). α is the separation factor which is a very important parameter of chiral extraction. -?(?G) reflects the ability of separation of enantoimers. In theory, so long as -Δ(ΔG) is not equal to 0, that is to say α is bigger than 1, separation of enantiomers can be realized under certain number of transfer units.

3 Establishment of mathematical modules of fractional chiral extraction

Fractional liquid-liquid extraction with hollow fiber membrane is described as traditional liquid-liquid equation. The design equation can be written as

L=H_t×N_t                                  (16)

where  L is the length of hollow fiber membrane, H_t is the height of a transfer unit, and N_t is the number of transfer units.

Under condition that the experiment is close to the balance, N_t is calculated from

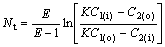                 (17)

where  E is the extraction factor (E=KB/A, A and B are the flow rates of water and organic solvent, respectively);  C_1(i) and C_1(o) are solute densities in water at entrance and export, respectively; C_2(i) and C_2(o) are solute densities in the organic phase at the entrance and export, respectively.

Then the mathematical modules of counter currently fractional chiral extraction with hollow fiber supported-liquid membrane are studied, as shown in Fig.1. First, the organic phase containing chiral selector is pumped into the side of tube. After it is full of organic phase, stop pumping it. Then the water phase is pumped into hollow fibre membrane. When it is full of aqueous solution, the organic phase begins to be pumped into the side of tube again. When the velocities of flow of the organic phase and the water phase are steady, raw material liquid including racemic mixtures is introduced to water phase through three valves.

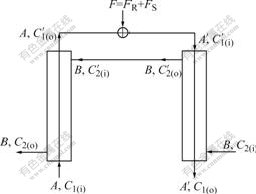
Fig.1 Schematic diagram of hollow fiber membrane extraction

Before studying chiral extraction, the inchiral extraction is discussed firstly.

The whole extraction system takes the following equation of mass balance:

F=AC_1(o)+BC_2(o)                            (18)

Because the flow rates of F is far smaller than A , A′ can be thought to be equal to A.

The whole extraction system can be divided into two models of extraction (extraction post I and counter extraction postⅡ), and these two models still accord with the theory of extraction. If the number of transfer units of the whole system is N_t, the number of transfer units of post I and postⅡare all N_t/2.

For model I, Eqn.(18) becomes

AC′_1(i)+BC_2(i)=AC_1(o)+BC′_2(o)                   (19)

Deduction from Eqn.(17 ) with E=KB/A and C_2(i)=0 results in

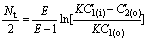                    (20)

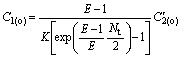               (21)

For model Ⅱ, there also exists

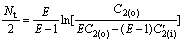               (22)

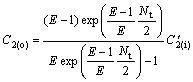             (23)

Because of C′_2(i)=C′_2(o), C_2(o)/C_1(o) can be calculated by

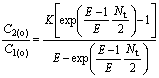                  (24)

So the extraction yield of the solute in the organic phase (Y_B) and water phase(Y_A) are written as

              (25)

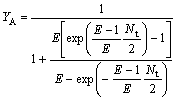               (26)

For chiral extraction, Eqn.(24 ) can be written as

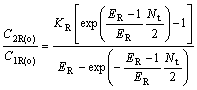             (27)

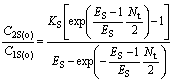                (28)

Deduction from Eqn.(27 ) gives

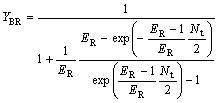         (29)

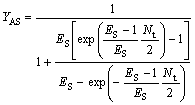             (30)

where Y_BR and Y_AS are the extraction yields of R-enantiomer in the organic phase and S-enantiomer in water phase, respectively.

For racemete(F_R=F_S), Eqn.(18) becomes two equations

AC_1R(o)+BC_2R(o)=F_R                         (31)

AC_1S(o)+BC_2S(o)=F_S                           (32)

Deduction from Eqns.(24), (31) and (32) yields

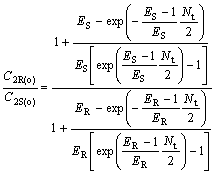          (33)

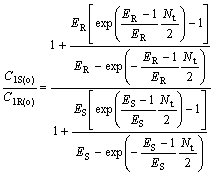          (34)

where  C_2R(o)/C_2S(o) and C_1S(o)/C_1R(o) are the optical purity of the enantiomers in organic and water phase, respectively.

From Eqns.(33) and (34), it can be deduced that chiral separation can’t be realized under condition that E_R is equal to E_S(K_R =K_S), and E_R and E_S are all bigger than 1, or E_R and E_S are all smaller than 1, respectively. E is a very important parameter for chiral extraction. Only when K_R is not equal to K_S, that’s to say, -?(?G) is not equal to 0, racemetes can be separated.

4 Simulation of mathematical modules by      VB

4.1 Determination of B/A

VB(visual basic) procedure is designed to simulate the relation among B/A, the optical purity of product(P) and the yield(Y). When K_R=1.2, K_S=1.02, N_t=20, 40 and 60, the relations of optical purity of products with B/A are simulated in Fig.2. It can be found from Fig.2 that under different N_t, C_2R(o)/C_2S(o) all decrease with the increase of B/A, but C_1S(o)/C_1R(o) all rise with the increase of B/A. In practical operation, we can take the value at the point of intersection of the two curves as B/A, which helps separate enantiomers by extraction.

4.2 Simulation of P and Y with N_t

Fig.3 reflects the relation between P and N_t under α=1.08, 1.18, 1.30, and 1.50, respectively. It can be found from Fig.3 that P rises with increase of N_t, and there is strong influence of α on chiral separation, that is to say, the extraction system with a bigger α needs less N_t than that with a smaller one.

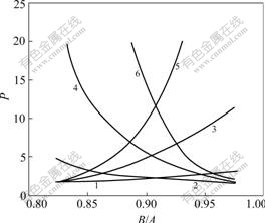
Fig.2 Relation between P and B/A (K_R=1.2, K_S=1.02): 1 C_S/C_R, N_t=20; 2 C_R/C_S, N_t=20; 3 C_S/C_R, N_t=40; 4 C_R/C_S, N_t=40; 5 C_S/C_R, N_t=60; 6 C_R/C_S, N_t=60

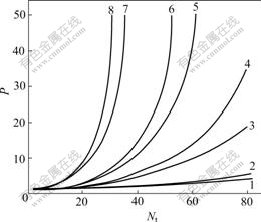
Fig.3 Relation between optics purity and N_t: 1 C_R/C_S, α=1.08; 2 C_S/C_R, α=1.08; 3 C_R/C_S, α=1.18; 4 C_S/C_R, α=1.18; 5 C_R/C_S, α=1.30; 6 C_S/C_R, α=1.30; 7 C_R/C_S; 8 C_S/C_R, α=1.50

Fig.4 reflects the relation between Y and N_t under α=1.08, 1.18, 1.30, and 1.50, respectively. It is found from Fig.4 that Y values of R-enantiomer in organic phase all rise with increase of N_t; Y values of S-enantiomer in water phase reduce with increase of N_t first, then rise; finally, all Y values tend towards 1; and much less N_t is needed for Y of the extraction system with a bigger α to be close to 1 than that with a smallr α.

4.3 Application

To examine the module, ofloxacin enantiomers were separated by 2×5 hollow fiber membrane extraction. Fig.5 reflects the relations of R/S in water at entrance with time. It is found from Fig.5 that the R/S reaches balance after 20 h and is 3.4. From 2×1 hollow fiber membrane extraction experimental results, it is concluded that N_t of 2×1 hollow fiber membrane is 8, and N_t of 2×5 hollow fiber membrane is 40. In theory, R/S in water at entrance by 2×5 hollow fiber membrane extraction should be 3.54, so the experimental result is almost in agreement with theoretical value.

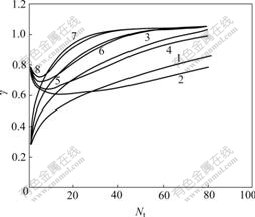
Fig.4 Relation between Y and N_t: 1 Y_AS, α=1.08; 2Y_BR, α=1.08; 3 Y_AS, α=1.18; 4 Y_BR, α=1.18; 5 Y_AS, α=1.30; 6 Y_BR, α=1.30; 7 Y_AS, α=1.50; 8 Y_BR, α=1.50

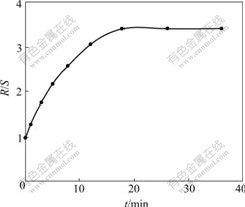
Fig.5 Optical purity of outflows as function of time by fractional extraction with gel-coated hollow fibers: A=0.5 mL/min, B=0.14 mL/min

5 Conclusions

1) The difference in free energy between two diastereomeric complexes formed by R- and S-enantiomer with chiral selector, -?(?G), is the force of separation of enantiomers.

2) It is necessary to separate enantiomers, in which one of the extraction factors is above 1, and the other is below 1. In practical operation, the value at the point of intersection of the two curves for relation between P and B/A is taken as B/A, which helps separate enantimers by extraction.

3) Under certain B/A, chiral separation depends on α and N_t.

4) The experimental result is in agreement with the theoretical value.

References

[1] ROSA H H, PILAR C F. Chromatographic separation of chlothalidone enantiomers using β-cyclodextrins as chiral additives [J]. J Chromatogr B, 2000, 740: 169-177.

[2] ABOLFAZL S M, ROBERT T F. Pharmacokinetics of metoprolol enantiomers following single and mutiple administration of racemate in rat [J]. Internal J Pharm, 2000, 22: 97-102.

[3] CEN Zhong-zhe, CAI Shui-hong. Solvent extraction of ephedrine epimerides with chiralagents [J]. J Chemical Industry and Engineering, 2000, 51(3): 418-420.

[4] VLADIMIR P, MI?E K, MARTIN E. Lipophilic tartaric acid esters as enantioselective ionophores [J]. Angew Chem, 1989, 28: 11475.

[5] J?R?ME L, CATHERINE G G, SONYA T H, JONATHAN J J. Efficient enantioselective extraction tris (diimine) ruthenium(Ⅱ) complexs by chiral, lipophilic trisphat anions [J]. Angew Chem, 2000, 39(20): 3695-3697.

[6] TANG Ke-wen, ZHOU Chun-shan, JIANG Xin-yu. Separation of ofloxacin enatiomers by extraction with solvent containing chiral selector [J]. Acta Pharmaceutical Sinica, 2002, 37(12): 967-970.

[7] TANG Ke-wen, ZHOU Chun-shan, JIANG Xin-yu. Racemic ofloxacin separationby supported-liquid membrane extraction with two organic phases [J]. Science in China, 2002, 36(6): 491-496.

[8] VALENZUELA F, BASUALTO C, TAPIA C. Application of hollow-fiber supported liquid membranes technique to the selective recovery of a low content of copper from a Chilean mine water [J]. J Membr Sci, 1999, 155: 163-168.

[9] JUANG R S, HUANG R H, WU R T. Separation of citric and lactic acids in aqueous solutions by solvent extraction liquid membrane processes [J]. J Membr Sci, 1997, 136: 89-99.

[10] WANG Yu-ju, LUO Guang-shen, DAI You-yuan. Research on removal of sulfanilic acid from water with membrane extraction [J]. Modern Chemical Industry, 2000, 10: 31-33.

[11] WANG Yu-jie, ZHANG Shu-min, LI De. Separation of Th⁴⁺ and Re³⁺ with hollow fiber membrane extraction [J]. J Chinese Rare Earth Society, 1998, 9: 193-198.

(Edited by YANG Bing)

Foundation item: Project(20576029) supported by the National Natural Science Foundation of China; Project(2004035650) supported by the China Postdoctoral Science Foundation

Corresponding author: HUANG Ke-long; Tel: +86-731-8879850; E-mail: klhuang@mail.csu.edu.cn