DOI: 10.11817/j.issn.1672-7207.2017.01.014
蜗杆砂轮曲面与面齿轮齿面的对应关系
唐进元，周恒
(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)
摘要：研究蜗杆砂轮磨削面齿轮的原理与方法。利用产形插齿刀作为中间曲面，通过计算面齿轮和插齿刀、插齿刀与蜗杆砂轮的接触线，得到蜗杆砂轮和面齿轮处于不同加工位置的接触点计算方法，给出蜗杆砂轮磨削面与面齿轮齿面对应关系模型，在VERICUT仿真软件中对蜗杆砂轮磨削面齿轮的方法进行仿真验证。研究结果表明：利用蜗杆砂轮磨削面齿轮齿面的关系模型可分析加工过程中面齿轮齿面对应的蜗杆砂轮工作曲面位置，为通过修整蜗杆砂轮对面齿轮齿面制造误差进行补偿修正提供技术基础。
关键词：面齿轮；蜗杆砂轮；接触特性；磨齿加工；关系模型
中图分类号：TH132 文献标志码：A 文章编号：1672-7207(2017)01-0099-07
Relationship between surfaces on worm wheel and on face-gear
TANG Jinyuan, ZHOU Heng
(State Key Laboratory of High Performance Complex Manufacturing,
School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: The principle and method of worm wheel grinding face-gear were researched. The shaper was used as an intermediate surface. Through calculating contact lines among face-gear and shaper, worm wheel and shaper, the contact points between worm wheel and face-gear were calculated in different processing positions. The relationship between the surfaces of worm wheel and face-gear was modeled. The process of grinding face-gear with worm wheel was simulated and verified. The results show that the area on the surface of face-gear which is related to the surface of worm wheel can be analyzed based on the relationship between the surfaces of face-gear and worm wheel modeled in this paper during the grinding process. And also these results can provide technical basis for compensating manufacturing error.
Key words: face-gear; worm wheel; contact characteristics; grinding gear; relationship model
面齿轮传动是一种圆柱齿轮与圆锥齿轮啮合的齿轮传动，由于其在分扭-汇扭传动过程中具有独特的优势，目前是齿轮传动研究的热点[1]。实现面齿轮高精度磨齿加工是面齿轮应用于高速重载领域的前提。在国外，LITVIN等[2-5]对面齿轮传动理论和面齿轮加工技术进行了大量研究，提出采用蜗杆砂轮磨削加工面齿轮的方法，研究了蜗杆的成型原理、齿面方程及根切规律，并研制了面齿轮五轴磨床[6-7]。在国内，TANG等[8-9]研究了利用现有机床采用盘形砂轮磨削的方法对面齿轮进行精加工以及应用插铣的方式高效地对面齿轮进行粗加工；LIU等[10]基于齿轮啮合原理分析了非圆面齿轮的成形过程；CHEN等[11-12]针对面齿轮动力学特性进行了研究；唐进元等[13]针对面齿轮齿距偏差的三坐标测量方法进行了研究；高金忠等[14]研究了磨削面齿轮用基蜗杆的齿面方程，设计参数对蜗杆砂轮根切的影响规律和蜗杆砂轮的修整方法；王延忠等[15]研究了面齿轮滚刀基本蜗杆的设计方法；赵宁等[16]提出采用球形滚刀实现面齿轮滚切加工并分析了该方法的理论加工误差；何国旗等[17]比较了插齿和磨齿加工面齿轮的齿面误差，认为二者在理论齿面上就存在误差。上述研究均没有具体地分析蜗杆砂轮在磨削面齿轮时的齿面对应关系。由于蜗杆砂轮存在奇异性问题，而奇异性会限制蜗杆砂轮产形的转角，在有效转角范围内能否将整个面齿轮齿面完整覆盖加工尚没有进行定量分析。为此，本文作者以产形插齿刀作为中间曲面，在统一坐标系下以微分几何和啮合原理为基础建立产形插齿刀包络面齿轮和蜗杆砂轮的数学模型。通过计算加工过程中产形插齿刀和面齿轮、产形插齿刀和蜗杆砂轮的接触线轨迹的交点，得到蜗杆砂轮和面齿轮的接触点。计算蜗杆砂轮在不同进给位置时可以磨削到面齿轮齿面的位置点，通过判断在有效转角范围内，蜗杆和面齿轮的交点能否覆盖面齿轮整个齿廓来判断是否可以完整加工整个齿面。最后运用数控加工软件VERICUT中仿真验证理论推导过程的正确性。
1 蜗杆砂轮加工面齿轮的产形原理
蜗杆砂轮连续展成磨削加工面齿轮的加工原理如图1所示。当蜗杆砂轮磨削面齿轮时，一方面，蜗杆砂轮与面齿轮作展成运动，以形成面齿轮的齿高齿廓；另一方面，蜗杆砂轮沿着面齿轮的齿向进行进给运动，以形成面齿轮的齿长齿廓。蜗杆砂轮磨削面齿轮时，范成运动和进给运动同时发生。
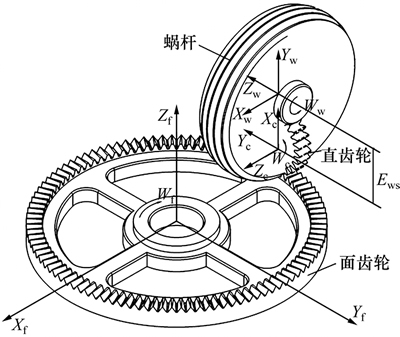
图1 蜗杆磨削面齿轮原理图
Fig. 1 Illustration of grinding face-gear with worm
图2所示为蜗杆砂轮、产形插齿刀和面齿轮相互啮合产形时的坐标系。图2中：Os0为与刀具支架固联的固定坐标系；Os为固联在刀具齿轮上的动坐标系；Ow0为建立在蜗杆砂轮支架上的固定坐标系；Ow为固联在蜗杆砂轮上的动坐标系；O20为与面齿轮支架固联的固定坐标系；O2为固联在面齿轮上的动坐标系；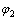
，
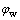和
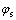分别为面齿轮、蜗杆和刀具齿轮旋转的角度；Ews为蜗杆轴线与面齿轮轴线的最短距离；E2s为蜗杆沿面齿轮径向的进给参数；
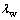为蜗杆偏角。
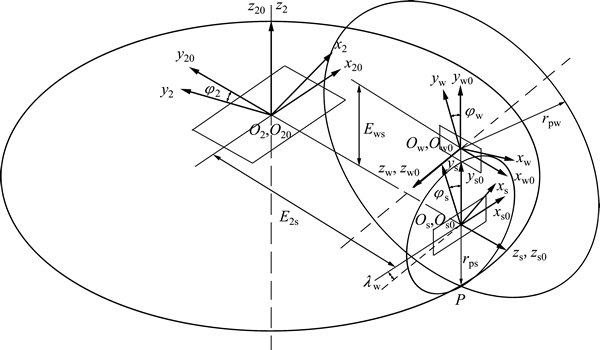
图2 蜗杆砂轮包络坐标系
Fig. 2 Coordinate systems applied for generation of worm surface
1.1 面齿轮的产形过程
面齿轮是由渐开线齿廓的插齿刀包络展成得到的。在插齿加工过程中，插齿刀具转角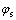和面齿轮转角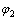满足关系=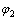
，正交直齿面齿轮齿面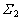
在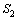
中可以表示为
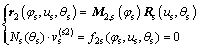(1)
其中：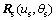
为插齿刀的渐开线齿廓；
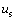和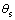
分别为插齿刀轴向参数和渐开线参数；
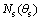为渐开线齿廓法向量；
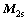为坐标系Os到O2的变换矩阵；
为在Os中齿面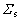
和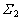的相对速度。求解方程组(1)消去us，正交直齿面齿轮的齿面方程可表示为
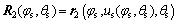(2)
1.2 蜗杆砂轮的产形过程
蜗杆砂轮齿面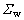
在坐标系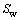
中可表示为
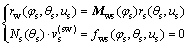(3)
其中：Mws为坐标系Ss到Sw的变换矩阵，齿面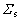和的相对速度表示在Ss中。求解啮合方程fws=0消去us，蜗杆砂轮的齿面方程可表示为
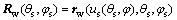(4)
2 面齿轮和插齿刀啮合接触线
2.1 接触轨迹计算
根据插齿刀具与面齿轮的啮合规律，插齿刀具齿面和面齿轮齿面在每一瞬时彼此沿1条线相接触，在加工过程中，所有接触线的集合即为插齿刀具与面齿轮的接触线族。
由面齿轮齿面方程式(2)可知：通过固定转角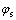，再将参数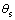离散即可得到1条接触线。面齿轮齿面上的接触线表达式可表示为
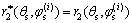(5)
式中：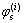
(i=1, 2, …)为被固定的插齿刀具转角参数。选取不同的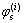可得刀具齿轮与面齿轮的接触轨迹线族。以表1所示设计参数为例。对式(5)求解得插齿刀具与面齿轮在面齿轮齿面上接触线族如图3所示。
2.2 插齿刀产形面齿轮啮合极限转角
由图3可知：插齿刀具在加工过程中与面齿轮左齿面的啮合转角为-21.02°≤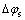
≤10.87°。TANG等[8]指出插齿刀具与面齿轮在啮合过程中2个极限转角分别出现在面齿轮外半径的齿顶位置和内半径的工作齿面与过渡曲线的交点位置，其位置分别如图4中A和B所示(其中：R1和R2分别为面齿轮内和外半径；rsm为刀具齿轮的齿根圆半径)。
表1 面齿轮传动设计参数
Table 1 Design parameters of face-gear transmission
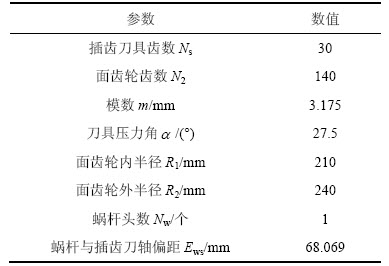
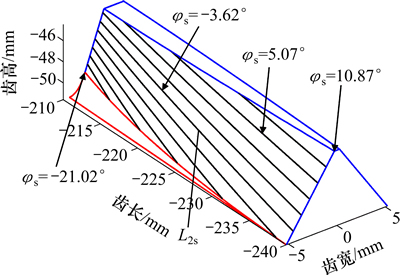
图3 插齿刀与面齿轮的接触线
Fig. 3 Contact lines between shaper and face-gear
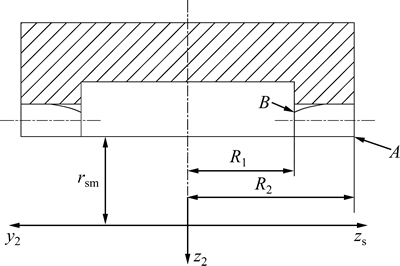
图4 插齿刀具与面齿轮接触极限位置示意图
Fig. 4 Illustration of extreme positions of point A and B in contact lines between shaper and face-gear
外半径处啮合转角极限值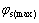
求解公式为
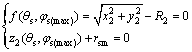(6)
内半径处啮合转角极限值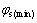
求解公式为
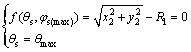(7)
3 蜗杆砂轮和插齿刀啮合接触线
3.1 接触轨迹计算
由蜗杆齿面方程(4)可知：通过固定转角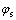，再将参数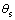离散即可得到1条接触线。面齿轮齿面上的接触线表达式可表示为
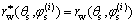(8)
式中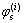：(i=1, 2, …)为被固定的插齿刀具转角参数。选取不同的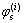可得刀具齿轮与蜗杆砂轮的接触轨迹线族。
以表1所示设计参数为例，对式(8)求解得到插齿刀具与蜗杆砂轮在蜗杆砂轮齿面上接触线族如图5所示。
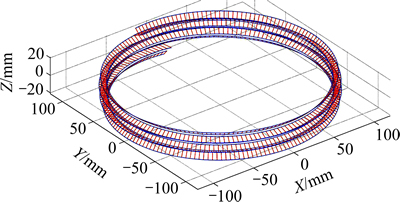
图5 插齿刀与蜗杆砂轮的接触线
Fig. 5 Contact lines between shaper and worm
3.2 插齿刀产形蜗杆砂轮啮合极限转角
由于蜗杆齿面是由刀具齿轮展成包络而成，并不一定是1个正则曲面，曲面上有可能存在奇异点[18]，奇异点会影响蜗杆加工零件时的精度以及蜗杆的使用性能，因此，必须避免蜗杆齿面上的奇异点发生。通过计算可知产形插齿刀齿廓上存在2条奇异接线曲线，如图6所示。
从由图6可知：由于蜗杆奇异性限制在转角-18.3°≤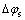≤130.4°内，产形插齿刀会在全齿高范围内与蜗杆齿面接触。但由于在产形过程中，产形插齿刀、面齿轮和蜗杆三者之间两两相互啮合，若需要完整包络面齿轮整个齿面，则需要插齿刀的产形角在-21.02°≤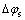≤10.87°范围内。因此，当产形角小于-18.3°时，插齿刀只有部分齿面参与包络，所以，需计算由插齿刀部分齿面展成的蜗杆砂轮能否包络得到完整的面齿轮齿面。
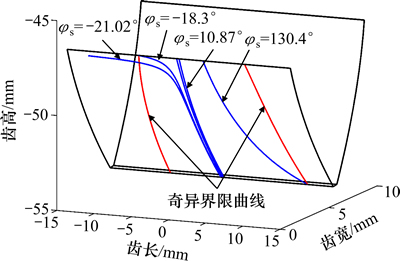
图6 插齿刀与蜗杆砂轮接触极限
Fig. 6 Contact limitation between shaper and worm
4 面齿轮和蜗杆砂轮的磨削接触点
4.1 磨削接触点计算方法
因为在产形过程中产形插齿刀、面齿轮和蜗杆三者之间两两相互啮合，上述计算表明，插齿刀和面齿轮时刻为线接触，插齿刀和蜗杆时刻也为线接触，所以，这2条接触线的交点即为啮合过程中蜗杆和面齿轮的交点。蜗杆和面齿轮的接触点计算步骤如下。
第1步：由图1和图2给定1个蜗杆加工面齿轮时的进给位置E2s。
第2步：由方程(1)得到插齿刀齿面表达式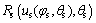
；由方程(3)得到插齿刀齿面表达式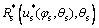
第3步：给定1个转角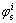
，分别代入第2步得到的插齿刀齿面Rs和
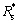。因为固定转角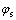离散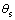时可以得到2条接触线，因此，若下列成立则可求得2条接触线的交点：
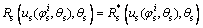(9)
4.2 蜗杆和面齿轮接触点计算示例
以蜗杆砂轮进给到面齿轮齿宽中点处，即以E2s=225 mm为例计算得到面齿轮和蜗杆砂轮的接触点，如图7所示。
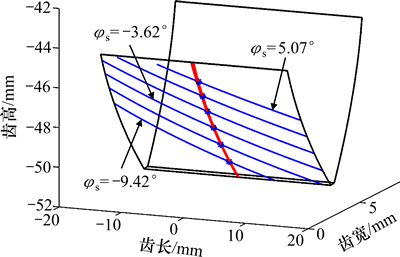
图7 面齿轮和蜗杆砂轮的接触点
Fig. 7 Contact points between worm and face-gear
由图7可见：当假定蜗杆和面齿轮按照啮合运动同时旋转1个角度，然后蜗杆沿着面齿轮径向进给，便可展成1条与图3齿面相对应的接触线。但在实际加工过程中，蜗杆砂轮和面齿轮毛坯按照传动比进行高速旋转运动，同时，蜗杆砂轮沿着面齿轮径向缓慢地进给。为了计算不同进给位置时蜗杆砂轮和面齿轮的接触点，只需在求解接触点的第1步中改变不同的进给位置E2s，将计算所得到的接触点坐标变换到面齿轮坐标系中，如图8所示。由图8可以看出：当蜗杆砂轮沿着面齿轮径向处于不同的进给位置时，蜗杆和面齿轮的啮合运动可以展成得到面齿轮齿面上的1条沟槽，在啮合展成的同时，蜗杆沿着面齿轮径向缓慢进给即可展成得到面齿轮齿面。当蜗杆齿面刚刚出现奇异点，即在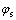=-18.3°处产形插齿刀和面齿轮的接触线。当-21.02°≤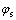＜-18.3°时，由于奇异性的限制， 蜗杆只有在部分齿高范围内可以产形面齿轮。而通过图8所示计算结果可以看到：在有效齿高范围内，蜗杆可以将面齿轮内径底部的齿面完全产形得到。同时，将不同进给位置时求得的接触点坐标变换到蜗杆砂轮坐标系可以发现：在加工过程中，蜗杆砂轮齿面点一一对应于面齿轮齿面点如图9所示。
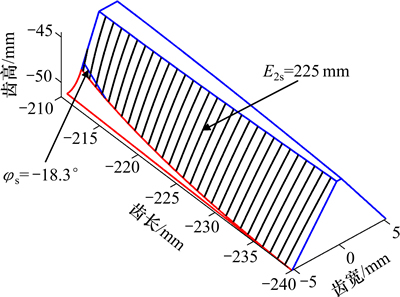
图8 面齿轮上和蜗杆不同进给位置的接触
Fig. 8 Contacts between face-gear and worm on surface of face-gear in different feed locations
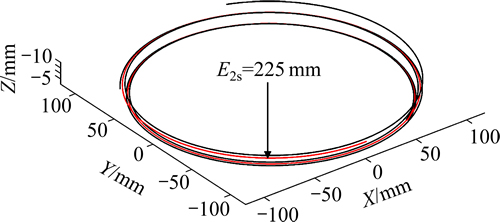
图9 蜗杆上和面齿轮不同进给位置时的接触
Fig. 9 Contacts between face-gear and worm on surface of worm in different feed locations
通过这种一一对应关系，在面齿轮磨削加工出现误差时，通过测量得到的面齿轮齿面误差，从而一一对应去修整蜗杆砂轮的齿面，为误差补偿修整提供技术基础。
5 面齿轮蜗杆砂轮数控加工仿真
由瑞士菜斯豪尔的REISHAUER RZ400数控磨齿机实现本文蜗杆磨削加工面齿轮的运动过程。对其机床结构进行分析建立结构简图，如图10所示。
图10 REISHAUER RZ400机床结构简图
Fig. 10 Machine structural diagram of REISHAUER RZ400
选用表1所示参数，计算得出蜗杆砂轮磨削加工面齿轮的运动参数。首先，根据上述理论分析，在MATLAB软件中计算得到面齿轮和蜗杆砂轮齿面离散点，将离散点导入CATIA软件中构建工件和刀具理论模型，如图11所示。
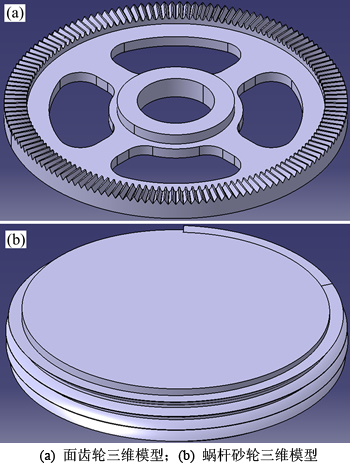
图11 面齿轮和蜗杆砂轮理论三维模型
Fig. 11 Theoretical 3D models of face-gear and worm wheel
利用美国CGTECH公司开发的VERICUT数控仿真软件[19]，通过在软件中构建机床、面齿轮毛坯，并将CATIA建立的工件和蜗杆砂轮刀具理论模型导入VERICUT中构建完整的仿真环境。通过编写数控加工NC程序进行仿真加工，结果如图12所示。由图12可知：面齿轮齿面可由蜗杆砂轮加工得到，这验证了理论分析和数控加工NC程序的正确性。
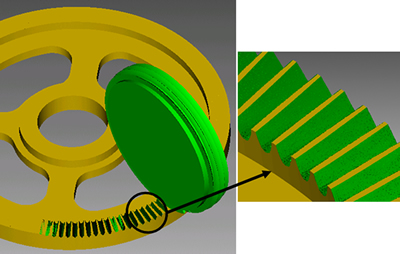
图12 VERICUT中加工仿真结果
Fig. 12 Simulation result of in VERICUT
6 结论
1) 在统一坐标系下研究了面齿轮、产形插齿刀和蜗杆砂轮相互产形原理，以产形插齿刀为中间曲面推导了面齿轮和蜗杆砂轮的包络数学模型。
2) 定量研究了插齿刀产形面齿轮和插齿刀产形蜗杆砂轮的接触轨迹和产形转角范围。
3) 借助产形插齿刀为中间曲面，定量研究了蜗杆砂轮产形面齿轮过程，计算得到了蜗杆砂轮齿面点与面齿轮齿面点一一对应关系，为实际加工过程中针对性地补偿误差修整砂轮提供了理论参考。
4) 在VERICUT数控加工仿真软件中模拟验证了基于蜗杆砂轮磨削加工面齿轮理论推导过程的正确性，对实际加工有一定指导意义。
参考文献：
[1] LITVIN F L. Application of face gear drives in helicopter transmissions[J]. Transaction of the ASME, Journal of Mechanical Design, 1992, 116(3): 672-676.
[2] LITVIN F L, HSIAO C L. Computerized simulation of generation of internal involute gears and their assembly, Transactions of ASME[J]. Journal of Mechanical Design, 1994, 116(3): 683- 689.
[3] LITVIN F L, FUENTES A, ZANZI C, et al. Design, generation,and stress analysis of two versions of geometry of face-gear drives[J]. Mechanism and Machine theory, 2002, 37(10): 1179-1211.
[4] LITVIN F L, IGNACIO G P, FUENTES A, et al. Design and investigation of gear drives with non-circular gears applied for speed variation and generation of functions[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(45/46/47/48): 3783-3802.
[5] LITVIN F L, FUENTES A, ZANZI C, et al. Face gear drive with spur involute pinion: geometry, generation by a worm, stress analysis[J]. Computer Method in Applied Mechanics and Engineering, 2002, 191(25/26): 2785-2813.
[6] LITVIN F L, CHEN Y D, HEATH G F, et al. Apparatus and method for precision grinding face gear: USA, 6146253[P]. 2000-11-14.
[7] TAN J. Tool and method for precision grinding of conical face gear that meshes with a conical involute pinion: USA, 6602115B2[P]. 2003-08-05.
[8] TANG Jinyuan, YIN Feng, CHEN Xingming. The principle of profile modified face-gear grinding based on disk wheel[J]. Mechanism and Machine Theory, 2013, 70(6): 1-15.
[9] YANG Xiaoyu, TANG Jinyuan. Research on manufacturing method of CNC plunge milling for spur face-gear[J]. Journal of Materials Processing Technology, 2014, 214(12): 3013-3019.
[10] LIU Dawei, REN Tingzhi, JIN Xin. Geometrical model and tooth analysis of undulating face gear[J]. Mechanism and Machine Theory, 2015, 86: 140-155.
[11] TANG Jinyuan, HU Zehua, CHEN Siyu, et al. Effects of directional rotation radius and transmission error on the dynamic characteristics of face gear transmission system// Proceedings of the Institution of Mechanical Engineers. Journal of Mechanical Engineering Science, 2014, 228(7): 1108-1118.
[12] CHEN Siyu, TANG Jinyuan, CHEN Weitao, et al. Nonlinear dynamic characteristic of a face gear drive with effect of modification[J]. MECCANICA, 2014, 49(5): 1023-1037.
[13] 唐进元, 李武俊, 张燕, 等. 基于齿距偏差曲面的面齿轮齿距偏差测量[J]. 中南大学学报(自然科学版), 2015, 46(2): 459-464.
TANG Jinyuan, LI Wujun, ZHANG Yan, et al. Measuring and calculating method of face gear pitch deviation based on tooth deviation surface[J]. Journal of Central South University (Science and Technology), 2015, 46(2): 459-464.
[14] 高金忠, 朱如鹏, 李政民卿, 等. 面齿轮滚磨刀具基蜗杆齿廓奇异点研究[J]. 航空动力学报, 2011, 26(10): 2394-2400.
GAO Jinzhong, ZHU Rupeng, LI Zhengminqing. Research on singularities of base worm thread surface for hobbing or grinding face gear[J]. Journal of Aerospace Power, 2011, 26(10): 2394-2400.
[15] 王延忠, 吴灿辉, 葛旭阳, 等. 面齿轮滚刀基本蜗杆的设计方法[J]. 北京航空航天大学学报, 2009, 35(2): 166-169.
WANG Yanzhong, WU Canhui, GE Xuyang, et al. Basal worm-designing method of face-gear hob[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 166-169.
[16] 赵宁, 郭辉, 方宗德, 等. 用球形滚刀滚切面齿轮的理论误差[J]. 航空动力学报, 2009, 24(3): 677-682.
ZHAO Ning, GUO Hui, FANG Zongde, et al. Theory error of cutting face gears with sphericity hob[J]. Journal of Aerospace Power, 2009, 24(3): 677-682.
[17] 何国旗, 严宏志, 何瑛, 等. 面齿轮磨削仿真及齿面误差分析[J]. 中南大学学报(自然科学版), 2014, 45(7): 2193-2200.
HE Guoqi, YAN Hongzhi, HE Ying, et al. Face-gear grinding simulation and tooth surface error analysis[J]. Journal of Central South University (Science and Technology), 2014, 45(7): 2193-2200.
[18] 李特文, 国楷, 叶凌云, 等. 齿轮几何学与应用理论[M]. 上海: 上海科学技术出版社, 2008: 105-140.
LITVIN F L, GUO Kai, YE Lingyun, et al. Gear geometry and applied theory[M]. Shanghai: Shanghai Science and Technology Press, 2008: 105-140.
[19] 杨胜群. VERICUT数控加工仿真技术[M]. 北京: 清华大学出版社, 2010: 1-30.
YANG Shengqun. VERICUT NC machining simulation technology[M]. Beijing: Tsinghua University Press, 2010: 1-30.
(编辑 陈灿华)
收稿日期：2016-01-02；修回日期：2016-03-22
基金项目(Foundation item)：国家自然科学基金资助项目(51535012, U1604255)；湖南省重点研发计划项目(2016JC2001) (Projects(51535012, U1604255) supported by the National Natural Science Foundation of China; Project(2016JC2001) supported by the Key Research and Development Plan of Hunan Province)
通信作者：唐进元，博士，教授，从事复杂曲面零件设计与制造研究；E-mail: jytangcsu@163.com
