
J. Cent. South Univ. (2018) 25: 2654-2663
DOI: https://doi.org/10.1007/s11771-018-3943-0
Adaptive neural network based sliding mode altitude control for a quadrotor UAV
Hadi RAZMI
Department of Electrical Engineering, East Tehran Branch, Islamic Azad University, Tehran, Iran
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Reasons and realities such as being non-linear of dynamical equations, being lightweight and unstable nature of quadrotor, along with internal and external disturbances and parametric uncertainties, have caused that the controller design for these quadrotors is considered the challenging issue of the day. In this work, an adaptive sliding mode controller based on neural network is proposed to control the altitude of a quadrotor. The error and error derivative of the altitude of a quadrotor are the inputs of neural network and altitude sliding surface variable is its output. Neural network estimates the sliding surface variable adaptively according to the conditions of quadrotor and sets the altitude of a quadrotor equal to the desired value. The proposed controller stability has been proven by Lyapunov theory and it is shown that all system states reach to sliding surface and are remaining in it. The superiority of the proposed control method has been proven by comparison and simulation results.
Key words: adaptive sliding mode controller; analog neural network (ANN); altitude control of quadrotor; parametric uncertainty
Cite this article as: Hadi RAZMI. Adaptive neural network based sliding mode altitude control for a quadrotor UAV [J]. Journal of Central South University, 2018, 25(11): 2654–2663. DOI: https://doi.org/10.1007/s11771-018-3943-0.
1 Introduction
Today, unmanned aerial vehicles (UAVs) are an important part of scientific studies in the fields of military and civilian [1–4]. Quadrotor is a vertical take-off and landing (VTOL) aircraft with 6 degrees of freedom (DOF) which has four rotors arranged in a cross shape [5, 6]. This UAV is formed by four rotors which are located in the front, back, left and right, respectively and by changing the rotation speed, each rotor can perform various maneuvers and movements [7, 8]. Lack of size and cost constraints, high maneuverability and low noise, while moving have caused this quadrotor to be at the center of attention and activity of many researchers and scholars around the world [9]. The applications of this device include the inspection and border control, reconnaissance, photography and search operations in dangerous and inaccessible areas [10, 11]. Due to the high sensitivity of this vehicle to the smallest control commands, the design of an appropriate controller to enhance the accuracy of its flight is very important [12]. So far, different control methods to control the position, altitude and attitude of quadrotor have been proposed. In Ref. [13], some of these methods have been reviewed. Sliding mode controller is one of these controllers due to its many advantages and its extended methods have been proposed.
In Ref. [8], effect of the disturbances and parameter uncertainties on the position and attitude tracing of quadrotor unmanned aerial vehicles (UAVs) has been solved by an adaptive radical basis function neural networks (RBFNNs) and double-loop integral sliding mode control (IntSMC). In addition, a robust nonlinear controller based on the backstepping control technique was proposed in Ref. [14].
A continuous sliding mode control for the quad rotor aircraft system has been addressed in Ref. [15] to maximize the efficient performance. In Ref. [16], a framework for the Newton–Euler underactuated dynamic model of a quadrotor has been presented, which induces integral sliding modes and smooth bounded disturbances. To obtain a finite-time position and attitude tracking control of a small quadrotor UAV, a control method based on global fast dynamic terminal sliding mode control (TSMC) was presented in Ref. [17]. In Ref. [18] a synthesis control method of the dynamical model of a small quadrotor unmanned aerial vehicle (UAV) has been presented. The proposed technique is underactuated, highly- coupled and nonlinear. In Ref. [19], a novel adaptive fuzzy gain-scheduling sliding mode control (AFGS-SMC) method with respect to attitude regulation of unmanned quadrotor was proposed. In Ref. [20], a second- order sliding mode control (2-SMC) to design controllers for a small quadrotor unmanned aerial vehicle (UAV) has been presented. In Ref. [21], the position and attitude tracking control for a quadrotor UAV via discrete-time sliding mode control (DSMC) has been addressed. In Refs. [22, 23], a hybrid controller for a six-degree of freedom (6 DOF) coaxial trirotor helicopter control was proposed. In the proposed model, the coupling of the interval type-2 fuzzy logic control and sliding mode control technique was used. In Ref. [24], the novel robust terminal sliding mode control (NRTSMC) and under-actuated system sliding mode control (USSMC) methods was presented for a small quad rotor unmanned helicopter (QRUH).
Parametric uncertainties compensation is one of the important advantages of sliding mode controller of which advantage is not considered in many papers. One of the parameters changed by factors such as battery consumption, wind blow or the collision of an object to quadrotor is quadrotor mass. Giving the uncertainty in the mass parameter may cause steady state error (SSE) in altitude control of quadrotor. As shown in this paper, considering the uncertainty in quadrotor mass parameter will make the steady state error in altitude control results of the proposed controller in Ref. [20]. So, the main purpose of this paper is to improve the performance of altitude control of quadrotor in the presence of parametric uncertainties. This work is done by adding an analog neural network (ANN) to proposed controller in Ref. [20]. In fact, neural network, according to error and error derivative, estimates the altitude sliding surface variable adaptively. Then, the output of neural network is used to produce the altitude control signal of quadrotor. Simulation results show that the quadrotor altitude control operations in spite of uncertainty in the mass parameter are performed without steady-state error.
The aim of this study is to design an adaptive sliding mode controller based on neural network to control the altitude of a quadrotor, to investigate this method robustness in the presence of parametric uncertainties, and to investigate the existence of chattering in control inputs. The main contributions of this paper are: define a non-linear sliding surface to improve the results of quadrotor altitude control; Use a neural network along with sliding mode controller to control the quadrotor altitude without steady state error in the presence of parametric and non-parametric uncertainties; remove the chattering in control inputs. This paper consists of the following sections: The second section is dedicated to a dynamic model of quadrotor. Design of quadrotor position and attitude controller is expressed in the third section. In the fourth section, adaptive sliding mode controller based on neural network to control the quadrotor altitude is presented. The simulation results of the proposed method are compared with a similar method in the fifth section. Sixth section is devoted to conclusions.
2 Dynamic modeling of quadrotor
In Figure 1, quadrotor schematic is shown along with the details. To obtain the quadrotor dynamic equations, both of the earth-frame E(Oexeyez) and body-frame B(Oxyz) are required. In this figure the following definitions are established: ms is the total mass of quadrotor; g is the acceleration of gravity; l is the distance from the center of each rotor to the center of the gravity of quadrotor; Fi (i=1, 2, 3, 4) is the thrust generated by the rotor i; [x, y, z]T is the position vector of the center of the gravity of quadrotor in earth-frame; [f, θ, ψ]T is the orientation angle vector of quadrotor in body-frame. It should be noted that the Euler angles f, θ and ψ called roll, pitch and yaw angles,respectively, have (–π/2 By applying the Newton–Euler approach, a set of dynamic equations of a quadrotor in earth-frame can be obtained as Eq. (1) [17, 18, 20, 25].
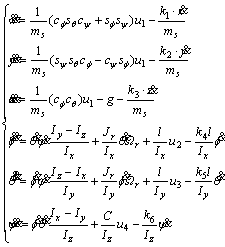 (1)
(1)
where Ix, Iy and Iz are the mass moments of inertia in the x, y and z axes, respectively; Ωr=–Ω1+Ω2–Ω3+Ω4 is the overall residual rotor angular velocity; Ωi (i=1, 2, 3, 4) is the angular speed of the propeller i; Jr is the inertia of the propeller; C is the force to moment scaling factor; And k1 to k6 are positive constant numbers that are called the drag coefficients.
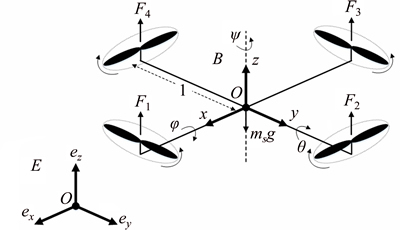
Figure 1 Quadrotor schematic
In Eq. (1), the symbol of c instead of cos and s instead of sin have been used. For example, cψ represents cos(ψ).
Control inputs of u1–u4 are calculated by Eq. (2) [17, 18, 20].
 (2)
(2)
where u1 represents the total thrust on the body in the z-axis; u2, u3 and u4 are the roll, pitch and yawing torques, respectively. Also, k>0 and b>0 are two constant parameters of which values depend on the density of air, the radius of the propeller, the number of blades, the geometry and the lift and drag coefficients of the blade [20].
In extracting these equations, it is assumed that the angular velocity of the quadrotor in body-flame and earth-flame when the quadrotor is hovering in the air, are the same; quadrotor structure is rigid and symmetric; the center of gravity and the origin of the body-frame is one and the axes of the body-frame are coincident to quadrotor inertia axes [22, 23].
3 Sliding mode controller design
In this paper, the second-order sliding mode controller is used to control the position and attitude of a quadrotor. Dynamic model of quadrotor is divided into two sub-systems of fully actuated and under actuated. In fully actuated sub-system, the controller must be designed in a way of which state variables of z and ψ can track the desired paths of zd and ψd. Due to the structure of quadrotor its rotors are considered rigid and symmetric, so Ix=Iy. The dynamic equations required for this sub-system are rewritten by Eqs. (3) and (4).
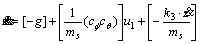 (3)
(3)
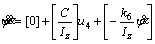 (4)
(4)
Differential equations of a second-order single input single output (SISO) non-linear system can be shown by Eq. (5).
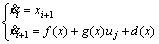 (5)
(5)
In Eq. (5), x=[x1, …, xi, xi+1, …, xn]T is system state variables vector; uj is the jth control input; f(x) and g(x) are non-linear, real and known functions and 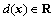 is the bounded external disturbance.
is the bounded external disturbance.
By defining ei=xi–xid as the ith error signal, where xid is the desired path for state variable xi, sliding surface si is expressed by Eq. (6).
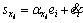 (6)
(6)
By considering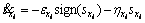 and inserting it into the equation
and inserting it into the equation 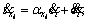 Eq. (7) is obtained.
Eq. (7) is obtained.
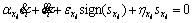 (7)
(7)
By substituting equations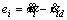 and
and 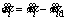 in Eq. (7), Eq. (8) is obtained.
in Eq. (7), Eq. (8) is obtained.
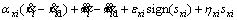 (8)
(8)
So, by using Eqs. (5) and (8), control input uj will be achieved as Eq. (9).
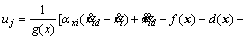
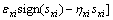 (9)
(9)
It should be noted that d(x) in Eq. (9) is composed of sentences that detailed information is not available. So, in defining uj, d(x) as not modeled dynamic can be ignored. According to Eq. (5), in Eqs. (3) and (4), we have:
In Eq. (3), i=1, j=1, x1=z, 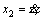 f(x)=–g,
f(x)=–g, 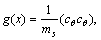 and
and 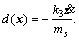
In Eq. (4), i=3, j=4, x3=ψ, 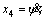 f(x)=0,
f(x)=0, 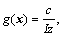 and
and 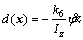
According to Eq. (6), in this subsystem, the sliding surfaces sz and sψ are defined by Eqs. (10) and (11), respectively.
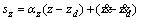 (10)
(10)
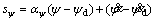 (11)
(11)
And in accordance with Eq. (9), control inputs u1 and u4 are expressed by Eqs. (12) and (13), respectively.
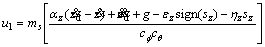 (12)
(12)
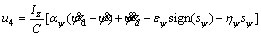 (13)
(13)
In under actuated sub-system, the controller must be designed so that the state variables [x, θ] and [y, f] can track the desirable paths [xd, θd] and [yd, fd], respectively. Dynamical equations required for this subsystem are rewritten by Eqs. (14) and (15).
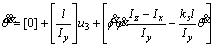 (14)
(14)
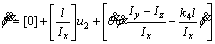 (15)
(15)
According to Eq. (5), Eqs. (14) and (15), we have:
In Eq. (14), i=7, j=3, x7=θ, 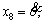 f(x)=0,
f(x)=0, 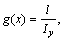 and
and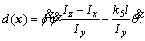
In Eq. (15), i=11, j=2, x11=f, 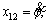 f(x)=0,
f(x)=0, 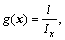 and
and 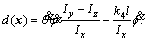
Due to the fact that in under actuated sub-system, x and θ or y and f are controlled simultaneously, the four remaining state variables are defined as x5=x, 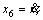 x9=y, and
x9=y, and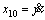 Unlike fully actuated sub-system, in this subsystem any sliding surface is linear combination of error of four state variables. In Eqs. (16) to (19), sliding surfaces sθ and sf with their first-order derivatives are introduced [18].
Unlike fully actuated sub-system, in this subsystem any sliding surface is linear combination of error of four state variables. In Eqs. (16) to (19), sliding surfaces sθ and sf with their first-order derivatives are introduced [18].
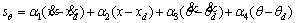 (16)
(16)
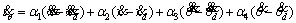 (17)
(17)
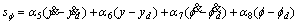 (18)
(18)
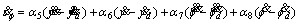 (19)
(19)
By considering 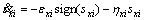 (i=7, 11), control inputs u3 and u2 with ignoring d(x) are obtained as Eqs. (20) and (21), respectively.
(i=7, 11), control inputs u3 and u2 with ignoring d(x) are obtained as Eqs. (20) and (21), respectively.
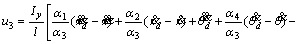
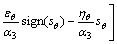 (20)
(20)
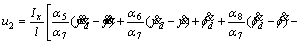
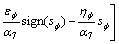 (21)
(21)
To prove stability of the system, positive definite Lyapunov function in accordance with Eq. (22) is considered.
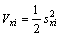 (i=1, 3, 7, 11) (22)
(i=1, 3, 7, 11) (22)
Eq. (23) shows the derivative of this Lyapunov function.
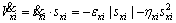 (23)
(23)
If εxi and ηxi are selected real positive,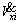 will always be negative definite and therefore according to the Lyapunov theorem, system will be stable.
will always be negative definite and therefore according to the Lyapunov theorem, system will be stable.
Citing Ref. [20] and by applying Hurwitz stability theorem on linearized under actuated sub- system, switching surface coefficients sθ and sf are obtained as follows:
α3=1,α4=6α3,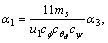
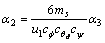 ,
,
α7=1, α8=6α7, 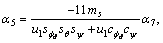 and
and 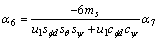 .
.
Furthermore, it is clear that for becoming sliding surface to zero, error and its derivative in steady-state, in fully actuated sub-system, αxi coefficient in Eq. (6) should be chosen positive. In Ref. [20], this coefficient is assumed equal to one. In this paper it will be shown that using this constant number to control the quadrotor altitude when there is uncertainty in ms parameter, the desired results will not be obtained. Thus, adaptive selection of this coefficient in the presence of uncertainty in parameter ms is the main idea of this paper.
4 Adaptive altitude control system of quadrotor
Nowadays, artificial neural networks are known as reliable methods to solve complex nonlinear control problems [26, 27]. Artificial neural networks for control applications are divided into two types of digital and analog neural networks. Digital neural networks with discrete learning algorithms are plurality presented due to advantages such as predictable accuracy, high noise-immunity, and availability of well-established tools for digital design and ease of interfacing with other digital systems. On the other hand, Analog neural networks with continuously learning algorithms have advantages such as high speed, small size, low cost, low power consumption and straightforward interfacing with the outside word that is analog by nature and also ability to build by electronic elements or chips [26]. Control systems have to work in real-time and therefore they need to speed in calculations. Today, most advances in robotics and automation, due to the large size, high cost and power consumption are impractical in control systems. To solve the above problems, in this paper, an Analog neural network is combined with sliding mode controller. The mentioned combination, in addition to the advantages of sliding mode controller has advantages such as analog neural networks ability in continuous online learning, adaptability and tackling nonlinearity dynamic. If the system under the control is highly non-linear and has parametric and non-parametric uncertainties, definition of a linear sliding surface by using the neural network may not produce the desired control result. So, in this paper, a non-linear sliding surface is configured by using the neural network and this method will improve the control result.
Altitude control algorithm structure of quadrotor based on Analog neural networks is shown in Figure 2. Quadrotor altitude can be controlled by adjusting the state variable z. The purpose of control is the definition of an adaptive sliding surface based on neural network so that tracking error ez=z–zd becomes zero.
Analog neural network structure has been shown in Figure 3. In this figure αz is the adaptable proportional coefficient. The tracking error ez and its derivative 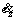 are neural network inputs. Sliding surface sz is neural network output and is obtained by Eq. (24).
are neural network inputs. Sliding surface sz is neural network output and is obtained by Eq. (24).
sz=f(h) (24)
where h is input of sigmoid function f(·) and is expressed by Eq.(25).
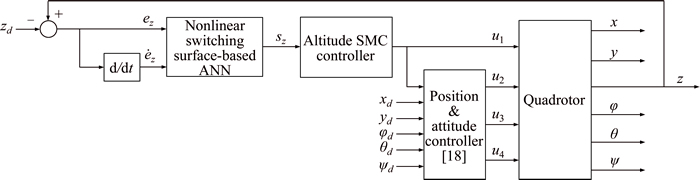
Figure 2 Altitude control algorithm structure of quadrotor
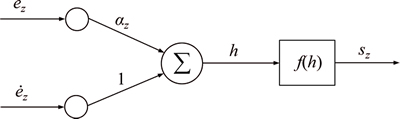
Figure 3 Block of non-linear sliding surface calculating based on neural network
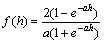 (25)
(25)
where a is a parameter that specifies the shape of sigmoid function. Input signal of sigmoid function in output layer is:
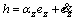 (26)
(26)
Neural network with the conventional back propagation algorithm is trained to minimize the tracking error ez, defined by Eq. (27).
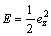 (27)
(27)
To adjust the proportional coefficient αz, gradient descent method [26] is used, which leads to the following equation:
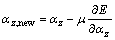 (28)
(28)
where μ is the learning rate which determines the convergence speed of neural network, and αz,new is the new value of proportional coefficient αz. By using the chain rule, 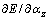 is obtained in accordance with Eq. (29).
is obtained in accordance with Eq. (29).
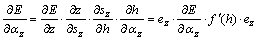 (29)
(29)
By replacing 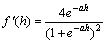 and assuming
and assuming 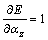 [26], Eq. (30) will be obtained.
[26], Eq. (30) will be obtained.
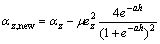 (30)
(30)
In the fifth section, the effectiveness of adaptive sliding mode controller based on neural network to control the quadrotor altitude in the presence of uncertainty in the mass parameter of this quadrotor will be shown by simulation and comparison results.
5 Simulation results
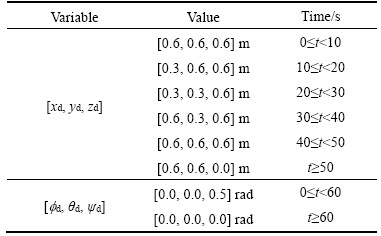
In this section, the effectiveness of the proposed sliding mode controller to control quadrotor altitude is evaluated by simulation results. In controller design, d(x) term as not modeled dynamic part is neglected to consider non- parametric uncertainty. In addition, parametric uncertainty is considered 10% of error rate in mass parameter value of quadrotor. Thus, the robustness of the proposed controller in the presence of these parametric and nonparametric uncertainties is discussed in all results of this section. All simulations in this section have been conducted in the MATLAB/Simulink software. In Table 1, the parameters values of quadrotor model are shown. Also, values of the proposed controller parameters are summarized in Table 2. Obviously, if taking into account other parameters for controller and quadrotor model, the results will be changed. Square path tracking presented in Table 3 is considered to test the proposed controller. In all simulations of this section, the initial state values are assumed to be zero.
In Figure 4, the results of proposed controller in this paper and proposed controller in Ref. [18],are compared in tracking of the desired variables x, y and z. As can be seen in this figure, the existence of uncertainty in mass parameter of quadrotor will not change the tracking results, the variables x and y of controller proposed in Ref. [20]. But the variable z by this controller is tracked with steady-state error.However, tracking of the variable z by the controller proposed in this paper has been conducted without steady-state error.
Table 1 Parameters values of quadrotor model
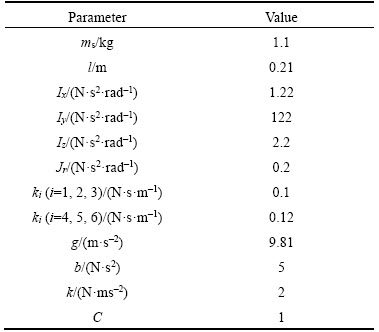
Table 2 Values of controller parameters

Table 3 Desirable positions and attitude in square path
In Figure 5, control inputs u1 to u4 of the proposed controller are shown. As can be seen in these figures, the use of sign function creates chattering in control inputs u2 to u4, which is undesirable. It should be noted that to eliminate or reduce the chattering in these control inputs, saturation function can be used instead of sign function. In order to compare the previous state, control inputs u1 to u4 while using saturation function are shown in this figure.
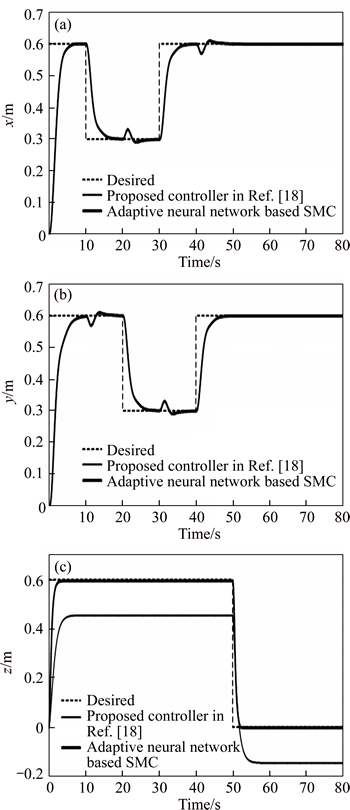
Figure 4 Comparing the results of tracking variables x, y and z
In Figure 6, the obtained results of two controllers in tracking the desired square path are compared with each other. In this figure, the superiority of controller proposed in this paper, compared with controller proposed in Ref. [20] to control the quadrotor altitude in the presence of parametric uncertainties, is clearly observed.
The application of the proposed controller in altitude control purposes is studied and tested in other desirable paths. In all of them like square path the simulation results indicate high accuracy and robustness of controller exposed to parametric and non-parametric uncertainties.
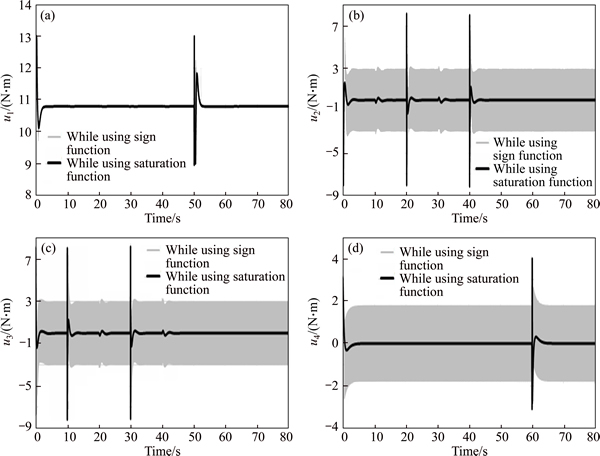
Figure 5 Control inputs u1 to u4
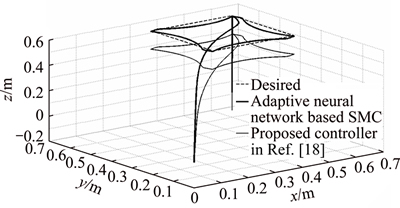
Figure 6 Quadrotor path
6 Conclusions
Design of altitude controller for quadrotor due to reasons such as being non-linear of dynamical equations, parametric and nonparametric uncertainties, being lightweight, unstable nature and unexpected winds, is considered the challenging issues of the day. In this paper, after explanation the dynamic equations of quadrotor, the second-order sliding mode controller was used to control the position and attitudes of this quadrotor. To achieve optimal performance quadrotor altitude control, a very simple Analog neural network is used to estimate the altitude sliding surface variable adaptively. The use of this neural network leads to perform tracking the desirable altitude for this quadrotor without steady-state error in despite of the uncertainty in the mass parameter of quadrotor. Lyapunov theory is used to prove the stability of the proposed controller and it was shown that all system states reach to sliding surface and remain in it. The superiority of adaptive sliding mode controller based on neural network compared with controller proposed in reference is shown by simulation results of tracking a desired square path. Also, the chattering in control input u1 is removed by using neural network. To remove the chattering in other control inputs, using saturation function instead of sign function is proposed. Adaptability of this methodology to control the quadrotor altitude in the presence of parametric and non-parametric uncertainties is its main feature. In this paper, quadrotor altitude control issue was just noticed. A similar work can be done to improve the control operation of position and attitude of a quadrotor. The research work is continuing to implement this proposal.
Acknowledgments
The author is thankful to authorities of East Tehran Branch, Islamic Azad University, Tehran, Iran, for providing support and necessary facilities.
References
[1] ZHU X, ZHANG X X, QU Y H. Three-dimensional formation keeping of multi-UAV based on consensus [J]. Journal of Central South University, 2017, 24(6): 1387– 1395.
[2] WANG B, HOU Z X, LU Y F, ZHU X F. Hover performance estimation and validation of battery powered vertical takeoff and landing aircraft [J]. Journal of Central South University, 2016, 23(10): 2595–2603.
[3] LIN C, XIAO J, LI D, WENG Q. Radon transform-based indoor localization control for quadrotor [J]. Optik- International Journal for Light and Electron Optics, 2016, 127(19): 8056–8064.
[4] CHEN Y M, HE Y L, ZHOU M F. Decentralized PID neural network control for a quadrotor helicopter subjected to wind disturbance [J]. Journal of Central South University, 2015, 22(1): 168–179.
[5] SONG Y, XIAN B, ZHANG Y, JIANG X, ZHANG X. Towards autonomous control of quadrotor unmanned aerial vehicles in a GPS-denied urban area via laser ranger finder [J]. Optik-International Journal for Light and Electron Optics, 2015, 126(23): 3877–3882.
[6] MIRZAEI M, EGHTESAD M, ALISHAHI M M. A new robust fuzzy method for unmanned flying vehicle control [J]. Journal of Central South University, 2015, 22(6): 2166–2182.
[7] ROZA A, MAGGIORE M. A class of position controllers for underactuated VTOL vehicles [J]. IEEE Transactions on Automatic Control, 2014, 59(9): 2580–2585.
[8] LI S, WANG Y, TAN J, ZHENG Y. Adaptive RBFNNs/integral sliding mode control for a quadrotor aircraft [J]. Neurocomputing, 2016, 216: 126–134.
[9] P REZ-ALCOCER R, MORENO-VALENZUELA J, MIRANDA-COLORADO R. A robust approach for trajectory tracking control of a quadrotor with experimental validation [J]. ISA Transactions, 2016, 65: 262–274.
REZ-ALCOCER R, MORENO-VALENZUELA J, MIRANDA-COLORADO R. A robust approach for trajectory tracking control of a quadrotor with experimental validation [J]. ISA Transactions, 2016, 65: 262–274.
[10] JABBARI ASL H, YOON J. Adaptive vision-based control of an unmanned aerial vehicle without linear velocity measurements [J]. ISA Transactions, 2016, 65: 296–306.
[11] CHANG K, XIA Y, HUANG K, MA D. Obstacle avoidance and active disturbance rejection control for a quadrotor [J]. Neurocomputing, 2016, 190: 60–69.
[12] SALAZAR-CRUZ S, KENDOUL F, LOZANO R, FANTONI I. Real-time stabilization of a small three-rotor aircraft [J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 783–794.
[13] ZULU A, JOHN S. A review of control algorithms for autonomous quadrotors [J]. Open Journal of Applied Sciences, 2014, 4: 547–556.
[14] CHEN F, JIANG R, ZHANG K, JIANG B, TAO G. Robust backstepping sliding mode control and observer-based fault estimation for a quadrotor UAV [J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 5044–5056.
[15] GONZ LEZ I, SALAZAR S, LOZANO R. Chattering-free sliding mode altitude control for a quad-rotor aircraft: Real-time application [J]. Journal of Intelligent & Robotic Systems, 2014, 73(1): 137–155.
LEZ I, SALAZAR S, LOZANO R. Chattering-free sliding mode altitude control for a quad-rotor aircraft: Real-time application [J]. Journal of Intelligent & Robotic Systems, 2014, 73(1): 137–155.
[16] RAMIREZ-RODRIGUEZ H, PARRA-VEGA V, SANCHEZ-ORTA A, GARCIA-SALAZAR O. Robust backstepping control based on integral sliding modes for tracking of quadrotors [J]. Journal of Intelligent & Robotic Systems, 2014, 73(1): 51–66.
[17] XIONG J J, ZHANG G B. Global fast dynamic terminal sliding mode control for a quadrotor UAV [J]. ISA Transactions, 2016, 66: 233–240.
[18] ZHENG E H, XIONG J J, LUO J L. Second order sliding mode control for a quadrotor UAV [J]. ISA Transactions, 2014, 53(4): 1350–1356.
[19] YANG Y, YAN Y. Attitude regulation for unmanned quadrotors using adaptive fuzzy gain-scheduling sliding mode control [J]. Aerospace Science and Technology, 2016, 54: 208–217.
[20] XIONG J J, ZHENG E H. Position and attitude tracking control for a quadrotor UAV [J]. ISA Transactions, 2014, 53(3): 725–731.
[21] XIONG J J, ZHANG G. Discrete-time sliding mode control for a quadrotor UAV [J]. Optik-International Journal for Light and Electron Optics, 2016, 127(8): 3718–3722.
[22] ZEGHLACHE S, KARA K, SAIGAA D. Fault tolerant control based on interval type-2 fuzzy sliding mode controller for coaxial trirotor aircraft [J]. ISA Transactions, 2015, 59: 215–231.
[23] ZEGHLACHE S, SAIGAA D, KARA K. Fault tolerant control based on neural network interval type-2 fuzzy sliding mode controller for octorotor UAV [J]. Frontiers of Computer Science, 2016, 10(4): 657–672.
[24] ZHENG E, XIONG J. Quad-rotor unmanned helicopter control via novel robust terminal sliding mode controller and under-actuated system sliding mode controller [J]. Optik-International Journal for Light and Electron Optics, 2014, 125(12): 2817–2825.
[25] XIONG J J, ZHENG E H. Optimal Kalman filter for state estimation of a quadrotor UAV [J]. Optik-International Journal for Light and Electron Optics, 2015, 126(21): 2862–2868.
[26] YE J. Adaptive control of nonlinear PID-based analog neural networks for a nonholonomic mobile robot [J]. Neurocomputing, 2008, 71(7): 1561–1565.
[27] WU B, HAN S, XIAO J, HU X, FAN J. Error compensation based on BP neural network for airborne laser ranging [J]. Optik-International Journal for Light and Electron Optics, 2016, 127(8): 4083–4088.
(Edited by YANG Hua)
中文导读
基于自适应神经网络的四转子无人机滑模高度控制
摘要:由于动力学方程的非线性、四转子的轻量化和不稳定性等原因和现实情况,加上内、外扰动和参数不确定性等因素,使得四转子控制器的设计成为当今研究的热点。本文提出一种基于神经网络的自适应滑模控制器来控制四转子的高度。四转子高度的误差和误差导数是神经网络的输入,高度滑动面变量是输出。神经网络根据四转子的条件自适应地估计滑动面变量,并将四转子的高度设为期望值。用李雅普诺夫理论证明了该控制器的稳定性,证明了系统的所有状态都达到了滑动面,并保持在滑动面内。通过对比和仿真,验证了所提出的控制方法的优点。
关键词:自适应滑模控制器;模拟神经网络;四转子高度控制;参数不确定性
Received date: 2017-04-25; Accepted date: 2017-11-09
Corresponding author: Hadi RAZMI, PhD, Assistant Professor; Tel: +98-21-33594950; Fax: +98-21-33584011; E-mail: razmi.hadi@ gmail.com; ORCID: 0000-0003-3528-0164